GSEB Solutions Class 12 Statistics Part 1 Chapter 2 रैखिक सह-सम्बन्ध Ex 2

Gujarat Board Statistics Class 12 GSEB Solutions Part 1 Chapter 2 रैखिक सह-सम्बन्ध 2 Textbook Exercise Questions and Answers.

Gujarat Board Textbook Solutions Class 12 Statistics Part 1 Chapter 2 रैखिक सह-सम्बन्ध 2

विभाग – A

निम्न दिये गये विकल्प के लिए सही विकल्प चयन करके लिखिए ।

प्रश्न 1.
सह-सम्बन्ध के संदर्भ में जिस आकृति में युग्मयुक्त बिन्दुओं (x, y) दर्शाया जाय उस आकृति को आप क्या कहोगे ?
(a) स्तंभाकृति
(b) वृत आकृति
(c) विकीर्ण आकृति
(d) आवृति वक्र
उत्तर :
(c) विकीर्ण आकृति

प्रश्न 2.
यदि x और y के बीच निम्नानुसार विकीर्ण आकृति प्राप्त हो, तो दो चल के बीच कैसा सह-सम्बन्ध होता है ?

(a) संपूर्ण धनात्मक सह-सम्बन्ध
(b) आंशिक धनात्मक सह-सम्बन्ध
(c) संपूर्ण ऋणात्मक सह-सम्बन्ध
(d) आंशिक ऋणात्मक सह-सम्बन्ध
उत्तर :
(a) संपूर्ण धनात्मक सह-सम्बन्ध

प्रश्न 3.
यदि x और y के बीच निम्नानुसार विकीर्ण आकृति प्राप्त हो, तो दो चल के बीच कैसा सह-सम्बन्ध होता है ?

(a) संपूर्ण धनात्मक सह-सम्बन्ध
(b) आंशिक धनात्मक सह-सम्बन्ध
(c) संपूर्ण ऋणात्मक सह-सम्बन्ध
(d) आंशिक ऋणात्मक सह-सम्बन्ध
उत्तर :
(d) आंशिक ऋणात्मक सह-सम्बन्ध

प्रश्न 4.
विकीर्ण आकृति में सभी बिंदु एक ही सुरेखा पर आये हुए हो, तो r का मूल्य कितना होगा ?
(a) r = 0
(b) 1 अथवा -1
(c) r = 0.5
(d) -0.5
उत्तर :
(b) 1 अथवा -1

प्रश्न 5.
सह-संबंध गुणांक r का विस्तार कितना होगा ?
(a) -1 < r <1
(b) 0 से 1
(c) -1 ≤ r ≤ 1
(d) -1 से 0
उत्तर :
(c) -1 ≤ r ≤ 1

प्रश्न 6.
यदि चल ‘वजन’ की इकाई किग्रा और चल ऊँचाई’ की इकाई सेमी. हो, तो उसके बीच के सह-सम्बन्ध की इकाई के बारे में क्या कहा जायेगा ?
(a) किग्रा
(b) सेमी
(c) किमी
(d) इकाई से मुक्त है ।
उत्तर :
(d) इकाई से मुक्त है ।

प्रश्न 7.
यदि दो चल के बीच अचल प्रमाण में एकदूसरे से विरुद्ध दिशा में परिवर्तन हो, तो दो चल के बीच किस प्रकार का सह सम्बन्ध होगा ?
(a) आंशिक धनात्मक सह-सम्बन्ध
(b) संपूर्ण ऋणात्मक सह-सम्बन्ध
(c) संपूर्ण धनात्मक सह-सम्बन्ध
(d) आंशिक ऋणात्मक सह-सम्बन्ध
उत्तर :
(b) संपूर्ण ऋणात्मक सह-सम्बन्ध

प्रश्न 8.
कार्ल पियर्सन के सह-सम्बन्ध की गणना के सूत्र में अंश क्या दर्शाता है ?
(a) x और y के विचरणों का गुणाकार
(b) x और y का सहविचरण
(c) x का विचरण
(d) y का विचरण
उत्तर :
(b) x और y का सहविचरण

प्रश्न 9.
निम्न में से r का कौन-सा मूल्य संभव नहीं है ?
(a) 0.99
(b) -1.07
(c) -0.85
(d) 0
उत्तर :
(b) -1.07

प्रश्न 10.
यदि u = \(\frac{\mathrm{x}-\mathrm{A}}{\mathrm{cx}}\) और v = \(\frac{\mathrm{y}-\mathrm{B}}{\mathrm{cy}}\), Cx > 0, Cy > 0 हो, तो निम्न में से कौन-सा विधान सत्य है ?
(a) r(x, y) ≠ r(u, v)
(b) r(x, y) > r(u, v)
(c) r(x, y) = r(u, v)
(d) r(x, y) < r(u, v)
उत्तर :
(c) r(x, y) = r(u, v)

प्रश्न 11.
यदि r(x, y) = 0.7 हो, तो r(x + 0.2, y + 0.2) का मूल्य कितना होगा ?
(a) 0.7
(b) 0.9
(c) 1.1
(d) -0.7
उत्तर :
(a) 0.7

प्रश्न 12.
यदि r(-x, y) = -0.5 हो, तो r(x, -y) का मूल्य कितना होगा ?
(a) 0.5
(b) -0.5
(c) 1
(d) 0
उत्तर :
(b) -0.5

प्रश्न 13.
यदि Σd² = 0 हो, तो कोटि सहसम्बन्ध गुणांक का मूल्य कितना होगा ?
(a) 0
(b) -1
(c) 1
(d) 0.5
उत्तर :
(c) 1

प्रश्न 14.
क्रमांक सहसम्बन्ध की विधि में यदि प्रत्येक अवलोकन के युग्म के लिए प्रचलित संकेत में Rx = Ry हो, तो r का मूल्य कितना होगा ?
(a) 0
(b) -1
(c) 1
(d) 0.1
उत्तर :
(c) 1

प्रश्न 15.
क्रमांक सहसंबंध की विधि में दो चल के कोटियाँ के अंतर का योग क्या होगा ?
(a) 0
(b) -1
(c) 1
(d) कोई भी वास्तविक संख्या
उत्तर :
(a) 0

प्रश्न 16.
क्रमांक सह-सम्बन्ध की विधि में यदि दो चल की कोटि एकदूसरे से विरूद्ध क्रम में हो, तो r का मूल्य कितना होगा ?
(a) r = 0
(b) r = -1
(c) r = 1
(d) r = 0%
उत्तर :
(b) r = -1

प्रश्न 17.
क्रमांक सह-सम्बन्ध में पुनरावर्तित होते प्रत्येक अवलोकन के लिए प्रचलित संकेत में Σd² में कौन-सा पद जोड़ा जाता है ?
(a) \(\frac{m^2-1}{12}\)
(c) \(\frac{\mathrm{m}^3-\mathrm{m}}{12}\)
(b) \(\frac{6 m^3-m}{12}\)
(d) n(n² – 1)
उत्तर :
(b) \(\frac{6 m^3-m}{12}\)

प्रश्न 18.
जब किसी वस्तु के मूल्य स्थिर हो तब उस वस्तु के बिक्री हुई इकाईयाँ की संख्या और उसमें होती आय के बीच कैसा सह सम्बन्ध होगा ?
(a) संपूर्ण धनात्मक
(b) आंशिक धनात्मक
(c) संपूर्ण ऋणात्मक
(d) आंशिक ऋणात्मक
उत्तर :
(a) संपूर्ण धनात्मक

विभाग – B

निम्न प्रश्नों के एक वाक्य में उत्तर दीजिए ।

प्रश्न 1.
सह-सम्बन्ध की परिभाषा दीजिए ।
उत्तर :
दो सम्बन्धित चरों की कीमत में प्रत्यक्ष या परोक्ष कारणों से एक साथ वृद्धि-कमी हो, तो दोनों चरों के बीच सह-सम्बन्ध है ऐसा कहा जायेगा।

प्रश्न 2.
सह-सम्बन्ध गुणांक की परिभाषा दीजिए ।
उत्तर :
यादृच्छिक चर x और y के बीच समरेखीय सम्बन्ध के परिमाण के माप को सह-सम्बन्ध गुणांक (Correlation Coefficient) कहते हैं । उसे संकेत में r से दर्शाया जाता है ।
* निम्न दिये प्रश्न 3 से 6 में चल की दी गई युग्मों के बीच धनात्मक सम्बन्ध है या ऋणात्मक सम्बन्ध है वह बताइए ।

प्रश्न 3.
जीवन बीमा की किसी एक योजना के अंतर्गत बीमा लेते समय वयस्क व्यक्ति की उम्र और जीवन बीमा प्रीमियम ।
उत्तर :
जीवन बीमा की किसी एक योजना के अंतर्गत बीमा लेते समय वयस्क व्यक्ति की उम्र और जीवन बीमा प्रीमियम के बीच धनात्मक सह-सम्बन्ध है ।

प्रश्न 4.
किसी देश में अधिक प्रचलित वस्तु का अंतिम पाँच वर्ष का वार्षिक बिक्री और उससे होनेवाला लाभ ।
उत्तर :
किसी देश में अधिक प्रचलित वस्तु का अंतिम पाँच वर्ष का वार्षिक बिक्री और उससे होनेवाला लाभ के बीच धनात्मक सह सम्बन्ध है ।

प्रश्न 5.
किसी देश में सामान्य व्यक्ति की आय स्थिर हो तब मुद्रा स्फीति दर और उस देश के सामान्य व्यक्ति की क्रयशक्ति ।
उत्तर :
किसी देश में सामान्य व्यक्ति की आय स्थिर हो तब मुद्रा स्फिति दर और उस देश के सामान्य व्यक्ति की क्रयशक्ति के बीच ऋणात्मक सह-सम्बन्ध होगा ।

प्रश्न 6.
समुद्री सतह से स्थान की ऊँचाई और हवा में ऑक्सिजन का प्रमाण ।
उत्तर :
समुद्री सतह से स्थान की ऊँचाई और हवा में ऑक्सिजन का प्रमाण के बीच ऋणात्मक सह-सम्बन्ध होगा ।

प्रश्न 7.
क्रुड ओयल की वार्षिक आयात और उसी समय अंतराल में होती शादियाँ की संख्या के बीच के सह-सम्बन्ध के बारे में क्या कहा जा सकता है ?
उत्तर :
क्रुड ओयल की वार्षिक आयात और उसी समय अंतराल में होती शादियाँ की संख्या के बीच अर्थहीन सह-सम्बन्ध (मिथ्या) है ऐसा कहेंगे ।

प्रश्न 8.
x और y के बीच सह-सम्बन्ध गुणांक 0.4 है । अब x के प्रत्येक अवलोकन में 5 जोड़ा जाय और y के प्रत्येक अवलोकन में से 10 घटाया जाय तो सह-सम्बन्ध गुणांक क्या होगा ?
उत्तर :
सह-सम्बन्ध गुणांक पर उद्गमबिंदु और प्रमाप माप परिवर्तन का प्रभाव होता नहीं है इसलिए r = 0.4 होगा ।

प्रश्न 9.
विकीर्ण आकृति की मुख्य मर्यादा क्या है ?
उत्तर :
विकीर्ण आकृति पर से सह-सम्बन्ध की घनिष्ठता का कोई निश्चित अंक (माप) प्राप्त नहीं किया जा सकता ।

प्रश्न 10.
क्या दो सह-सम्बन्धित चल x और y के प्रमाप विचलनों का गुणाकार उसके सहविचरण के मूल्य से कम हो सकता है ? क्यों ?
उत्तर :
चल x और y के प्रमाप विचलनों का गुणाकार उसके सहविचरण के मूल्य में कम नहीं हो सकता क्योंकि सह-सम्बन्ध गुणांक का विस्तार -1 से 1 के बीच होता है ।

प्रश्न 11.
यदि n(n² – 1) का मूल्य Σd² के मूल्य से छ गुना हो, तो r का मूल्य कितना होगा ?
उत्तर :
यदि n(n² – 1) का मूल्य Σd² के मूल्य से छ गुना हो, तो r का मूल्य 0 होगा ।

प्रश्न 12.
यदि सहविचरण का मूल्य ऋण हो, तो r का चिन्ह क्या होगा ?
उत्तर :
यदि सहविचरण का मूल्य ऋण हो, तो r का चिन्ह ऋण होगा ।

विभाग – C

निम्न प्रश्नों के उत्तर दीजिए ।

प्रश्न 1.
धन सह-सम्बन्ध का अर्थ उदाहरण सहित समझाइए ।
उत्तर :
जब दो सह-सम्बन्धित चलों के मूल्य में होते परिवर्तन एक ही दिशा में होते हो तब दो चरों के बीच धनात्मक सह-सम्बन्ध है ऐसा कहा जाता है ।
वस्तु का मूल्य और पूर्ति, व्यक्ति की आय और खर्च पति की उम्र और पत्नी की उम्र, किसी विस्तार में वर्षा और गेहूँ की उपज धन सह-सम्बन्ध के उदाहरण है ।

प्रश्न 2.
ऋण सह-सम्बन्ध का अर्थ उदाहरण सहित समझाइए ।
उत्तर :
जब दो सह-सम्बन्धित चल के मूल्य में होते परिवर्तन एकदूसरे से विरुद्ध दिशा में हो तब दो चल के बीच ऋण सह-सम्बन्ध है ऐसा कहा जा सकता है ।
वस्तु का मूल्य और माँग व्यक्ति की बचत और खर्च, समुद्र स्तर से किसी स्थान की ऊँचाई और उसी स्थान के हवा में ऑक्सिजन ऋण सह-सम्बन्ध के उदाहरण है ।

प्रश्न 3.
कार्ल पियर्सन की विधि की परिकल्पनाएँ लिखिए ।
उत्तर :
कार्ल पियर्सन की विधि की परिकल्पनाएँ निम्नलिखित है :

1. दो चल के बीच समरेखीय सह-सम्बन्ध है ।
2. दो चल के बीच कार्य-कारण का सम्बन्ध है । यदि इस प्रकार का संबंध न हो, तो सहसंबंध अर्थहीन है । (मिथ्या)

प्रश्न 4.
विकीर्ण आकृति की परिभाषा दीजिए ।
उत्तर :
चर x के मानों को x-अक्ष पर और चर y के मानों का y-अक्ष पर, योग्य प्रमाणमाप (Scale) लेकर बिन्दुरेखीय पत्र पर n बिन्दुओं (x₁, y₁) (x₂, y₂) ………… (x_n, y_n) से निर्देशित करने से प्राप्त चित्र को विकीर्ण आरेख कहते हैं ।

प्रश्न 5.
अर्थहीन (मिथ्या) सहसंबंध अर्थात् क्या ?
उत्तर :
यदि दो चर के बीच कार्यकारण का संबंध न हो, तो दो चरों के बीच अर्थहीन सह-सम्बन्ध है ऐसा कहा जाता है जैसे अमेरिका में मोटर का उत्पादन में वृद्धि और भारत की जनसंख्या में वृद्धि के बीच अर्थहीन (मिथ्या) सह-सम्बन्ध है ऐसा कहेंगे ।

प्रश्न 6.
कार्यकारण का संबंध समझाइए ।
उत्तर :
सम्बन्धित चरों में से किसी एक चर की कीमत में कमी-वृद्धि होने से यदि दूसरे चर की कीमत में भी कमी-वृद्धि हो, तो दोनों चरों के बीच कार्य-कारण का सम्बन्ध है ऐसा कहा जायेगा । जैसे आय में वृद्धि होने के कारण खर्च में भी वृद्धि होगी।

प्रश्न 7.
संपूर्ण धन सह-सम्बन्ध समझाइए ।
उत्तर :
जब दो चरों के मान में परिवर्तन की दिशा समान हो तथा परिवर्तन का अनुपात भी समान हो तब उन दो चर x और y के बीच संपूर्ण धन सह-सम्बन्ध है ऐसा कहा जायेगा । यदि r = 1 हो तब संपूर्ण धन सह-सम्बन्ध होगा ।

प्रश्न 8.
संपूर्ण ऋणात्मक सह-सम्बन्ध समझाइए ।
उत्तर :
जब दो याद्दच्छिक चर के मान विपरीत दिशा में परिवर्तित होते हो और एक चर-मान इकाई में कमी-वृद्धि हो, तब दूसरे चर मान में किसी अचल अनुपात में कमी-वृद्धि होती हो, उन दो चरों के बीच संपूर्ण ऋणात्मक सह-सम्बन्ध है ऐसा कहेंगे । इसमें
r का मूल्य -1 होगा । r = -1 ।

प्रश्न 9.
क्रमांक सह-सम्बन्ध की आवश्यकता कब होती है ?
उत्तर :

1. जब अवलोकन गुणात्मक स्वरूप के दिये हो ।
2. अवलोकन को कोटियाँ दी गई हो ।
3. अवलोकनों में असमानता अधिक हो तब कोटि सह-सम्बन्ध की आवश्यकता होती है ।

प्रश्न 10.
कौन-से संयोगों में कार्ल पियर्सन की विधि और कोटि सह-सम्बन्ध की विधि से प्राप्त सह-सम्बन्ध गुणांक समान होता है ?
उत्तर :
जब दो चल के मूल्य प्रथम n प्राकृतिक संख्याओं की किसी रचना हो तब कार्ल पियर्सन की विधि द्वारा और स्पियरमेन से प्राप्त सह-सम्बन्ध गुणांक समान होते है ।

प्रश्न 11.
यदि Cov (x, y) = 120, Sx = 12, Sy = 15 r का मूल्य ज्ञात कीजिए ।
उत्तर :
r = \(\frac{{Cov}(\mathrm{x}, \mathrm{y})}{\mathrm{Sx} \cdot \mathrm{Sy}}\)
= \(\frac{120}{12 \times 15}\)
= \(\frac{120}{180}\)
= 0.67

प्रश्न 12.
यदि Σ(x – \(\overline{\mathbf{x}}\)) (y – \(\overline{\mathbf{y}}\)) = -65, Sx = 3, Sy = 4 और n = 10 हो, तो r का मूल्य ज्ञात कीजिए ।
उत्तर :
r = \(\frac{\sum(\mathrm{x}-\overline{\mathrm{x}})(\mathrm{y}-\overline{\mathrm{y}})}{\mathrm{n} \cdot \mathrm{Sx} \cdot \mathrm{Sy}}\)
= \(\frac{-65}{10 \times 3 \times 4}\)
= \(\frac{-65}{120}\)
= -0.54
∴ r = -0.54

प्रश्न 13.
10 अवलोकन के लिए Σd² = 120 हो, तो कोटि सह-सम्बन्ध का मूल्य ज्ञात कीजिए ।
उत्तर :
r = 1 – \(\frac{6 \sum d^2}{n\left(n^2-1\right)}\)
= 1 – \(\frac{6 \times 120}{10\left(10^2-1\right)}\)
= 1 – \(\frac{720}{10 \times 99}\)
= 1 – \(\frac{720}{10 \times 99}\)
= 1 – 0.3
= 0.27
∴ r = 0.27

विभाग – D

निम्न प्रश्नों के उत्तर दीजिए ।

प्रश्न 1.
विकीर्ण आकृति की विधि समझाइए ।
उत्तर :
दो सह-सम्बन्धवाले याद्दच्छिक चरों के बीच सह-सम्बन्ध का प्रकार जानने हेतु इस विधि का व्यापक रूप से उपयोग किया जाता है । तदुपरान्त यह विधि दो चरों के बीच सह-सम्बन्ध के परिणाम को भी प्रदर्शित करती है । दो सह-सम्बन्धित यादृच्छिक चरों में से एक चर को x और दूसरे चर को y संकेत से दर्शाया जाता है ।

चर x के मानों का x अक्ष पर और चर y के मानों का y अक्ष पर, योग्य प्रमाण माप (Scale) लेकर बिन्दुरेखीय पत्र पर n बिन्दुओं (x₁, y₁), (x₂, y) ……………. (x_n, y_n) से निर्देशित करने से प्राप्त चित्र को विकीर्ण आकृति कहते हैं ।

कभी-कभी इन बिन्दुओं के उपरांत समीप में से गुजरनेवाली सुरेखा या सरल वक्र रेखा भी प्रकीर्ण आरेन में निर्दष्ट करते है । प्रकीर्ण आकृति की सहायता से दोनों के बीच के सम्बन्ध का स्वरूप और सम्बन्ध का परिमाण जान सकते है ।

प्रश्न 2.
विकीर्ण आकृति के गुण-दोष बताइए ।
उत्तर :
गुण :

1. दो चल के बीच के सह-सम्बन्ध का स्वरूप जानने के लिए यह एक सरल विधि है ।
2. इस विधि में कम गाणितीय ज्ञान की आवश्यकता होती है ।
3. यह विधि से दो चल के बीच के सहसम्बन्ध की घनिष्टता का भी कुछ अंश तक ख्याल आता है ।
4. विकीर्ण आकृति में बिन्दु कैसे बिखरे हुए है । उस पर से दो चल के बीच का संबंध समरेखीय है या नहीं उसका विचार आता है ।

दोष :

1. सह-सम्बन्ध की घनिष्ठता का कोई निश्चित अंक (माप) प्राप्त नहीं किया जा सकता ।
2. इस विधि से मात्र सह-सम्बन्ध का प्रकार ज्ञात किया जा सकता है ।
3. वर्गीकृत द्विपदी सूचना के लिए यह विधि उपयोगी नहीं है ।

प्रश्न 3.
सह-सम्बन्धांक के गुणधर्म (विशेषताएँ) लिखिए ।
उत्तर :
सह-सम्बन्ध गुणांक की महत्त्वपूर्ण विशेषताएँ निम्नानुसार है :

1. सह-सम्बन्ध गुणांक r का महत्तम परिमाण 1 और न्यूनतम परिमाण -1 है । इस प्रकार -1 ≤ r ≤ 1 होगा ।
2. X और Y के बीच का सह-सम्बन्ध गुणांक r(x, y) और y एवं x के बीच का सह-सम्बन्ध गुणांक r(y, x) समान होते हैं । संकेत में r(x, y) = r(Y, X)
3. उद्गम बिन्दु और प्रमाण-माप दोनों के परिवर्तन का प्रभाव सह-सम्बन्ध गुणांक के परिमाण पर नहीं पड़ता अर्थात् r(x, y) = r(u, v)
4. सह-सम्बन्ध गुणांक के चिन्ह का आधार दोनों चलों के सह विचरण [Cov (x, y)] पर रहता है ।
5. सह-सम्बन्ध गुणांक r यह निरपेक्ष माप है ।
6. जब सह-सम्बन्ध गुणांक r = + 1 हो, तब धनात्मक सह-सम्बन्ध और जब r = -1 हो, तब ऋणात्मक सह-सम्बन्ध होगा ।

प्रश्न 4.
कार्ल पियर्सन की विधि के गुण-दोष बताइए ।
उत्तर :
गुण :

1. यह विधि द्वारा दो चल के बीच का सह-सम्बन्ध का प्रकार और उनके बीच के सम्बन्ध की घनिष्ठता भी जान सकते है ।
2. दो चर के बीच समरेखीय सह-सम्बन्ध मापने की यह सबसे प्रचलित विधि है ।
3. यह सह-सम्बन्ध की घनिष्ठता को संख्या में दर्शाता है ।

दोष :

1. यह विधि परिकल्पना पर आधारित है कि दो चल के बीच समरेखीय सह-सम्बन्ध है । यदि समरेखीय सह-सम्बन्ध न हो, तो यह विधि से ज्ञात सह-सम्बन्ध गुणांक का अर्थघटन किया जाय तो ऐसा अर्थघटन अर्थहीन है ।
2. सह-सम्बन्ध के मूल्य पर अंतिम अवलोकनों का प्रभाव अधिक होता है ।

प्रश्न 5.
r = 1, r = -1 और r = 0 का अर्थघटन कीजिए ।
उत्तर :
(1) r = 1 : जब r = 1 हो, तब दिए गए चर X और Y के बीच संपूर्ण धन समरेख सह-सम्बन्ध है, ऐसा कहा जायेगा । X और Y के बीच इस सम्बन्ध को Y = a + bx (अथवा X = c + dY) समीकरण से प्रदर्शित किया जाता है, जहाँ अचलांक b (अथवा d) का मान धनात्मक है । अचल b को सुरेखा Y = a + bx का ढाल कहते है, जो यहाँ धन है । जब प्रकीर्ण आरेख चित्र में समग्र बिन्दु एक सुरेखा पर आए हों और उस सुरेखा की ढाल धन हो, अर्थात् सुरेखा बाई ओर से दाई ओर, नीचे से ऊपर की ओर जाती हो तब r = 1 होता है ।

(2) r = -1 : चर X और Y के बीच संपूर्ण ऋणात्मक समरेखीय सह-सम्बन्ध हो, तब दी गई सूचना के लिए r = -1 होता है । X और Y के बीच इस प्रकार के सम्बन्ध को Y = a + bx (अथवा X = c + dx) समीकरण द्वारा प्रदर्शित किया जाता है । यहाँ b (अथवा d) का मान ऋणात्मक होता है । सुरेखा Y = a + bx को ढाल कहा जाता है, जो यहाँ ऋणात्मक है । जब प्रकीर्ण आरेन चित्र में स्थित समग्र बिन्दु बाई ओर से दाई ओर, ऊपर से नीचे की दिशा में जानेवाली सुरेखा पर हो, तब r = -1 होगा ।

(3) r = 0 : जब X और Y के बीच समरेखीय सह-सम्बन्ध का अभाव हो, तब r = 0 होगा । जब प्रकीर्ण आरेख चित्र में सभी बिन्दु कोई एक सुरेखा बनाने में असमर्थ हो तब r = 0 होगा ।

प्रश्न 6.
स्पियरमैन की क्रमांक सह-सम्बन्ध की विधि समझाइए ।
उत्तर :
जब इकाई के लिए दी गई सूचना दो चर (या गुण) मापक – साधन द्वारा माप प्रदर्शित करनेवाली संख्या के स्वरूप में न हो, परंतु इनको दी गई कोटि के स्वरूप में हो, तब दो चरों के बीच सह-सम्बन्ध गुणांक की गणना चार्ल्स स्पियरमैन (Charles Spearman) नामक सांख्याविद द्वारा सूचित विधि से की जाती है ।

इस विधि के अनुसार सर्वप्रथम दी गई गुणात्मक सूचनाओं को उनके गुण के आधार पर कोटि या क्रमांक दिया जाता है । इस प्रकार दो निर्णायकों या विशेषज्ञों द्वारा दी गई कोटि के बीच का अन्तर d ज्ञात किया जाता है, इस प्रकार d = R_x – R_y होगा । इस प्रकार प्राप्त किये गए कोटि अन्तर का वर्ग (d²) ज्ञात किया जाता है । कोटि के अन्तर का वर्गों के योग ज्ञात किया जाता है और निम्न सूत्र की मदद से स्पियरमैन का कोटि सह-सम्बन्ध गुणांक r का परिकलन किया जाता है ।
r = 1 \(\left\{\frac{6 \sum d^2}{n\left(n^2-1\right)}\right\}\)

प्रश्न 7.
स्पियरमैन की क्रमांक सह-सम्बन्ध की विधि के गुण-दोष बताइए ।
उत्तर :
गुण :

1. कार्ल पियर्सन की गुणन-प्रधान की विधि की अपेक्षा यह विधि समझने में और परिकलन में सरल है ।
2. साक्षात्कार, सौंदर्य-स्पर्धा, वक्तृत्व स्पर्धा, अभिनय-स्पर्धा, संगीत व नृत्य जैसी स्पर्धाओं में इकाइयों गुणात्मक होने से यह विधि अधिक योग्य है ।
3. जब माहिती संख्यात्मक हो तब भी इस विधि द्वारा सहसम्बन्ध प्राप्त किया जा सकता है ।
   जब प्राप्तांकों के बदले मात्र उनकी कोटियाँ दी गई हो तब इस विधि से सह-सम्बन्ध गुणांक ज्ञात किया जा सकता है ।

दोष :

1. इस विधि द्वारा प्राप्त सह-सम्बन्ध गुणांक कार्ल पियर्सन द्वारा प्राप्त सह-सम्बन्ध गुणांक जितना सटीक नहीं होता है ।
2. जब अवलोकनों की माहिती अधिक संख्या में हो तब, कोटि देने का कार्य कठिनाई युक्त और निरस बन जाता है ।

प्रश्न 8.
आंशिक सह-सम्बन्ध का अर्थघटन आप कैसे करोगे ?
उत्तर :
सह-सम्बन्ध के सीमांत (आंशिक) परिमाण दो प्रकार के हो सकते हैं ।
(1) आंशिक धन सह-सम्बन्ध (Partial Positive Correlation)
(2) आंशिक ऋणात्मक सह-सम्बन्ध (Partial Negative Correlation)

(1) आंशिक धन सह-सम्बन्ध : जब दो चरों के मान में परिवर्तन की दिशा समान हो, परंतु परिवर्तन का अनुपात समान न हो, तब दोनों चर X और Y के बीच आंशिक धन सह-सम्बन्ध है, ऐसा कहा जायेगा । इसमें r की कीमत 0 से अधिक परंतु 1 से कम होता है । आंशिक धन सह-सम्बन्ध को संकेत में 0

(2) आंशिक ऋणात्मक सह-सम्बन्ध : जब दो याच्छिक चर मान विपरीत दिशा में परिवर्तित होते हो, परंतु दोनों चरों की इकाई में होनेवाली वृद्धि-कमी का अनुपात समान (अचल) न हो, तो उन दोनों चरों के बीच आंशिक ऋमात्मक सह-सम्बन्ध है, ऐसा
कहा जायेगा । इसमें r की कीमत 0 से कम परंतु -1 से अधिक होती है । अर्थात् -1 < r < 0 होगा ।

प्रश्न 9.
सह-सम्बन्ध गुणांक के अर्थघटन में रखने योग्य सावधानियाँ बताइए ।।
उत्तर :
दो याच्छिक चरों के बीच समरेखीय सह-सम्बन्ध के परिमाण का माप सह-सम्बन्ध गुणांक के लिए अत्यन्त उपयोगी है । इसलिए इस माप का योग्य रूप से अर्थघटन होना आवश्यक है । अन्यथा यह गलत मार्गदर्शन करके दोनों चरों के बीच गलतफहमी भी फैला सकता है, परिणामस्वरूप सह-सम्बन्ध गुणांक का अर्थघटन करते समय निम्न सावधानियाँ रखनी चाहिए ।

(1) अर्थशून्य सह-सम्बन्ध गुणांक (Naisance Correlation) सम्बन्धी सावधानियाँ : सह-सम्बन्ध गुणांक का अर्थघटन तभी योग्य कहलायेगा जब दोनों चलों के बीच कार्य-कारण का सम्बन्ध है । कई बार दो चल जिनके बीच कार्य-कारण का सम्बन्ध न हो ऐसी माहिती पर से प्राप्त किया सह-सम्बन्ध गुणांक का अर्थघटन अयोग्य मार्गदर्शन दे सकता है । जैसे कि अमेरिका में प्रति व्यक्ति आय (X) और भारत में केन्सर से मरनेवाले मरीजों की संख्या (Y) के बीच किसी समय – अन्तराल में लिए गए अवलोकनों के मानों से परिकलन किया गया सह-सम्बन्ध गुणांक का परिमाण 1 के समीप हो सकता है, परंतु यहाँ चर X और Y के बीच कोई अर्थपूर्ण सम्बन्ध नहीं है । ऐसे उदाहरण से प्राप्त सह-सम्बन्ध गुणांक का परिमाण अर्थशून्य या मिथ्या सह-सम्बन्ध (Nuisance Correlation) है, ऐसा कहा जाएगा ।

(2) सह-सम्बन्ध गुणांक का अभाव या r = 0 के अर्थघटन में सावधानी : जब r = 0 हो, तो ऐसा कहना कि दोनों चरों के बीच कोई सह-सम्बन्ध नहीं है योग्य नहीं होगा, क्योंकि r = 0 हो इस दशा में हम मात्र इतना ही कह सकते हैं कि, दिए गए चरों X और Y के बीच समरेखीय सह-सम्बन्ध नहीं है, लेकिन समरेखीय सह-सम्बन्ध के अलावा द्विघातीय या चक्रीय या अन्य प्रकार का सह-सम्बन्ध हो सकता है।

(3) अर्थघटन के विस्तार में सावधानी : जिस विस्तार, वर्ग या समय दौरान न्यादर्श सूचना प्राप्त की हो, उसी तक ही सह-सम्बन्ध गुणांक की परिमाण का अर्थघटन सीमित रखना योग्य रहेगा ।

प्रश्न 10.
दो चल वर्षा मि.मि. में (X) और फसल की उपज क्विन्टल/हेक्टर (Y) की निम्न सचना प्राप्त हुई है।
n = 10, \(\overline{\mathrm{x}}\) = 120, \(\overline{\mathrm{y}}\) = 150, Sx = 30, Sy = 40 और Σxy = 189000 पर से सह-सम्बन्ध गुणांक ज्ञात कीजिए ।
उत्तर :
यहाँ निम्न सूत्र का उपयोग करेंगे ।
r = \(\frac{\sum x y-n \bar{x} \bar{y}}{n \cdot S x \cdot S y}\)
= \(\frac{189000-10 \times 120 \times 150}{10 \times 30 \times 40}\)
= \(\frac{189000-180000}{12000}\)
= \(\frac{9000}{12000}\)
= 0.75
∴ r = 0.75

प्रश्न 11.
अवलोकन के लिए निम्नानुसार सूचना प्राप्त हुई है ।
Σx = 51, Σy = 72, Σx² = 315, Σy² = 582, Σxy = 408 इस सूचना पर से सहसम्बन्ध गुणांक ज्ञात कीजिए ।
उत्तर :
यहाँ निम्न सूत्र का उपयोग करेंगे ।

∴ r = 0

प्रश्न 12.
एक नृत्य स्पर्धा में आठ स्पर्धकों को दो निर्णायक द्वारा दिया क्रम पर से निम्न सूचना मिली है ।
Σ(R_x – R_y)² = 126
जहाँ R_x और R_y दो निर्णायकों द्वारा दी गई कोटियाँ दर्शाते है, उस पर से कोटि सह-सम्बन्ध गुणांक ज्ञात कीजिए ।
उत्तर :
यहाँ Σ(R_x – R_y)² = 126 दिया है अर्थात् Σd² = 126, n = 8 है । कोटि सह-सम्बन्ध गुणांक निम्न सूत्र से ज्ञात करेंगे ।
r = 1 – \(\frac{6 \sum \mathrm{d}^2}{\mathrm{n}\left(\mathrm{n}^2-1\right)}\)
= 1 – \(\frac{6 \times 126}{8\left(8^2-1\right)}\)
= 1 – \(\frac{756}{8 \times 63}\)
= 1 – \(\frac{756}{504}\)
= 1 – 1.5
∴ r = -0.5

प्रश्न 13.
नौकरी के साक्षात्कार में दो निर्णय द्वारा दी गई कोटियाँ (3, 5), (5, 4), (1, 2), (2, 3) और (4, 1) है । इस सूचना पर से कोटि सह-सम्बन्ध गुणांक ज्ञात कीजिए ।
उत्तर :
कोटियाँ दी गई है इस लिए निम्न सारणी बनायेंगे ।

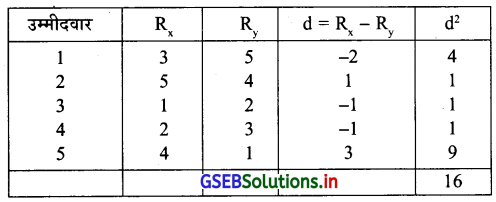
r = 1 – \(\frac{6 \sum d^2}{n\left(n^2-1\right)}\)
= 1 – \(\frac{6 \times 16}{5\left(5^2-1\right)}\)
= 1 – \(\frac{96}{5 \times 24}\)
= 1 – \(\frac{96}{120}\)
= 1 – 0.8
∴ r = 0.2

विभाग – E

निम्न प्रश्नों के उत्तर दीजिए ।

प्रश्न 1.
महामारी के फैलाव के समय दौरान नाक पर पहने के मास्क की बिक्री मूल्य और उसकी माँग के बीच का सम्बन्ध जानने हेतु एकत्रित की गई सूचना पर से मास्क का मूल्य और माँग के बीच कार्ल पियर्सन की विधि से सह-सम्बन्ध गुणांक ज्ञात कीजिए।

उत्तर :
n = 5, \(\bar{x}=\frac{\sum x}{n}=\frac{200}{5}\) = 40, \(\bar{y}=\frac{\sum y}{n}=\frac{490}{5}\) = 98
यहाँ \(\overline{\mathrm{x}}\) और \(\overline{\mathrm{y}}\) पूर्णांक में है इसलिए हम निम्नानुसार सारणी से r ज्ञात करेंगे ।

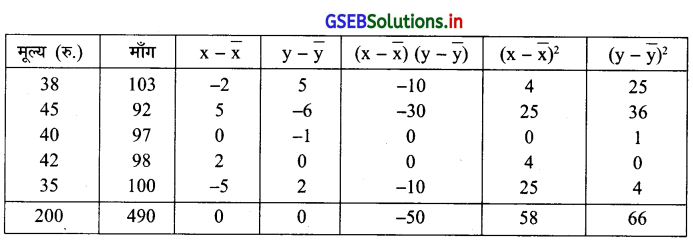
r = \(\frac{\sum(\mathrm{x}-\overline{\mathrm{x}})(\mathrm{y}-\overline{\mathrm{y}})}{\sqrt{\sum(\mathrm{x}-\overline{\mathrm{x}})^2} \times \sqrt{\sum(\mathrm{y}-\overline{\mathrm{y}})^2}}\)
= \(\frac{-50}{\sqrt{58} \times \sqrt{66}}\)
= \(\frac{-50}{\sqrt{3828}}\)
= \(\frac{-50}{61.87}\)
= r = -0.81

प्रश्न 2.
एक अनुस्नातक कक्षा के अभ्यास में विद्यार्थियों को मानव संसाधन संचालन और व्यक्तित्व विकास जैसे विषयों में उनकी क्षमता के बीच सम्बन्ध जानने के लिए पाँच विद्यार्थियों को न्यादर्श लेकर निम्न सूचना प्राप्त हुई है :

इस सूचना पर से दोनों विषय के नंबर के बीच कार्ल पियर्सन की विधि से सह-सम्बन्ध गुणांक ज्ञात कीजिए ।
उत्तर :
यहाँ n = 5, \(\) = 35, \(\) = 34
\(\overline{\mathrm{x}}\) और \(\overline{\mathrm{y}}\) पूर्णांक है इसलिए निम्नानुसार सारणी बनाकर r ज्ञात करेंगे ।

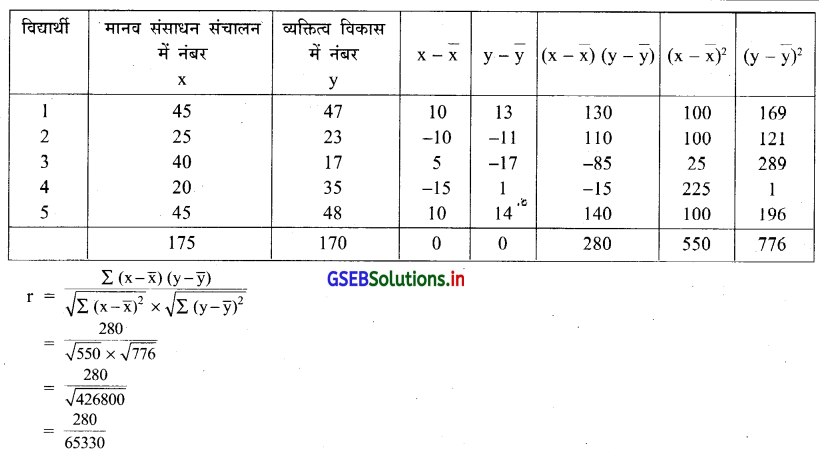
= 0.43
∴ r = 0.43

प्रश्न 3.
एक विक्रेता विविध ब्रान्ड की लिपस्टिक उसकी लोकप्रियता अनुसार शॉकेस में प्रदर्शित करने की इच्छा है इसलिए भिन्न भिन्न ब्रान्ड की लिपस्टिक को क्रम देने के लिए दो विशेषज्ञ प्रेयल और निशी को आमंत्रित करते है ।

उपर्युक्त दो विशेषज्ञों द्वारा दिए कोटियाँ की साम्यता जानने के लिए कोटि सहसम्बन्ध गुणांक ज्ञात कीजिए।
उत्तर :
यहाँ n = 7 कोटियाँ दी गई है । इसलिए कोटि सह-सम्बन्ध गुणांक ज्ञात करने के लिए निम्नानुसार सारणी बनायेंगे ।

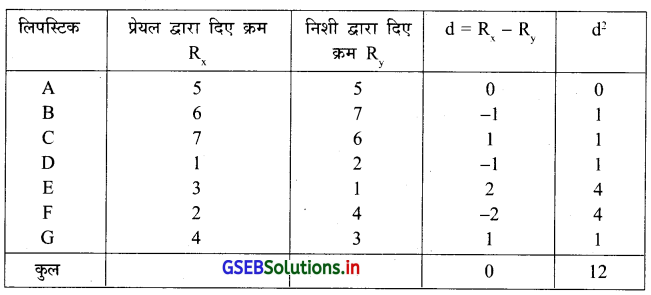
r = 1 – \(\left\{\frac{6 \sum \mathrm{d}^2}{\mathrm{n}\left(\mathrm{n}^2-1\right)}\right\}\)
= 1 – \(\frac{6 \times 12}{7\left(7^2-1\right)}\)
= 1 – \(\frac{72}{7 \times 48}\)
= 1 – \(\frac{72}{336}\)
∴ r = 1 – 0.21
∴ r = 0.79

प्रश्न 4.
अहमदाबाद शहर में चाय का मूल्य (कि.ग्रा. में) और कोफी का मूल्य (100 ग्राम में) के बीच का सम्बन्ध जानने हेतु एक वेपारी भिन्न-भिन्न प्रकार की चाय और कोफी के मूल्यों की निम्न सूचना पर से क्रमांक सह-सम्बन्ध गुणांक ज्ञात कीजिए।

उत्तर :
यहाँ n = 6 संख्यात्मक चर दिया है इसलिए सर्वप्रथम क्रमांक देंगे । सबसे बड़ी संख्या से शुरुआत करके निम्नानुसार क्रमांक देंगे ।

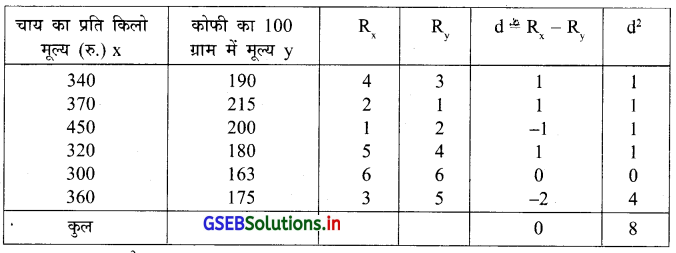
r = 1 – \(\frac{6 \sum d^2}{n\left(n^2-1\right)}\)
= 1 – \(\frac{6 \times 8}{6\left(6^2-1\right)}\)
= 1 – \(\frac{48}{6 \times 35}\)
= 1 – \(\frac{48}{210}\)
= 1 – 0.23
r = 0.77
∴ r = 0.77

प्रश्न 5.
एक विदेशी फल की स्थानिक बाजार में अधिक अनिश्चित माँग दिखाई देता है, फल का एक विक्रेता उस विदेशी फल का मूल्य और पूर्ति के बीच सम्बन्ध जानने के लिए निम्नानुसार पिछले दस मास के औसत मूल्य और पूर्ति की सूचना प्राप्त की है।

उपयुक्त सूचना पर से मूल्य और पूर्ति के बीच क्रमांक सह-सम्बन्ध गुणांक ज्ञात कीजिए ।
उत्तर :
यहाँ n = 10 संख्यात्मक चर दिया है इसलिए सर्वप्रथम सबसे बड़ी संख्या से शुरूआत करके क्रमांक देंगे ।

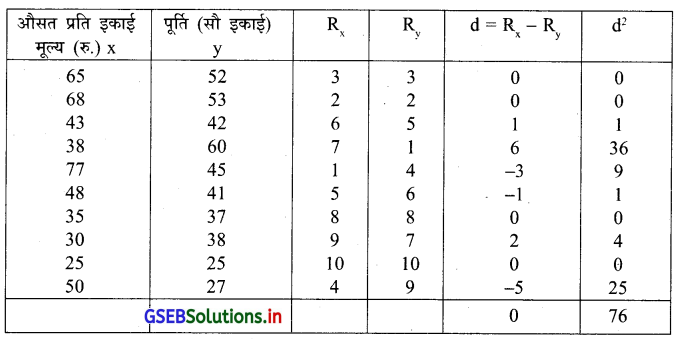
r = 1 – \(\frac{6 \sum d^2}{n\left(n^2-1\right)}\)
= 1 – \(\frac{6 \times 76}{10\left(10^2-1\right)}\)
= 1 – \(\frac{456}{10 \times 99}\)
= 1 – \(\frac{456}{990}\)
= 1 – 0.46
= 0.54
∴ r = 0.54

प्रश्न 6.
कम समय अंतराल में विद्यार्थियों की परीक्षा ली जाय तो परिणामों के बीच सम्बन्ध जानने हेतु एक शिक्षक अंतिम दो सप्ताह में ली गई दो परीक्षा के परिणाम पर से सात विद्यार्थियों के क्रमांक निम्नानुसार प्राप्त हुई ।

इस सूचना पर से दो परीक्षा के परिणाम के बीच समानता जानने के लिए क्रमांक सह-सम्बन्ध गुणांक ज्ञात कीजिए ।
उत्तर :
n = 7 प्रथम परीक्षा में दो कोटियाँ समान 3.5 है । क्रमांक दी गई है इसलिए निम्नानुसार सारणी बनायेंगे ।
‘CF’ की गणना निम्नानुसार करेंगे ।

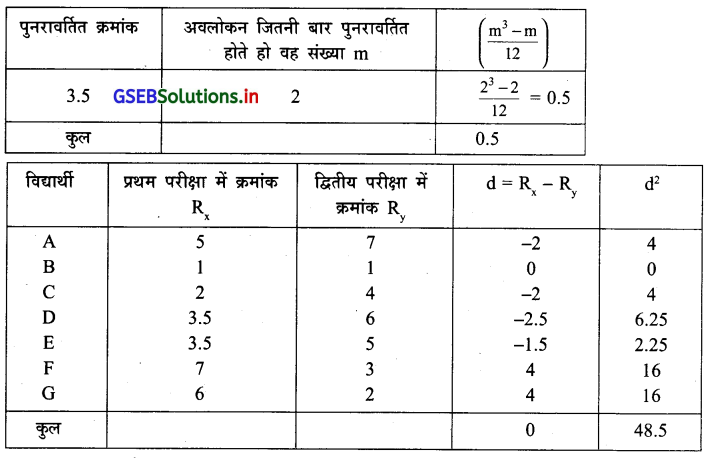
r = 1 – \(\frac{6\left[\sum \mathrm{d}^2+\mathrm{cf}\right]}{\mathrm{n}\left(\mathrm{n}^2-1\right)}\)
= 1 – \(\frac{6(48.5+0.5)}{7\left(7^2-1\right)}\)
= 1 – \(\frac{6(49)}{7(48)}\)
= 1 – \(\frac{294}{336}\)
= 1 – 0.875 = 0.125
∴ r = 0.13

विभाग – F

निम्न प्रश्नों के उत्तर दीजिए ।

प्रश्न 1.
आठ जिले में खाद का उपयोग (टन में) और उत्पादकता (टन में) की निम्न सूचना पर से कार्ल पियर्सन की विधि से सहसम्बन्ध गुणांक ज्ञात कीजिए ।

उत्तर :
यहाँ n = 8, \(\bar{x}=\frac{\sum x}{n}=\frac{220}{8}\) = 27.5, \(\frac{\sum y}{n}=\frac{908}{8}\) = 113.5
\(\overline{\mathrm{x}}\) और \(\overline{\mathrm{y}}\) अपूर्णांक में है इसलिए r ज्ञात करने के लिए निम्नानुसार सारणी बनाएँगे ।


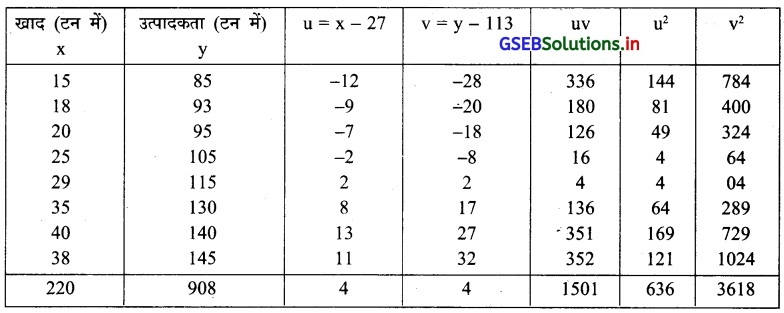
= 0.99
∴ r = 0.99
खाद का उपयोग और उत्पादकता के बीच घनिष्ठ धन सहसम्बन्ध है ।

प्रश्न 2.
एक बड़े शहर के छ बालकों द्वारा विडियो गेम्स खेलने के लिए सप्ताह में औसत घण्टे और एक परीक्षा में प्राप्त अंक (Grade Point) के बीच निम्न सूचना पर से कार्ल पियर्सन की विधि से सहसम्बन्ध गणांक ज्ञात कीजिए ।

उत्तर :
यहाँ n = 6 और \(\bar{x}=\frac{\sum x}{n}=\frac{276}{6}\) = 46, \(\overline{\mathrm{y}}=\frac{\sum \mathrm{y}}{\mathrm{n}}=\frac{29.5}{6}\) = 4.92
\(\overline{\mathrm{x}}\) और \(\overline{\mathrm{y}}\) अपूर्णांक में है । चल y की कीमत में दशांश के बाद एक अंक है इसलिए पूर्णांक बनाने के लिए 10 से गुणा करेंगे ।
A = 46 और B = 4.9 लेंगे । नया चल u = x – 46 और v = 10(y – 4.9)

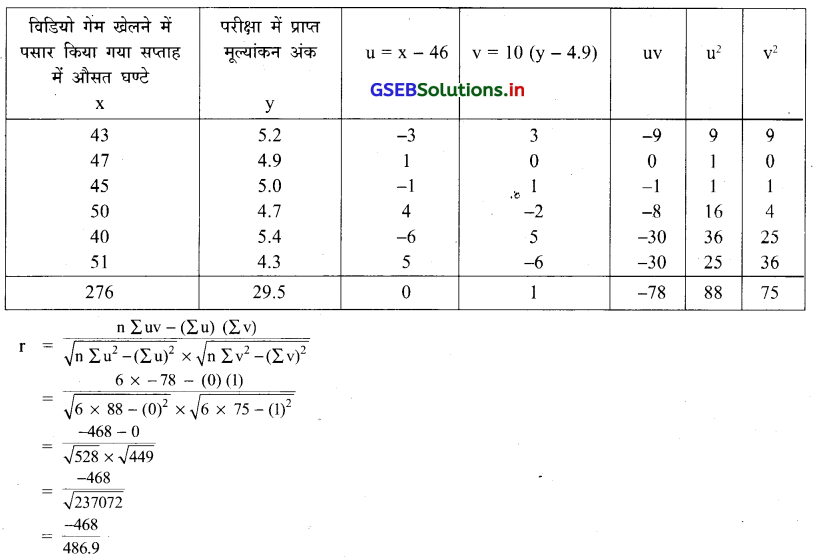
= -0.96
∴ r = 0.96
x और y के चल के बीच घनिष्ठ सह-सम्बन्ध है ।

प्रश्न 3.
निम्न सूचना पर से जनसंख्या की घनिष्ठता (चो.कि.) और मृत्युदर (दर हजार) के बीच कार्ल पियर्सन की विधि से सह सम्बन्ध गुणांक ज्ञात कीजिए ।

उत्तर :
यहाँ n = 7, \(\bar{x}=\frac{\Sigma x}{n}=\frac{3950}{7}\) = 564.29, \(\bar{y}=\frac{\sum y}{n}=\frac{170}{7}\) = 24.29
यहाँ \(\overline{\mathrm{x}}\) और \(\overline{\mathrm{y}}\) अपूर्णांक में है इस लिए कार्ल पियर्सन की संक्षिप्त विधि का उपयोग करेंगे । x(घनिष्टता) के अवलोकन को 50 से भाग दे सकते है और y (मृत्युदर) को 5 से भाग दे सकते है, A = 550 और B = 25 लेकर नया चर u = \(\frac{\mathrm{x}-\mathrm{A}}{\mathrm{Cx}}\) और v = \(\frac{\mathrm{y}-\mathrm{B}}{\mathrm{Cy}}\) प्राप्त करेंगे । Cx = 50 और Cy = 5 लेकर u = \(\frac{x-550}{50}\), v = \(\frac{\mathrm{y}-25}{5}\) से नया चर प्राप्त करेंगे ।


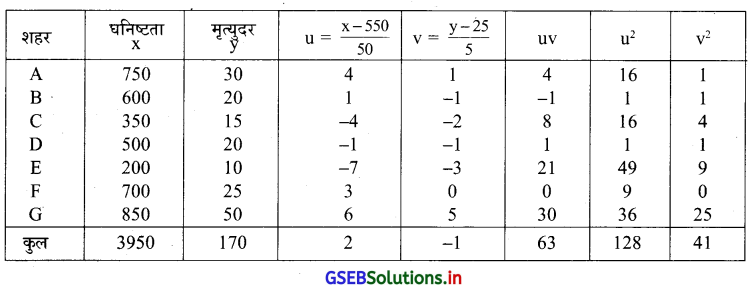
= 0.88
∴ r = 0.88
घनिष्ठता और मृत्युदर के बीच घनिष्ठ सह-सम्बन्ध है ।

प्रश्न 4.
इलेक्ट्रिक पंखे का उत्पादन करती कंपनीओं की विज्ञापन खर्च और बिक्री के बीच संबंध का अध्ययन करने के लिए निम्नानुसार सूचना एकत्रित की गई । उस सूचना पर से विज्ञापन खर्च और बिक्री के बीच का सह-सम्बन्ध गुणांक कार्ल पियर्सन की विधि से ज्ञात कीजिए ।

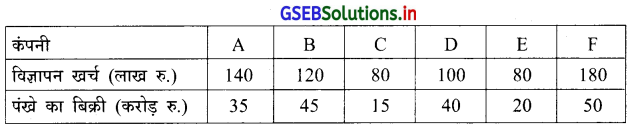
उत्तर :
यहाँ n = 6, \(\bar{x}=\frac{\Sigma x}{n}=\frac{700}{6}\) = 116.67, \(\overline{\mathrm{y}}=\frac{\sum \mathrm{y}}{\mathrm{n}}=\frac{205}{7}\) = 34.17 .
यहाँ \(\overline{\mathrm{x}}\) और \(\overline{\mathrm{y}}\) अपूर्णांक में है इसलिए कार्ल पियर्सन की संक्षिप्त विधि का उपयोग करेंगे । विज्ञापन खर्च को 10 से भाग दे सकते है और पंखे की बिक्री को -5 से भाग देकर निम्नानुसार सारणी बनायेंगे । यहाँ A = 110 और B = 35 लेकर u = \(\frac{\mathrm{x}-\mathrm{A}}{\mathrm{Cx}}\) और v = \(\frac{\mathrm{y}-\mathrm{B}}{\mathrm{Cy}}\) । जहाँ Cx = 10 और Cy = 5 लेकर नया चर निम्नानुसार प्राप्त करेंगे । u = \(\frac{x-110}{10}\), v = \(\frac{y-35}{5}\)

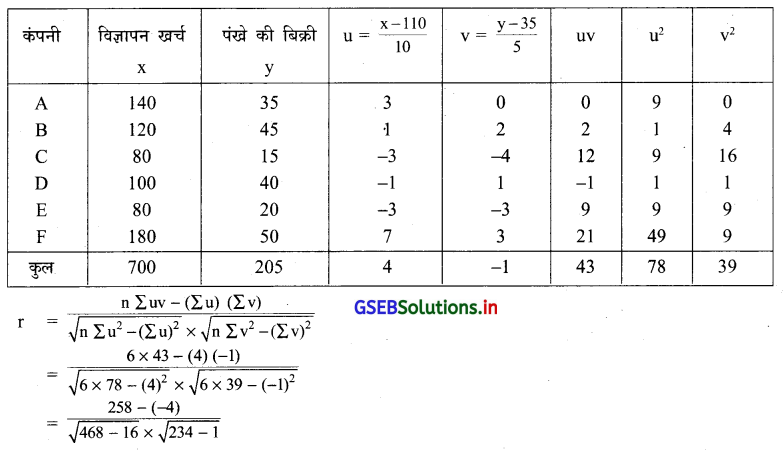
= \(\frac{262}{\sqrt{452} \times \sqrt{233}}\)
= \(\frac{262}{\sqrt{105316}}\)
= \(\frac{262}{324.52}\)
r = 0.8073
∴ r = 0.81
विज्ञापन खर्च और पंखे की बिक्री के बीच आंशिक धन सह-सम्बन्ध है ।

प्रश्न 5.
एक डॉक्टर एक संशोधन कार्य के लिए बालक के जन्म समय बालक और उनकी माता का वजन के बीच का संबंध जानने हेतु एक विस्तार के कुछ मेटरनीटी होम में से सात माता और उनके बालक का वजन की निम्न सूचना पर से क्रमांक सहसम्बन्ध गुणांक ज्ञात कीजिए ।

उत्तर :
यहाँ n = 7 और संख्यात्मक चर दिया है । इस पर से सर्वप्रथम सबसे बड़ी संख्या से शुरुआत करके कोटियाँ देंगे । माता का वजन में 66 को दो बार पुनरावर्तन होता है । गणना के लिए निम्नानुसार सारणी बनायेंगे ।

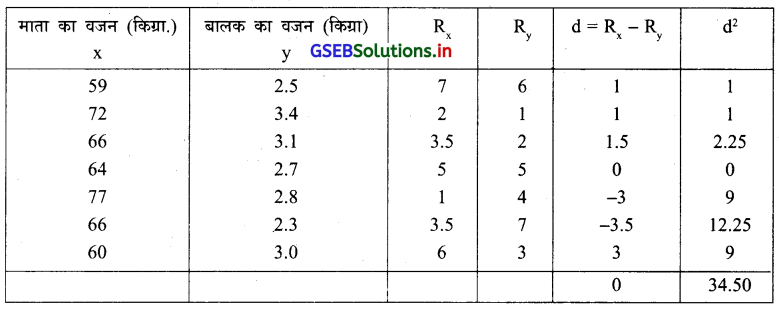
‘CF’ की गणना निम्नानुसार करेंगे ।

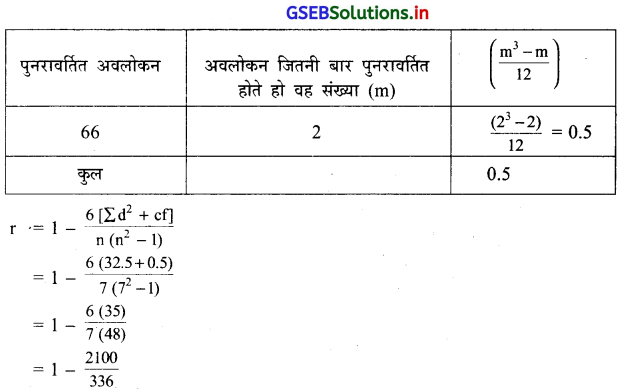
= 1 – 0.625
= 0.375
∴ r = 0:38

प्रश्न 6.
अहमदाबाद में दिन का महत्तम तापमान और आईस्क्रीम की बिक्री के बीच सम्बन्ध जानने हेतु निम्न सूचना प्राप्त की गई है ।

उपयुक्त सूचना पर से क्रमांक सह-सम्बन्ध गुणांक की गणना करो ।
उत्तर :
यहाँ n = 8 और सूचना संख्यात्मक दी गई है । इसलिए सबसे बड़ी संख्या से शुरुआत करके क्रम देंगे । यहाँ 40 का तीन बार पुनरावर्तन होता है । 40 का क्रम की औसत \(\frac{4+5+6}{3}=\frac{15}{3}\) = 5 देंगे और 750 का दो बार पुनरावर्तन होता है ।

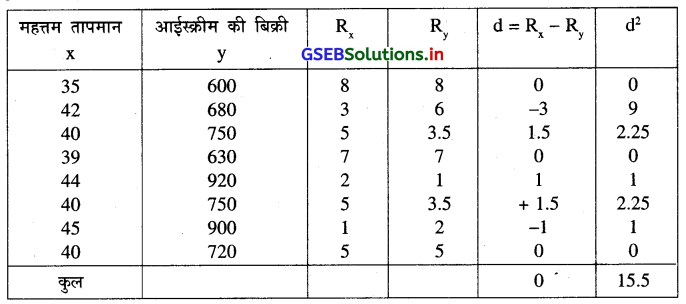
‘CF’ की गणना निम्नानुसार करेंगे ।

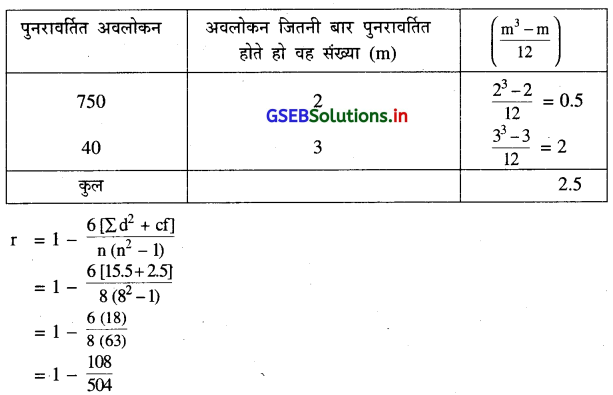
= 1 – 0.21
= 0.79
∴ r = 0.79

प्रश्न 7.
विदेश में अध्ययन करने हेतु आवश्यक परीक्षा ओनलाईन ली जाती है । ओनलाईन परीक्षा में (यदि गलत उत्तर हो, तो ऋण नंबर मिलता है ऐसी पद्धति है ।) में न्यादर्श में चयन हुए पाँच विद्यार्थियों द्वारा स्वयंसूझ (Reasoning ability) और इंग्लिश बोलने की सूझ में प्राप्त अंक निम्नानुसार है ।

उपयुक्त सूचना पर से क्रमांक सह-सम्बन्ध गुणांक ज्ञात कीजिए ।
उत्तर :
यहाँ n = 5 और सूचना संख्यात्मक दी गई है । इसलिए सर्वप्रथम कोटियाँ देंगे । सारणी निम्नानुसार प्राप्त होगी ।

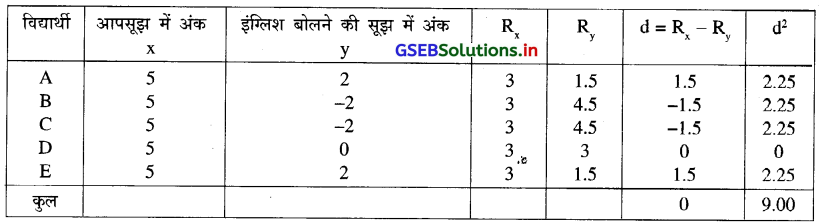
‘CF’ की गणना निम्नानुसार करेंगे ।

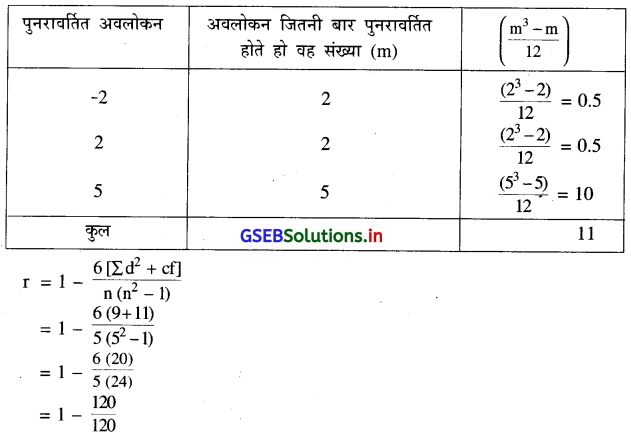
= 1 – 1
r = 0
∴ r = 0
दो चरों के बीच समरेखीय सह-संबंध का अभाव है ऐसा कहेंगे ।

प्रश्न 8.
एक नृत्य की स्पर्धा में दो नृत्य गुरु ने छ नृत्यकार A, B, C, D, E और F को निम्नानुसार क्रम दिए है ।

उपयुक्त सूचना पर से दोनों गुरु के मूल्यांकन के बीच क्रमांक सह-सम्बन्ध गुणांक ज्ञात कीजिए ।
उत्तर :
यहाँ n = 6 सूचना के आधार से दी गई कोटियाँ को फिर से गठन करने पर

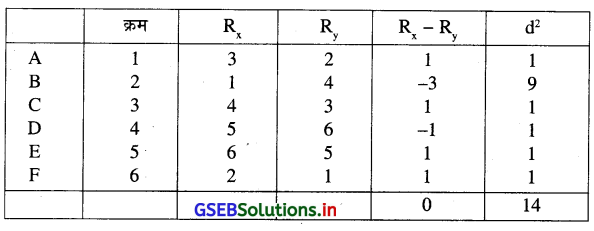
r = 1 – \(\frac{6 \sum d^2}{n\left(n^2-1\right)}\)
= 1 – \(\frac{6 \times 14}{6\left(6^2-1\right)}\)
= 1 – \(\frac{84}{6 \times 35}\)
= 1 – \(\frac{84}{210}\)
= 1 – 0.4
= 0.6
∴ r = 0.6

प्रश्न 9.
दो चल x (मुद्रास्फिति) और ब्याजदर (y) की निम्न सूचना मिली है ।
n = 50, Σ50 = 500, Σy = 300, Σx² = 5450, Zy² = 2000, Σxy = 3090 बाद में पता चला कि एक युग्म (10, 6) गलती से अधिक ली गई थी उसे निकालकर नया सह-सम्बन्ध गुणांक ज्ञात कीजिए ।
उत्तर :
r = \(\frac{n \sum x y-\left(\sum x\right)\left(\sum y\right)}{\sqrt{n \sum x^2-\left(\sum x\right)^2} \times \sqrt{n \sum y^2-\left(\sum y\right)^2}}\)
सुधार करने के बाद सही मूल्य (10, 6) को निकालने के बाद सही
n = 50 – 1 = 49
Σx = 500 – 10 = 490
Σy = 300 – 6 = 294
Σx² = 5450 – (10)²
= 5450 – 100
= 5350

Σy² = 2000 – (6)²
= 2000 – 36
= 1964

Σxy = 3090 – (10) (6)
= 3090 – 60
= 3030
n = 50
सूत्र में रखने पर

r = 0.3
∴ r = 0.3

प्रश्न 10.
दस पेढ़ी के लिए बिक्री (x) और खर्च (y) की निम्न सूचना पर से सह-सम्बन्ध गुणांक ज्ञात कीजिए ।
\(\overline{\mathrm{x}}\) = 58, \(\overline{\mathrm{y}}\) = 14, Σ(x – 65)² = 850, Σ(y – 13)² = 32, Σ(x – 65) (y – 13) = 0
उत्तर :
\(\overline{\mathrm{x}}\) = 58 और A = 65 एवं \(\overline{\mathrm{y}}\) = 14 और B = 13 है । विचलन माध्य में से लिया नहीं है । इसलिए u = X – A एवं
B = y – B पारिभाषित करना अनुकूल रहेगा ।
r का सूत्र का उपयोग करने के लिए सर्वप्रथम Σu और Σv ज्ञात करेंगे ।

= 0.787
∴ r = 0.79

प्रश्न 11.
10 व्यक्ति प्रतिदिन कैलरी (x) लेते है और उसका वजन (y) है । उस पर से क्रमांक सहसम्बन्ध गुणांक 0.6 मिलता है । बाद में जाँच करने पर पता चला कि एक व्यक्ति x और y चलों के क्रमों के बीच का अंतर 4 के बदले 2 लिया गया था, तो क्रमांक सह-सम्बन्ध की सही किमत ज्ञात करो ।
उत्तर :
यहाँ n = 10, r = 0.6 क्रमांक सह-सम्बन्ध दिया है, दो क्रमों के बीच का अंतर 4 के स्थान पर 2 लिया गया था । अर्थात् d = 4 सही के स्थान पर d = 2 गलत लिया गया । प्रथम Σd² ज्ञात करेंगे ।
∴ r = 1 – \(\frac{6 \sum \mathrm{d}^2}{\mathrm{n}\left(\mathrm{n}^2-1\right)}\)
0.6 = 1 – \(\frac{6 \sum d^2}{10\left(10^2-1\right)}\)
0.6 – 1 = \(\frac{6 \sum d^2}{10 \times 99}\)
-0.4 × 990 = -6Σd²
\(\frac{396}{6}\) = Σd²
Σd² = 66
सही Σd² = 66 + (4)² – (2)²
= 66 + 16 -4
∴ Σd² = 78
∴ r = 1 – \(\frac{6 \times 78}{10\left(10^2-1\right)}\)
= 1 – \(\frac{468}{10 \times 99}\)
= 1 – \(\frac{468}{990}\)
= 1 – 0.47
= 0.53
सही ∴ r = 0.53

प्रश्न 12.
10 व्यक्तियों का स्वास्थ्य का अंक (Health index) x और अपेक्षित आयु (Life expectancy) y के लिए सूचना प्राप्त की गई है । क्रमांक सह-सम्बन्ध गुणांक ज्ञात करने के लिए यह सूचना को क्रमांक दी गई और सभी क्रम के अंतर के वर्गों का योग 42.5 प्राप्त होता है । स्वास्थ्य अंक में 70 तीन बार और अपेक्षित आयु 45 दो बार पुनरावर्तित होता है, तो उस सूचना पर से कोटि सह-सम्बन्ध गुणांक ज्ञात करो।
उत्तर :
यहाँ n = 10, Σd² = 42.5 दिया है, 70 का तीन बार और 45 का दो बार पुनरावर्तन होता है । इसलिए ‘CF’ ज्ञात करेंगे । ‘CF’ निम्नानुसार सारणी बनाकर ज्ञात करेंगे ।

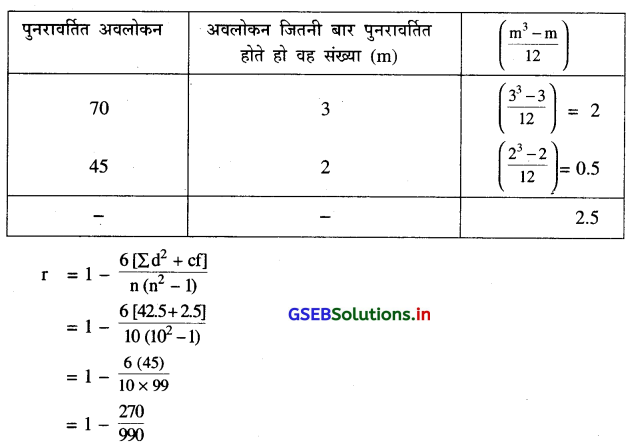
1 – 0.27
r = 0.73
∴ r = 0.73