Gujarat Board Statistics Class 12 GSEB Solutions Part 2 Chapter 2 Random Variable and Discrete Probability Distribution Ex 2.1 Textbook Exercise Questions and Answers.
Gujarat Board Textbook Solutions Class 12 Statistics Part 2 Chapter 2 Random Variable and Discrete Probability Distribution Ex 2.1
Question 1.
Examine whether the following distribution is a probability distribution of a discrete random variable X :
PM = \(\frac{x+2}{25}\); x = 1, 2, 3, 4, 5
Answer:
Here, p (x) = \(\frac{x+2}{25}\)
Putting, x = 1, 2, 3, 4, 5
P(1) = \(\frac{1+2}{25}\) = \(\frac{3}{25}\)
P(2) = \(\frac{2+2}{25}\) = \(\frac{4}{25}\)
P(3) = \(\frac{3+2}{25}\) = \(\frac{5}{25}\)
P(4) = \(\frac{4+2}{25}\) = \(\frac{6}{25}\)
P(5) = \(\frac{5+2}{25}\) = \(\frac{7}{25}\)
Now, by the definition of discrete probability distribution, we must have
(1) p(x) > 0 and (2) Σp(x) = 1.
Now, p(xi) > 0 for (i = 1, 2, 3, 4, 5) and
Σp(xi) = p(1) + p(2) + p(3) + p(4) + p(5)
= \(\frac{3}{25}+\frac{4}{25}+\frac{5}{25}+\frac{6}{25}+\frac{7}{25}\) = 1
Thus, conditions of probability distribution of discrete random variable are satisfied. So the given distribution is a probability distribution of a discrete random variable X.

Question 2.
If the following distribution is a probability distribution of variable X, then find constant k.
P(x) = \(\frac{6-|x-7|}{k}\); x = 4, 5, 6, 7, 8, 9, 10
Answer:
Here, P(x) = \(\frac{6-|x-7|}{k}\)
Putting, x = 4, 5, 6, 7, 8, 9, 10
P(4) = \(\frac{6-|4-7|}{k}\) = \(\frac{3}{k}\)
P(5) = \(\frac{6-|5-7|}{k}\) = \(\frac{4}{k}\)
P(6) = \(\frac{6-|6-7|}{k}\) = \(\frac{5}{k}\)
P(7) = \(\frac{6-|7-7|}{k}\) = \(\frac{6}{k}\)
P(8) = \(\frac{6-|8-7|}{k}\) = \(\frac{5}{k}\)
P(9) = \(\frac{6-|9-7|}{k}\) = \(\frac{4}{k}\)
P(10) = \(\frac{6-|10-7|}{k}\) = \(\frac{3}{k}\)
Now, by condition of probability distribution,
we must have
Σp(x) = 1
∴ P(4) + p(5) + P(6) + P(7) + P(8) + p(9) + P(10) = 1
∴ \(\frac{3}{k}+\frac{4}{k}+\frac{5}{k}+\frac{6}{k}+\frac{5}{k}+\frac{4}{k}+\frac{3}{k}\)
∴ \(\frac{30}{k}\) = 1
∴ k = 30
Hence, the value of k obtained is 30.
Question 3.
The probability distribution of a random variable X is defined as follows: P(x) = \(\frac{k}{(x+1) !}\); x = 1, 2, 3 and k = constant Hence, find (i) constant k (ii) P(1 < x < 4).
Answer:
Here, P(x) = \(\frac{k}{(x+1) !}\)
Putting x = 1, 2, 3,
P(1) = \(\frac{k}{(1+1) !}\) = \(\frac{k}{2 !}\) = \(\frac{k}{2}\)
P(2) = \(\frac{k}{(2+1) !}\) = \(\frac{k}{3 !}\) = \(\frac{k}{6}\)
P(3) = \(\frac{k}{(3+1) !}\) = \(\frac{k}{4 !}\) = \(\frac{k}{24}\)
(i) Now, by condition of probability distribution.
we must have
p(x) = 1
∴ p(1) + p(2) + p(3) = 1
∴ \(\frac{k}{2}+\frac{k}{6}+\frac{k}{24}\) = 1
∴ \(\frac{12 k+4 k+k}{24}\) = 1
∴ \(\frac{17 k}{24}\) = 1
∴ k = \(\frac{24}{17}\)

(ii) Now, P(1 < x < 4) = P(2) + P(3)
= \(\frac{k}{6}+\frac{k}{24}\) = \(\frac{4 k+k}{24}\) = \(\frac{5 k}{24}\)
Putting, k = \(\frac{24}{17}\)
p(1 < x < 4) = \(\frac{5 \times 24}{24 \times 17}\) = \(\frac{5}{17}\)
Hence, (i) k = \(\frac{24}{17}\) (ii) P(1 < X < 4) = \(\frac{5}{17}\)
Question 4.
The probability distribution of a random variable X is as follows:
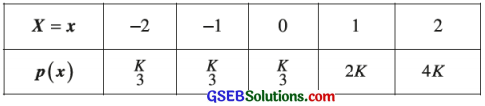
Then (i) Determine acceptable value of constant k. (ii) Find the mean of the distribution.
Answer:
(i) By condition of probability distribution, we must have
Σ p(x) = 1
∴ \(\frac{k}{3}+\frac{k}{3}+\frac{k}{3}\) + 2k + 4k2 = 1
∴ \(\frac{k+k+k+6 k+12 k^{2}}{3}\) = 1
∴ 9k + 12k2 = 3
∴ 12k2 + 9k – 3 = 0
∴ 3(4k2 + 3k – 1) = 0
∴ 4k2 + 4k – k – 1 = 0
∴ 4k (k+ 1) – 1(k + 1) = 0
∴ (4k- 1) (k + 1) = 0
∴ 4k – 1 = 0 or k + 1 = 0
∴ k = \(\frac{1}{4}\) or k = – 1
If k = – 1, then p(- 2) = – \(\frac{1}{3}\) which is not possible because p(x) > 0. So k = – 1 is not possible.
∴ Acceptable value is k = \(\frac{1}{4}\).
Putting k = \(\frac{1}{4}\), the probability distribution of random variable X is written as follows:
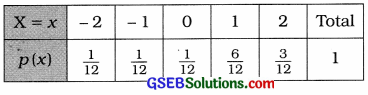
(ii) Mean of the distribution:
µ = Σx ∙ p(x)
= – 2\(\left(\frac{1}{12}\right)\) + – 1\(\left(\frac{1}{12}\right)\) + 0\(\left(\frac{1}{12}\right)\) + 1\(\left(\frac{6}{12}\right)\) + 2\(\left(\frac{3}{12}\right)\)
= \(\frac{-2-1+0+6+6}{12}\) = \(\frac{9}{12}\) = \(\frac{3}{4}\)
Hence, the acceptable value of constant k is \(\frac{1}{4}\) and the mean of the distribution obtained is \(\frac{3}{4}\).

Question 5.
The probability distribution of a random variable X is p (x). Variable X can assume the values x1 = – 2, x2 = – 1, x3 = 1 and x4 = 2 and if 4p(x1) = 2p (x2) = 3p (x3) = 4p (x4), then obtain mean and variance of this probability distribution.
Answer:
p(x) is the probability distribution of a random variable X.
X = x1; x2, x3, x4 and x1 = – 2, x2 = – 1, x3 = 1, x4 = 2.
Σp(x) = 1
∴ p (x1) + p(x2) + p(x3) + p(x4) = 1 ……………… (1)
Now, 4p(x1) = 2p(x2) = 3p(x3) = 4p(x4)
∴ 4p (x1) = 4p(x4), 2p(x2) = 4p (x4) and 3p(x3) = 4p (x4)
∴ p(x1) = p(x4), p(x2) = 2p (x4) and
P(x3) = \(\frac{4 p\left(x_{4}\right)}{3}\)
Putting these values in the result (1),
p (x4) + 2p (x4) + \(\frac{4 p\left(x_{4}\right)}{3}\) + p (x4) = 1
∴ \(\frac{3 p\left(x_{4}\right)+6 p\left(x_{4}\right)+4 p\left(x_{4}\right)+3 p\left(x_{4}\right)}{3}\) = 1
∴ 16p (x4) = 3
∴ p (x4) = \(\frac{3}{16}\)
Now, P(x1) = P(x4) = \(\frac{3}{16}\)
P(x1) = 2P(x4)
= 2 × \(\frac{3}{16}\)
= \(\frac{6}{16}\)
P(x3) = \(\frac{4 p\left(x_{4}\right)}{3}\)
= \(\frac{4 \times 3}{3 \times 16}\) = \(\frac{4}{16}\)
x1 = – 2, x2 = – 1, x3 = 1, and x4 = 2, the probability distribution of random variable X is written as follows:
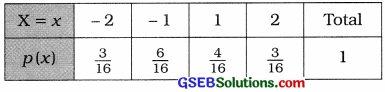
To find the mean and variance, the table is prepared as follows:
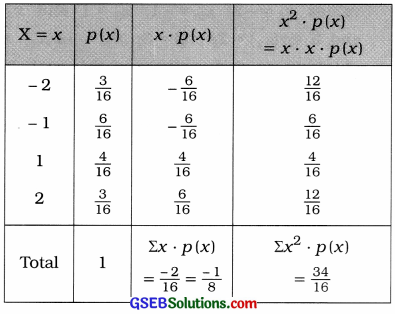
Mean of the distribution:
µ = E (X) = Σx ∙ p(x) = –\(\frac{1}{8}\)
Variance of the distribution:
σ2 = V(X) = E (X2) – [E (X)]2
= Σx2 ∙ p(x) – [Σx – p(x)]2
= \(\frac{34}{16}-\left(-\frac{1}{8}\right)^{2}\)
= \(\frac{34}{16}-\frac{1}{64}\)
= \(\frac{136-1}{64}\) = \(\frac{135}{64}\)
Hence, the mean and variance of the distribution obtained are \(\frac{1}{8}\) and \(\frac{135}{64}\) respectively.

Question 6.
A die is randomly tossed two times. Determine the probability distribution of the sum of the numbers appearing both the times on the die and obtain expected value of the sum.
Answer:
A die is randomly tossed two times.
∴ Total number of outcomes in the sample space U is n = 62 = 36.
For the sum of the numbers appearing both the times on the die is expressed as X = (u + v), where (u, v) is the element of U.
Now, the probability distribution X is obtained as shown in the following table:
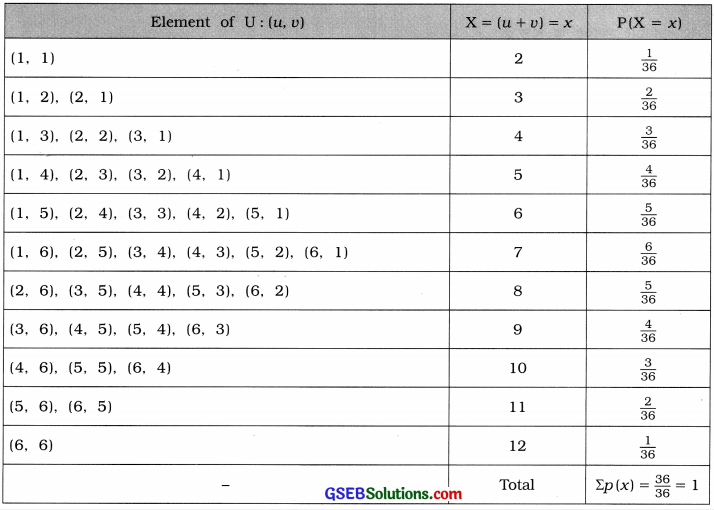
The probability distribution of X is written as follows:

Expected value of the sum:
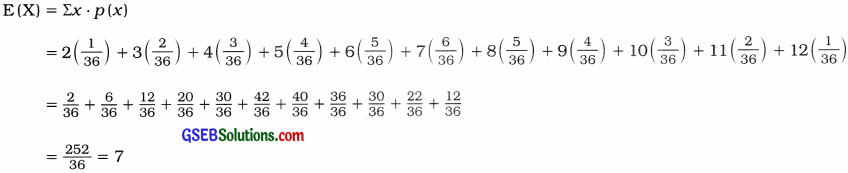
Hence, the expected value of the sum obtained is 7.
Alternative method:

Expected value of the sum:
E(X) = Σx ∙ p(x) = \(\frac{252}{36}\) = 7

Question 7.
A box contains 4 red and 2 blue balls. Three balls are simultaneously drawn at random. If X denotes the number of red bails in the selected balls, find the probability distribution of X and find the expected number of red balls in the selected balls.
Answer:
In a box total (4 red + 2 blue) 6 balls.
3 balls are simultaneously drawn at random.
∴ Total number of primary outcomes n = 6C3 = \(\frac{6 \times 5 \times 4}{3 \times 2 \times 1}\) = 20
X = No. of red balls in 3 balls drawn.
There are 4 red balls in a box.
∴ X = 0, 1, 2, 3.
The probability distribution of X is obtained as follows:

Expected value of red balls:
E(X) = Σx ∙ p(x)
= 2
Hence, the expected value of red balls obtained is 2 balls.
Question 8.
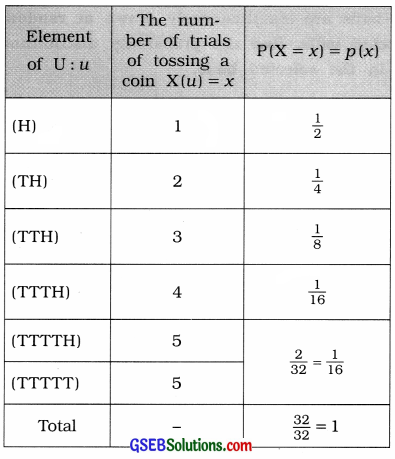
A coin is tossed till either a head or 5 tails are obtained. If a random variable X denotes the necessary number of trials of tossing the coin, then obtain probability distribution of the random variable X and calculate its mean and variance.
Answer:
A coin is tossed till either a head or 5 tails are obtained.
Suppose, X = Number of trials required for tossing a coin.
Here,
U = {(H), (TH), (TTH), (TTTH), (TTTTH), (TTTTT)}
∴ X = 1, 2, 3, 4, 5, 5
The following table shows the probability distribution of X:
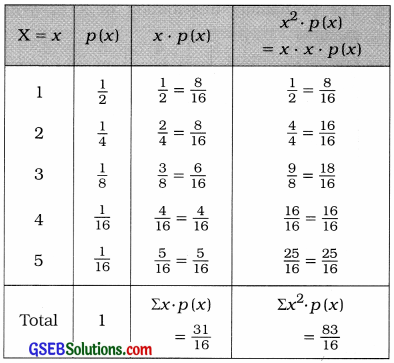
To find the mean and variance of the distribution, the following table is prepared:
Mean of the distribution:
µ = E(X)
= Σx ∙ p(x) = \(\frac{31}{16}\)
Variance of the distribution:
σ2 = V(X) = E(X2) – [E(X)]2
= Σx2 ∙ p(x) ∙ [Σx ∙ p(x)]2
= \(\frac{83}{16}-\left(\frac{31}{16}\right)^{2}\)
= \(\frac{83}{16}-\frac{961}{256}\)
= \(\frac{1328-961}{256}\) = \(\frac{367}{256}\)
Hence, the mean and variance of the distribution obtained are \(\frac{31}{16}\) and \(\frac{367}{256}\) respectively.

Question 9.
A shopkeeper has 6 tickets in a box. 2 tickets among them are worth a prize of ₹ 10 and the remaining tickets are worth a prize of ₹ 5. If a ticket is drawn at random from the box, find the expected value of the prize.
Answer:
In a box there are total 6 tickets of which 2 tickets are with a prize of ₹ 10 and 4 tickets are with a prize of ₹ 5.
One ticket is drawn at random.
∴ Total number of primary outcomes n = 6C1 = 6
X = The value of prize
= 5, 10
The probability distribution of X is obtained as follows:

The expected value of the prize:
E(X) = Σx ∙ P(x)
= \(\frac{40}{6}\)
= ₹ \(\frac{20}{3}\)
Hence, the expected value of the prize obtained is ₹ \(\frac{20}{3}\)