GSEB Solutions Class 12 Statistics Part 2 Chapter 5 विकलन Ex 5

Gujarat Board Statistics Class 12 GSEB Solutions Part 2 Chapter 5 विकलन Ex 5 Textbook Exercise Questions and Answers.

Gujarat Board Textbook Solutions Class 12 Statistics Part 2 Chapter 5 विकलन Ex 5

विभाग – A

निम्न विकल्प में से सही विकल्प चयन करके लिखिए ।

प्रश्न 1.
फलन f(x) का विकलित सूत्र कौन-सा है ?

उत्तर :

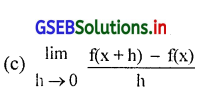
प्रश्न 2.
y = axⁿ, जहाँ a अचल संख्या हो, तो \(\frac{\mathrm{dy}{\mathrm{dx}}\) का मूल्य क्या होगा?
(a) nx^{n – 1}
(b) anx^{n – 1}
(c) 0
(d) anx^{n – 1}
उत्तर :
(b) anx^{n – 1}

प्रश्न 3.
y = ax + b, जहाँ a और b अचल संख्या हो, तो \(\frac{\mathrm{dy}{\mathrm{dx}}\) क्या होगा?
(a) a
(b) b
(c) a + b
(d) 0
उत्तर :
(a) a

प्रश्न 4.
f(x) = \(\frac{4}{x^2}\) का विकलित क्या होगा?
(a) \(\frac{4}{2 x}\)
(b) \(-\frac{8}{x^3}\)
(c) \(\frac{8}{\mathrm{x}^3}\)
(d) 0
उत्तर :
(b) \(-\frac{8}{x^3}\)

प्रश्न 5.
दो फलन u और v, x के फलन हो, तो उसका गुणाकार का विकलित का सूत्र क्या है ?

उत्तर :

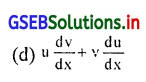
प्रश्न 6.
u और ,v x के पत्नन हो, तो \(\frac{\mathrm{v}}{\mathrm{u}}\) का विकलित सूत्र क्या है ?

उत्तर :

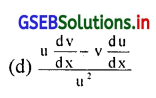
प्रश्न 7.
x = a आगे फलन बढ़ता हो, तो निम्न में से सही विकल्प क्या है?
(a) f’ (a) < 0 (b) f'(a) > 0
(c) f'(a) = 0
(d) f”(a) > 0
उत्तर :
(b) f'(a) > 0

प्रश्न 8.
किसी एक फलन x = a आगे न्यूनतम होने की आवश्यक और पर्याप्त शर्ते कौन-सी है?
(a) f'(a) = 0, f”(a) < 0 (b) f'(a) > 0, f”(a) > 0
(c) f'(a) = 0, f”(a) > 0
(d) f'(a) < 0, f”(a) > 0
उत्तर :
(c) f'(a) = 0, f”(a) > 0

प्रश्न 9.
मांग की मूल्य सापेक्षता का सूत्र कौन-सा है ?
(a) –\(\frac{p}{x} \cdot \frac{d x}{d p}\)
(b) \(\frac{p}{x} \cdot \frac{d x}{d p}\)
(c) –\(\frac{x}{p} \cdot \frac{d p}{d x}\)
(d) –\(\frac{p}{x} \cdot \frac{d p}{d x}\)
उत्तर :
(a) –\(\frac{p}{x} \cdot \frac{d x}{d p}\)

प्रश्न 10.
आमदानी फलन R दो महत्तम बनाने की शर्ते कौन-सी है?

उत्तर :

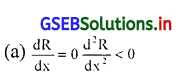
विभाग – B

निम्न प्रश्नों के उत्तर एक वाक्य में दीजिए ।

प्रश्न 1.
विकलन की परिभापा दीजिए।
उत्तर :
गाना कि f: A → R और a ∈ A, जहाँ A और R को किसी विवृत्त अंतराल है यदि \(\lim _{h \rightarrow 0} \frac{f(a+h)-f(a)}{h}\) का अस्तित्व हो, तो यह लक्ष को फलन f को a आगे का विकलित अथवा विकलन फल कहते है, उसे संकेत में f'(a) से दर्शाया जाता है।

प्रश्न 2.
फलन f(x) = 50 हो, तो f’ (x) ज्ञात कीजिए।
उत्तर :
यदि f(x)= 50 हो, तो f’ (x) = 0 होगा।

प्रश्न 3.
y = aⁿ, a अचल संख्या हो, तो \(\frac{d y}{d x}\) ज्ञात कजिए।
उत्तर :
यदि = aⁿ, a अचल संख्या हो, तो \(\frac{d y}{d x}\) = 0ⁿ = 0 होगा।

प्रश्न 4.
x के दो फलन का गुणाकार का कार्यनियम बताइए।
उत्तर :
यदि y = u.v हो, तो \(\frac{d y}{d x}\) = u\(\frac{d v}{d x}\) + v.\(\frac{d u}{d x}\) होगा।

प्रश्न 5.
यदि x = a आगे फलन घटता हो, तो x = a आगे फलन का प्रथम विकलित कैसा होगा?
उत्तर :
यदि x = a आगे फलन घटना हो, तो f”(a) < 0 होगा अर्थात् द्वितीय विकलित ऋण होगा।

प्रश्न 6.
किसी एक फलन x = a आगे महत्तम हो, तो x = a आगे फलन का द्वितीय कैसा होगा?
उत्तर :
यदि x = a आगे महत्तम हो, तो f”(x)<0 होगा अर्थात् द्वितीय विकलन ऋण होगा।

प्रश्न 7.
फलन के स्थिर बिंदु किसे कहते है?
उत्तर :
यदि बिंदु f(x) का महत्तम या न्यूनतम मूल्य प्राप्त होता है उसे स्थिर बिंदुओं कहते है। \(\frac{d y}{d x}\) = 0 का समाधान करती x के मूल्यों प्राप्त कीजिए स्थिर बिंदुओं कहते है।

प्रश्न 8.
सीमांत आमदानी किसे कहते है?
उत्तर :
माँग में अल्प परिवर्तन होने से आमदानी में होते परिवर्तन को सीमांत आमदानी कहते है। सीमांत आमदानी = \(\frac{d R}{d x}\)

प्रश्न 9.
सीमांत खर्च की परिभाषा दीजिए।
उत्तर :
उत्पादन में अल्प परिवर्तन करने से होते परिवर्तन को सीमांत खर्च कहते है। सीमांत खर्च = \(\frac{d c}{d x}\)

प्रश्न 10.
माँग की मूल्य सापेक्षता का सूत्र बताइए।
उत्तर :
माँग की मूल्य सापेक्षता = –\(\frac{\mathrm{P}}{\mathrm{x}} \cdot \frac{\mathrm{dx}}{\mathrm{dp}}\)

प्रश्न 11.
f(x) = 7x² – 6x + 5 हो, तो f’ (x) प्राप्त कीजिए।
उत्तर :
यहाँ f(x) = 7x² – 6x + 5
∴ f’ (x) = 14x – 6

प्रश्न 12.
y = 6x³ + \(\frac {7}{2}\)x² + \(\frac {6}{5}\)x – 8 हो, तो \(\frac{\mathrm{dy}}{\mathrm{dx}}\) प्राप्त कीजिए।
उत्तर :
यहाँ y = 6x³ + \(\frac {7}{2}\)x² + \(\frac {6}{5}\)x – 8
∴\(\frac{\mathrm{dy}}{\mathrm{dx}}\) = 18x² + 7x + \(\frac {6}{5}\)

विभाग – C

निम्न प्रश्नों के उत्तर दीजिए ।

प्रश्न 1.
विकलित की परिभाषा दीजिए।
उत्तर :
जब हम x = a लेंगे तब f(x) का मूल्य f(a) होगा। जब x के मूल्य में अल्प वृद्धि करके a से a + h किया जाये तो परिणाम फलन का मूल्य
f(a) से f(a + h) होगा x के मूल्य में (a + h) – a = h का परिवर्तन होगा तब f(x) की किंमत में f(a + h) – f(a) का परिवर्तन होगा। a के मूल्य में जितना परिवर्तन करने से फलन के मूल्य में हुआ सापेक्ष परिवर्तन यदि अल्प किया जाये तो ऐसे सापेक्ष परिवर्तन के लक्ष्य को f(x) का ‘a’ के आगे का विकलित कहते है।

प्रश्न 2.
विकलन का भागाकार का नियम बताइए।
उत्तर :

प्रश्न 3.
किसी एक फलन x = a के आगे महत्तम होने की आवश्यक और पर्याप्त शतें बताइए।
उत्तर :
किसी एक फलन x = a आगे महत्तम होने के लिए निम्न शर्ते आवश्यक और पर्याप्त है।
(i) f (a) = 0
(ii) f'(a) < 0

प्रश्न 4.
सीमांत खर्च समझाइए और उसका सूत्र दीजिए।
उत्तर :
वस्तु के x इकाई उत्पादन करने के खर्च c से दर्शाया जाय तो c को भी x का फलन के रूप में प्रस्तुत किया जा सकता है। उत्पादन में अल्प
परिवर्तन करने से खर्च में होते परिवर्तन को सीमान्त खर्च (Marginal Cost) कहते है। खर्च का फलन का x सापेक्ष विकलित लेने से सीमान्त खर्च प्राप्त किया जाता है। इस प्रकार उत्पादन x हो तब सीमांत खर्च = \(\frac{\mathrm{dc}}{\mathrm{dx}}\)

प्रश्न 5.
मांग की मूल्य सापेक्षता की परिभाषा दीजिए।
उत्तर :
माँग में होते प्रतिशत परिवर्तन और मूल्य में होता परिवर्तन के अनुपात को मांग की मूल्य सापेक्षता कहते है। अर्थात्

प्रश्न 6.
लाभ का फलन P को महत्तम बनाने की कौन-सी शर्ते है ?
उत्तर :
लाभ का फलन P को न्यूनतम बनाने की शर्ते
(i) \(\frac{\mathrm{dp}}{\mathrm{dx}}\) = 0 और
(ii) \(\frac{\mathrm{d}^2 \mathrm{p}}{\mathrm{dx}}\) < 0

प्रश्न 7.
उत्पादन खर्च का फलन C को न्यूनतम बनाने की शर्ते बताइए।
उत्तर :
उत्पादन खर्च का फलन C को न्यूनतम बनाने की शर्ते
(i) \(\frac{\mathrm{dp}}{\mathrm{dx}}\) = 0 और
(ii) \(\frac{\mathrm{d}^2 \mathrm{c}}{\mathrm{dx}^2}\)> 0

प्रश्न 8.
यदि f(x) = \(\sqrt[4]{x}\) हो, तो f”(x) ज्ञात कीजिए।
उत्तर :

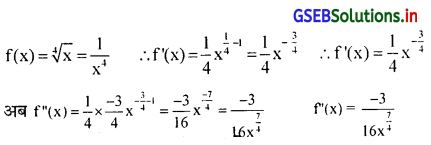
प्रश्न 9.
विकलन के श्रृंखला नियम’ को लिखिए।
उत्तर :
श्रृंखला का नियम \(\frac{d y}{d x}=\frac{d y}{d u} \times \frac{d u}{d x}\) (y यह u का फलन और u यह x का फलन हो, तब)

प्रश्न 10.
f(x) = x⁴ – 4x³ + 3x² + x + 1 के लिए f”(0) प्राप्त कीजिए।
उत्तर :
f(x) = x⁴ – 4x³ + 3x² + x + 1
f’ (x) = 4x³ – 12x² + 6x + 1 + 0 f”(x) = 12x² – 24x + 6
f”(0) = 12(0)² + 24(0) +6 = 0 + 0 + 6 ∴ f”(0) = 6

प्रश्न 11.
आमदानी फलन 90x – \(\frac{x^2}{2}\) हो, तो सीमांत आमदानी ज्ञात कीजिए।
उत्तर :
सीमांत आमदानी \(\frac{\mathrm{dR}}{\mathrm{dx}}\) = 90x – \(\frac{x^2}{2}\) 90 – \(\frac{2 x}{2}\) 90 – x सीमांत आमदानी = 90 – x

प्रश्न 12.
फलन का महत्तम मूल्य अर्थात् क्या?
उत्तर :
x = a आगे फलन का मूल्य y = f(a) होगा। यदि h अल्प धन संख्या हो और यदि f(a) > f(a + h) और f(a) > f(a – h) हो, तो x = a समक्ष फलन महत्तम है ऐसा कहते है।

प्रश्न 13.
फलन किसी एक बिंदु समक्ष घटता है ऐसा कब कहा जाता है?
उत्तर :
x = a आगे फलन का मूल्यy = f(a) होता है। यदि h अल्प धन संख्या हो और यदि f(a + h) < f(a) और f(a) < f(a – h) हो, तो x = a आगे f(x) यह घटता फलन है ऐसा कहते है।

प्रश्न 14.
फलन y = 12 + 4x – 7x², x = 2 समक्ष फलन बढ़ता या घटता होता है वह निश्चित कीजिए।
उत्तर :
y = 12 + 4x – 7x² ∴ \(\frac{d y}{d x}\) = 0 + 4 – 14x ∴ \(\frac{d y}{d x}\) = 4 – 14x x = 2 आगे
\(\frac{d y}{d x}\) = 4 – 14(2) = 4 – 28 = -24 = -24 < 0 ∴ x = 2 आगे फलन घटता होता है।

प्रश्न 15.
y = 4x² + 4x + 8 का विकलित ज्ञात कीजिए। x की कौन-सी किंमत के लिए यह विकलित शून्य बनता है वह ज्ञात कीजिए।
उत्तर :
y = 4x² + 4x + 8 f’ (x) = 8x + 4 + 0 = 8x + 4 अब f”(x) = 0 दिया है।
∴ 8x + 4 = 0 ∴ 8x = -4 ∴ x = \(\frac{-4}{8}\) ∴ x = \(\frac{-1}{2}\) ∴ x = \(\frac{-1}{2}\) हो, तो विकलित शून्य ‘0’ बनता है।

प्रश्न 16.
सिद्ध कीजिए कि f(x) = x³ + 5x² + 3x + 7 के लिए f'(2) = 35 होगा।
उत्तर :
f(x) = x³ + 5x² + 3x + 7 f'(x) = 3x² + 10x + 3 + 0 f'(x)= 3x² + 10x +3 x = 2 दिया है।
f'(2)= 3(2)² + 10(2) + 3 = 3 × 4 + 20 + 3 = 12 + 20 + 3 f'(2)= 35 ∴ f(2)= 35 प्राप्त होता है।

प्रश्न 17.
यदि f(x) = 3x² + 3 हो, तो x की कौन-सी किंमत के लिए f'(x) = f(x) होगा?
उत्तर :
f(x) = 3x² + 3 f(x) = 6x +0 ∴ f’ (x) = 6x
अब f”(x) = f(x) में f'(x) = 6x और f(x) = 3x² + 3 रखने पर
6x = 3x² + 3 3x² – 6x + 3 = 0 ∴ 3(x² – 2x + 1 = 0)
∴ x² – 2x + 1 = 0 (x – 1) (x – 1) = 0
x = 1 अथवा x = 1 x = 1 हो तब f'(x) = f(x) होगा।

प्रश्न 18.
यदि y = 2x³ + 5x² – 3 + \(\frac{4}{x^2}-\frac{5}{x^3}\) हो, तो \(\frac{d^2 y}{d x^2}\) ज्ञात कीजिए।
उत्तर :

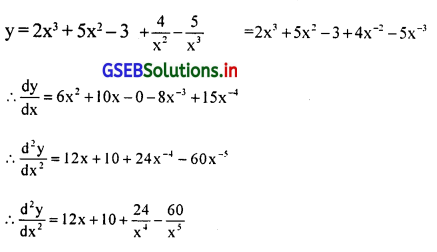
प्रश्न 19.
यदि y = \(\sqrt{x}+\frac{1}{\sqrt{x}}\) हो, तो \(\frac{\mathrm{d}^2 \mathrm{y}}{\mathrm{d} \mathrm{x}^2}\) ज्ञात कीजिए।
उत्तर:

प्रश्न 20.
प्रति इकाई उत्पादन खर्च का फलन C = 0.0012x² – 0.18x + 25 हो, तो सीमांत खर्च प्राप्त कीजिए।
उत्तरः
उत्पादन खर्च का फलन C = 0.0012x² – 0.18x + 25
∴ सीमांत खर्च \(\frac{\mathrm{dc}}{\mathrm{dx}}\) = 0.0024x – 0.18 + 0 ∴ \(\frac{\mathrm{dc}}{\mathrm{dx}}\) = 0.0024x – 0.18

विभाग – D

निम्न प्रश्नों के उत्तर दीजिए ।

प्रश्न 1.
परिभाषा की सहायता से y = ax + b(a और b अचल संख्या है) का विकलित ज्ञात कीजिए।
उत्तर :
यहाँ y = ax + b

इसलिए y = ax + b हो, तो \(\frac{d y}{d x}\) = a

प्रश्न 2.
परिभाषा की सहायता से f(x) = x¹⁰ का विकलित प्राप्त कीजिए।
उत्तर :
यहाँ f(x) = x¹⁰ ∴ f(x + h)= (x + h)¹⁰

= 10x^{10 – 1}
= 10x⁹
यदि x¹⁰ हो, तो f'(x) = 10x⁹

प्रश्न 3.
परिभाषा की सहायता से f(x) = \(\frac{2}{3+4 x}\) का विकलित प्राप्त कीजिए।
उत्तर :

प्रश्न 4.
y = x³ – 3x² – 3x + 80 फलन के लिए x की कौन-सी किंमत के लिए \(\frac{d y}{d x}\) = -6 होगा?
उत्तर :
y = x³ – 3x – 3x + 80 \(\frac{d y}{d x}\) = 3x – 6x – 3 + 0
∴ \(\frac{d y}{d x}\) = 3x² – 6x – 3 \(\frac{d y}{d x}\) = -6 दिया है। ∴ -6 = 3x² – 6x – 3 3x² – 6x – 3 + 6= 0
3x² – 6x + 3 = 0 3(x² – 2x + 1) = 0 ∴ x² – 2x + 1 = 0 x² – x – x + 1 = 0_x(x – 1)-1(x – 1) = 0
∴ x – 1 = 0 अथवा x – 1 = 0 ∴ x = 1
x = 1 हो तब \(\frac{d y}{d x}\) = -6 होगा।

प्रश्न 5.
यदि f(x) = \(\frac{4 x^5+3 x^3+2 x^2+24}{x^2}\) हो, तो f'(2) ज्ञात कीजिए।
उत्तर:
f(x) = \(\frac{4 x^5+3 x^3+2 x^2+24}{x^2}\) = \(\frac{4 x^5}{x^2}+\frac{3 x^3}{x^2}+\frac{2 x^2}{x^2}+\frac{24}{x^2}\) = 4x³ + 3x + 2 + 24(x)^-2
f’ (x) = 12x + 3 + 0 – 48x^-3 = 12x² + 3 – 48x^-3 ∴ = 12x² + 3\(\frac{-48}{x^3}\)
x = 2 रखने पर ∴ 48 + 3 – 6
f(2) = 12(2)² + 3 – \(\frac{48}{(2)^3}\) = 12 × 4 + 3 – \(\frac{48}{8}\) = 48 + 3 – 6 = 51 – 6 = 45 f'(2)= 45 होगा।

प्रश्न 6.
y = (3x² + 4x – 2) (3x + 2) का x के सापेक्ष अविकलित प्राप्त कीजिए।
उत्तर :
y = (3x² + 4x – 2) (3x + 2)
यहाँ u = 3x² + 4x – 2 v = 3x + 2 लिजिए ।
∴ \(\frac{\mathrm{du}}{\mathrm{dx}}\) = 6x + 4 और \(\frac{\mathrm{dv}}{\mathrm{dx}}\) = 3
अब y = u.v है।
∴ \(\frac{\mathrm{dy}}{\mathrm{dx}}\) = u\(\frac{\mathrm{dv}}{\mathrm{dx}}\) + v\(\frac{\mathrm{du}}{\mathrm{dx}}\)
(3x² + 4x – 2)(3)+ (3x + 2)(6x + 4)
= 9x² + 12x – 6+ 18x² + 12x + 12x +8
= 27x² + 36x + 2
∴ \(\frac{\mathrm{dy}}{\mathrm{dx}}\) = 27x² + 36x + 2

प्रश्न 7.
y = \(\frac{\mathrm{ax}+\mathrm{b}}{\mathrm{bx}+\mathrm{a}}\) (a और b अचल संख्या है) तो \(\frac{d y}{d x}\) ज्ञात कीजिए।
उत्तर :
यहाँ y = \(\frac{\mathrm{ax}+\mathrm{b}}{\mathrm{bx}+\mathrm{a}}\) मानाकि u = ax + b
∴ \(\frac{d u}{d x}\) = a(i) + 0 = a और v = bx + a
∴ \(\frac{d v}{d x}\) = b(1) + 0 = b अब y = \(\frac{\mathrm{u}}{\mathrm{v}}\)

प्रश्न 8.
y = 1 + \(\frac{1}{1+\frac{1}{x}}\) का x के सापेक्ष विकलित ज्ञात कीजिए।
उत्तर :

प्रश्न 9.
(2x + 3) (y + 2 ) = 15 हो, तो \(\frac{\mathrm{dy}}{\mathrm{dx}}\) ज्ञात कीजिए।
उत्तर :
(2x + 3) (y + 2) = 15 2xy + 4x + 3y + 6 = 15 2xy + 3y = 15 – 6 – 4x y(2x + 3)= 9 – 4x
∴ y = \(\frac{9-4 x}{2 x+3}\) u = 9 – 4x और v = 2x + 3

प्रश्न 10.
यदि y = 5 + \(\frac{6}{7 x+8}\) हो, तो \(\frac{\mathrm{dy}}{\mathrm{dx}}\) ज्ञात कीजिए।
उत्तर :

प्रश्न 11.
यदि f(x) = \(\sqrt{x^2+5}\) हो, तो f'(x) ज्ञात कीजिए।
उत्तर :

प्रश्न 12.
\(\left(3 x^3-2 x^2+1\right)^{\frac{5}{2}}\) का x के सापेक्ष विकलित ज्ञात कीजिए।
उत्तर :

प्रश्न 13.
f(x) = (x² + 3x + 4)⁷ हो, तो f'(x) ज्ञात कीजिए।
उत्तर :
f(x) = (x² + 3x + 1)⁷
u = x² + 3x + 1 y = u⁷
∴ \(\frac{d u}{d x}\) 2x + 3 \(\frac{d y}{d x}\) 7u⁶
अब \(\frac{d y}{d x}=\frac{d y}{d u} \times \frac{d u}{d x}\) = (7u⁶)(2x + 3) u का मूल्य रखने पर
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) = 7(x² + 3x + 4)⁶ (2x + 3) f'(x) = 7(x² + 3x + 4)⁶ (2x + 3)

प्रश्न 14.
यदि f(x) = 3x² + 4x + 5 हो, तोx की कौन-सी किंमत के लिए f'(x) =f'(x) होगा?
उत्तर :
f(x) = 3x² + 4x + 5
f'(x) = 6x + 4
अब f”(x) = 6
f'(x) = f”(x)
∴ 6x + 4 = 6 6x = 6 – 4 6x = 2 x = \(\frac {2}{6}\) = \(\frac {1}{3}\)
x = \(\frac {1}{3}\) हो तब f”(x) = f”(x) होगा।

प्रश्न 15.
यदि मांग का फलन P = \(\frac{2500-x^2}{100}\) हो, तो सीमांत आमदानी ज्ञात कीजिए।
उत्तर :
यदि माँग का फलन P = \(\frac{2500-x^2}{100}\)
∴ आमदानी फलन R = P.x (\(\frac{2500-x^2}{100}\))x
∴ R = \(\frac{2500 x-x^3}{100}=\frac{2500 x}{100}-\frac{x^3}{100}\) 25x – \(\frac{x^3}{100}\)
सीमांत आमदानी \(\frac{\mathrm{dR}}{\mathrm{dx}}\) = 25 – \(\frac{3 x^2}{100}\)

प्रश्न 16.
यदि y = 3x² – 10x + 7 हो, तो x = 1 और x = 2 आगे फलन बढ़ता है या घटता है, यह निश्चित कीजिए।
उत्तर :
y = 3x² – 10x + 7 ∴ \(\frac{d y}{d x}\) = 6x – 10 _x = 1 आगे
\(\frac{d y}{d x}\) = 6(1) – 10 = 6 – 10 = -4 < 0 ∴ x = 1 आगे फलन घटता है। x = 2 आगे \(\frac{d y}{d x}\) = 6(2) – 10 = 12 – 10 = 2 > 0
∴ x = 2 आगे फलन बढ़ता है।

प्रश्न 17.
यदि y = 2x³ – 7x² – 11x + 5 हो, तो x = \(\frac {1}{2}\) और x = 3 आगे फलन बढ़ता है या घटता है, यह निश्चित कीजिए।
उत्तरः
y = 2x³ – 7x² – 11x + 5
∴ \(\frac{d y}{d x}\) = 6x² – 14x – 11
अब x = \(\frac {1}{2}\) आगे
\(\frac{d y}{d x}\) = 6(\(\frac {1}{2}\))² – 14 × \(\frac {1}{2}\) – 11
= 6 × \(\frac {1}{4}\) – 7 – 11 = \(\frac {3}{2}\) – 18
= \(\frac{-33}{2}\) < 0
∴ x = \(\frac {1}{2}\) आगे फलन घटता है। x = 3 आगे
\(\frac{d y}{d x}\) = 6 × (3)² -14(3) – 11 = 6 × 9 – 42 – 11 = 54 – 53 = 1 > 0
∴ x = 3 आगे फलन बढ़ता है।

प्रश्न 18.
फलन y = 3 + 2x -7x² x = -4 और x = 4 आगे फलन बढ़ता है या घटता है, यह निश्चित कीजिए।
उत्तरः
y = 3 + 2x – 7x²
∴ \(\frac{d y}{d x}\) = 0 + 2 – 14x \(\frac{d y}{d x}\) = 2 – 14x
अब x = 4 आगे = 2 – 14 (-4) =2 + 56 = 58 > 0
∴ x = -4 आगे फलन बढ़ता है।
x = 4 आगे
= 2 – 14(4)
= 2 – 56
= -54 < 0
∴ x = 4 आगे फलन घटता है।

प्रश्न 19.
चीनी के कारखाने का उत्पादन खर्च C = \(\frac{x^2}{10}\) + 5x + 200 है। यदि उत्पादन 100 इकाई हो, तो सीमान्त खर्च ज्ञात करो और उसका अर्थघटन कीजिए।
उत्तरः
उत्पादन खर्च का फलन C = \(\frac{x^2}{10}\) + 5x + 200
∴ सीमान्त खर्च \(\frac{\mathrm{dc}}{\mathrm{dx}}=\frac{2 \mathrm{x}}{10}\) + 5 = \(\frac{x}{5}\) + 5 जब x = 100 हो तब
सीमान्त खर्च \(\frac{d c}{d x}=\frac{100}{5}\) + 5 = 20 + 5 = 25
अर्थघटन : 101वीं इकाई उत्पादन करने का खर्च ₹ 25 होगा।

प्रश्न 20.
किसी वस्तु की x इकाई बनाने का खर्च का फलन C = 50 + 2x + √x हो, तो 100 इकाई के उत्पादन के लिए सीमांत खर्च ज्ञात कीजिए और उसका अर्थघटन कीजिए।
उत्तर :
खर्च का फलन C = 50 + 2x + √x
∴ सीमान्त खर्च \(\frac{d c}{d x}\) = 0 + 2 + \(\frac{1}{2} x^{\frac{-1}{2}}\)
∴ = \(\frac{d c}{d x}\) = 2 + \(\frac{1}{2 \sqrt{x}}\) जब x = 100 हो तब
∴ = \(\frac{d c}{d x}\) 2 + \(\frac{1}{2 \sqrt{100}}\)
= 2 + \(\frac{1}{2 \times 10}\)
= 2 + \(\frac{1}{20}\) = 0.05 = 2.05
अर्थघटन : 101वीं इकाई उत्पादन करने का खर्च ₹ 2.05 होगा।

प्रश्न 21.
फलन की महत्तम और न्यूनतम किंमते प्राप्त करने की विधि बताइए।
उत्तर :

1. दिया फलन के लिए \(\frac{d y}{d x}\) = f'(x) प्राप्त कीजिए।
2. समीकरण \(\frac{d y}{d x}\) = 0 का समाधान करती x की किंमत प्राप्त कीजिए, जिसे स्थिर बिंदु कहते है।
3. द्वितीय विकलन प्राप्त करके उसमें x की यह किमतें बारी बारी से रखिए।
4. जिस स्थिर बिंदु के लिए द्वितीय विकलित का मूल्य धन हो, x की उसे किंमत फलन की न्यूनतम किंमत देते है और जिस स्थिर बिंदु के लिए द्वितीय विकलित की किंमत ऋण होगी, x की उस किंमत फलन की महत्तम किंमत देती है।
5. फलन की महत्तम अथवा न्यूनतम किंमत प्राप्त करने के लिए उपर्युक्त x की किंमतें फलन में रखा जाता है।

विभाग – E

निम्न प्रश्नों के उत्तर दीजिए ।

प्रश्न 1.
विकलन के लिए कार्यनियम दीजिए। उत्तरः यहाँ x के दो फलन के योग, गुणाकार, भागाकार घटाव के लिए विकलित प्राप्त करने के लिए कुछ नियम सिद्ध किये बिना स्वीकार करें यदि u और v यह x के विकलनीय फलन हो, तो


नियम-4: (सांकड नियम) यदि y यह u का फलन और u यह x का फलन हो, तो = \(\frac{d y}{d x}=\frac{d y}{d u} \times \frac{d u}{d x}\)

प्रश्न 2.
फलन बढ़ता है या घटता है उसे विकलित के उपयोग करके कैसे निश्चित करोगे?
उत्तर :
x = a आगे फलन की किंमत y = f(a) हो, यदिh अल्प धन संख्या हो और यदि f(a + h) > f(a) एवं f(a) > (a – h) हो, तो x = a आगे f(x) यह बढ़ता फलन है ऐसा कहेंगे। x = a आगे फलन की किंमत y = f(a) हो, यदि h अल्प धन संख्या हो और यदि f(a + h) < f(a) एवं
f(a) < f(a – h) हो, तो x = a आगे f(x) यह घटता फलन है ऐसा कहेंगे।

प्रश्न 3.
फलन की महत्तम किंमत अर्थात् क्या ? महत्तम किंमत की शर्ते बताइए।
उत्तरः
x = a आगे फलन की किंमत y = f(a) हो, यदिh अल्प धन संख्या हो और यदि f(a) > f(a + h) एवं f(a) >(a – h) हो, तो x = a आगे फलन
महत्तम है ऐसा कहेंगे। किसी एक फलन x = a आगे महत्तम होने के लिए निम्न शर्ते पर्याप्त है :
(i) f'(a) = 0
(ii) f”(a) < 0

प्रश्न 4.
फलन की न्यूनतम किंमत अर्थात् क्या? न्यूनतम किंमत के लिए शर्ते बताइए। .
उत्तर :
x = a आगे फलन का मूल्य y = f(a) हो, यदि h अल्प धन संख्या हो और यदि f(a) < f(a + h) एवं f(a) < f(a – h) हो, तो x = a आगे फलन न्यूनतम है ऐसा कहेंगे। किसी एक फलन x = a आगे न्यूनतम होने के लिए निम्न शर्ते आवश्यक और पर्याप्त है : (i) f'(a) = 0 (ii) f”(a) > 0

प्रश्न 5.
एक कारखाने में प्रति सौ टन स्टील का उत्पादन खर्च \(\frac {1}{10}\)x³ – 4x² + 50x + 300 है।न्यूनतम खर्च के लिए उत्पादन निश्चित कीजिए।
उत्तर :
उत्पादन खर्च का फलन C = \(\frac {1}{10}\)x³ – 4x² + 50x + 300

∴ न्यूनतम खर्च के लिए उत्पादन खर्च \(\frac {50}{3}\) के लिए \(\frac {50}{3}\)

प्रश्न 6.
किसी माल की x इकाई तैयार करने का प्रति इकाई खर्च C = 1000 + 8x + \(\frac{5000}{x}\) हो, तो खर्च न्यूनतम हो इसके लिए उत्पादन कितना करना चाहिए? न्यूनतम खर्च भी ज्ञात कीजिए।
उत्तर :
प्रति इकाई खर्च का फलन C = 1000 + 8x + \(\frac{5000}{x}\)
∴ \(\frac{\mathrm{dc}}{\mathrm{dx}}\) = 0 + 8 + (-5000)x^-2
= 8 – \(\frac{5000}{x^2}\)
\(\frac{\mathrm{dc}}{\mathrm{dx}}\) = 0 रखने पर
∴ 8 – \(\frac{5000}{x^2}\) = 0
∴ 8x² – 5000 = 0
∴ x² = \(\frac{5000}{8}\)
∴ x² = 625 .∴ x = 25
अब \(\frac{\mathrm{d}^2 \mathrm{c}}{\mathrm{dx}^2}\) = 0 + 10000x^-3 = \(\frac{10000}{x^3}\) x = 25 रखने पर
\(\frac{\mathrm{d}^2 \mathrm{c}}{\mathrm{dx}^2}=\frac{10000}{(25)^3}=\frac{10000}{15625}\) = 0.64 > 0
∴ x = 25 के लिए उत्पादन खर्च न्यूनतम होगा। न्यूनतम खर्च ज्ञात करने के लिए x = 25 रखने पर
न्यूनतम खर्च = 1000 + 8(25) + \(\frac{5000}{25}\) = 1000 + 200 + 200 = 1400
न्यूनतम खर्च = 1400

प्रश्न 7.
एक वस्तुका प्रति इकाई उत्पादन खर्च का फलन C = 1500+ 0.05x – 2√x है। सिद्ध कीजिए कि उत्पादन 400 इकाई किया जाय
तब उत्पादन खर्च न्यूनतम होगा।
उत्तर :
उत्पादन खर्च का फलन C = 1500 + 0.05x – 2√x

400 इकाई ∴ x = 400 रखने पर \(\sqrt{400}\) = 20 20 = 20
LHS = RHS, 400 इकाई पर उत्पादन खर्च न्यूनतम होगा।

प्रश्न 8.
एक वस्तु की मांग का फलन P = 30 – \(\frac{x^2}{10}\) है। महत्तम आमदानी के लिए मांग और किंमत ज्ञात कीजिए।
उत्तर :
माँग की फलन P = 30 – \(\frac{x^2}{10}\)
आमदानी फलन R = p = (30 – \(\frac{x^2}{10}\))x
= 3x – \(\frac{x^3}{10}\)
\(\frac{\mathrm{dR}}{\mathrm{dx}}\) = 30 – \(\frac{3x^2}{10}\) \(\frac{\mathrm{dR}}{\mathrm{dx}}\) = 0
30 – \(\frac{3x^2}{10}\) = 0
300 – 3x² = 0
300 = 3x²
∴ \(\frac{300}{3}\) = x² > x² = 100
∴ x = \(\sqrt{100}\) ∴ x = 10
P = 30 – \(\frac{x^2}{10}\)
= 30 – \(\frac{(10)^2}{10}\)
= 30 – \(\frac{100}{10}\)
= 30 – 10 P = 20
माँग = 10 इकाई, किंमत = 20₹

प्रश्न 9.
बाजार में चावल की माँग x = 3 (60 – P) हो, तो महत्तम आमदानी के लिए मांग ज्ञात कीजिए और उस माँग के लिए किंमत और आमदानी प्राप्त कीजिए।
उत्तर :
माँग की फलन x = 3 (60-P)
x = 180 – 3P
3P = 180 – x


आमदानी फलन R = P.x = 30 × 90
∴ R = 2700
x = 90, P = 30, R = 2700

प्रश्न 10.
यदि माँग का फलन P = 75 – \(\frac{x^2}{2500}\) हो, तो कौन-सी माँग पर आमदानी महत्तम होगी ? महत्तम आमदानी के लिए किंमत भी ज्ञात
कीजिए।
उत्तर :

माँग = 250 इकाई, किंमत P = 50

प्रश्न 11.
एक उत्पादक का लाभ का फलन 40x + 1000 – 0.1x² है। कौन-से उत्पादन पर उसका लाभ महत्तम होगा? महत्तम लाभ ज्ञात
कीजिए।
उत्तर :
लाभ का फलन P = 40x + 10000 – 0.1x²
∴ \(\frac{\mathrm{dp}}{\mathrm{dx}}\) = 40 + 0 – 0.2x
∴ \(\frac{\mathrm{dp}}{\mathrm{dx}}\) = 40- 0.2x \(\frac{\mathrm{dp}}{\mathrm{dx}}\) = 0 रखने पर
0 = 40 – 0.2x 0.2x = 40 x = \(\frac{40}{0.2}\) ∴ x = 200
अब \(\frac{d^2 p}{d x^2}\) = 0 – 0.2x = -0.2 < 0 \(\frac{d^2 p}{d x^2}\) = -0.2 < 0
∴ x = 200 पर लाभ महत्तम होगा।
P = 40x + 10000 – 0.1x² में x = 200 रखने पर
=40(200) + 10000 – 0.1(200)²
= 8000 + 10000 – 0.1 (40000)
= 18000 – 4000
P = 14000 ∴ x = 200 और P= 14000

प्रश्न 12.
एक व्यापारी का लाभ का फलन 5x – 100 – 0.01x² है। महत्तम लाभ प्राप्त करने के लिए कितनी इकाई का उत्पादन करना
चाहिए?
उत्तर :
लाभ का फलन P = 5x – 100 – 0.01x²
∴ \(\frac{\mathrm{dp}}{\mathrm{dx}}\) = 5 – 0 – 0.02x ∴ \(\frac{\mathrm{dp}}{\mathrm{dx}}\) = 5 – 0.02x \(\frac{\mathrm{dp}}{\mathrm{dx}}\) = 0 रखने पर
0 = 5 – 0.02x 0.02x = 5
∴ x = \(\frac{5}{0.02}\) ∴ x = 250
महत्तम लाभ प्राप्त करने के लिए 250 इकाई का उत्पादन करना चाहिए।

विभाग – F

निम्न प्रश्नों के उत्तर दीजिए ।

प्रश्न 1.
y = 2x³ – 15x² + 36x + 12 हो, तो x की कौन-सी किंमत के लिएy महत्तम या न्यूनतम होगा? इसके महत्तम और न्यूनतम किंमत ज्ञात कीजिए।
उत्तर :
यहाँ y = 2x³ – 15x² + 36x + 12
∴ \(\frac{d y}{d x}\) = 6x² – 30x + 36
स्थिर किंमत के लिए \(\frac{d y}{d x}\) = 0
∴ 6x² – 30x + 36 = 0
∴ 6(x – 5x + 6) = 0
∴ x² – 5x + 6 = 0
∴ x² – 2x – 3x + 6=0
∴ x (x – 2) – 3 (x – 2) = 0
∴ x – 3 = 0 अथवा x – 2 = 0
∴ x = 2 अथवा x = 3

अब \(\frac{d^2 y}{d x^2}\) = 12x – 30 x = 2 आगे
\(\frac{d^2 y}{d x^2}\) = 12(2) – 30 = 24 – 30 = -6 < 0 ∴ x = 2 आगे फलन की किंमत महत्तम प्राप्त होगी। x = 3 आगे \(\frac{d^2 y}{d x^2}\) = 12(3) – 30 = 36 – 30 = 6 > 0
∴ x = 3 आगे फलन की न्युनतम किंमत प्राप्त होगी।
y की महत्तम किंमत
x = 2 को फलन y में रखने पर
y = 2x³ – 15x² + 36x + 12 = 2(2)³ – 15(2)² + 36(2) + 12 = 2 × 8 – 15 × 4 + 72 + 12 = 16 – 60 + 84 = 40
y की न्यूनतम किंमत
x = 3 को फलन y में रखने पर
y = 2x³ – 15x² + 36x+ 12
= 2(3)³ – 15(3)² + 36(3) + 12
= 2 × 27 – 15 × 9 + 108 + 12
= 54 – 135 + 120
= 39
x = 2 हो तबy की महत्तम किंमत 40
x = 3 हो तबy की महत्तम किंमत 39

प्रश्न 2.
f(x) = 2x³ + 3x² – 36x + 10 है।x की कौन-सी किंमत के लिए f(x) महत्तम या न्यूनतम होगा?महत्तम और न्यूनतम किंमते ज्ञात कीजिए।
उत्तर :
यहाँ f(x)= 2x³ + 3x² – 36x + 10 ∴ f(x) = 6x² + 6x – 36
स्थिर किंमत के लिए f(x) = 0
∴ 6x² + 6x – 36 = 0
∴ 6(x² – x – 6) = 0
∴ x² + x – 6 = 0
∴ x² + x – 6 = 0
x² + 3x – 2x – 6 = 0
x(x + 3) -2(x + 3) = 0
x – 2 = 0 अथवा x + 3 = 0
∴ x = 2 अथवा x = -3
अब f”(x) = 12x + 6
x = -3 आगे f”(-3)
= -36 + 6
= -30 < 0 = 12 (-3) + 6 ∴ x = -3 आगे फलन की किंमत महत्तम प्राप्त होगी। x = 2 आगे f”(2) = 12(2) + 6 = 24 + 6 = 30 > 0
∴ x = 2 आगे फलन की किंमत न्यूनतम होगी।
f(x) की महत्तम किंमत
x = -3 की फलन f(x) में रखने पर
f(x) = 2x³ + 3x² – 36x + 10
f(-3) = 2(-3)³ + 3(-3)² – 36(-3)+ 10
2x – 27 + 3 × 9 + 108 + 10
= -54 + 27 + 118
= 91

f(x) की न्यूनतम किंमत
x = 2 को फलन f(x) में रखने पर
f(x) = 2x³ + 3x² – 36x + 10
f(2) = 2(2)³ + 3(2)² – 36(2) + 10
= 2 x 8 + 3 × 4 – 72 + 10
= 16 + 12 – 72 + 10 = -34
x = -3 आगे f(x) की महत्तम किंमत = 91
x = 2 आगे f(x) की न्यूनतम किंमत = -34

प्रश्न 3.
f(x) = x³ – x² – x + 2 की महत्तम और न्यूनतम किंमत प्राप्त कीजिए।
उत्तर :
f(x) = x³ – x² – x + 2 ∴ f'(x) = 3x² – 2x – 1
स्थिर किंमत के लिए f'(x) = 0
∴ 3x² – 2x – 1 = 0
3x² – 3x + x – 1 = 0
3x(x – 1) + 1 (x – 1)= 0
3x + 1 = 0 अथवा x – 1 = 0
x = \(\frac{-1}{3}\) अथवा x = 1
अब f”(x) = 6x – 2
x = –\(\frac{1}{3}\) आगे f”(-\(\frac{1}{3}\))= 6 × –\(\frac{1}{3}\) – 2 -4 < 0 ∴ x = –\(\frac{1}{3}\) आगे फलन की किंमत महत्तम प्राप्त होगी। x = 1 आगे f”(1) = 6(1) – 2 = 6 – 2 = 4 > 0
∴ x = 1 आगे फलन की किंमत न्यूनतम होगी।
f(x) की महत्तम किंमत
x = –\(\frac{1}{3}\) को फलन f(x) में रखने पर
f(x) = x³ – x² – x + 2
f(-\(\frac{1}{3}\)) = (-\(\frac{1}{3}\))³ – (-\(\frac{1}{3}\))² – (-\(\frac{1}{3}\)) + 2
= –\(\frac{1}{27}-\frac{1}{9}+\frac{1}{3}\) + 2 = \(\frac{-1-3+9+54}{27}\)
\(\frac{+59}{27}\)

f(x) की न्यूनतम किंमत
x = 1 को f(x) में रखने पर
f(x) = x³ – x² – x + 2
f(1) = (1)³ – (1)² – 1 + 2
= 1 – 1 – 1 + 2 = 1
x = \(-\frac{1}{3}\) आगे f(x) की महत्तम किंमत = \(\frac{59}{27}\)
x = 1 आगे f(x) की न्यूनतम किंमत = 1

प्रश्न 4.
एक उत्पादक 200x + 15x² रू.खर्च करके x इकाई का उत्पादन करता है।मांग का फलन P = 1200 – 10x है,तो लाभ का फलन
ज्ञात कीजिए और महत्तम लाभ के लिए कितनी इकाई का उत्पादन करना चाहिए?
उत्तर :
उत्पादन खर्च का फलन C = 200x + 15x²
माँग का फलन P = 1200 – 10x
आमदानी फलन R = x.P
P = 1200 – 10x रखने पर
R = x (1200 – 10x)
R = 1200x – 10x²
लाभ = आमदानी – खर्च
P = R f” – C
P = 1200x – 10x² – (200x + 15x²)
∴ P = 1200x – 10x² – 200x – 15x²
∴ P = 1000x – 25x²
अब \(\frac{d p}{d x}\) = 1000 – 50x \(\frac{\mathrm{d}^2 \mathrm{p}}{\mathrm{dx}{ }^2}\) = – 50

महत्तम लाभ के लिए
(i) \(\frac{d p}{d x}\) = 0 ∴ 1000 – 50x = 0 ∴ 1000 = 50x ∴ x = \(\frac{1000}{50}\) ∴ x = 20

(ii) \(\frac{\mathrm{d}^2 \mathrm{p}}{\mathrm{dx}{ }^2}\) < 0 \(\frac{\mathrm{d}^2 \mathrm{p}}{\mathrm{dx}{ }^2}\) = -50 < 0
इसलिए x = 20 इकाई का उत्पादन करने से महत्तम लाभ प्राप्त होगा।

प्रश्न 5.
रेफ्रिजरेटर बनानेवाली एक कंपनी अपने रेफ्रिजरेटर का मूल्य ₹ 10,000 रखती है। x रेफिजरेटर बनाने का कुल खर्च
C = 0.1x² + 9000x + 100 ₹ है। कितने रेफ्रिजरेटर बनाने से लाभ महत्तम होगा?
उत्तर :
कुल खर्च का फलन C = 0.1x² + 9000x + 100
x रेफ्रिजरेटर की बिक्री से आमदानी R= 10000x
P = R – C
= 10000x – (0.1x² + 9000x + 100)
= 10000x – 0.1x² – 9000x – 100
∴ P = 1000x – 0.1x² – 100
∴ \(\frac{d p}{d x}\) = 1000 – 0.2x और \(\frac{d p}{d x}\) = -0.2

महत्तम लाभ के लिए:
(i) \(\frac{d p}{d x}\) = 0 ∴ 1000 – 0.2x = 0 0.2x = 1000 ∴ x = \(\frac{1000}{0.2}\) ∴ x = 5000

(ii) \(\frac{\mathrm{d}^2 \mathrm{p}}{\mathrm{dx}{ }^2}\) = -0.2 < 0
इसलिए 5000 रेफ्रिजरेटर बनाने से महत्तम लाभ होगा।

प्रश्न 6.
एक खिलौना ₹ 20 में बेचा जाता है। ऐसे x खिलौने को बनाने का कुल खर्च C = 1000 + 16.5x + 0.001x ₹ होता है। कितने खिलौने बनाने से लाभ महत्तम होगा?
उत्तरः
एक खिलौने का मूल्य = 20 ₹
कुल खर्च C = 1000 + 16.5x + 0.001x²
x खिलौने की बिक्री से आमदानी R= 20x
लाभ का फलन P = R – C
= 20x – (1000 + 16.5x + 0.001x²)
= 20x – 1000 – 16.5x – 0.001x²
P = 3.5x – 1000 – 0.001x²
∴ \(\frac{d p}{d x}\) = 3.5 – 0 – 0.002x = 3.5 – 0.002x और \(\frac{\mathrm{d}^2 \mathrm{p}}{\mathrm{dx}{ }^2}\) = -0.002

महत्तम लाभ के लिए :
(i) \(\frac{d p}{d x}\) = 0 ∴ 3.5 – 0.002x = 0 ∴ x = \(\frac{3.5}{0.002}\) ∴ x = 1750

(ii) \(\frac{\mathrm{d}^2 \mathrm{p}}{\mathrm{dx}{ }^2}\) < 0 \(\frac{\mathrm{d}^2 \mathrm{p}}{\mathrm{dx}{ }^2}\) = -0.002 < 0
इसलिए 1750 खिलौने बनाने से लाभ महत्तम होगा।