Gujarat Board GSEB Solutions Class 6 Maths Chapter 3 સંખ્યા સાથે Ex 3.3 Textbook Exercise Questions and Answers.
Gujarat Board Textbook Solutions Class 6 Maths Chapter 3 સંખ્યા સાથે Ex 3.3
પ્રશ્ન 1.
વિભાજ્યતાની ચાવીનો ઉપયોગ કરીને નીચેની કઈ સંખ્યા 2 વડે, 3 વડે, 4 વડે, 5 વડે, 6 વડે, 8 વડે, 9 વડે, 10 વડે અને 11 વડે વિભાજ્ય છે તે નક્કી કરોઃ
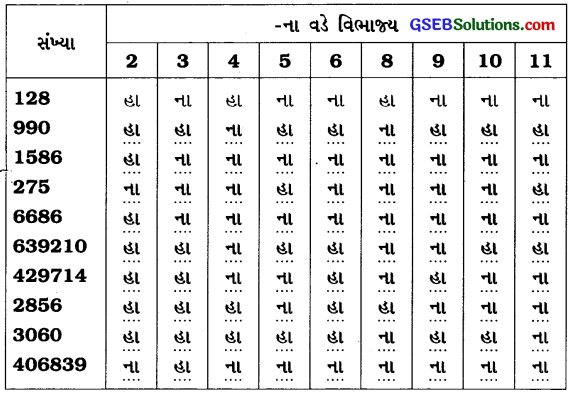
જવાબ:
સમજૂતીઃ [યાદ રાખો …..]
2 માટે સંખ્યાનો એકમનો અંક 0, 2, 4, 6 કે 8 હોય તેને 2 વડે નિઃશેષ ભાગી શકાય.
૩ માટેઃ સંખ્યાના અંકોના સરવાળાને 3 વડે નિઃશેષ ભાગી શકાય, તો સંખ્યાને 3 વડે નિઃશેષ ભાગી શકાય.
4 માટે સંખ્યાના એકમ અને દશકના બે અંકોથી બનતી સંખ્યાને 4 વડે નિઃશેષ ભાગી શકાય, તો સંખ્યાને 4 વડે નિઃશેષ ભાગી શકાય.
5 માટે સંખ્યાનો એકમનો અંક અથવા 5 હોય, તો સંખ્યાને 5 વડે નિઃશેષ ભાગી શકાય.
6 માટે સંખ્યાને 2 વડે અને 3 વડે નિઃશેષ ભાગી શકાય, તો સંખ્યાને 6 વડે નિઃશેષ ભાગી શકાય.
8 માટે સંખ્યાના છેલ્લા ત્રણ અંકો (સો, દશક અને એકમ) વડે બનતી સંખ્યાને 8 વડે ભાગી શકાય, તો સંખ્યાને 8 વડે નિઃશેષ ભાગી શકાય.
9 માટે સંખ્યાના અંકોના સરવાળાને 9 વડે નિઃશેષ ભાગી શકાય, તો સંખ્યાને 9 વડે નિઃશેષ ભાગી શકાય.
10 માટે જો સંખ્યાનો એકમનો અંક હોય, તો સંખ્યાને 10 વડે નિઃશેષ ભાગી શકાય.
11 માટે જો સંખ્યાના જમણી બાજુથી એકી સ્થાનના અંકો અને જમણી બાજુથી બેકી સ્થાનના અંકોનો તફાવત છે હોય અથવા 11નો ગુણક હોય, તો તે સંખ્યાને 11 વડે નિઃશેષ ભાગી શકાય.
![]()
પ્રશ્ન 2.
વિભાજ્યતાની ચાવીનો ઉપયોગ કરીને નીચેનામાંથી કઈ સંખ્યા 4 અને 8 વડે વિભાજ્ય છે તે નક્કી કરોઃ
(a) 572
(b) 726352
(c) 5500
(d) 6000
(e) 12159
(f) 14560
(g) 21084
(h) 31795072
(i) 1700
(j) 2150
જવાબ :
સમજૂતીઃ
(i) જે સંખ્યાના છેલ્લા બે અંકો વડે બનતી સંખ્યાને 4 વડે નિઃશેષ ભાગી શકાય, તો તે સંખ્યાને 4 વડે નિઃશેષ ભાગી શકાય.
(ii) જે સંખ્યાના છેલ્લા ત્રણ અંકો વડે બનતી સંખ્યાને 8 વડે નિઃશેષ ભાગી શકાય, તો તે સંખ્યાને 8 વડે નિઃશેષ ભાગી શકાય.
(a) 572.
(i) છેલ્લા બે અંકો વડે બનતી સંખ્યા 72 છે. 72 ÷ 4 = 18
∴ 572ને 4 વડે નિઃશેષ ભાગી શકાય.
(ii) છેલ્લા ત્રણ અંકો વડે બનતી સંખ્યા 572 છે.
(∵ 572 ÷ 8 = 71\(\frac{4}{8}\))
∴ 572ને 8 વડે નિઃશેષ ભાગી ન શકાય.
(b) 726352
(i) છેલ્લા બે અંકો વડે બનતી સંખ્યા 52 છે. 52 ÷ 4 = 13
∴ 726352ને 4 વડે નિઃશેષ ભાગી શકાય.
(ii) છેલ્લા ત્રણ અંકો વડે બનતી સંખ્યા 352 છે. 352 ÷ 8 = 44
∴ 726352ને 8 વડે નિઃશેષ ભાગી શકાય.
[નોંધ: ઉપર મુજબ હવે નીચેના દાખલા ગણી શકાય.]
(c) 5500
5500ને 4 વડે નિઃશેષ ભાગી શકાય.
5500ને 8 વડે નિઃશેષ ભાગી ન શકાય.
(d) 6000
6000ને 4 વડે નિઃશેષ ભાગી શકાય.
6000ને 8 વડે નિઃશેષ ભાગી શકાય.
(e) 12159
12159ને 4 વડે નિઃશેષ ભાગી ન શકાય.
12159ને 8 વડે નિઃશેષ ભાગી ન શકાય.
(f) 14560
14560ને 4 વડે નિઃશેષ ભાગી શકાય.
14560ને 8 વડે નિઃશેષ ભાગી શકાય.
(g) 21084
21084ને 4 વડે નિઃશેષ ભાગી શકાય.
21084ને 8 વડે નિઃશેષ ભાગી ન શકાય.
(h) 31795072
31795072ને 4 વડે નિઃશેષ ભાગી શકાય.
31795072ને 8 વડે નિઃશેષ ભાગી શકાય.
(i) 1700
1700ને 4 વડે નિઃશેષ ભાગી શકાય.
1700ને 8 વડે નિઃશેષ ભાગી ન શકાય.
(j) 2150
2150ને 4 વડે નિઃશેષ ભાગી ન શકાય.
2150ને 8 વડે નિઃશેષ ભાગી ન શકાય.
![]()
પ્રશ્ન ૩.
વિભાજ્યતાની ચાવીનો ઉપયોગ કરીને નીચેનામાંથી કઈ સંખ્યા 6 વડે વિભાજ્ય છે તે નક્કી કરોઃ
(a) 297144
(b) 1258
(c) 4335
(d) 61233
(e) 901352
(f) 438750
(g) 1790184
(h) 12583
(i) 639210
(j) 17852
જવાબ:
સમજૂતીઃ જો સંખ્યાને 2 અને 3 બંને વડે નિઃશેષ ભાગી શકાય, તો જ સંખ્યાને 6 વડે નિઃશેષ ભાગી શકાય.
2 વડે નિઃશેષ ભાગવા માટે સંખ્યાનો છેલ્લો અંક 0, 2, 4, 6 કે 8 હોવો જોઈએ.
3 વડે નિઃશેષ ભાગવા માટે સંખ્યાના અંકોના સરવાળાને 3 વડે નિઃશેષ ભાગવા જોઈએ.
(a) 297144
(i) સંખ્યાનો એકમનો અંક 4 છે. તેથી સંખ્યાને 2 વડે નિઃશેષ ભાગી શકાય.
(ii) સંખ્યાના અંકોનો સરવાળો = 2 + 9 + 7 + 1 + 4 + 4 = 27
27ને 3 વડે નિઃશેષ ભાગી શકાય છે.
આમ, સંખ્યાને 2 અને 3 બંને વડે નિઃશેષ ભાગી શકાય છે.
∴ 297144ને 6 વડે નિઃશેષ ભાગી શકાય.
(b) 1258
(i) સંખ્યાનો એકમનો અંક 8 છે. તેથી સંખ્યાને 2 વડે નિઃશેષ ભાગી શકાય.
(ii) સંખ્યાના અંકોનો સરવાળો = 1 + 2 + 5 + 8 = 16
16ને 3 વડે નિઃશેષ ભાગી ન શકાય. આમ, સંખ્યાને 2 વડે નિઃશેષ ભાગી શકાય છે પણ 3 વડે નિઃશેષ ભાગી શકાતી નથી.
∴ 1258ને 6 વડે નિઃશેષ ભાગી ન શકાય.
(c) 4335
સંખ્યાનો એકમનો અંક 5 છે. તેથી સંખ્યાને 2 વડે નિઃશેષ ભાગી ન શકાય. તેથી સંખ્યાને 3 વડે નિઃશેષ ભાગી શકાય છે કે કેમ તે ચકાસવાની જરૂર નથી.
∴ 4335ને 6 વડે નિઃશેષ ભાગી ન શકાય.
(d) 61233
સંખ્યાનો એકમનો અંક 3 છે. તેથી સંખ્યાને 2 વડે નિઃશેષ ભાગી ન શકાય.
∴ 61233ને 6 વડે નિઃશેષ ભાગી ન શકાય.
(e) 901352
(i) સંખ્યાનો એકમનો અંક 2 છે. તેથી સંખ્યાને 2 વડે નિઃશેષ ભાગી શકાય.
(ii) સંખ્યાના અંકોનો સરવાળો = 2 + 5 + 3 + 1 + 9 = 20
20ને 3 વડે નિઃશેષ ભાગી ન શકાય.
∴ 901352ને 6 વડે નિઃશેષ ભાગી ન શકાય.
(f) 438750
(i) 438750નો એકમનો અંક 0 છે. તેથી સંખ્યાને 2 વડે નિઃશેષ ભાગી શકાય.
(ii) સંખ્યાના અંકોનો સરવાળો = 0 + 5 + 7 + 8 + 1 + 4 = 27
27ને 3 વડે નિઃશેષ ભાગી શકાય.
∴ 438750ને 6 વડે નિઃશેષ ભાગી શકાય.
(g) 1790184
179 184ને 6 વડે નિઃશેષ ભાગી શકાય. (ઉપર મુજબ ચકાસો.)
(h) 12583
12583ને 6 વડે નિઃશેષ ભાગી ન શકાય.
જુઓ : 12583 એ એકી સંખ્યા છે.
(i) 639210
639210ને 6 વડે નિઃશેષ ભાગી શકાય. (ઉપર મુજબ ચકાસો.)
(j) 17852
17852ને 6 વડે નિઃશેષ ભાગી ન શકાય. (ઉપર મુજબ ચકાસો.)
પ્રશ્ન 4.
વિભાજ્યતાની ચાવીનો ઉપયોગ કરીને નીચેનામાંથી કઈ સંખ્યા 11 વડે વિભાજ્ય છે તે નક્કી કરોઃ
(a) 5445
(b) 10824
(c) 738965
(d) 70169308
(e) 10000001
(f) 901153
જવાબ:
સમજૂતી સંખ્યાના જમણી બાજુથી એકી સ્થાનમાંના અંકોનો સરવાળો અને સંખ્યાના જમણી બાજુથી બેકી સ્થાનમાંના અંકોનો સરવાળાનો તફાવત શૂન્ય હોય. અથવા 11નો ગુણક હોય, તો સંખ્યાને 11 વડે નિઃશેષ ભાગી શકાય.
(a) 5445
સંખ્યાની જમણી બાજુથી એકી સ્થાનના અંકોનો સરવાળો = 5 + 4 = 9
સંખ્યાની જમણી બાજુથી બેકી સ્થાનના અંકોનો સરવાળો = 4 + 5 = 9
આ બંને સરવાળાનો તફાવત = 9 – 9 = 0
આ સરવાળો 0 છે.
∴ 5445ને 11 વડે નિઃશેષ ભાગી શકાય.
(b) 10824
સંખ્યાની જમણી બાજુથી એકી સ્થાનના અંકોનો સરવાળો = 4 + 8 + 1 = 13
સંખ્યાની જમણી બાજુથી બેકી સ્થાનના અંકોનો સરવાળો = 2 + 0 = 2
આ બંને સરવાળાનો તફાવત = 13 – 2 = 11
આ તફાવત 11નો ગુણક (11 × 1 = 11) છે.
∴ 10824ને 11 વડે નિઃશેષ ભાગી શકાય.
(c) 7138965
સંખ્યાની જમણી બાજુથી એકી સ્થાનના અંકોનો સરવાળો = 5 + 9 + 3 + 7 = 24
સંખ્યાની જમણી બાજુથી બેકી સ્થાનના અંકોનો સરવાળો = 6 + 8 + 1 = 15
આ બંને સરવાળાનો તફાવત = 24 – 15 = 9 અહીં તફાવત છે નથી કે 11નો ગુણક પણ નથી.
∴ 7138965ને 11 વડે નિઃશેષ ભાગી ન શકાય.
(d) 70169308
સંખ્યાની જમણી બાજુથી એકી સ્થાનના અંકોનો સરવાળો = 8 + 3 + 6 + 0 = 17
સંખ્યાની જમણી બાજુથી બેકી સ્થાનના અંકોનો સરવાળો = 0 + 9 + 1 + 7 = 17
આ બંને સરવાળાનો તફાવત = 17 – 17 = 0
અહીં તફાવત છે છે.
∴ 70169308ને 11 વડે નિઃશેષ ભાગી શકાય.
(e) 10000001
સંખ્યાની જમણી બાજુથી એકી સ્થાનના અંકોનો સરવાળો = 1 + 0 + 0 + 0 = 1
સંખ્યાની જમણી બાજુથી બેકી સ્થાનના અંકોનો સરવાળો = 0 + 0 + 0 + 1 = 1
આ બંને સરવાળાનો તફાવત = 1 – 1 = 0
અહીં તફાવત 0 છે.
∴ 10000001ને 11 વડે નિઃશેષ ભાગી શકાય છે.
(f) 901153
સંખ્યાની જમણી બાજુથી એકી સ્થાનના અંકોનો સરવાળો = 3 + 1 + 0 = 4
સંખ્યાની જમણી બાજુથી બેકી સ્થાનના અંકોનો સરવાળો = 5 + 1 + 9 = 15
આ બંને સરવાળાનો તફાવત = 15 – 4 = 11
અહીં તફાવત 11નો ગુણક છે. (11 × 1 = 11)
∴ 901153ને 11 વડે નિઃશેષ ભાગી શકાય છે.
![]()
પ્રશ્ન 5.
નીચે આપેલી સંખ્યાની દરેક ખાલી જગ્યામાં સૌથી નાનો અને સૌથી મોટો અંક લખો. જેથી તે સંખ્યાને ૩ વડે ભાગી શકાય?
(a) …..6724
(b) 4765……2
જવાબ :
સમજૂતીઃ આ માટે આપેલી અધૂરી સંખ્યાના અંકોનો સરવાળો કરીશું. આ સરવાળાને 3ના ગુણક જે આ સરવાળાથી વધારે હોય તેની સાથે બાદબાકી કરીશું.
(a) …..6724
આપેલ અંકોનો સરવાળો = 6 + 7 + 2 + 4 = 19.
હવે, 19 કરતાં વધુ હોય તેવા 3ના ગુણક 21, 24, 27, 30, … છે.
∴ 21 – 19 = 2, 24 – 19 = 5, 27 – 19 = 8, 30 – 19 = 11, …
11 એ બે અંકનો છે. તે અવગણીશું.
∴ સૌથી નાનો અંક 2 અને સૌથી મોટો અંક 8 હોઈ શકે.
(b) 4765..2
આપેલ અંકોનો સરવાળો = 4 + 7 + 6 + 5 + 2 = 24
24 એ 3નો ગુણક જ છે. તેથી સૌથી નાનો અંક ) હોઈ શકે.
હવે, 24થી મોટા 3ના ગુણક 27, 30, 33, 36, … છે.
∴ 27 – 24 = 3, 30 – 24 = 6, 33 – 24 = 9, 36 – 24 = 12,……
12 એ બે અંકનો છે. તે અવગણીશું.
∴ સૌથી મોટો અંક 9 હોઈ શકે.
આમ, સૌથી નાનો અંક છે અને સૌથી મોટો અંક 9 હોઈ શકે.
પ્રશ્ન 6.
નીચે આપેલી સંખ્યાની દરેક ખાલી જગ્યામાં સૌથી નાનો અને સૌથી મોટો અંક લખો. જેથી તે સંખ્યાને 11 વડે ભાગી શકાય?
(a) 92…389
(b) 8…9484
જવાબ:
સમજૂતી સંખ્યાના જમણી બાજુથી એકી સ્થાનના અંકોનો સરવાળો અને સંખ્યાના જમણી બાજુથી બેકી સ્થાનના અંકોનો સરવાળાનો તફાવત છે અથવા 11નો ગુણક હોય, તો સંખ્યાને 11 વડે ભાગી શકાય.
(a) 92…..389
ખૂટતા અંકને x કહીએ.
તો સંખ્યા 92×389 છે.
સંખ્યાના જમણી બાજુથી એકી સ્થાનના અંકોનો સરવાળો = 9 + 3 + 2 = 14
સંખ્યાના જમણી બાજુથી બેકી સ્થાનના અંકોનો સરવાળો = 8 + x + 9 = 17 + x
(i) સંખ્યાને 11 વડે ભગાવા માટે આ બંને સરવાળાનો તફાવત 0 થવો જોઈએ.
∴ (17 + x) – 14 = 0
∴ 17 + x – 14 = 0
∴ x + 3 = 0
∴ x = -3
જે ત્રણ સંખ્યા છે એટલે અશક્ય છે.
(ii) સંખ્યાને 11 વડે ભગાવા માટે બંને સરવાળાનો તફાવત 11નો ગુણક થવો જોઈએ.
11ના ગુણક 11, 22, 33, … છે.
તફાવત x + 3 = 11 લેતાં x = 8 મળે, x + 3 = 22 લેતાં
x = 19 મળે જે બે અંકોની છે.
∴ x = 8
આમ, સંખ્યા 928389
(b) 8…..9484
ખૂટતા અંકને x કહીએ.
તો સંખ્યા 8×9484 થાય.
સંખ્યાના જમણી બાજુથી એકી સ્થાનના અંકોનો સરવાળો = 4 + 4 + x = 8 + x
સંખ્યાના જમણી બાજુથી બેકી સ્થાનના અંકોનો સરવાળો = 8 + 9 + 8 = 25
(i) સંખ્યાને 11 વડે ભગાવા માટે આ બંને સરવાળાનો તફાવત 0 થવો જોઈએ.
∴ 25 – (8 + x) = 0.
∴ 25 – 8 – x = 0 ∴ 17 – x = 0 ∴ x = 17
17 બે અંકની સંખ્યા છે એટલે અશક્ય છે.
(ii) સંખ્યાને 11 વડે ભગાવા માટે બંને સરવાળાનો તફાવત 11નો ગુણક થવો જોઈએ.
11ના ગુણક 11, 22, 33, … છે.
તફાવત 11 લેતાં 17 – x = 11 . ∴ x = 17 – 11 ∴ x = 6
આમ, સંખ્યા 869484