GSEB Solutions Class 7 Maths Chapter 11 પરિમિતિ અને ક્ષેત્રફળ Ex 11.2

Gujarat Board GSEB Solutions Class 7 Maths Chapter 11 પરિમિતિ અને ક્ષેત્રફળ Ex 11.2 Textbook Exercise Questions and Answers.

Gujarat Board Textbook Solutions Class 7 Maths Chapter 11 પરિમિતિ અને ક્ષેત્રફળ Ex 11.2

1. નીચેના દરેક સમાંતરબાજુ ચતુષ્કોણોનાં ક્ષેત્રફળ શોધો:

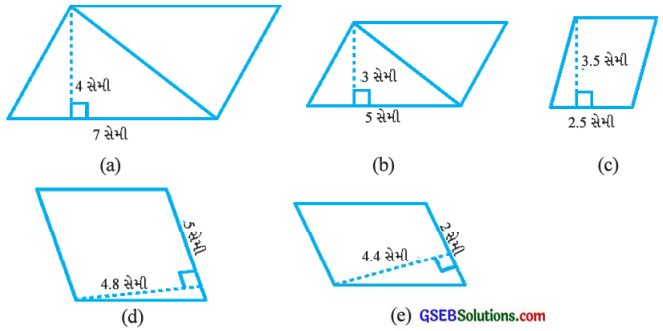
જવાબ:
(a) અહીં સમાંતરબાજુ ચતુષ્કોણનો પાયો b = 7 સેમી, ઊંચાઈ h = 4 સેમી
∴ સમાંતરબાજુ ચતુષ્કોણનું ક્ષેત્રફળ = b × h
= 7 સેમી × 4 સેમી = 28 સેમી²
(b) અહીં સમાંતરબાજુ ચતુષ્કોણનો પાયો b = 5 સેમી, ઊંચાઈ h = 3 સેમી
∴ સમાંતરબાજુ ચતુષ્કોણનું ક્ષેત્રફળ = b × h
= 5 સેમી × 3 સેમી = 15 સેમી²
(c) અહીં સમાંતરબાજુ ચતુષ્કોણનો પાયો b = 2.5 સેમી, ઊંચાઈ h = 3.5 સેમી
∴ સમાંતરબાજુ ચતુષ્કોણનું ક્ષેત્રફળ = b × h
= 2.5 સેમી × 3.5 સેમી
= 8.75 સેમી²
(d) અહીં સમાંતરબાજુ ચતુષ્કોણનો પાયો b = 5 સેમી, ઊંચાઈ h = 4.8 સેમી
∴ સમાંતરબાજુ ચતુષ્કોણનું ક્ષેત્રફળ = b × h
= 5 સેમી × 4.8 સેમી
= 24 સેમી²
(e) અહીં સમાંતરબાજુ ચતુષ્કોણનો પાયો b = 2 સેમી, ઊંચાઈ h = 4.4 સેમી
∴ સમાંતરબાજુ ચતુષ્કોણનું ક્ષેત્રફળ = b × h = 2 સેમી × 4.4 સેમી
= 8.8 સેમી²

પ્રશ્ન 2.
નીચેના દરેક ત્રિકોણનાં ક્ષેત્રફળ શોધો:

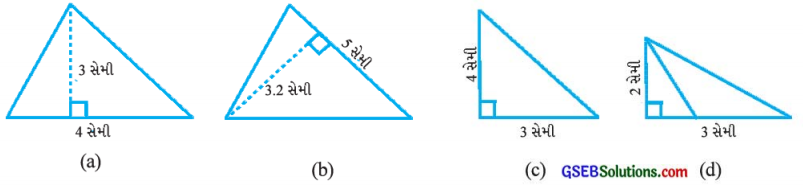
જવાબ:
(a) અહીં ત્રિકોણનો પાયો b = 4 સેમી, ઊંચાઈ h = 3 સેમી
∴ ત્રિકોણનું ક્ષેત્રફળ = \(\frac {1}{2}\) × b × h
= \(\frac {1}{2}\) × 4 × 3 સેમી² = 6 સેમી²

(b) અહીં ત્રિકોણનો પાયો b = 5 સેમી, ઊંચાઈ h = 3.2 સેમી
∴ ત્રિકોણનું ક્ષેત્રફળ = \(\frac {1}{2}\) × b × h
= \(\frac {1}{2}\) × 5 × 3.2 સેમી² = 8 સેમી²

(c) અહીં ત્રિકોણનો પાયો b = 3 સેમી, ઊંચાઈ h = 4 સેમી
∴ ત્રિકોણનું ક્ષેત્રફળ = \(\frac {1}{2}\) × b × h
= \(\frac {1}{2}\) × 3 × 4 સેમી² = 6 સેમી²

(d) અહીં ત્રિકોણનો પાયો b = 3 સેમી, ઊંચાઈ h = 2 સેમી
∴ ત્રિકોણનું ક્ષેત્રફળ = \(\frac {1}{2}\) × b × h
= \(\frac {1}{2}\) × 3 × 2 સેમી² = 3 સેમી²

પ્રશ્ન 3.
ખૂટતાં મૂલ્યો શોધો:

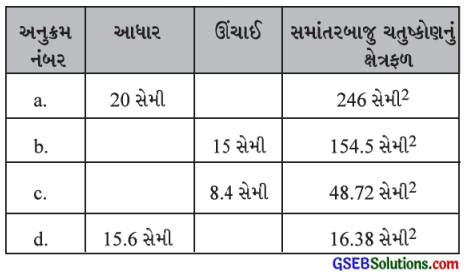
જવાબ:
(a) અહીં સમાંતરબાજુ ચતુષ્કોણનું ક્ષેત્રફળ = 246 સેમી² અને આધાર b = 20 સેમી
∴ સમાંતરબાજુ ચતુષ્કોણનું ક્ષેત્રફળ = b × h
∴ 246 = 20 × h
∴ h = \(\frac {246}{20}\)
∴ h = 12.3 સેમી
∴ ખૂટતી માહિતી ઊંચાઈ = 12.8 સેમી

(b) અહીં સમાંતરબાજુ ચતુષ્કોણનું ક્ષેત્રફળ = 154.5 સેમી² અને ઊંચાઈ h = 15 સેમી
∴ સમાંતરબાજુ ચતુષ્કોણનું ક્ષેત્રફળ = b × h
∴ 154.5 = b × 15
∴ b = \(\frac {154.5}{15}\)
∴ b = 10.3 સેમી
∴ ખૂટતી માહિતી આધાર = 10.3 સેમી

(c) અહીં સમાંતરબાજુ ચતુષ્કોણનું ક્ષેત્રફળ = 48.72 સેમી² અને ઊંચાઈ h = 8.4 સેમી
∴ સમાંતરબાજુ ચતુષ્કોણનું ક્ષેત્રફળ = b × h
∴ 48.72 = b × 8.4
∴ b = \(\frac {48.72}{8.4}\)
∴ b = 5.8 સેમી
∴ ખૂટતી માહિતી આધાર = 5.8 સેમી

(d) અહીં સમાંતરબાજુ ચતુષ્કોણનું ક્ષેત્રફળ = 16.38 સેમી² અને આધાર b = 15.6 સેમી
∴ સમાંતરબાજુ ચતુષ્કોણનું ક્ષેત્રફળ = b × h
∴ 16.38 = 15.6 × h
∴ h = \(\frac {16.38}{15.6}\)
∴ h = 1.05 સેમી
∴ ખૂટતી માહિતી ઊંચાઈ = 1.05 સેમી

પ્રશ્ન 4.
ખૂટતાં મૂલ્યો શોધોઃ

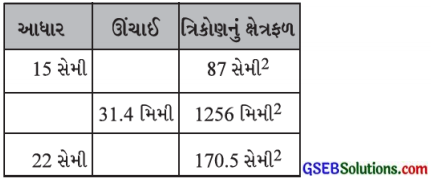
જવાબ:
(i) અહીં ત્રિકોણનું ક્ષેત્રફળ = 87 સેમી² અને આધાર b = 15 સેમી
ત્રિકોણનું ક્ષેત્રફળ = \(\frac {1}{2}\) × b × h
∴ 87 = \(\frac {1}{2}\) × 15 × h
∴ h = \(\frac{87 \times 2}{15}\)
∴ h = \(\frac {174}{15}\) = 11.6 સેમી
∴ ખૂટતી માહિતી ઊંચાઈ = 11.6 સેમી

(ii) અહીં ત્રિકોણનું ક્ષેત્રફળ = 1256 મિમી² અને ઊંચાઈ h = 31.4 મિમી
ત્રિકોણનું ક્ષેત્રફળ = \(\frac {1}{2}\) × b × h
∴ 1256 = \(\frac {1}{2}\) × b × 31.4
∴ b = \(\frac{1256 \times 2}{31.4}\)
∴ b = \(\frac {2512}{31.4}\)
∴ b = 80 મિમી
∴ ખૂટતી માહિતી આધાર = 80 મિમી

(iii) અહીં ત્રિકોણનું ક્ષેત્રફળ = 170.5 સેમી², આધાર b = 22 સેમી
ત્રિકોણનું ક્ષેત્રફળ = \(\frac {1}{2}\) × b × h
∴ 170.5 = \(\frac {1}{2}\) × 22 × h
∴ h = \(\frac{170.5 \times 2}{22}\)
∴ h = \(\frac {170.5}{11}\)
∴ h = 15.5 સેમી
∴ ખૂટતી માહિતી ઊંચાઈ = 15.5 સેમી

પ્રશ્ન 5.
PQRS સમાંતરબાજુ ચતુષ્કોણ છે. Qમાંથી SR પરની ઊંચાઈ QM છે અને Qમાંથી PS પરની ઊંચાઈ QN છે. જો SR = 12 સેમી અને QM = 7.6 સેમી હોય, તો (a) સમાંતરબાજુ ચતુષ્કોણ PQRSનું ક્ષેત્રફળ (b) જો PS = 8 સેમી હોય, તો QN શોધો.

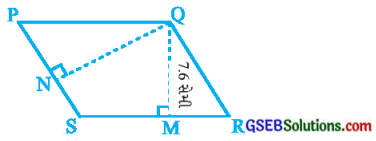
જવાબ:
(a) અહીં સમાંતરબાજુ ચતુષ્કોણ PQRSમાં પાયા SRને અનુરૂપ વેધ QM છે.
b = SR = 12 સેમી અને h = QM = 7.6 સેમી
સમાંતરબાજુ ☐PQRSનું ક્ષેત્રફળ = b × h
= SR × QM
= 12 × 7.6 = 91.2 સેમી²

(b) સમાંતરબાજુ ચતુષ્કોણ PQRSનું ક્ષેત્રફળ 91.2 સેમી², પાયો b = PS = 8 સેમી અને ઊંચાઈ h = QN = ?
સમાંતરબાજુ ☐PQRSનું ક્ષેત્રફળ = b × h
∴ 91.2 = 8 × h
∴ h = \(\frac {91.2}{8}\)
∴ h = 11.4 સેમી
∴ QN = 11.4 સેમી

પ્રશ્ન 6.
સમાંતરબાજુ ચતુષ્કોણ ABCDમાં DL અને BM અનુક્રમે બાજુઓ AB અને AD પરની ઊંચાઈઓ છે. જો સમાંતરબાજુ ચતુષ્કોણનું ક્ષેત્રફળ 1470 સેમી² હોય અને AB = 35 સેમી તથા AD = 49 સેમી હોય, તો BM અને DLની લંબાઈ શોધો.

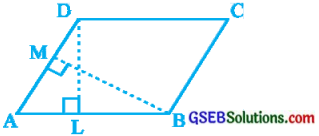
જવાબઃ
સમાંતરબાજુ ચતુષ્કોણ ABCDનું ક્ષેત્રફળ = 1470 સેમી², પાયો b = AD = 49 સેમી અને અનુરૂપ વેધ h = BM = ?
☐ABCDનું ક્ષેત્રફળ = AD × BM
∴ 1470 = 49 × BM
∴ BM = \(\frac {1470}{49}\)
∴ BM = 30 સેમી
હવે, સમાંતરબાજુ ચતુષ્કોણ ABCDનું ક્ષેત્રફળ = 1470 સેમી², પાયો b = AB = 15 સેમી અને અનુરૂપ વેધ h = DL = ? ☐ABCDનું ક્ષેત્રફળ = AB × DL
∴ 1470 = 35 × DL
∴ DL = \(\frac {1470}{35}\)
∴ DL = 42 સેમી
આમ, BM = 30 સેમી અને DL = 42 સેમી

પ્રશ્ન 7.
∆ABCમાં \(\angle\)A કાટખૂણો છે. \(\overline{\mathbf{A D}}\) એ \overline{\mathbf{B C}}ને . લંબ છે. જો AB = 5 સેમી, BC = 13 સેમી અને AC = 12 સેમી હોય, તો ∆ABCનું ક્ષેત્રફળ શોધો. ADની લંબાઈ પણ શોધો.

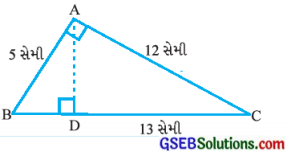
જવાબઃ
કાટકોણ ∆ABCમાં પાયો \(\overline{\mathbf{A B}}\) છે અને વેધ \(\overline{\mathbf{A C}}\) છે. (∵ \(\angle\)A કાટખૂણો છે)
AB = 5 સેમી અને AC = 12 સેમી છે.
∆ABCનું ક્ષેત્રફળ = \(\frac {1}{2}\) × પાયો × વેધ
= \(\frac {1}{2}\) × 5 × 12 = 30 સેમી²
હવે, આ ∆ABCમાં \(\overline{\mathbf{B C}}\) પાયા ઉપર વેધ \(\overline{\mathbf{A D}}\) છે. BC = 13 સેમી છે.
∆ABCનું ક્ષેત્રફળ = 30 સેમી²
∆ABCનું ક્ષેત્રફળ = \(\frac {1}{2}\) × પાયો × વેધ
30 = \(\frac {1}{2}\) × 13 × AD
∴ AD = \(\frac{30 \times 2}{13}\)
∴ AD = 3 સેમી
આમ, ∆ABCનું ક્ષેત્રફળ 30 સેમી² અને AD = \(\frac {60}{13}\) સેમી

પ્રશ્ન 8.
∆ABC સમઢિબાજુ ત્રિકોણ છે. જેમાં AB = AC = 7.5 સેમી અને BC = 9 સેમી છે. Aમાંથી BC પરની ઊંચાઈ AD = 6 સેમી છે. ∆ABCનું ક્ષેત્રફળ શોધો. C માંથી \(\overline{\mathbf{A B}}\) પરની ઊંચાઈ એટલે કે CE કેટલી થશે?

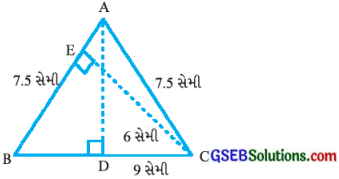
જવાબઃ
∆ABCના પાયા BC ઉપર વેધ AD છે. BC = 9 સેમી અને AD = 6 સેમી છે.
∆ABCનું ક્ષેત્રફળ = \(\frac {1}{2}\) × BC × AD
= \(\frac {1}{2}\) × 9 × 6 = 9 x 3 = 27 સેમી²
હવે, ∆ABCના પાયા \(\overline{\mathbf{A B}}\) ઉપર વેધ \(\overline{\mathbf{C E}}\) છે. AB = 7.5 સેમી અને ત્રિકોણનું ક્ષેત્રફળ 27 સેમી² છે.
∆ABCનું ક્ષેત્રફળ = \(\frac {1}{2}\) × AB × CE
27 = \(\frac {1}{2}\) × 7.5 x CE
∴ CE = \(\frac{27 \times 2}{7.5}\)
∴ CE = \(\frac {54}{7.5}\)
∴ CE = 7.2 સેમી
આમ, ∆ABCનું ક્ષેત્રફળ 27 સેમી² અને CE = 7.2 સેમી