Gujarat Board GSEB Solutions Class 7 Maths Chapter 11 પરિમિતિ અને ક્ષેત્રફળ Ex 11.4 Textbook Exercise Questions and Answers.
Gujarat Board Textbook Solutions Class 7 Maths Chapter 11 પરિમિતિ અને ક્ષેત્રફળ Ex 11.4
પ્રશ્ન 1.
એક બાગ 90 મી લાંબો અને 75 મી પહોળો છે. તેની ફરતે ચારે તરફ બહારની બાજુએ 5 મી પહોળો રસ્તો બનાવવાનો છે. આ રસ્તાનું ક્ષેત્રફળ શોધો. બાગનું ક્ષેત્રફળ કેટલા હેક્ટર છે?
જવાબઃ
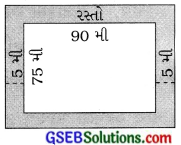
90 મી
લંબચોરસ બાગની લંબાઈ (l) = 90 મી
લંબચોરસ બાગની પહોળાઈ (b) = 75 મી
∴ લંબચોરસ બાગનું ક્ષેત્રફળ = l × b
= 90 મી × 75 મી = 6750 મી2
હવે, 1 મી2 = \(\frac {1}{10,000}\) હેક્ટર
∴ 6750 મી2 = \(\frac {6750}{10,000}\) હેક્ટર = 0.675 હેક્ટર
આ બાગની બહારની ચારે બાજુએ ફરતો 5 મી પહોળાઈનો રસ્તો છે.
∴ રસ્તા સાથે લંબચોરસ બાગની લંબાઈ = (90 + 5 + 5) મી = 100 મી
અને રસ્તા સાથે લંબચોરસ બાગની પહોળાઈ = (75 + 5 + 5) મી = 85 મી
રસ્તા સાથેના મોટા લંબચોરસનું ક્ષેત્રફળ = લંબાઈ × પહોળાઈ
= 100 મી × 85 મી = 8500 મી2
∴ રસ્તાનું ક્ષેત્રફળ = મોટા લંબચોરસનું ક્ષેત્રફળ – બાગનું ક્ષેત્રફળ
= 8500 મી2 – 6750 મી2 = 1750 મી2
આમ, બાગનું ક્ષેત્રફળ 0.675 હેક્ટર અને રસ્તાનું ક્ષેત્રફળ 1750 મી2
![]()
પ્રશ્ન 2.
125 મી લંબાઈ અને 65 મી પહોળાઈ ધરાવતા એક લંબચોરસ બાગની ફરતે ચારે તરફ બહારની બાજુએ ૩ મીટર પહોળો રસ્તો છે. આ રસ્તાનું ક્ષેત્રફળ શોધો.
જવાબઃ
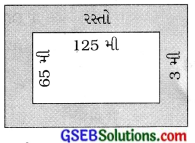 +
+
લંબચોરસ બાગની લંબાઈ (l) = 125 મી
લંબચોરસ બાગની પહોળાઈ (b) = 65 મી
∴ લંબચોરસ બાગનું ક્ષેત્રફળ = l × b
= 125 મી × 65 મી = 8125 મી2
આ બાગની ફરતે ચારે તરફ બહારની બાજુએ 3 મી પહોળાઈનો રસ્તો છે.
∴ રસ્તા સાથે બાગની લંબાઈ = (125 + 3 + 3) મી = 131 મી
રસ્તા સાથે બાગની પહોળાઈ = (65 + 3 + 3) મી = 71 મી
∴ રસ્તા સાથે લંબચોરસ બાગનું ક્ષેત્રફળ = લંબાઈ × પહોળાઈ
= 131 મી × 71 મી = 9301 મી2
હવે, રસ્તાનું ક્ષેત્રફળ = રસ્તા સાથે બાગનું ક્ષેત્રફળ – બાગનું ક્ષેત્રફળ
= 9301 મી2 – 8125 મી2 = 1176 મી2
આમ, રસ્તાનું ક્ષેત્રફળ 1176 મી2 હોય.
પ્રશ્ન 3.
8 સેમી લાંબા અને 5 સેમી પહોળા પૂઠા પર એક ચિત્ર દોરેલું છે. પૂંઠા પર ચિત્રની ફરતે અંદરની બાજુએ ચારે તરફ 1.5 સેમી હાંસિયો છોડેલો છે. આ હાંસિયાનું ક્ષેત્રફળ શોધો.
જવાબઃ
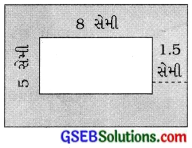
અહીં બહારનો લંબચોરસ એ હાંસિયા સાથેનો છે.
બહારના લંબચોરસની લંબાઈ (હાંસિયા સાથે) = 8 સેમી
બહારના લંબચોરસની પહોળાઈ (હાંસિયા સાથે) = 5 સેમી
∴ બહારના લંબચોરસનું ક્ષેત્રફળ = 8 સેમી × 5 સેમી = 40 સેમી2
અંદરના લંબચોરસની લંબાઈ = (8 સેમી – 1.5 સેમી – 1.5 સેમી) = 5 સેમી
અંદરના લંબચોરસની પહોળાઈ = (5 સેમી – 1.5 સેમી – 1.5 સેમી) = 2 સેમી
∴ અંદરના લંબચોરસનું ક્ષેત્રફળ = 5 સેમી × 2 સેમી = 10 સેમી2
∴ હાંસિયાનું ક્ષેત્રફળ = (બહારના લંબચોરસનું ક્ષેત્રફળ) – (અંદરના લંબચોરસનું ક્ષેત્રફળ)
= 40 સેમી2 – 10 સેમી2 = 30 સેમી2
આમ, હાંસિયાનું ક્ષેત્રફળ 30 સેમી2 છે.
![]()
4. 5.5 મી લાંબા અને 4 મી પહોળા ઓરડાની બહારની ચારે બાજુએ 2.25 મી પહોળો વરંડો બનાવેલ છે.
પ્રશ્ન (i)
વરંડાનું ક્ષેત્રફળ શોધો.
જવાબ:

ઓરડાની લંબાઈ = 5.5 મી
ઓરડાની પહોળાઈ = 4 મી
∴ ઓરડાનું ભોંયતળિયાનું ક્ષેત્રફળ = લંબાઈ × પહોળાઈ
= 5.5 મી × 4 મી = 22 મી2
હવે, ઓરડાની ચારે બાજુએ ફરતો 2.25 મી પહોળો વરંડો છે.
∴ બહારના લંબચોરસની લંબાઈ = (5.5 + 2.25 + 2.25) મી = 10 મી
અને બહારના લંબચોરસની પહોળાઈ = (4 + 2.25 + 2.25) મી = 8.5 મી
∴ બહારના લંબચોરસનું ક્ષેત્રફળ = લંબાઈ × પહોળાઈ
= 10 મી × 8.5 મી = 85 મી2
∴ વરંડાનું ક્ષેત્રફળ = બહારના લંબચોરસનું ક્ષેત્રફળ – અંદરના લંબચોરસનું ક્ષેત્રફળ
= 85 મી2 – 22 મી2 = 63 મી2
પ્રશ્ન (ii)
વરંડાના ભોયતળિયા પર ₹ 200 / મી2 પ્રમાણે સિમેન્ટ પાથરવાનો ખર્ શોધો.
જવાબ:
હવે સિમેન્ટ પાથરવાનો ખર્ચ ₹ 200 પ્રતિ મી2 છે.
સિમેન્ટ પાથરવાનો ખર્ચ = ₹ (200 × 63) = ₹ 12,600
5. 30 મી લંબાઈની બાજુવાળા ચોરસ બાગની અંદરની બાજુએ ચારે તરફ 1 મીટર પહોળો રસ્તો બનાવેલ છે.
પ્રશ્ન (i)
રસ્તાનું ક્ષેત્રફળ શોધો.
જવાબ:
ચોરસ બાગની લંબાઈ = 30 મી
∴ ચોરસ બાગનું ક્ષેત્રફળ = (લંબાઈ)2 = 30 મી × 30 મી = 900 મી2
આ ચોરસ બાગની અંદરના ભાગમાં ચારે તરફ ફરતો 1 મી પહોળાઈનો રસ્તો છે.
∴ અંદરના ચોરસની લંબાઈ = (30 – 1 – 1) મી = 28 મી
∴ અંદરના ચોરસનું ક્ષેત્રફળ = (લંબાઈ)2 = 28 મી × 28 મી
= 784 મી2
હવે, રસ્તાનું ક્ષેત્રફળ = બહારના ચોરસનું ક્ષેત્રફળ – અંદરના ચોરસનું ક્ષેત્રફળ
= 900 મી2 – 784 મી2 = 116 મી2
![]()
પ્રશ્ન (ii)
બાગના રસ્તા સિવાયના ભાગમાં ₹ 40 પ્રતિ મીટર2 પ્રમાણે ઘાસ ઉગાડવાનો ખર્ચ શોધો.
જવાબ:
બાગમાં રસ્તા સિવાયના ભાગમાં ઘાસ ઉગાડવું છે.
ઘાસ ઉગાડવાનો ખર્ચ ₹ 40 પ્રતિ મી2 છે.
∴ કુલ ખર્ચ = ₹ (40 × 784) = ₹ 31,360
આમ, રસ્તાનું ક્ષેત્રફળ 116 મી2 અને ઘાસ ઉગાડવાનો ખર્ચ ₹31,360 છે.
પ્રશ્ન 6.
700 મીટર લંબાઈ અને 300 મીટર પહોળાઈ ધરાવતા બાગની મધ્યમાંથી પસાર થતાં અને તેની બાજુઓને સમાંતર એવા 10 મી પહોળા બે પરસ્પર લંબ રસ્તા બનાવેલા છે. રસ્તાઓનું ક્ષેત્રફળ શોધો. રસ્તા સિવાયના બાગનું ક્ષેત્રફળ પણ શોધો. તમારા જવાબો હેક્ટરનાં માપમાં આપો.
જવાબઃ
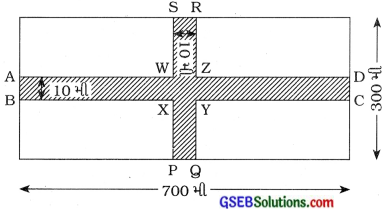
લંબચોરસ બાગની લંબાઈ = 700 મી
લંબચોરસ બાગની પહોળાઈ = 300 મી
લંબચોરસ બાગનું ક્ષેત્રફળ = લંબાઈ × પહોળાઈ
= 700 મી × 300 મી = 2,10,000 મી2
આ બાગમાં આકૃતિમાં બતાવ્યા પ્રમાણેના 10 મી પહોળાઈના બે રસ્તા છે.
આ રસ્તાનાં ક્ષેત્રફળ = (ABCDનું ક્ષેત્રફળ) + (PQRSનું ક્ષેત્રફળ) – (XYZWનું ક્ષેત્રફળ)
= (700 × 10) મી2 + (300 × 10) મી2 – (10 × 10) મી2
= 7000 મી2 + 3000 મી2 – 100 મી2
= 10,000 મી2 – 100 મી2 = 9900 મી2
હવે, 1 મી2 = \(\frac {1}{10,000}\) હેક્ટર
∴ 9900 મી2 = 0.99 હેક્ટર
હવે, બાગમાં રસ્તા સિવાયના ભાગનું ક્ષેત્રફળ = બાગનું ક્ષેત્રફળ – રસ્તાનું ક્ષેત્રફળ
= 2,10,000 મી2 – 9900 મી2 = 2,00,100 મી2
હવે, 1 મી2 = \(\frac {1}{10,000}\) હેક્ટર
∴ 2,00, 100 મી2 = 20.01 હેક્ટર
![]()
7. 90 મીટર લંબાઈ અને 60 મીટર પહોળાઈ ધરાવતા ખેતરના મધ્યમાંથી પસાર થતાં અને તેની બાજુઓને સમાંતર એવા 3 મીટર પહોળા બે પરસ્પર લંબ રસ્તા બનાવેલા છે.
પ્રશ્ન (i)
રસ્તાઓએ આવરેલું ક્ષેત્રફળ શોધો.
જવાબ:
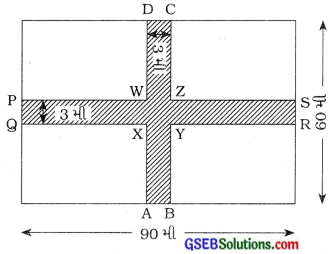
લંબચોરસ ખેતરની લંબાઈ = 90 મી
લંબચોરસ ખેતરની પહોળાઈ = 60 મી
આકૃતિમાં બતાવ્યા પ્રમાણે આ ખેતરમાં 3 મી પહોળાઈના બે રસ્તા
PQRS લંબચોરસ રસ્તાનું ક્ષેત્રફળ = 90 મી × 3 મી = 270 મી2
ABCD લંબચોરસ રસ્તાનું ક્ષેત્રફળ = 60 મી × 3 મી = 180 મી2
XYZW ચોરસ રસ્તાનું ક્ષેત્રફળ = 3 મી × 3 મી = 9 મી2
રસ્તાનાં ક્ષેત્રફળ = ☐ PQRSનું ક્ષેત્રફળ + ☐ ABCDનું ક્ષેત્રફળ – ☐ XYZWનું ક્ષેત્રફળ
= 270 મી2 + 180 મી2 – 9 મી2
= 450 મી2 – 9 મી2 = 441 મી2
પ્રશ્ન (ii)
₹ 110 / મી2 પ્રમાણે રસ્તાઓ બનાવવાનો ખર્ચ શોધો.
જવાબ:
1 મી2 રસ્તો બનાવવાનો ખર્ચ = 110
∴ 441 મી રસ્તો બનાવવાનો ખર્ચ = ₹ (110 × 441)
= ₹ 48,510
પ્રશ્ન 8.
પ્રજ્ઞાએ 4 સેમી ત્રિજ્યાવાળી એક વર્તુળાકાર નળીની ફરતે દોરી વીંટાળી (નીચેની આકૃતિ) અને જરૂરી લંબાઈની દોરી કાપી લીધી. હવે તેણે એ જ દોરીને 4 સેમીની બાજુ ધરાવતા ચોરસ ડબાની આસપાસ વીંટાળી (આકૃતિ જુઓ). શું તેની પાસે દોરી વધી હશે? (π = 3.14)
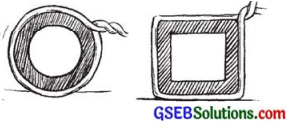
જવાબ:
વર્તુળાકાર નળીની ત્રિજ્યા (r) = 4 સેમી
∴ આ નળીનો પરિઘ = 2πr = 2 × 3.14 × 4 સેમી = 25.12 સેમી
આમ, નળીને ગોળ વીંટાળાતી દોરીની લંબાઈ 25.12 સેમી છે.
હવે, આ દોરીને ચોરસ ડબાની આસપાસ વીંટાળાય છે.
ચોરસ ડબાની બાજુની લંબાઈ 4 સેમી છે.
∴ ચોરસ ડબાની પરિમિતિ = 4 × 4 સેમી = 16 સેમી
આમ, ચોરસની આસપાસ દોરી વીંટાય છે તેની લંબાઈ 16 સેમી છે.
હવે, 25.12 સેમી > 16 સેમી તથા (25.12 – 16) સેમી = 9.12 સેમી
હા, ચોરસ ડબાને દોરી વીંટાળતાં પ્રજ્ઞા પાસે 9.12 સેમી દોરી બાકી વધી હશે.
![]()
પ્રશ્ન 9.
બાજુની આકૃતિમાં એક લંબચોરસ જમીન પરની લોનની મધ્યમાં ફૂલોનો એક વર્તુળાકાર બાગ દર્શાવેલો છે. (π = 3.14 લો.)
(i) બધી જમીનનું ક્ષેત્રફળ શોધો.
(ii) બાગનું ક્ષેત્રફળ શોધો.
(iii) બાગ સિવાયની જગ્યાનું ક્ષેત્રફળ શોધો.
(iv) બાગનો પરિઘ શોધો.
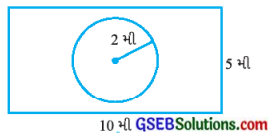
જવાબ:
લંબચોરસ જમીનની લંબાઈ 10 મી અને પહોળાઈ 5 મી છે.
(i) જમીનનું ક્ષેત્રફળ = લંબાઈ × પહોળાઈ
= 10 મી × 5 મી = 50 મી2
(ii) ફૂલના વર્તુળાકાર બાગની ત્રિજ્યા (r) = 2 મી
∴ ફૂલના વર્તુળાકાર બાગનું ક્ષેત્રફળ = πr2
= 3.14 × 2 × 2 = 12.56 મી2
(iii) જમીનમાં ફૂલોના બાગ સિવાયની જગ્યાનું ક્ષેત્રફળ
= 50 મી2 – 12.56 મી2
= 37.44 મી2
(iv) ફૂલોના વર્તુળાકાર બાગનો પરિઘ = 2πr
= 2 × 3.14 × 2 મી = 12.56 મી
પ્રશ્ન 10.
નીચેની આકૃતિઓમાં છાયાંકિત ભાગનું ક્ષેત્રફળ શોધો.
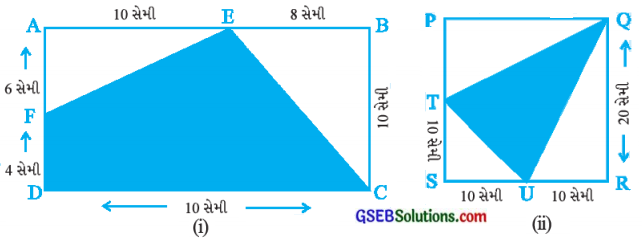
જવાબ:
(i) ABCD લંબચોરસની લંબાઈ (l) = 10 સેમી + 8 સેમી = 18 સેમી
અને પહોળાઈ (b) = 6 સેમી + 4 સેમી = 10 સેમી
લંબચોરસ ABCDનું ક્ષેત્રફળ = લંબાઈ × પહોળાઈ
= 18 સેમી × 10 સેમી = 180 સેમી2
∆AEFનું ક્ષેત્રફળ = \(\frac {1}{2}\) × પાયો × પાયા પરનો વેધ
= \(\frac {1}{2}\) × 6 × 10 = 30 સેમી2
∆CBEનું ક્ષેત્રફળ = \(\frac {1}{2}\) × પાયો × પાયા પરનો વેધ
= \(\frac {1}{2}\) × 8 × 10 = 40 સેમી2
હવે, છાયાંકિત ભાગનું ક્ષેત્રફળ = (ABCDનું ક્ષેત્રફળ) – (∆AEFનું ક્ષેત્રફળ + ∆CBEનું ક્ષેત્રફળ)
= (180 સેમી2) – (30 સેમી2 + 40 સેમી2)
= 180 સેમી2 – 70 સેમી2 = 110 સેમી2
આમ, છાયાંકિત ભાગનું ક્ષેત્રફળ 110 સેમી2 છે.
(ii) અહીં આપેલી આકૃતિ PQRS એ ચોરસ છે. ચોરસની બાજુની લંબાઈ = 20 સેમી
ચોરસ PQRSનું ક્ષેત્રફળ = (લંબાઈ)2
= 20 સેમી × 20 સેમી = 400 સેમી2
કાટકોણ ∆OPTનું ક્ષેત્રફળ = \(\frac {1}{2}\) × પાયો × પાયા પરનો વેધ
= \(\frac {1}{2}\) × 20 × 10 = 100 સેમી2
કાટકોણ ∆TSUનું ક્ષેત્રફળ = \(\frac {1}{2}\) × પાયો × પાયા પરનો વેધ
= \(\frac {1}{2}\) × 10 × 10 = 50 સેમી2
કાટકોણ ∆QRUનું ક્ષેત્રફળ = \(\frac {1}{2}\) × પાયો × પાયા પરનો વેધ
= \(\frac {1}{2}\) × 10 × 20 = 100 સેમી2
હવે, છાયાંકિત ભાગનું ક્ષેત્રફળ = (ચોરસ PQRSનું ક્ષેત્રફળ) – (∆QPTનું ક્ષેત્રફળ + ∆TSUનું ક્ષેત્રફળ + ∆QRUનું ક્ષેત્રફળ)
= (400 સેમી2) – (100 સેમી2 + 50 સેમી2 + 100 સેમી2)
= 400 સેમી2 – 250 સેમી2 = 150 સેમી2
આમ, છાયાંકિત ભાગનું ક્ષેત્રફળ 150 સેમી2 છે.
![]()
પ્રશ્ન 11.
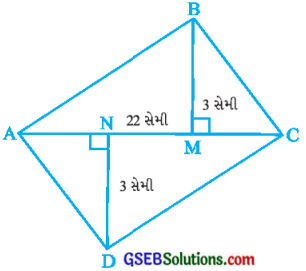
ચતુષ્કોણ ABCDનું ક્ષેત્રફળ શોધો.
અહીં, AC = 22 સેમી, BM = 3 સેમી, DN = 3 સેમી અને
\(\overline{\mathrm{BM}}\) ⊥ \(\overline{\mathrm{AC}}\) અને \(\overline{\mathrm{DN}}\) ⊥ \(\overline{\mathrm{AC}}\)
જવાબઃ
∆ABCનું ક્ષેત્રફળ
= \(\frac {1}{2}\) × AC × AC પરનો વેધ
= \(\frac {1}{2}\) × 22 × 3 = 33 સેમી2
∆ACDનું ક્ષેત્રફળ = \(\frac {1}{2}\) × AC × AC પરનો વેધ
= \(\frac {1}{2}\) × 22 × 3 = 33 સેમી2
ચતુષ્કોણ ABCDનું ક્ષેત્રફળ = ∆ABCનું ક્ષેત્રફળ + ∆ACDનું ક્ષેત્રફળ
= 33 સેમી2 + 33 સેમી2
= 66 સેમી2
આમ, ચતુષ્કોણ ABCDનું ક્ષેત્રફળ 66 સેમી2 છે.