GSEB Solutions Class 7 Maths Chapter 11 પરિમિતિ અને ક્ષેત્રફળ InText Questions

Gujarat Board GSEB Solutions Class 7 Maths Chapter 11 પરિમિતિ અને ક્ષેત્રફળ InText Questions and Answers.

Gujarat Board Textbook Solutions Class 7 Maths Chapter 11 પરિમિતિ અને ક્ષેત્રફળ InText Questions

પ્રયત્ન કરો: (પાઠ્યપુસ્તક પાન નંબર . 205)

1. નીચેના પ્રશ્નોના જવાબ શોધવા માટે તમારે શું શોધવું પડે – પરિમિતિ કે ક્ષેત્રફળ?

1. વર્ગમાંનું કાળું પાટિયું કેટલી જગ્યા રોકે છે?
2. ફૂલોના લંબચોરસ ક્યારાને ફરતેથી બંધ કરવા માટે કેટલી લંબાઈનો તાર જોઈશે?
3. એક ત્રિકોણાકાર બાગને ફરતે બે વાર આંટા મારવાથી તમે કેટલું અંતર કાપશો?
4. એક લંબચોરસ તરણકુંડને ઢાંકવા માટે તમારે કેટલી પ્લાસ્ટિકની શીટ જોઈશે?

જવાબ:

1. વર્ગમાંનું કાળું પાટિયું કેટલી જગા રોકે છે તે શોધવા માટે વર્ગમાંના કાળા પાટિયાનું ક્ષેત્રફળ શોધવું પડે.
2. ફૂલોના લંબચોરસ ક્યારાને ફરતેથી તાર વડે બંધ કરવા માટે ફૂલોના લંબચોરસ ક્યારાની પરિમિતિ શોધવી પડે.
3. એક ત્રિકોણાકાર બાગને ફરતે બે વાર આંટો મારવાથી કપાયેલું અંતર શોધવા માટે ત્રિકોણાકાર બાગની પરિમિતિ શોધીને 2 વડે ગુણવા પડે.
4. એક લંબચોરસ તરણકુંડને પ્લાસ્ટિકની શીટ વડે ઢાંકવા જરૂરી શીટ શોધવા લંબચોરસ તરણકુંડનું ક્ષેત્રફળ શોધવું પડે.

પ્રયત્ન કરો(પાઠ્યપુસ્તક પાન નંબર . 206)

1. આવા ઘણા આકારો અને કટિંગ્ઝ માટે આ પ્રયોગ કરો. તમે ચોરસ ખાનાવાળા કાગળ પર આ આકારો દોરી તેની પરિમિતિ અને ક્ષેત્રફળ ગણી શકો છો.

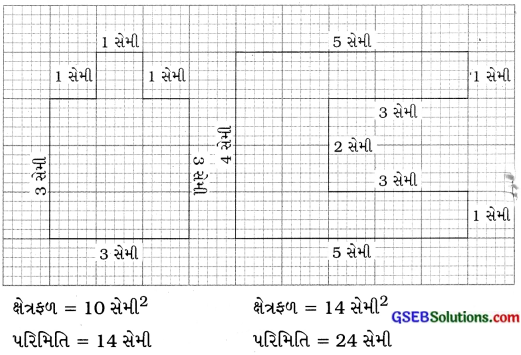
ક્ષેત્રફળ = 10 સેમી² પરિમિતિ = 14 સેમી²
ક્ષેત્રફળ = 14 સેમી પરિમિતિ = 24 સેમી
તમે જોયું છે કે પરિમિતિમાં વધારો થાય એનો અર્થ એ નથી કે ક્ષેત્રફળ વધશે.
જવાબ:
નીચે ઉદાહરણ દ્વારા સમજીએ કે હંમેશાં પરિમિતિ વધે તો ક્ષેત્રફળ વધે જ એવું નથી. અમુક સંજોગોમાં પરિમિતિ વધે તો ક્ષેત્રફળ ન પણ વધે.

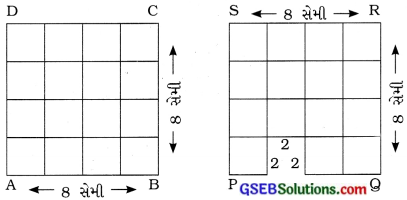
☐ABCDની પરિમિતિ = 2 (લંબાઈ + પહોળાઈ) = 2 (8 + 8) = 2 (16) = 32 સેમી
☐ABCDનું ક્ષેત્રફળ = લંબાઈ × લંબાઈ = 8 × 8 = 64 સેમી²
☐ABCDમાંથી 2 સેમીનો એક ચોરસ ટુકડો કાપી લઈએ. તો –
☐PQRSની પરિમિતિ = 32 સેમી + 4 સેમી = 36 સેમી
☐PQRSનું ક્ષેત્રફળ = 64 સેમી² – 4 સેમી² = 60 સેમી²
આથી, પરિમિતિ વધે તેમ ક્ષેત્રફળ વધે જ એવું હંમેશાં હોતું નથી.

2. પરિમિતિ વધવાની સાથે ક્ષેત્રફળ પણ વધે તેવાં બે ઉદાહરણો આપો.
જવાબ:
(i) ધારો કે, એક લંબચોરસની લંબાઈ 5 સેમી અને પહોળાઈ 4 સેમી છે.
લંબચોરસની પરિમિતિ = 2 (લંબાઈ + પહોળાઈ)
= 2 (5 + 4) સેમી = 18 સેમી
અને લંબચોરસનું ક્ષેત્રફળ = (લંબાઈ × પહોળાઈ)
= (5 × 4) સેમી² = 20² સેમી
હવે લંબચોરસની લંબાઈ અને પહોળાઈમાં 2 સેમીનો વધારો કરીએ.
લંબચોરસની લંબાઈ 7 સેમી અને પહોળાઈ 6 સેમી થશે.
લંબચોરસની પરિમિતિ = 2 (લંબાઈ + પહોળાઈ)
= 2 (7 + 6) સેમી
= 26 સેમી
લંબચોરસનું ક્ષેત્રફળ = (લંબાઈ × પહોળાઈ)
= (7 × 6) સેમી² = 42 સેમી²
આમ, પરિમિતિ વધે છે તેમ ક્ષેત્રફળ પણ વધે છે.

(ii) ધારો કે, એક ચોરસની લંબાઈ 4 સેમી છે.
ચોરસની પરિમિતિ = 4 (લંબાઈ) = 4 (4) = 16 સેમી²
અને ચોરસનું ક્ષેત્રફળ = (લંબાઈ × લંબાઈ)
= 4 × 4 સેમી² = 16 સેમી²
હવે ચોરસની લંબાઈમાં 2 સેમીનો વધારો કરીએ.
હવે ચોરસની બાજુની લંબાઈ 6 સેમી છે.
ચોરસની પરિમિતિ = 4 (લંબાઈ) = 4 (6) સેમી = 24 સેમી
ચોરસનું ક્ષેત્રફળ = (લંબાઈ × લંબાઈ) = 6 × 6 સેમી² = 36 સેમી²
આમ, પરિમિતિ વધે છે તેમ ક્ષેત્રફળ પણ વધે છે.

3. પરિમિતિ વધે પરંતુ ક્ષેત્રફળ ન વધે તેવાં બે ઉદાહરણો આપો.
જવાબ:
(i) ધારો કે, લંબચોરસની લંબાઈ 4 સેમી અને પહોળાઈ 3 સેમી છે.
∴ લંબચોરસનું ક્ષેત્રફળ = લંબાઈ × પહોળાઈ
= 4 × 3 સેમી² = 12 સેમી²
લંબચોરસની પરિમિતિ = 2 (લંબાઈ + પહોળાઈ)
= 2 (4 + 3) સેમી = 14 સેમી
ધારો કે લંબચોરસની લંબાઈ 6 સેમી અને પહોળાઈ 2 સેમી છે.
∴ લંબચોરસનું ક્ષેત્રફળ = લંબાઈ × પહોળાઈ
= 6 × 2 સેમી² = 12 સેમી²
લંબચોરસની પરિમિતિ = 2 (લંબાઈ + પહોળાઈ)
= 2 (6 + 2) સેમી = 16 સેમી
આમ, લંબચોરસની પરિમિતિ વધે છે પણ ક્ષેત્રફળ તેનું તે જ રહે છે.

(ii) ધારો કે, લંબચોરસની લંબાઈ 5 સેમી અને પહોળાઈ 4 સેમી છે.
∴ લંબચોરસનું ક્ષેત્રફળ = લંબાઈ × પહોળાઈ
= 5 × 4 સેમી² = 20 સેમી²
લંબચોરસની પરિમિતિ = 2 (લંબાઈ + પહોળાઈ)
= 2 (5 + 4) સેમી = 18 સેમી
ધારો કે, લંબચોરસની લંબાઈ 10 સેમી અને પહોળાઈ 2 સેમી છે. –
∴ લંબચોરસનું ક્ષેત્રફળ = લંબાઈ × પહોળાઈ
= 10 × 2 સેમી² = 20 સેમી²
લંબચોરસની પરિમિતિ = 2 (લંબાઈ + પહોળાઈ)
= 2 (10 + 2) સેમી = 24 સેમી
આમ, લંબચોરસની પરિમિતિ વધે છે પણ ક્ષેત્રફળ તેનું તે જ રહે છે.

પ્રયત્ન કરો (પાઠ્યપુસ્તક પાન નંબર . 210)

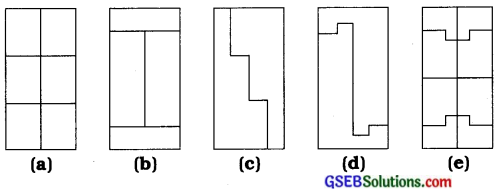
1. નીચે આપેલા દરેક લંબચોરસની લંબાઈ 6 સેમી અને પહોળાઈ 4 સેમી છે. તે દરેક એકરૂપ બહુકોણોથી બનેલા છે. દરેક બહુકોણનું ક્ષેત્રફળ શોધો.

જવાબ:
અહીં દરેક લંબચોરસની લંબાઈ l = 6 સેમી અને પહોળાઈ b = 4 સેમી
દરેક લંબચોરસનું ક્ષેત્રફળ = l × b = 6 × 4 સેમી² = 24 સેમી²
(a) આ આકૃતિમાં લંબચોરસને છ એકરૂપ બહુકોણમાં વિભાજિત કરેલ છે.
∴ દરેક બહુકોણનું ક્ષેત્રફળ = \(\frac {1}{6}\) × લંબચોરસનું ક્ષેત્રફળ
= \(\frac {1}{6}\) × 24 સેમી² = 4 સેમી²

(b) આ આકૃતિમાં લંબચોરસને ચાર એકરૂપ બહુકોણમાં વિભાજિત કરેલ છે.
∴ દરેક બહુકોણનું ક્ષેત્રફળ = \(\frac {1}{4}\) × લંબચોરસનું ક્ષેત્રફળ
= \(\frac {1}{4}\) × 24 સેમી² = 6 સેમી²

(c) આ આકૃતિમાં લંબચોરસને બે એકરૂપ બહુકોણમાં વિભાજિત કરેલ છે.
∴ દરેક બહુકોણનું ક્ષેત્રફળ = \(\frac {1}{2}\) × લંબચોરસનું ક્ષેત્રફળ
= \(\frac {1}{2}\) × 24 સેમી² = 12 સેમી²

(d) આ આકૃતિમાં લંબચોરસને બે એકરૂપ બહુકોણમાં વિભાજિત કરેલ છે.
∴ દરેક બહુકોણનું ક્ષેત્રફળ = \(\frac {1}{2}\) × લંબચોરસનું ક્ષેત્રફળ
= \(\frac {1}{2}\) × 24 સેમી² = 12 સેમી²

(e) આ આકૃતિમાં લંબચોરસને આઠ એકરૂપ બહુકોણમાં વિભાજિત કરેલ છે.
∴ દરેક બહુકોણનું ક્ષેત્રફળ = \(\frac {1}{8}\) × લંબચોરસનું ક્ષેત્રફળ
= \(\frac {1}{8}\) × 24 સેમી² = 3 સેમી²

પાઠ્યપુસ્તકમાંથી: (પાઠ્યપુસ્તક પાન નંબર . 211)

1. નીચેના સમાંતરબાજુ ચતુષ્કોણો જુઓ:

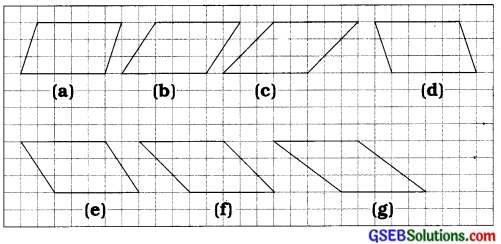
આ સમાંતરબાજુ ચતુષ્કોણોનાં ક્ષેત્રફળ, આકૃતિની અંદરના ભાગમાં આવેલા ચોરસની ગણતરી કરીને શોધો અને બાજુઓને માપીને તેની પરિમિતિ પણ શોધો. આપેલ કોષ્ટક પૂર્ણ કરોઃ
જવાબઃ

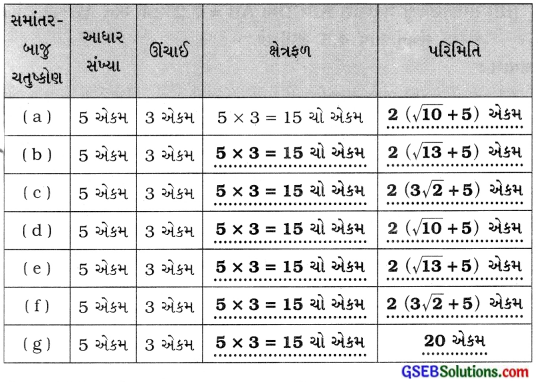
(a) આધાર = 5 એકમ, ઊંચાઈ = 3 એકમ
∴ ક્ષેત્રફળ = આધાર × ઊંચાઈ
= 5 × 3 = 15 ચો એકમ

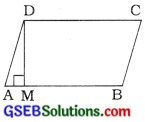
AD = \(\sqrt{\mathrm{DM}^{2}+\mathrm{AM}^{2}}\)
= \(\sqrt{3^{2}+1^{2}}\) = \(\sqrt{9+1}\) = \(\sqrt{10}\) એકમ
હવે, પરિમિતિ = 2 (AD + AB) = 2(\(\sqrt{10}\) + 5) એકમ
ઉપરની રીતે બધી આકૃતિઓનાં ક્ષેત્રફળ અને પરિમિતિ શોધી શકાય.
તમે જોશો કે આ બધા સમાંતરબાજુ ચતુષ્કોણોનાં ક્ષેત્રફળ સમાન છે પરંતુ તેમની પરિમિતિ ભિન્ન છે.

પ્રયત્ન કરો : (પાઠ્યપુસ્તક પાન નંબર . 212)

1. નીચેના સમાંતરબાજુ ચતુષ્કોણોનાં ક્ષેત્રફળ શોધોઃ

પ્રશ્ન (i)

જવાબ:
અહીં સમાંતરબાજુ ચતુષ્કોણનો પાયો b = 8 સેમી, ઊંચાઈ h = 3.5 સેમી
∴ સમાંતરબાજુ ચતુષ્કોણનું ક્ષેત્રફળ = b × h
= 8 × 3.5 સેમી² = 28 સેમી²

પ્રશ્ન (ii)

જવાબ:
અહીં સમાંતરબાજુ ચતુષ્કોણનો પાયો b = 8 સેમી, ઊંચાઈ h = 2.5 સેમી
∴ સમાંતરબાજુ ચતુષ્કોણનું ક્ષેત્રફળ = b × h
= 8 × 2.5 સેમી² = 20 સેમી²

પ્રશ્ન (iii)
સમાંતરબાજુ ચતુષ્કોણ ABCDમાં AB = 7.2 સેમી અને \(\overline{\mathbf{A B}}\) પર Cમાંથી દોરેલા લંબનું માપ 4.5 સેમી છે.
જવાબ:
અહીં સમાંતરબાજુ ચતુષ્કોણ ABCDનો પાયો AB = 7.2 સેમી અને ઊંચાઈ = 4.5 સેમી .
∴ સમાંતરબાજુ ચતુષ્કોણ ABCDનું ક્ષેત્રફળ = પાયો × ઊંચાઈ
= 7.2 સેમી × 4.5 સેમી
= 32.40 સેમી²

પ્રયત્ન કરો (પાઠ્યપુસ્તક પાન નંબર . 219)

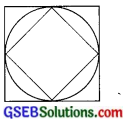
1. આકૃતિમાં –
(a) કયા ચોરસની પરિમિતિ વધુ છે?
(b) નાના ચોરસની પરિમિતિ અને વર્તુળનો પરિઘ એ બેમાંથી કયું માપ મોટું છે?

જવાબ:
(a) બંને ચોરસમાંથી અંદરના ચોરસ કરતાં બહારના ચોરસની પરિમિતિ વધારે છે.
(b) અંદરના નાના ચોરસની પરિમિતિ કરતાં વર્તુળનો પરિઘ વધારે છે.

આ કરો: (પાઠ્યપુસ્તક પાન નંબર . 219)

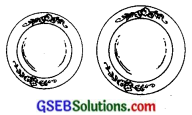
1. આકૃતિમાં બતાવ્યા પ્રમાણે એક નાની અને એક મોટી પ્લેટ લો. બંનેને ટેબલની સપાટી પર એક વાર ગબડાવો. એક ચક્રમાં કઈ પ્લેટ વધુ અંતર કાપે છે? ટેબલની આખી સપાટી પર ફરવામાં કઈ પ્લેટને ઓછા ચક્કર ફરવા પડશે?

જવાબ:
મોટી પ્લેટનો પરિઘ એ નાની પ્લેટના પરિઘ કરતાં વધારે હોય. તેથી એક ચક્ર પૂરું કરતાં નાની પ્લેટ કરતાં મોટી પ્લેટ વધુ અંતર કાપે. ટેબલની આખી સપાટી પર ફરવામાં મોટી પ્લેટને ઓછા ચક્કર ફરવા પડે.

પ્રયત્ન કરો (પાઠ્યપુસ્તક પાન નંબર . 222]

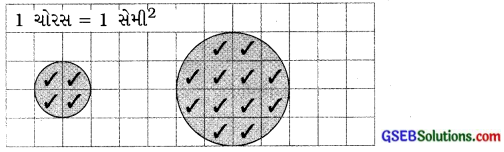
1. આલેખપત્ર પર ભિન્ન ત્રિજ્યાવાળાં વર્તુળો દોરો. વર્તુળની અંદરના ચોરસની સંખ્યા ગણીને ક્ષેત્રફળ શોધો. સૂત્રના ઉપયોગથી પણ ક્ષેત્રફળ ગણો. તમારા બંને જવાબો સરખાવો.

જવાબ:
1 સેમી ત્રિજ્યાનું અને 2 સેમી ત્રિજ્યાનું એવાં બે વર્તુળો આલેખપત્ર ઉપર દોરો.
નાના વર્તુળ માટે :
નાના વર્તુળનું ક્ષેત્રફળ = 4 પાનાં (∵ અર્ધ કરતાં મોટાને આખું ખાનું ગણતાં)
= 4 સેમી²
મોટા વર્તુળનું ક્ષેત્રફળ = 12 ખાનાં = 12 સેમી²
(∵ અર્ધ કરતાં મોટાને આખું ખાનું ગણતાં અને અર્ધ કરતાં નાના ખાનાં અવગણતાં)
હવે, સૂત્ર વડે ક્ષેત્રફળની ગણતરી કરીએ.
(1) નાના વર્તુળ માટે ત્રિજ્યા r = 1 સેમી
વર્તુળનું ક્ષેત્રફળ = πr²
= \(\frac {22}{7}\) × 1 × 1 = \(\frac {22}{7}\) = 3.14 સેમી² (આશરે)
મોટા વર્તુળ માટે ત્રિજ્યા r = 2 સેમી
વર્તુળનું ક્ષેત્રફળ = πr²
= \(\frac {22}{7}\) × 2 × 2 = \(\frac {22}{7}\) × 4 = \(\frac {88}{7}\)
= 12.57 સેમી² (આશરે)

પ્રયત્ન કરો: (પાઠ્યપુસ્તક પાન નંબર . 225)

1. નીચે આપેલાં માપોનું રૂપાંતર કરોઃ

પ્રશ્ન (i)
50 સેમી² ને મિમીમાં
જવાબ:
1 સેમી² = 100 મિમી²
∴ 50 સેમી² = (50 × 100) મિમી²
= 5000 મિમી

પ્રશ્ન (ii)
2 હેક્ટરને મી²માં
જવાબ:
1 હેક્ટર = 10,000 મી²
∴ 2 હેક્ટર = (2 × 10,000) મી²
= 20,000 મી²

પ્રશ્ન (iii)
10મી²ને સેમી²માં
જવાબ:
1 મી² = 10,000 સેમી²
∴ 10 મી = (10 × 10,000) સેમી²
= 1,00,000 સેમી²

પ્રશ્ન (iv)
1000 સેમી²ને મી² માં
જવાબ:
10,000 સેમી² = 1 મી²
∴ 1 સેમી² = \(\frac {1}{10,000}\) મી²
∴ 1000 સેમી² = (\(\frac {1}{10,000}\) × 1000) મી²
= \(\frac {1}{10}\)મી² = 0.1 મી²