Gujarat Board GSEB Solutions Class 8 Maths Chapter 10 ઘનાકારોનું પ્રત્યક્ષીકરણ Ex 10.3 Textbook Exercise Questions and Answers.
Gujarat Board Textbook Solutions Class 8 Maths Chapter 10 ઘનાકારોનું પ્રત્યક્ષીકરણ Ex 10.3
પ્રશ્ન 1.
શું કોઈ બહુફલકને આટલા ફલક હોઈ શકે?
(i) ત્રણ ત્રિકોણ
(ii) ચાર ત્રિકોણ
(iii) એક ચોરસ અને ચાર ત્રિકોણ
જવાબઃ
બહુલકને ચાર અથવા ચારથી વધુ ફલક હોય છે.
(i) બહુફલકને ત્રણ ત્રિકોણ ફલક હોય તે શક્ય નથી.
(ii) બહુલકને ચાર ત્રિકોણ ફલક હોઈ શકે. (ત્રિકોણીય પિરામિડ)
(iii) બહુફલકને એક ચોરસ અને ચાર ત્રિકોણ ફલક હોઈ શકે. (ચોરસ પાયાવાળો પિરામિડ)
![]()
પ્રશ્ન 2.
શું આપેલી કોઈ પણ સંખ્યાના ફલકથી બહુફલક બની શકે? (સૂચનઃ પિરામિડને ધ્યાનમાં રાખી વિચારો.)
જવાબઃ
હા, આપેલી ફલકની સંખ્યા 4 અથવા 4થી વધારે હોય, તો તેવા ફલકવાળો બહુલક બની શકે.
પ્રશ્ન 3.
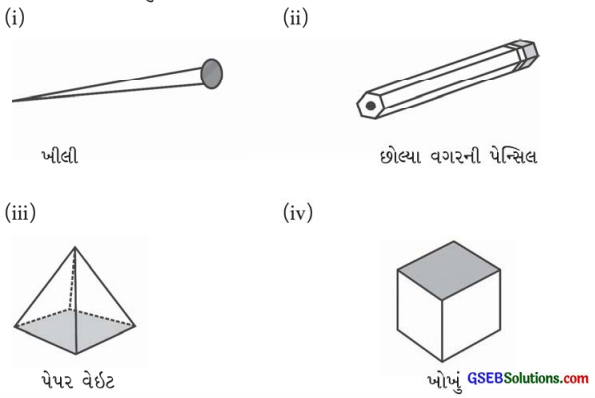
નીચેનામાંથી કઈ વસ્તુ પ્રિઝમ છે?
જવાબઃ
પ્રિઝમ એ એવો બહુફલક છે જેના પાયા તથા ઉપરના બે ફલક સમાંતર અને એકરૂપ બહુકોણ હોય અને બીજા ફલકો સમાંતરબાજુ ચતુષ્કોણ હોય.
(i) ખીલી એ પ્રિઝમ નથી.
(ii) છોલ્યા વગરની પેન્સિલ એ પ્રિઝમ છે.
(iii) પેપર વેઇટ એ પ્રિઝમ નથી. (પિરામિડ છે.)
(iv) ખોખું એ પ્રિઝમ છે.
![]()
4.
પ્રશ્ન (i)
પ્રિઝમ અને નળાકારમાં શું સામ્ય છે?
જવાબઃ
પ્રિઝમ અને નળાકાર બંનેમાં પાયો અને મથાળું એકરૂપ ફલકો હોય છે. વળી, આ બંને ફલકો એકબીજાને સમાંતર પણ હોય છે.
જો પ્રિઝમના પાયાની બાજુઓની સંખ્યા જેમ જેમ વધારતા જઈશું તેમ તેમ તેનો આકાર નળાકાર જેવો બનતો જાય છે.
પ્રશ્ન (ii)
પિરામિડ અને શંકુમાં શું સામ્ય છે?
જવાબઃ
પિરામિડ અને શંકુમાં સામ્યતા એ છે કે બંનેના બાજુના ફલકો ઉપરના ભાગમાં એક જ શિરોબિંદુમાં મળે છે. જો પિરામિડના પાયાની બાજુઓની સંખ્યા જેમ જેમ વધારતા જઈશું તેમ તેમ તેનો આકાર શંકુ જેવો બનતો જાય છે.
પ્રશ્ન 5.
શું ચોરસ પ્રિઝમ એ સમઘન જેવો જ હોય છે. સમજાવો.
જવાબઃ
ના, ચોરસ પ્રિઝમ એ હંમેશ સમઘન જેવો જ ન હોય. તે લંબઘન જેવો પણ હોઈ શકે.
પ્રશ્ન 6.
યુલર(Euler)નું સૂત્ર નીચેના ઘનાકાર માટે તપાસો:

જવાબ:
(i) આકૃતિ (i) માટે –
F = 7, V = 10 અને E = 15
∴ F + V = 7 + 70 = 17
હવે, F + V – E = 17 – 15 = 2
આમ, F + V – E = 2
આમ, યુલરનું સૂત્ર સાચું ઠરે છે.
(ii) આકૃતિ (ii) માટે –
F = 9, y = 9 અને E = 16
∴ F + V = 9 + 9 = 18
હવે, F + V – E = 18 – 16 = 2
આમ, F + V – E = 2
આમ, યુલરનું સૂત્ર સાચું ઠરે છે.
![]()
પ્રશ્ન 7.
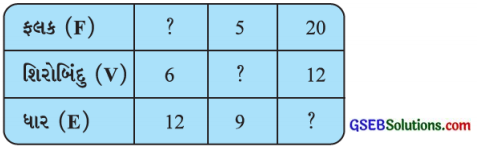
યુલર(Euler’s)ના સૂત્રનો ઉપયોગ કરી અજ્ઞાત સંખ્યા મેળવોઃ
જવાબ:
(i) અહીં F = ?, V = 6 અને E = 12
હવે, F + V – E = 2 (∵ યુલરનું સૂત્ર)
∴ F + 6 – 12 = 2
∴ F – 6 = 2.
∴ F = 2 + 6
∴ F = 8
(ii) અહીં F = 5, V = ? અને E = 9
હવે, F + V – E = 2 (∵ યુલરનું સૂત્ર)
∴ 5 + V – 9 = 2
∴ V – 4 = 2
∴ V = 2 + 4
∴ V = 6.
(iii) અહીં F = 20, V = 12 અને E = ?
હવે, F + V – E = 2 (∵ યુલરનું સૂત્ર)
∴ 20 + 12 – E = 2
∴ 32 – E = 2.
∴ – E = 2 – 32.
∴ – E = – 30
∴ E = 30.
![]()
પ્રશ્ન 8.
શું કોઈ બહુફલકને 10 ફલક (Faces), 20 ધાર (Edges) અને 15 શિરોબિંદુ Vertices) હોઈ શકે?
જવાબઃ
ઉપર આપેલ ફલક, ધાર અને શિરોબિંદુવાળો બહુલક ત્યારે જ હોઈ શકે જ્યારે આપેલ ફલક, ધાર અને શિરોબિંદુઓની સંખ્યા વડે યુલરનું સૂત્ર સાચું બનતું હોય.
અહીં F = 10, E = 20 અને V = 15
યુલરનું સૂત્ર F + V – E = 2 સંતોષાવું જોઈએ.
∴ F + V – E = 10 + 15 – 20
= 25 – 20
= 5
આમ, F + V – E ≠ 2
આમ, 10 ફલક, 20 ધાર અને 15 શિરોબિંદુવાળો બહુફલક ન હોઈ શકે.