GSEB Solutions Class 8 Maths Chapter 11 માપન Ex 11.2

Gujarat Board GSEB Solutions Class 8 Maths Chapter 11 માપન Ex 11.2 Textbook Exercise Questions and Answers.

Gujarat Board Textbook Solutions Class 8 Maths Chapter 11 માપન Ex 11.2

પ્રશ્ન 1.
એક ટેબલની ઉપર સમતલ પાટિયું સમલંબ ચતુષ્કોણ આકારનું છે. જો તેની સમાંતર બાજુઓની લંબાઈ 1 મીટર અને 1.2 મીટર હોય અને સમાંતર બાજુઓની વચ્ચેનું લંબઅંતર 0.8મી હોય, તો આ ટેબલના આ પાટિયાનું ક્ષેત્રફળ શોધો.

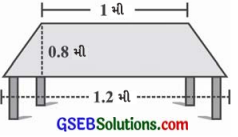
ઉત્તરઃ
સમલંબ ચતુષ્કોણનું ક્ષેત્રફળ
= \(\frac {1}{2}\) × સમાંતર બાજુઓનો સરવાળો × બે સમાંતર બાજુઓ વચ્ચેનું લંબઅંતર
= \(\frac {1}{2}\) × (1.2 + 1) × 0.8
= \(\frac {1}{2}\) × 2.2 × 0.8
= 0.88મી²
આમ, ટેબલના પાટિયાનું ક્ષેત્રફળ 0.88 મી²

પ્રશ્ન 2.
એક સમલંબ ચતુષ્કોણનું ક્ષેત્રફળ 34 સેમી² છે અને તેની ઊંચાઈ 4 સેમી છે. આ સમલંબની સમાંતર બાજુઓમાંથી એક બાજુની લંબાઈ 10 સેમી છે, તો તેની બીજી સમાંતર બાજુની લંબાઈ શોધો.

ઉત્તરઃ
ધારો કે આપેલા સમલંબ ચતુષ્કોણની બીજી સમાંતર બાજુની લંબાઈ x સેમી છે.
સમલંબ ચતુષ્કોણનું ક્ષેત્રફળ = \(\frac {1}{2}\) × (સમાંતર બાજુઓનો સરવાળો) × ઊંચાઈ
= \(\frac {1}{2}\) × (10 + x) × 4
= (10 + x) × 2 = 20 + 2x
પરંતુ સમલંબ ચતુષ્કોણનું ક્ષેત્રફળ 34 સેમી છે.
∴ 20 + 2x = 34
∴ 2x = 34 – 20
∴ 2x = 14
∴ x = 7
આમ, સમલંબ ચતુષ્કોણની બીજી સમાંતર બાજુની લંબાઈ 7 સેમી છે.

પ્રશ્ન 3.
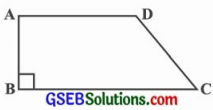
એક સમલંબ ચતુષ્કોણ આકારના ખેતર ABCD ની વાડની લંબાઈ 120 મીટર છે. જો BC = 48 મીટર, CD = 17 મીટર અને AD = 40 મીટર હોય, તો આ ખેતરનું ક્ષેત્રફળ શોધો. અહીં બાજુ AB એ સમાંતર બાજુ AD અને BC પર લંબ છે.

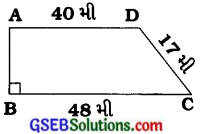
ઉત્તરઃ
ખેતરની પરિમિતિ = ખેતરની વાડની લંબાઈ
∴ AB + BC + CD + DA = 120
∴ AB + 48 + 17 + 40 = 120
∴ AB + 105 = 120
∴ AB = 120 – 105
∴ AB = 15 મી
હવે, સમલંબ ચતુષ્કોણ ABCDનું ક્ષેત્રફળ
= \(\frac {1}{2}\) × સમાંતર બાજુઓનો સરવાળો × સમાંતર બાજુઓ વચ્ચેનું લંબઅંતર
= \(\frac {1}{2}\) × (AD + BC) × AB
= \(\frac {1}{2}\) × (40 + 48) × 15
= \(\frac {1}{2}\) × 88 × 15
= 660 મી²
આમ, ખેતરનું ક્ષેત્રફળ 660 મી² થાય.

પ્રશ્ન 4.
એક ચતુષ્કોણ આકારના ખેતરના વિકર્ણની લંબાઈ 24 મીટર છે અને બાકીનાં બે શિરોબિંદુમાંથી આ વિકર્ણ પર દોરેલા લંબ 8 મીટર અને 13 મીટર છે, તો ખેતરનું ક્ષેત્રફળ શોધો.

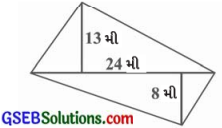
ઉત્તરઃ
ચતુષ્કોણ ABCDનું ક્ષેત્રફળ = ∆ ABDનું
ક્ષેત્રફળ + ∆ BCDનું ક્ષેત્રફળ
= \(\frac {1}{2}\) × BD x AM + \(\frac {1}{2}\) × BD × CN
= \(\frac {1}{2}\) × 24 × 13 + \(\frac {1}{2}\) × 24 × 8
= 12 × 13 + 12 × 8
= 156 + 96
= 252 મી²
આમ, ખેતરનું ક્ષેત્રફળ 252 મી² થાય.

પ્રશ્ન 5.
એક સમબાજુ ચતુષ્કોણના વિકર્ણોની લંબાઈ 7.5 સેમી અને 12 સેમી છે, તો તેનું ક્ષેત્રફળ શોધો.
ઉત્તરઃ
સમબાજુ ચતુષ્કોણનું ક્ષેત્રફળ = \(\frac {1}{2}\) × બે વિકર્ણોનો ગુણાકાર
= \(\frac {1}{2}\) × 7.5 × 12
= 7.5 × 6 = 45²
સેમી સમબાજુ ચતુષ્કોણનું ક્ષેત્રફળ 45 સેમી² છે.

પ્રશ્ન 6.
એક સમબાજુ ચતુષ્કોણની બાજુ 5 સેમી અને વેધ 4.8 સેમી છે, તો તેનું ક્ષેત્રફળ શોધો. જો એક વિકર્ણની લંબાઈ 8 સેમી હોય, તો બીજા વિકર્ણની લંબાઈ મેળવો.
ઉત્તરઃ

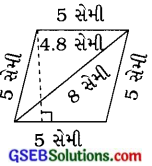
સમબાજુ ચતુષ્કોણ એ સમાંતરબાજુ ચતુષ્કોણ પણ છે.
સમબાજુ ચતુષ્કોણને સમાંતરબાજુ ચતુષ્કોણ તરીકે લઈ આપેલ માહિતી પરથી ક્ષેત્રફળ શોધીએ
સમાંતરબાજુ ચતુષ્કોણનું ક્ષેત્રફળ = પાયો × ઊંચાઈ
= 5 × 4.8
= 5 × 18
= 24 સેમી²
હવે, આ ચતુષ્કોણ સમબાજુ ચતુષ્કોણ છે જેનું ક્ષેત્રફળ 24 સેમી² છે.
સમબાજુ ચતુષ્કોણનું ક્ષેત્રફળ = \(\frac {1}{2}\) × વિકર્ણ 1 × વિકર્ણ 2
∴ 24 = \(\frac {1}{2}\) × 8 × વિકર્ણ 2
∴ 24 = 4 × વિકર્ણ 2
∴ વિકર્ણ 2 = \(\frac {24}{4}\) = 6 સેમી
આમ, સમબાજુ ચતુષ્કોણના બીજા વિકર્ણની લંબાઈ 6 સેમી છે.

પ્રશ્ન 7.
કોઈ મકાનના ભોંયતળિયામાં સમબાજુ ચતુષ્કોણ આકારની 3000 લાદીઓ , લગાડેલ છે. આ લાદીના વિકર્ણની લંબાઈ 45 સેમી અને 30 સેમી છે. હવે એક ચોરસ મીટર લાદી ઘસવાનો ખર્ચ જો 4 રૂપિયા હોય, તો સમગ્ર ભોંયતળિયાની લાદી ઘસાવવા માટે કેટલો ખર્ચ થશે?
ઉત્તરઃ
ભોયતળિયે લગાવવાની લાદી સમબાજુ ચતુષ્કોણાકાર છે. જેના વિકર્ણોની લંબાઈ 45 સેમી અને 30 સેમી છે.
એક લાદીનું ક્ષેત્રફળ = \(\frac {1}{2}\) × બે વિકર્ણોનો ગુણાકાર
= \(\frac {1}{2}\) × 45 × 30
= 45 × 15
= 675 સેમી²
હવે, કુલ લાદીની સંખ્યા 3000 છે.
∴ ભોંયતળિયાનું ક્ષેત્રફળ = એક લાદીનું ક્ષેત્રફળ × કુલ લાદી
= 675 × 3000
= 20,25,000 સેમી²
ભોંયતળિયાનું ક્ષેત્રફળ 20,25,000 સેમી² છે.
હવે, લાદી ઘસાવવાનો ખર્ચ મી²માં આપ્યો છે. તેથી 20,25,000 સેમી²ને મી²માં ફેરવીએ.
1 મીટર = 100 સેમી
∴ 1 મી² = 100 × 100 સેમી² = 10,000 સેમી²
20,25,000 સેમી² = \(\frac{2025000}{100 \times 100}\) મી² = \(\frac {2025}{10}\) મી²
જો એક ચોરસ મીટર લાદી ઘસાવવાનો ખર્ચ = 4 રૂપિયા
∴ ભોંયતળિયાની લાદી ઘસાવવાનો ખર્ચ = \(\frac {2025}{10}\) × 4
= ₹ 810
આમ, ભોંયતળિયાની લાદી ઘસાવવાનો ખર્ચ ₹ 810 થાય.

પ્રશ્ન 8.
મોહન એક સમલંબ ચતુષ્કોણ આકારનું ખેતર રસ્તો ખરીદવા ઇચ્છે છે. આ ખેતરની નદી તરફની બાજુ એ, રસ્તા તરફની બાજુને સમાંતર અને અંતરમાં બમણી છે. જો આ ખેતરનું ક્ષેત્રફળ 10,500 મી² હોય અને ખેતરની સમાંતર બાજુઓ વચ્ચેનું લંબઅંતર 100 મીટર હોય, તો ખેતરની નદી તરફની બાજુઓની લંબાઈ શોધો.

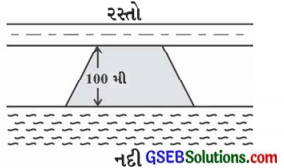
ઉત્તરઃ
આ સમલંબ ચતુષ્કોણાકાર ખેતરની નદી તરફની બાજુ એ, રસ્તા તરફની બાજુ કરતાં બમણા માપની છે.
ધારો કે રસ્તા તરફની બાજુની લંબાઈ x મીટર છે.
નદી તરફની બાજુની લંબાઈ 2x મીટર હોય.
સમલંબ ચતુષ્કોણાકાર ખેતરનું ક્ષેત્રફળ = \(\frac {1}{2}\) × (સમાંતર બાજુઓનો સરવાળો) × સમાંતર બાજુઓ વચ્ચેનું લંબઅંતર
= \(\frac {1}{2}\) × (x + 2x) × 100
= 3x × 50
= 150 × મી²
પણ ખેતરનું ક્ષેત્રફળ 10,500 મી² છે.
∴ 150 x = 10,500
∴ x = \(\frac {10500}{150}\)
∴ x = 70 મી
આમ, રસ્તા તરફની ખેતરની લંબાઈ 70 મીટર હોય.
નદી તરફના રસ્તાની લંબાઈ તેનાથી બમણી છે.
∴ નદી તરફના રસ્તાની લંબાઈ = 2 × 70 મીટર = 140 મીટર

પ્રશ્ન 9.
જમીનથી ઉપર ઊઠેલ એક ઓટલો છે. તેની ઉપરનું સમતલ સમબાજુ અષ્ટકોણ આકારનું છે. જે આકૃતિમાં દર્શાવેલ છે. આ અષ્ટકોણીય સમતલનું ક્ષેત્રફળ શોધો.

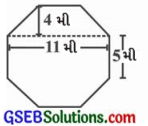
ઉત્તરઃ
અહીં સમબાજુ અષ્ટકોણનું આકૃતિમાં દર્શાવ્યા પ્રમાણે બે સમલંબ ચતુષ્કોણ અને એક લંબચોરસમાં વિભાજન થાય છે.
અહીં અષ્ટકોણાકાર ઓટલાની બધી બાજુઓનાં માપ સરખાં છે.
સમલંબની બે સમાંતર બાજુઓ 11 મી અને 5 મી તથા ઊંચાઈ 4 મી છે.
એક સમલંબ ચતુષ્કોણનું ક્ષેત્રફળ = \(\frac {1}{2}\) × (11 + 5) × 4
= 16 × 2
= 32 મી²
∴ બે સમલંબ ચતુષ્કોણનાં ક્ષેત્રફળ = 2 × 32 મી² = 64 મી²
લંબચોરસનું ક્ષેત્રફળ = લંબાઈ × પહોળાઈ
= 11 × 5
= 55 મી²
આમ, અષ્ટકોણ આકારના ઓટલાનું ક્ષેત્રફળ = 64 મી² + 55 મીટ²
= 119 મી²

પ્રશ્ન 10.
એક પંચકોણ આકારનો બગીચો છે જે આકૃતિમાં દર્શાવેલ છે. આ પંચકોણનું ક્ષેત્રફળ શોધવા માટે જ્યોતિ અને કવિતાએ જુદી જુદી રીતે પંચકોણને વિભાજિત કરેલ છે.

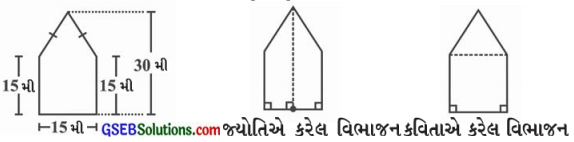
બંને રીતે કરેલા વિભાજનની મદદથી બગીચાનું ક્ષેત્રફળ શોધો. શું તમે આ પંચકોણનું ક્ષેત્રફળ શોધવાની અન્ય કોઈ રીત બતાવી શકો છો?
ઉત્તરઃ
જ્યોતિએ કરેલ વિભાજન જ્યોતિએ બનાવેલ આકૃતિ બે એકરૂપ (સમક્ષેત્ર) સમલંબ ચતુષ્કોણમાં વિભાજિત છે.
સમલંબ ચતુષ્કોણનું ક્ષેત્રફળ = \(\frac {1}{2}\) × સમાંતર બાજુઓનો સરવાળો × સમાંતર બાજુઓ વચ્ચેનું લંબઅંતર
= \(\frac {1}{2}\) × (15 + 30) × \(\frac {15}{2}\)
= \(\frac {1}{2}\) × 45 × \(\frac {15}{2}\)
= \(\frac {675}{4}\) મી²
∴ બે સમલંબ ચતુષ્કોણનું ક્ષેત્રફળ = 2 × \(\frac {675}{4}\) = \(\frac {675}{2}\) = 337.5 મી²
∴ જ્યોતિની રીતનો ઉપયોગ કરતાં પંચકોણીય આકૃતિનું ક્ષેત્રફળ = 337.5 મી²

કવિતાએ કરેલ વિભાજન:
કવિતાએ બનાવેલ આકૃતિ એક ચોરસ અને એક ત્રિકોણમાં વિભાજિત છે.
ચોરસનું ક્ષેત્રફળ = લંબાઈ × લંબાઈ = 15 × 15
= 225 મી²
ત્રિકોણનું ક્ષેત્રફળ = \(\frac {1}{2}\) × પાયો × પાયા ઉપરનો વેધ
= \(\frac {1}{2}\) × 15 × 15
= \(\frac {225}{2}\) = 112.5 મી²
∴ કવિતાની રીતનો ઉપયોગ કરતાં પંચકોણીય આકૃતિનું ક્ષેત્રફળ
= ચોરસનું ક્ષેત્રફળ + ત્રિકોણનું ક્ષેત્રફળ
= 225 મી² + 112.5 મી²
= 337.5 મી²

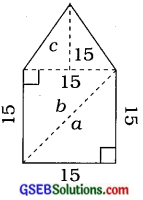
પંચકોણીય આકૃતિનું ક્ષેત્રફળ શોધવાની અન્ય રીતઃ
આકૃતિનું ત્રણ ત્રિકોણોમાં વહેંચણી કરીને –
∆ aનું ક્ષેત્રફળ = \(\frac {1}{2}\) × 15 × 15 = \(\frac {225}{2}\) = 112.5 મી²
∆ bનું ક્ષેત્રફળ = \(\frac {1}{2}\) × 15 × 18 = \(\frac {225}{2}\) = 112.5 મી²
∆ cનું ક્ષેત્રફળ = \(\frac {1}{2}\) × 15 × 15 = \(\frac {225}{2}\) = 112.5 મી²
પંચકોણીય આકૃતિનું ક્ષેત્રફળ = 112.5 મી² + 112.5 મી² + 112.5 મી²
= 337.5 મી²
આમ, પંચકોણીય આકૃતિનું ક્ષેત્રફળ 337.5 મી²

પ્રશ્ન 11.
આકૃતિમાં બતાવેલ ફોટો ફ્રેમની બહારની ધારનું માપ 24 સેમી × 28 સેમી છે અને અંદરની ધારનું માપ અનુક્રમે 16 સેમી × 20 સેમી છે. હવે જો ફેમના ચારે ટુકડાની જાડાઈ સમાન હોય, તો ફ્રેમના પ્રત્યેક ટુકડાનું ક્ષેત્રફળ શોધો.

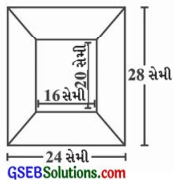
ઉત્તરઃ
ફોટો ફ્રેમનું ચાર સમલંબ ચતુષ્કોણમાં વિભાજન થાય છે. જેવા કે, a, b, c અને d.
વળી સામસામેના સમલંબ ચતુષ્કોણનાં માપ સરખા હોઈ તેમનાં ક્ષેત્રફળ સરખાં મળે.
∴ aનું ક્ષેત્રફળ = cનું ક્ષેત્રફળ તથા bનું ક્ષેત્રફળ = dનું ક્ષેત્રફળ

સમલંબ ચતુષ્કોણ વ માટે:
સમાંતર બાજુઓની લંબાઈ 24 સેમી અને 16 સેમી છે.
તથા ઊંચાઈ = \(\frac{28-20}{2}=\frac{8}{2}\) = 4 સેમી
સમલંબ ચતુષ્કોણ વનું ક્ષેત્રફળ = \(\frac {1}{2}\) × સમાંતર બાજુઓનો સરવાળો × સમાંતર બાજુઓ વચ્ચેનું લંબઅંતર
= \(\frac {1}{2}\) × (16 + 24) × 4
= \(\frac {1}{2}\) × 40 × 4 = 80 સેમી²
∴ સમલંબ ચતુષ્કોણ aનું ક્ષેત્રફળ 80 સેમી²
∴ સમલંબ ચતુષ્કોણ cનું ક્ષેત્રફળ 80 સેમી²

સમલંબ ચતુષ્કોણ b માટે:
સમાંતર બાજુઓની લંબાઈ 28 સેમી અને 20 સેમી છે.
તથા ઊંચાઈ = \(\frac{24-16}{2}=\frac{8}{2}\) = 4 સેમી
સમલંબ ચતુષ્કોણ નું ક્ષેત્રફળ = \(\frac {1}{2}\) × સમાંતર બાજુઓનો સરવાળો × સમાંતર બાજુઓ વચ્ચેનું લંબઅંતર
= \(\frac {1}{2}\) × (28 + 20) × 4
= \(\frac {1}{2}\) × 48 × 4 = 96 સેમી²
∴ સમલંબ ચતુષ્કોણ નું ક્ષેત્રફળ 96 સેમી²
∴ સમલંબ ચતુષ્કોણ તેનું ક્ષેત્રફળ 96 સેમી²