GSEB Solutions Class 8 Maths Chapter 13 સમપ્રમાણ અને વ્યસ્ત પ્રમાણ Ex 13.1

Gujarat Board GSEB Solutions Class 8 Maths Chapter 13 સમપ્રમાણ અને વ્યસ્ત પ્રમાણ Ex 13.1 Textbook Exercise Questions and Answers.

Gujarat Board Textbook Solutions Class 8 Maths Chapter 13 સમપ્રમાણ અને વ્યસ્ત પ્રમાણ Ex 13.1

પ્રશ્ન 1.
એક રેલવે-સ્ટેશન પર કાર પાર્કિંગનો દર નીચે પ્રમાણે છે :
4 કલાક ₹ 60
12 કલાક ₹ 140
8 કલાક ₹ 100
24 કલાક ₹ 180
ઉપરોક્ત પાર્કિંગના દર તેમને અનુરૂપ સમય સાથે સમપ્રમાણમાં છે કે નહીં તે ચકાસો.
ઉત્તરઃ
અહીં પાર્કિંગનો દર અને અનુરૂપ સમયનો ગુણોત્તર નીચે પ્રમાણે મળે :

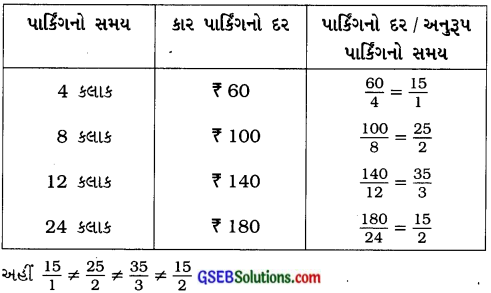
એટલે કે જુદા જુદા સમય માટે પાર્કિંગનો દર / અનુરૂપ પાર્કિંગના સમયનો ગુણોત્તર સરખો નથી.
ના, આમ, પાર્કિંગનો દર તેમને અનુરૂપ સમય સાથે સમપ્રમાણમાં નથી.

પ્રશ્ન 2.
એક રંગના મૂળ મિશ્રણના 8 ભાગમાં, 1 ભાગ લાલ રંગ મેળવીને મિશ્રણ તૈયાર કરેલ છે. નીચેના કોષ્ટકમાં મૂળ મિશ્રણનો ભાગ શોધોઃ
ઉત્તરઃ

લાલ રંગ	1	4	7	12	20
મૂળ મિશ્રણ	8	–	–	–	–

અહીં રંગના મૂળ મિશ્રણના 8 ભાગમાં 1 ભાગ લાલ રંગ મેળવવામાં આવે છે.
જો લાલ રંગનો ભાગ અનુક્રમે , x₁, x₂, x₃, x₄ અને x₅ હોય, તો તેના પ્રમાણમાં મૂળ મિશ્રણ y₁, y₂, y₃, y₄ અને y₅ હોય.
અહીં મિશ્રણ મેળવવાનું પ્રમાણ એ સમપ્રમાણ છે તે સ્પષ્ટ છે.

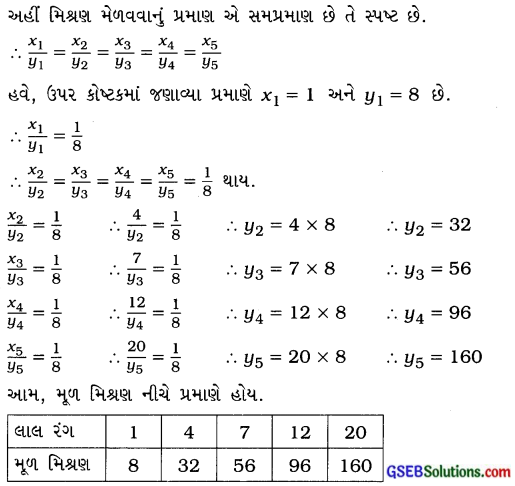
પ્રશ્ન 3.
પ્રશ્ન 2 માં, જો લાલ રંગના પદાર્થના 1 ભાગ માટે 75 મિલિ મૂળ મિશ્રણ જોઈએ, તો 1800 મિલિ મૂળ મિશ્રણમાં કેટલા ભાગનો લાલ રંગનો પદાર્થ જોઈશે?
ઉત્તરઃ
પ્રશ્ન 2 પ્રમાણે જોતાં –
x₁ = 1, y₁ = 75, x₂ = ? અને y₂ = 1800

આમ, 24 ભાગનો લાલ રંગનો પદાર્થ જોઈશે.

પ્રશ્ન 4.
ઠંડાં પીણાં બનાવતી એક ફેક્ટરીમાં, એક યંત્ર 6 કલાકમાં 840 બૉટલ ભરે છે, તો આ યંત્ર 5 કલાકમાં કેટલી બૉટલ ભરશે?
ઉત્તરઃ
ધારો કે, 5 કલાકમાં મશીન દ્વારા x બૉટલ ઠંડું પીણું ભરાય છે.

લાગતો સમય (કલાકમાં) (x)	6	5
ભરાતી ઠંડાં પીણાંની બૉટલ (y)	840	?

અહીં રકમ પરથી સ્પષ્ટ છે કે જેમ સમય વધે તેમ ઠંડાં પીણાંની બૉટલ વધુ ભરાય અને જેમ સમય ઘટે તેમ ઠંડાં પીણાની બૉટલ ઓછી ભરાય.
એટલે કે અહીં સમપ્રમાણ છે.
અહીં x₁ = 6, y₁ = 840, x₂ = 5 અને y₂ = ?
\(\frac{x_{1}}{y_{1}}=\frac{x_{2}}{y_{2}}\)
∴ \(\frac{6}{840}=\frac{5}{y_{2}}\)
∴ y₂ = \(\frac{5 \times 840}{6}\)
∴ y₂ = 700
આમ, આ યંત્ર 700 બોટલ ઠંડું પીણું ભરશે.

પ્રશ્ન 5.
એક જીવાણુ (bacteria)ના ચિત્રને 50,000 ગણું મોટું કરતા તેની લંબાઈ 5 સેમી થાય છે. જે આકૃતિમાં બતાવેલ છે, તો આ જીવાણુની વાસ્તવિક લંબાઈ કેટલી હશે? હવે જો ચિત્રને 20,000 ગણું કરવામાં આવે તો તેની લંબાઈ શોધો.
ઉત્તરઃ

બૅક્ટરિયાના ચિત્રમાં થતો વધારો	લંબાઈ (સેમીમાં)
50,000 ગણું મોટું (x1)	5 (y1)
1 (x2)	? (y2)

બૅક્ટરિયાના ચિત્રને જેટલું મોટું કરીએ તેટલી તેની લંબાઈ વધે છે.
એટલે અહીં સમપ્રમાણ છે.
\(\frac{x_{1}}{y_{1}}=\frac{x_{2}}{y_{2}}\)
∴ \(\frac{50000}{5}=\frac{1}{y_{2}}\)
∴ y₂ = \(\frac {5}{50000}\)
∴ y₂ = \(\frac {1}{10000}\)
∴ y₂ = 10^-4
આમ, આ જીવાણુની વાસ્તવિક લંબાઈ 10^-4 સેમી હશે.
હવે, ચિત્રને 20,000 ગણું મોટું કરવામાં આવે છે.

બૅક્ટરિયાના ચિત્રમાં થતો વધારો	લંબાઈ (સેમીમાં)
50,000 ગણું મોટું (x1)	5 (y1)
20,000 ગણું મોટું (x2)	? (y2)

\(\frac{x_{1}}{y_{1}}=\frac{x_{2}}{y_{2}}\)
∴ \(\frac{50000}{5}=\frac{20000}{y_{2}}\)
∴ y₂ = \(\frac{20000 \times 5}{50000}\)
∴ y₂ = 2
આમ, બૅક્ટરિયાની લંબાઈ 2 સેમી હોય.

પ્રશ્ન 6.
એક વહાણની પ્રતિકૃતિમાં તેના કૂવાતંભની ઊંચાઈ ૭ સેમી છે અને વાસ્તવિક વહાણમાં તેની ઊંચાઈ 12 મીટર છે. હવે જો વહાણની લંબાઈ 28 મીટર હોય, તો તેની પ્રતિકૃતિની લંબાઈ શોધો.
ઉત્તરઃ
નોંધઃ પ્રતિકૃતિ એટલે ચિત્ર.

–	વાસ્તવિક વહાણમાં	પ્રતિકૃતિમાં
વહાણની લંબાઈ	28 મીટર	?
કૂવાતંભની ઊંચાઈ	12 મીટર	9 સેમી

અહીં રકમ પ્રમાણે સ્પષ્ટ છે કે વહાણની લંબાઈ અને વાસ્તંભની ઊંચાઈ સમપ્રમાણમાં છે.
x₁ = 28, y₁ = 12, x₂ = ?, y₂ = 9
\(\frac{x_{1}}{y_{1}}=\frac{x_{2}}{y_{2}}\)
∴ \(\frac{28}{12}=\frac{x_{2}}{9}\)
∴ x₂ = \(\frac{28 \times 9}{12}\)
∴ x₂ = 21
આમ, પ્રતિકૃતિમાં કૂવાસ્તંભની ઊંચાઈ 21 સેમી છે.

પ્રશ્ન 7.
જો 2 કિગ્રા ખાંડમાં રહેલા સ્ફટિકોની સંખ્યા 9 × 10⁶ છે, તો નીચે દર્શાવેલ જથ્થામાં કેટલા સ્ફટિકો હશે?

પ્રશ્ન (i)
5 કિગ્રા
ઉત્તરઃ

ખાંડનું વજન અહીં	ખાંડના સ્ફટિકોની સંખ્યા
2	9 × 106
5	?

અહીં ખાંડનું વજન વધારે તેમ ખાંડના સ્ફટિકોની સંખ્યા વધારે હોય. એટલે કે અહીં સમપ્રમાણ છે.

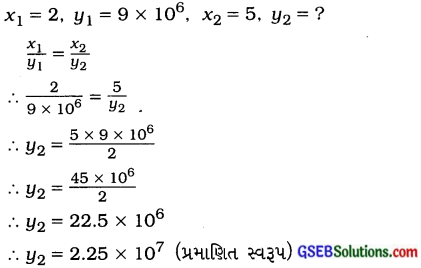
આમ, 5 કિગ્રા ખાંડમાં 2.25 × 10⁷ ખાંડના સ્ફટિકો હોય.

પ્રશ્ન (ii)
1.2 કિગ્રા
ઉત્તરઃ
1.2 કિલોગ્રામ ખાંડમાં ખાંડના સ્ફટિક કેટલા હશે તે શોધીએ.

ખાંડનું વજન અહીં	ખાંડના સ્ફટિકોની સંખ્યા
2	9 × 106
1.2	y2

અહીં x₁ = 2, y₁ = 9 × 10⁶, x₂ = 1.2, y₂ = ?
\(\frac{x_{1}}{y_{1}}=\frac{x_{2}}{y_{2}}\)
∴ \(\frac{2}{9 \times 10^{6}}=\frac{1.2}{y_{2}}\)
∴ y₂ = \(\frac{1.2 \times 9 \times 10^{6}}{2}\)
∴ y₂ = 0.6 × 9 × 10⁶
∴ y₂ = 5.4 × 10⁶
આમ, 1.2 કિગ્રા ખાંડમાં 5.4 × 10⁶ ખાંડના સ્ફટિકો હોય.

પ્રશ્ન 8.
રશ્મિ પાસે, 1 સેમી બરાબર 18 કિમી પ્રમાણમાપ ધરાવતો એક સડક માર્ગનો નકશો છે. હવે જો તે આ સડક પર 72 કિમીનું અંતર કાપે છે, તો તેના દ્વારા કાપેલ અંતર નકશામાં કેટલું દર્શાવ્યું હોય?

રોડ ઉપર ખરેખર કપાતું અંતર (કિમીમાં)	નકશામાં રજૂ થતું અંતર (સેમીમાં)
18	1
72	?

અહીં રોડ ઉપર ખરેખર કપાતું અંતર વધે, તો નકશામાં રજૂ થતું અંતર પણ વધે છે. તેથી સમપ્રમાણ છે.
અહીં x₁ = 18 કિમી, y₁ = 1 સેમી, x₂ = 72 કિમી, y₂ = ?
\(\frac{x_{1}}{y_{1}}=\frac{x_{2}}{y_{2}}\)
∴ \(\frac{18}{1}=\frac{72}{y_{2}}\)
∴ y₂ = \(\frac{72 \times 1}{18}\)
∴ y₂ = 4
આમ, નકશામાં દર્શાવેલું અંતર 4 સેમી હોય.

પ્રશ્ન 9.
એક 5 મીટર 60 સેમી ઊંચા શિરોલંબ થાંભલાના પડછાયાની લંબાઈ 3 મીટર 30 સેમી છે. આ જ સમયે

પ્રશ્ન (i)
10 મીટર 50 સેમી ઊંચા થાંભલાના પડછાયાની લંબાઈ શોધો.
ઉત્તરઃ

થાંભલાની પડછાયાની લંબાઈ	થાંભલાના પડછાયાની લંબાઈ
5 મીટર 60 સેમી = 560 સેમી	3 મીટર 20 સેમી = 320 સેમી
10 મીટર 50 સેમી = 1050 સેમી	?

થાંભલાની ઊંચાઈ જેમ વધે તેમ પડછાયાની લંબાઈ પણ વધે.
તેથી અહીં સમપ્રમાણ છે.
x₁ = 560, y₁ = 320, x₂ = 1050, y₂ = ?

પ્રશ્ન (ii)
5 મીટર લંબાઈનો પડછાયો હોય તેવા થાંભલાની ઊંચાઈ શોધો.
ઉત્તરઃ

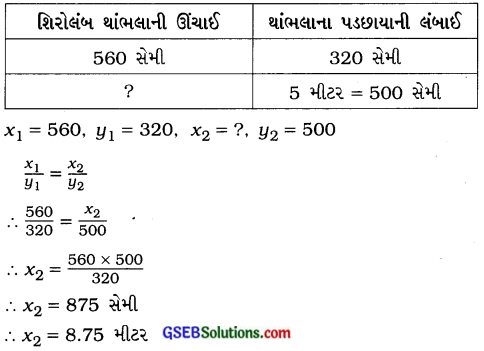
આમ, શિરોલંબ થાંભલાની ઊંચાઈ 8.75 મીટર એટલે કે 8 મીટર 75 સેમી હોય.

પ્રશ્ન 10.
એક ભારવાહક ખટારો 25 મિનિટમાં 14 કિમી અંતર કાપે છે. આ જ ઝડપે ગતિ કરે તો 5 કલાકમાં કેટલું અંતર કાપશે?
ઉત્તરઃ

અંતર (કિમીમાં)	સમય (મિનિટમાં)
14	25
?	5 કલાક = 300

અહીં જેમ સમય વધે તેમ ખટારો વધુ અંતર કાપે માટે સમપ્રમાણ છે.

ખટારો 168 કિમી અંતર કાપશે.