GSEB Solutions Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.4

Gujarat Board GSEB Solutions Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.4 Textbook Questions and Answers.

Gujarat Board Textbook Solutions Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.4

Question 1.
Find the surface area of a sphere of radius:
1. 10.5 cm
2. 5.6 cm
3. 14 cm
Solution:
1. r = 10.5 cm
∴ Surface area = 41πr²
= 4 x \(\frac {22}{7}\) x (10.5)²
= 1386 cm²

2. r = 5.6 cm
∴ Surface area = 4m²
= 4x \(\frac {22}{7}\) x (5.6)²
= 394.24 cm²

3. r = 14 cm
∴ Surface area = 4πr²
= 4 x \(\frac {22}{7}\) x (14)² = 2464 cm²

Question 2.
Find the surface area of a sphere of diameter:
1. 14 cm
2. 21 cm
3. 3.5 m
Solution:
1. Diameter = 14 cm
∴ Radius (r) = \(\frac {14}{2}\) cm = 7 cm
∴ Surface area = 4πr²
= 4 x \(\frac {22}{7}\) x (7)² = 616 cm²

2. Diameter = 21 cm
∴ Radius (r) = \(\frac {21}{2}\)cm
∴ Surface area = 4πr²
= 4 x \(\frac {22}{7}\) x (\(\frac {22}{7}\))²
= 1386 cm²

3. Diameter = 3.5 m
∴ Radius (r) = \(\frac {3.5}{2}\) m = 1.75 m
∴ Surface area = 4πr²
= 4 x \(\frac {22}{7}\) x (1.75)²
= 38.5 m²

Question 3.
Find the total surface area of a hemisphere of radius 10 cm. (Use π = 3.14)
Solution:
r = 10 cm
∴ Total surface area of the hemisphere
= 3πr² = 3 x 3.14 x (10)²
= 942 cm²

Question 4.
The radius of a spherical balloon increases from 7 cm to 14 cm as air is being pumped into it. Find the ratio of surface areas of the balloon in the two cases.
Solution:
Case I:
r = 7 cm
Surface area = 4πr²
= 4 x  (7) ² = 616 cm²

Case II:
r = 14 cm
Surface area = 4πr²
= 4 x \(\frac {22}{7}\) x (14)² = 2464 cm²
∴ Ratio of surface area of the balloon
= 616:2464 = \(\frac {616}{2464}\) = \(\frac {1}{4}\) = 1.4

Question 5.
A hemispherical bowl is made of brass has inner diameter 10.5 cm. Find the cost of tin-plating it on the inside at the rate of ₹ 16 per 100 cm².
Solution:
Inner diameter = 10.5 cm
∴ Inner radius (r) = \(\frac {10.5}{2}\) cm = 5.25 cm
∴ Inner surface area = 2πr²
= 2 x \(\frac {22}{7}\) x (5.25)²
= 173.25 cm²
∴ Cost of tin-plating at the rate of ₹ 16 per 100 cm²
= \(\frac {16}{100}\) x 173. 25
= ₹ 27.72

Question 6.
E Find the radius of a sphere whose surface area is 154 cm²
Solution:
Let the radius of the sphere be r cm.
Surface area = 154 cm²
4πr² = 154 = 4 x \(\frac {22}{7}\) x r² = 154
r² = \(\frac{154 \times 7}{4 \times 22}\)
r² = \(\frac {49}{4}\) = r = \(\sqrt{\frac{49}{4}}\)
∴ r= \(\frac {49}{4}\) = 3.5 cm
Hence, the radius of the sphere is 3.5 cm.

Question 7.
The diameter of the moon is approximately one fourth of the diameter of the earth. Find the ratio of their surface areas.
Solution:
Let the diameter of the earth be 2r.
Then diameter of the moon = \(\frac {1}{4}\) (2r) = \(\frac {r}{2}\)
∴ Radius of the earth = \(\frac {2r}{2}\) = r
and, radius of the moon = \(\frac {1}{2}\) = \(\frac {r}{2}\) = \(\frac {r}{4}\)
∴ Surface area of the earth = 4πr²
and, surface area of the moon
= 4ir \(\frac {r}{4}\)² = \(\frac {r}{4}\) πr²
∴ Ratio of their surface areas

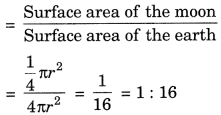
Question 8.
A hemispherical bowl is made of steel, 0.25 cm thick. The inner radius of the bowl is 5 cm. Find the outer curved surface area of the bowl.
Solution:
The inner radius of the bowl = 5 cm
Thickness of steel = 0.25 cm
∴ The outer radius of the bowl
= 5 + 0.25 = 5.25 cm
∴ The outer curved surface area of the bowl
4πr = 4 x \(\frac {22}{7}\) x (5.25)²
= 346.5 cm²

Question 9.
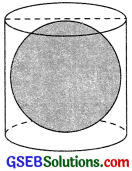
A right circular cylinder just encloses a sphere of radius r. Find
1. the surface area of the sphere,
2. the curved surface area of the cylinder,
3. the ratio of the areas obtained in (i) and (ii).

Solution:
1. The surface area of the sphere = 4πr²

2. For cylinder:
The radius of the base = r
Height = 2r
∴ The curved surface area of the cylinder
= 2π(r) (2r) = 4πr²

3. Ratio of the areas obtained in (i) and (ii)