Gujarat Board GSEB Textbook Solutions Class 9 Maths Chapter 15 Probability Ex 15.1 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 9 Maths Chapter 15 Probability Ex 15.1
Question 1.
In a cricket match, a batswoman hits a boundary 6 times out of 30 balls she plays. Find the probability that she did not hit a boundary.
Solution:
Let E be the event of hitting the boundary.
Then,
Number of times the batswoman
![]()
= \(\frac {6}{30}\) = \(\frac {1}{5}\)
Probability of not hitting the boundary
= 1 – probability of hitting the boundary
= 1 – P(E) = 1 – \(\frac {1}{5}\) = \(\frac {4}{5}\) or 0.8.
Question 2.
1500 families with 2 children were selected randomly, and the following data were recorded:

Compute the probability of a family, chosen at random, having
1. 2 girls
2. 1 girl
3. no girl
Also, check whether the sum of these probabilities is 1.
Solution:
Total number of families = 475 + 814 + 211 = 1500
1. Probability of a family, chosen at random having 2 girls
= \(\frac {475}{1500}\) = \(\frac {19}{60}\)
2. Probability of a family, chosen at random, having 1 girl
= \(\frac {814}{1500}\) = \(\frac {407}{750}\)
3. Probability of a family, chosen at random, having no girl
\(\frac {211}{1500}\)
Sum of these probabilities
= \(\frac{19}{60}+\frac{407}{750}+\frac{211}{1500}\)
= \(\frac{475+814+211}{1500}\)
= \(\frac {1500}{1500}\) = 1
Hence, the sum is checked.
![]()
Question 3.
In a particular section of class-IX, 40 students were asked about the months of their birth, the following graph was prepared for the data so obtained. Find the probability that a student of the class was born in August.
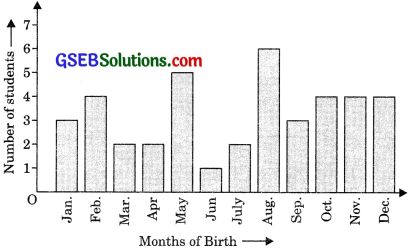
Solution:
A total number of students born in the year.
= 3 + 4 + 2 + 2 + 5 + 1 + 2 + 6 + 3 + 4 + 4 + 4 = 40
Number of students born in August = 6
∴ Probability that a student of the class was born in August
= \(\frac {6}{40}\) = \(\frac {3}{20}\)
Question 4
Three coins are tossed simultaneously 200 times with the following frequencies of different outcomes.
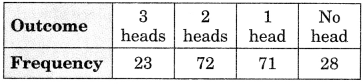
If the three coins are simultaneously tossed again, compute the probability of 2 heads coming up.
Solution:
The total number of times the three coins are tossed = 200.
A number of times when 2 heads appear = 72.
∴Probability of 2 heads coming up
= \(\frac {72}{200}\) = \(\frac {9}{25}\)
![]()
Question 5.
An organization selected 2400 families at random and surveyed them to determine a relationship between income level and the number of vehicles in a family. The information gathered is listed in the table below:
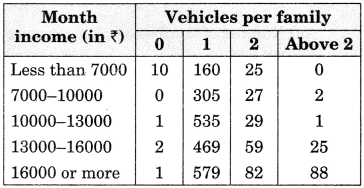
Suppose a family is chosen. Find the probability that the family has chosen is:
- earning ₹ 1000 ₹ 13000 per month and owning exactly 2 vehicles.
- earning ₹ 16000 or more per month and owning exactly 1 vehicle.
- earning less than ₹ 7000 per month and does not own any vehicle.
- earning ₹ 13000 ₹ 16000 per month and owning more than 2 vehicles.
- owning not more than 1 vehicle.
Solution:
Total number of families selected = 2400.
1. A number of families earning ₹ 10000 ₹ 13000 per month and owning exactly 2 vehicles = 29.
∴ probability that the family has chosen is earning ₹ 10000 ₹ 13000 per month and
owning exactly 2 vehicles = \(\frac {29}{2400}\)
2. A number of families earning ₹ 16000 or more per month and owning exactly 1 vehicle = 579.
∴ Probability that the family chosen is earning ₹ 16000 or more per month and
owning exactly 1 vehicle = \(\frac {579}{2400}\) = \(\frac {193}{800}\)
3. Number of families earning less than 7000 per month and does not own any vehicle in = 10
∴ Probability that the family chosen is earning less than ₹ 7000 per month and does not own any vehicle = \(\frac {10}{2400}\) = \(\frac {1}{240}\)
4. Number of families earning ₹ 13000 ₹ 16000 per month and owning more than 2 vehicles = 25.
∴ Probability that the family chosen is earning ₹ 13000-₹ 16000 per month and
owning more than 2 vehicles = \(\frac {25}{2400}\) = \(\frac {1}{96}\)
5. Number of families owning not more than 1 vehicle
= Number of families owning 0 vehicle + Number of families owning 1 vehicle
= (10 + 0 + 1 + 2 + 1) + (160 + 305 + 535 + 469 + 579) = 14 + 2048 = 2062
∴ Probability that the family chosen owns not more than 1 vehicle = \(\frac {2062}{2400}\) = \(\frac {1031}{1200}\)
![]()
Question 6.
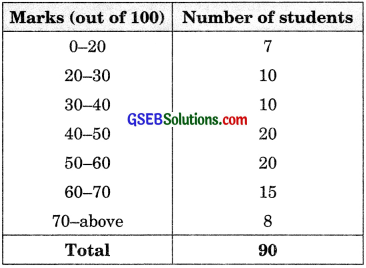
1. Find the probability that a student obtained less than 20% in the mathematics test.
2. Find the probability that a student obtained marks 60 or above.
Solution:
Total number of students = 90
1. Number of students obtaining less than
20% in the mathematics test = 7
∴ Probability that a student obtained less
than 20% in mathematics test = \(\frac {7}{90}\)
2. Number of students obtaining marks 60 or above= 15 + 8 = 23.
∴ Probability that a student obtained marks 60 or above = \(\frac {23}{90}\)
Question 7.
To know the opinion of the students about the subject statistics, a survey of 200 students was conducted. The data is recorded in the following table:

Find the probability that a student is chosen at random:
1. like statistics
2. does not like it.
Solution:
The total number of students = 200.
1. The number of students who like statistics = 135.
∴ Probability that a student chosen at
random likes statistics \(\frac {135}{200}\) = \(\frac {27}{40}\)
2. Number of students who do not like statistics = 65.
∴ Probability that a student chosen at random does not like it \(\frac {65}{200}\) = \(\frac {13}{40}\)
Aliter: Probability that a student chosen at random does like statistics = 1 – probability that a student chosen at random like statistics = 1 – \(\frac {27}{40}\) = \(\frac {13}{40}\)
![]()
Question 8.
The distance (in km) of 40 female engineers from their residence to their place of work was found as follows:

What is the empirical probability that an engineer lives:
- less than 7 km from her place of work?
- more than or equal to 7 km from her place of work?
- within km from her place of work?
Solution:
The total number of female engineers = 40.
1. A number of female engineers whose distance (in km) from their residence to their place of work is less than 7 km = 9.
∴ Probability that an engineer lives less than 7 km from her place of work = \(\frac {9}{40}\)
2. Number of female engineers whose distance (in km) from their residence to their place of work is more than or equal to 7 km = 31.
∴ Probability that an engineer lives more than or equal to 7 km from her place of residence =\(\frac {31}{40}\)
Aliter: Probability that an engineer lives more than or equal to 7 km from her place of residence
= 1 – probability that an engineer lives less than 7 km from her place of work.
= 1 – \(\frac {9}{40}\) = \(\frac {31}{40}\)
3. Number of female engineers whose distance (in km) from their residence to their place of work is within \(\frac {1}{2}\) km = 0.
∴ Probability that an engineer lives within
\(\frac {1}{2}\) km from her place of work = \(\frac {0}{40}\) = 0.
![]()
Question 9.
Activity: Note the frequency of two-wheelers, three-wheelers, and four-wheelers going past during a time interval, in front of your school gate. Find the probability that any one vehicle out of the total vehicles you have observed is a two-wheeler.
Solution:
Do it yourself.
Question 10.
Activity: Ask all the students in your class to write a 3-digit number. Choose any student from the room at random. What is the probability that the number written by her/him is divisible by 3? Remember that a number is divisible by 3, if the sum of its digits is divisible by 3.
Solution:
Do it yourself.
Question 11.
Eleven bags of wheat flour, each marked 5 kg actually contained the following weights of flour (in kg).
![]()
Find the probability that any of these bags chosen at random contains more than 5 kg of flour.
Solution:
A total number of bags of wheat flour =11.
No. of bags containing more than 5 kg of wheat flour = 7.
∴ Probability that any of these bags chosen at random contains more than 5 kg of flour = \(\frac {7}{11}\)
![]()
Question 12.
A study was conducted to find out the concentration of sulfur dioxide in the air in parts per million (ppm) of a certain city. The data obtained for 30 days is as follows:

Using the frequency distribution table, find the probability of the concentration of sulfur dioxide in the interval 0.12 — 0.16 on any of these days.
Solution:
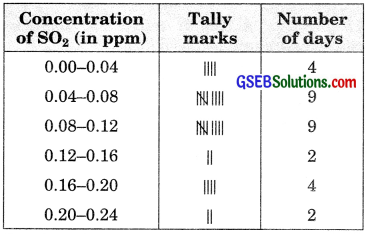
Total numbers of days = 30
No. of days for which the concentration of SO2
is in the interval 0.12-0.16 = 2.
⇒ Required probability = \(\frac {2}{30}\) = \(\frac {1}{15}\)
Question 13.
The blood groups of 30 students of class VIII are recorded as follows:
A, B, O, O, AB, O, A, O, B. A, O, B, A, O, O.
A, AB, O, A, A, O, O, AB, B, A, O, B, A, B, O.
Using this frequency distribution, determine the probability that a student of this class, selected at random, has blood group AB.
Solution:
Frequency distribution table.
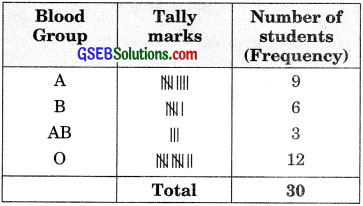
The total number of students = 30.
No. of students having blood group AB = 3.
∴ Required probability = \(\frac {3}{30}\) = \(\frac {1}{10}\)
![]()