Gujarat Board GSEB Solutions Class 9 Maths Chapter 6 Lines and Angles Ex 6.1 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 9 Maths Chapter 6 Lines and Angles Ex 6.1
Question 1.
In the given figure AB and CD intersect at O. If ∠AOC + ∠BOE = 70°, and ∠BOD = 40°, find ∠BOE and reflex ∠COE.
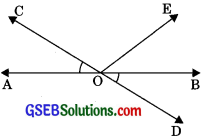
Solution:
It is given that
∠AOC +∠BOE = 70° ………..(1)
∠AOC = ∠BOD
⇒ ∠AOC = 40°
Putting in eqn. (1),
40° + ∠BOE = 70°
∠BOE = 70° – 40°
⇒ ∠BOE = 30°
∠AOE + ∠BOE = 180° (Linear pair)
∠AOC + ∠COE + ∠BOE = 180°
⇒ ∠AOC + ∠BOE + ∠COE = 1800
⇒ 70° +∠COE = 180°
⇒ ∠COE = 180° – 70°
⇒ ∠COE = 110°
Now, Reflex ∠COE = 360° – 110° = 250°
![]()
Question 2.
In figure lines XY and MN intersect at O. If ∠POY = 90°and a : b = 2 : 3, find c.
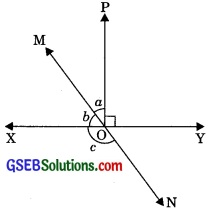
Solution:
Let a = 2 x and b = 3x
∠POX + ∠POY = 180° (Linear pair)
∠POX + 90° = 180°
∠POX = 180° – 90° = 90°
⇒ a + b = 90°
⇒ 2x + 3x = 90°
⇒ 5x = 90°
⇒ x = \(\frac {90°}{5}\) = 18°
∴ a = 2x = 2 x 18°= 36°
⇒ b = 3x = 3 x 18°= 54°
Now, ∠XON + ∠YON = 180° (Linear pair)
⇒ c + 54° = 180° (∠XOM = b and ∠XON = c)
⇒ c = 180° – 54°
⇒ c = 126°
![]()
Question 3.
In figure ∠PQR = ∠PRQ, then prove that ∠PQS = ∠PRT.
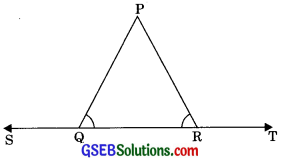
Solution:
Given: ∠PQR = ∠PRQ
To Prove: ∠PQS = ∠PRT
Proof: ∠PQS + ∠PQR = 180° ………. (1) (Linear pair)
∠PRQ +∠PRT = 180° ………(2) (Linear pair)
But ∠PQR =∠PRQ
Putting value ∠PQR from eqn. (3) in eqn. (1)
∠PQS + ∠PRQ = 180°
Now from eqn. (2) and (4), we have
∠PQS + ∠PRQ = ∠PRQ + ∠PRT
∠PQS = ∠PRT
Question 4.
In the given figure, if x + y = w + z, then prove that AOB is a line.
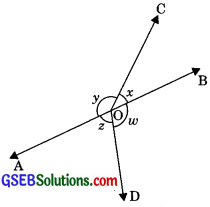
Solution:
Given: x + y = w + z
To Prove: AOB is a line.
Proof: ∠BOC + ∠AOC +∠BOD + ∠AOD = 360°
(Sum of all angles round a point is equal to 360°)
x + y + w + z = 360° ……..(1)
But x + y = w + z ……..(2)
From eqn. (1) and (2), we have
w + z + w + z = 360°
⇒ 2w + 2z = 360°
⇒2(w + z) = 360°
⇒ w + z = \(\frac{360°}{2}\)
⇒ w + z = 180°
w + z = 180° (Linear pair)
Hence,
∠BOD + ∠AOD = 180°
Therefore AOB is a line.
![]()
Question 5.
In figure, POQ is a line. Ray OR is perpendicular to line PQ. OS is another ray lying between ray OP and OR. Prove that
∠ROS = \(\frac{1}{2}\)(∠QOS – ∠POS).
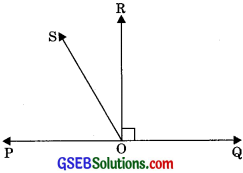
Solution:
Given: Ray OR ⊥ PQ and ray OS is another ray lying between OP and OR.
To Prove: ∠ROS = (∠QOS – ∠POS)
Proof: Ray OR ⊥ PQ
∴ ∠POR = ∠ROQ = 90°
Now, ∠POS = ∠POR – ∠ROS
∠POS = 90° – ∠ROS ………..(1)
∠QOS = ∠QOR + ∠ROS
∠QOS = 90° + ∠ROS ……..(2)
Subtracting eqn (2) from eqn (1),
∠QOS – ∠POS = 90° + ∠ROS – (90°- ∠ROS)
∠QOS – ∠POS = 90° + ∠ROS – 90° + ∠ROS
∠QOS – ∠POS = 2∠ROS
2 ∠ROS = ∠QOS – ∠POS
∠ROS = \(\frac{1}{2}\)(∠QOS – ∠POS)
![]()
Question 6.
It is given that ∠XYZ = 640 and XY is produced to point P. Draw a figure from the given information. If ray YQ bisects ∠ZYP, find ∠XYQ and reflex ∠QYP.
Solution:
∠XYZ = 64°
Ray YZ stands on PX.
∠XYZ + ∠PYZ = 180° (Linear pair)
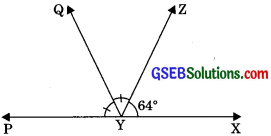
64° + ∠PYZ = 180°
⇒ ∠PYZ = 180°- 64°
⇒ ∠PYZ = 116°
⇒ ∠QYZ = \(\frac{∠PYZ}{2}\)
(YQ is the bisector of ∠PYZ)
∠QYZ = \(\frac{116°}{2}\)
∠QYZ = 58°
∠XYQ = ∠XYZ + ∠ZYQ = 64° + 58°
∠XYQ = 122°
∠QYP = ∠QYZ
(YQ is the bisector of ∠PYZ)
∠QYP = 58°
Reflex ∠QYP = 360° – 58°
Reflex ∠QYP = 302°
![]()