Gujarat Board GSEB Solutions Class 9 Maths Chapter 7 Triangles Ex 7.1 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 9 Maths Chapter 7 Triangles Ex 7.1
Question 1.
In quadrilateral ABCD, AC = AD, and AB bisect ∠A (see in figure). Show that ΔABC ≅ ΔABD. What can you say about BC and BD?
Solution:
Given: Quadrilateral ABCD in which AB is the bisector of ∠A and AC = AD.
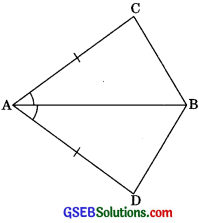
To show:
ΔABC ≅ ΔABD
Proof: In ΔABC and ΔABD,
AC = AD (Given)
∠BAC = ∠BAD
(AB is the bisector of ∠A)
AB = AB (Common)
∴ ΔABC ≅ ΔABD (by SAS Congruency)
Hence BC = BD (by CPCT)
c
Question 2.
ABCD is a quadrilateral in which AD = BC and
∠DAB = ∠CBA (see figure). Prove that
1. ΔABD ≅ ΔBAC
2. BD = AC
3. ∠ABD = ∠BAC
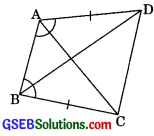
Solution:
Given: ABCD is a quadrilateral in which
AD = BC and ∠DAB = ∠CBA.
1. In ΔABD and ΔBAC,
AD = BC (given)
∠DAB = ∠CBA (given)
AB = AB (common)
∴ ΔABD ≅ ΔBAC (by SAS congruency)
2. ΔABD ≅ ΔBAC (proved above)
∴ BD = AC (byCPCT)
3. ΔABD ≅ ΔBAC (proved above)
∴ ∠ABD = ∠BAC (by CPCT)
![]()
Question 3.
AD and BC are equal perpendiculars to a line segment AB (see fig). Show that CD bisects AB.
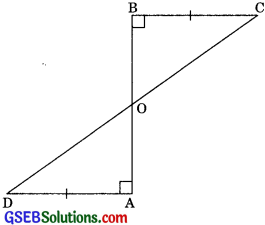
Solution:
Given: AD and BC are perpendiculars on AB
such that AD = BC.
To Prove: CD bisects AB.
i.e., OA = OD
Proof: In ΔAOD and ΔBOC,
AD = BC (Given)
∠OAD = ∠OBC (each 900)
AD || BC (If alternate interior angles are equal then lines are parallel)
∴ ∠ADO = ∠OCB (Alternate interior angle)
Hence ΔAOD ≅ ΔBOC (by ASA congruency)
Therefore, OA = OB (by CPCT)
∴ CD bisects AB.
![]()
Question 4.
l and m are two parallel lines intersected by another pair of parallel lines p and q (see in figure). Show that
ΔABC ≅ ΔCDA
Solution:
Given: l || m and both are intersected by another pair of parallel lines p and q
To Prove: ΔABC ≅ ΔCDA
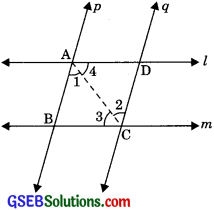
Proof: Since AB || CD
and AD||BC
Now in ΔABC and ΔADC,
∠1 = ∠2 (Alternate interior angles
∠3 = ∠4 (Alternate interior angles)
and AC = AC (common)
ΔABC ≅ ΔADC (by ASA congruency)
Question 5.
Line l is the bisector of an angle ∠A and B is any point on l. BP and BQ are perpendiculars from B to the arms of ∠A (see figure). Show that
(i) ΔAPB ≅ ΔAQB
(ii) BP = BQ or B is equidistant from the arms of ∠A.
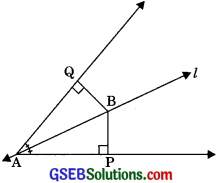
Solution:
Given: l is the bisector of ∠A, i.e., ∠BAP = ∠BAQ.
BP and BQ are perpendiculars from B to arms of ∠A.
(i) In ΔAPB and ΔAQB
∠BPA = ∠BQA (each 90°)
∠BAP = ∠BAQ (l is the angle bisector of ∠A)
and AB = AB (Common)
Hence ΔAPB ≅ ΔAQB (By AAS congruency)
(ii) Since ΔAPB ≅ ΔAQB
∴ BP = BP (By CPCT)
![]()
Question 6.
In figure,AC = AE, AB = AD and ∠BAD = ∠EAC. Show that BC = DE.
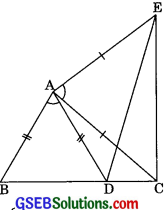
Solution:
Given: In figure AC = AE.
and AB = AD
and ∠BAD = ∠EAC
To show: BC = DE
Proof: In ΔABC and ΔADE,
AB = AD (given)
∠BAD = ∠EAC (given)
Adding ∠DAC on both sides, we get
∠BAD + ∠DAC = ∠EAC + ∠DAC
⇒ ∠BAC = ∠DAE
AC = AE (given)
∴ ΔBAC ≅ ΔDAE (By SAS congruency)
Hence BC = DE (By CPCT)
![]()
Question 7.
AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that ∠BAD = ∠ABE and ∠EPA = ∠DPB (see figure). Show that.
(i) ADAP AEBP
(ii) AD = BE
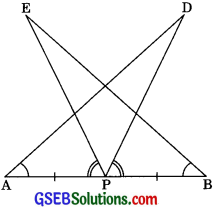
Solution:
Proof: (i) In ΔDAP and ΔEBP,
∠BAD = ∠ABE (given)
or ∠DAP = ∠PBE
AP = PB (P is the mid≅points)
∠EPA = ∠DPB (given)
Adding ∠DPE on both sides, we get
∠EPA + ∠DPE = ∠DPB + ∠DPE
∠DPA = ∠EPB
∴ ΔDAP ≅ ΔEBP (By ASA congruency)
(ii) ΔDAP ≅ ΔEBP
∴ AD = BE (by CPCT)
Question 8.
In right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see figure). Show that:
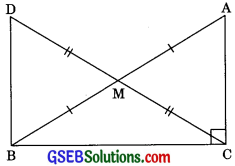
1. ∠AMC ≅ ΔBMD
2. ∠DBC is a right angle.
3. ΔDBC ≅ ΔACB
4. CM = \(\frac {1}{2}\)AB
Solution:
Proof:
1. In ΔAMC and ΔBMD,
AM = BM (M is the mid-point of AB)
∠AMC = ∠BMD (Vertically opposite angle)
CM = DM (given)
Hence, ΔAMC ≅ ΔBMD (by SAS congruency)
AC = BD (by CPCT)
![]()
2. ΔAMC ≅ ΔBMD (Proved in part i)
∴ ∠ACM = ∠BDM (by CPCT)
(Alternate interior angles)
Hence AC || BD (If alternate interior angles are equal then lines are parallel)
∴ ∠ACB + ∠DBC = 180°
(Sum of consecutive interior angles is equal to 180°
∴ ∠DBC = 180°≅ 90°
⇒ ∠DBC = 90°
Hence ∠DBC is a right angle.
3. Now in ΔACB and ΔDBC,
∠ACB = ∠DBC (each 900)
BC = CB (common)
AC = BD (Proved in part i)
Hence ΔACB ≅ ΔDBC (by SAS congruency)
4. ΔDBC ≅ ΔACB (Proved in part iii)
DC = AB (by CPCT)
⇒ 2CM = AB (DM = CM)
CM = \(\frac {1}{2}\) AB