Gujarat Board GSEB Solutions Class 9 Maths Chapter 7 Triangles Ex 7.2 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 9 Maths Chapter 7 Triangles Ex 7.2
Question 1.
In an isosceles triangle ABC, with AB = AC, the bisectors of ∠B and ∠C intersect each other at O. Join A to O. Show that.
1. OB = OC
2. AO bisects ∠A
Solution:
1. AB = AC (given)
∠B = ∠C
(Angle opposite to equal sides are equal)
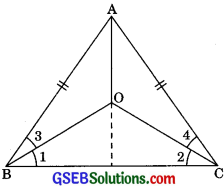
∠B = ∠C (Dividing by 2)
(OB and OC angle bisectors of ∠B and ∠C)
⇒ ∠1 = ∠2
Hence OB = OC
(Sides opposite to equal angles are equal)
2. Now in ΔAOB and ΔAOC
AB = AC (given)
∠B = ∠C (Angle opposite to equal sides are equal)
⇒\(\frac {1}{2}\)∠B = \(\frac {1}{2}\)∠C (Dividing by 2)
⇒∠3 = ∠4
and OB = OC (Proved above)
Hence ∠AOB ≅ ∠AOC (by SAS congruency)
∴ ∠OAB = ∠OAC (By CPCT)
Hence AO bisects ∠A.
![]()
Question 2.
In ΔABC, AD is the perpendicular bisector of BC (see in figure). Show that ΔABC is an isosceles triangle in which AB = AC.
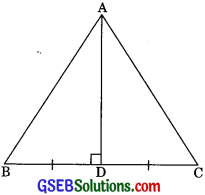
Solution:
Given: ΔABC in which AD ⊥ BC
and BD = CD
To Prove: ΔABC is an isosceles triangle in which
AB = AC
Proof: In ΔADB and ΔADC,
BD = CD (AD is lar bisector of BC)
∠ADB = ∠ADC (each 90°)
AD = AD (Common)
∴ ΔADB ≅ ΔADC (By SAS congruency)
∴ AB = AC (by CPCT)
Therefore ABC is an isosceles triangle in which AB = AC.
Question 3.
ABC is an isosceles triangle in which altitudes BF and CF are drawn to equal sides AC and AB respectively (See figure). Show that these altitudes are equal.
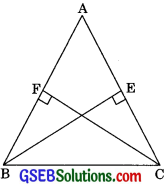
Solution:
Given: ABC is an isosceles triangle in which BE and CF are altitudes on AC and AB respectively.
To Prove:
BE = CF
Proof: In ΔABE and ΔACF,
AB = AC (Equal sides of an isosceles triangle)
∠AEB = ∠AFC (each 90°)
∠BAE = ∠CAF (Common)
∴ ΔAEB ≅ ΔACF (By AAS congruency)
Hence BE = CF (by CPCT)
![]()
Question 4.
ABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see figure). Show that
(i) ΔABE ≅ ΔACF
(ii) AB = AC (i.e. ABC is an isosceles triangle
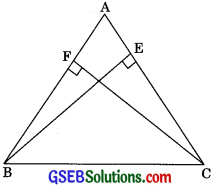
Solution:
Given: ΔABC in which BE = CF.
(i) In ΔABE and ΔACF,
∠BAE = ∠CAF (Common)
∠AEB = ∠AFC (Each 900)
BE = CF (given)
∴ ΔABE ≅ ΔACF (By AAS congruency)
(ii) ΔABE ≅ ΔACF (Proved above in part i)
∴ AB = AC (by CPCT)
ΔABC is an isosceles triangle.
Question 5.
ABC and DBC are two isosceles triangles on the same base BC (see figure). Show that ∠ABD = ∠ACD.
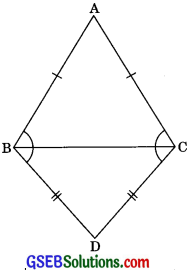
Solution:
ABC is an isosceles triangle.
AB = AC (given)
∠ABC = ∠ACB ……..(1) (Angles opposite to equal sides are equal)
Now DBC is an isosceles triangle.
BD = CD (given)
∴ ∠DBC = ∠DCB (Angles opposite to equal sides are equal)
Adding equation (1) and (2), we get
∠ABC + ∠DBC = ∠ACB + ∠DCB
∠ABD = ∠ACD
![]()
Question 6.
ΔABC is an isosceles triangle in which AB = AC. Side BA is produced to D such that AD = AB. (see figure). Show that ∠BCD is a right angle.
Or
In the given figure AB = AC and AB = AD, Prove that ∠BCD = 90°.
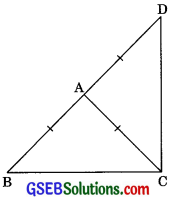
Solution:
ΔABC is an isosceles triangle.
AB = AC (given)
∴ ∠ABC = ∠ACB
(Angles opposite to equal sides are equal)
In ΔACD,
AB = AD (by construction)
But AB = AC
∴ AD = AC
∠ADC = ∠ACD …….(2)
(Angles opposite to equal sides are equal)
Adding eqn. (1) and (2), we get
∠ABC + ∠ADC = ∠ACB + ∠ACD
∠ABC + ∠ADC = ∠BCD
∠ABC + ∠BDC = ∠BCD ………(3)
(∠ADC = ∠BDC)
Now in ∠ABC,
∠ABC + ∠BDC + ∠BCD = 180° (By Angle Sum Property)
∠BCD + ∠BCD = 180°
[From eqn. (3)]
2 ∠BCD = 180°
∠BCD = \(\frac {180°}{2}\)
∠BCD = 90°
![]()
Question 7.
ABC is a right-angled triangle in which ∠A = 90°, and AB = AC. Find ∠B and ∠C.
Solution:
In ΔABC,
AB = AC
∠B = ∠C
(Angles opposite to equal sides are equal)
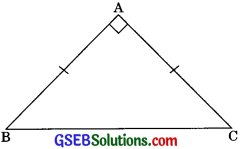
Now in ∠ABC,
∠A + ∠B + ∠C = 180° (by angle sum property)
90°+ ∠C + ∠C = 180° (∠B = ∠C)
2∠C = 180° – 90°
2∠C = 90°
∠C = 45°
∠B = ∠C = 45°
Question 8.
Show that the angles of an equilateral triangle are 60° each.
Solution:
Given: ABC is an equilateral triangle.
To Show:
∠A = ∠B = ∠C = 60°
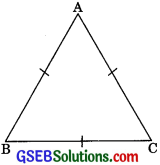
Proof: ABC is an equilateral triangle.
∴ AB = AC
∴ ∠C = ∠B …….(1) (Angles opposite to equal sides are equal)
BC = AC
∠A = ∠B ………(2) (Angles opposite to equal sides are equal)
From eqn. (1) and (2), we get
∠A = ∠B = ∠C = x (Say)
Now in ΔABC,
∠A + ∠B + ∠C = 180°
x + x + x = 180°
3x = 180°
x = 60°
Hence ∠A + ∠B = ∠C = 60°
![]()