GSEB Solutions Class 11 Maths Chapter 2 Relations and Functions Ex 2.2

Gujarat Board GSEB Textbook Solutions Class 11 Maths Chapter 2 Relations and Functions Ex 2.2 Textbook Questions and Answers.

Gujarat Board Textbook Solutions Class 11 Maths Chapter 2 Relations and Functions Ex 2.2

Question 1.
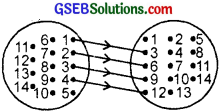
Let A = {1, 2, 3, ………………. 14}. Define a relation R from A to A by R = {(x, y) : 3x – y = 0, where x, y ∈ A}. Write down its domain, co-domain and range?
Solution:
(i) R = {(x, y) : 3x – y = 0, where x, y ∈A}
= {(1, 3), (2, 6), (3, 9), (4, 12)}
(ii) Domain : {1, 2, 3, …, 14}
(iii) Co-domain : {1, 2, 3, …, 14}
(iv) Range : {3, 6, 9, 12}

Question 2.
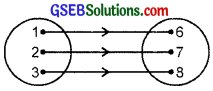
Define a relation R on the set N of natural numbers by R = {x, y) : y = x + 5, x is a natural number less than 4; x, y ∈ N}. Depict this relationship using (i) roster form (ii) an arrow diagram. Write down the domain and range?
Solution:
(i) R = {(x, y) : x = y – 5, x is a natural number less than 4; x, y ∈ N}
(ii) R = {(1,6), (2, 7), (3, 8)}
(iii) Domain = {1, 2, 3}
Range = {6, 7, 8}

Question 3.
A = {1, 2, 3, 5} and B = {4, 6, 9}. Define a relation R from A to B by R = {(x, y) : the difference between x and y is odd, x ∈ A, y ∈ B}. Write R in roster form?
Solution:
R = {(x, y) : the difference between x and y is odd, x ∈ A, y ∈ B},
where A – {1, 2, 3, 5} and B = {4, 6, 9).
Here, R = {(1, 4), (1, 6), (2, 9), (3, 4), (3, 6), (5, 4), (5, 6)}

Question 4.
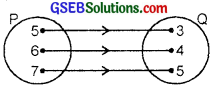
Figure given below shows a relationship between the sets P and Q. Write this relation
(i) in set builder form
(ii) roster form. What is its domain and range?

Solution:
(i) R = {(x, y) : x – y = 2, 4 < x < 8, x, y ∈ N}
(ii) R = {(5, 3), (6, 4), (7, 5)}
Domain = (5, 6, 7}, Range = (3, 4, 5}.

Question 5.
Let A = {1, 2, 3, 4, 6}. Let R be the relation on A defined by {(a, b) : a ∈ A, A ∈ a divides 6}.

1. Write R in roster form.
2. Find the domain of R.
3. Find the range of R.

Solution:

1. Given A = {1, 2, 3, 4, 6} and R is the relation on A defined by {(a, b): a ∈ A, b ∈ A, a divides b)
   Clearly, R = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 6), (2, 2), (2, 4), (2, 6), (3, 3), (3, 6), (4, 4), (6, 6)}.
2. Domain (R) = {1, 2, 3, 4, 6}
3. Range (R) = {1, 2, 3, 4, 6).

Question 6.
Determine the domain and the range of the relation R defined by R = {x, x + 5) : x ∈ (0, 1, 2, 3, 4, 5}}
Solution:
Here, R = {(x, x + 5) : x ∈ (0, 1, 2, 3, 4, 5)
∴ Domain (R) = {(0, 1, 2, 3, 4, 5, 6)}
[On putting x = 0, 1, 2, 3, 4, 5 in x]
and Range (R) = (5, 6, 7, 8, 9, 10)
[On putting x = 0, 1, 2, 3, 4, 5 in x + 5]

Question 7.
Write the relation R = {(x, x³) : x is a prime number less than 10} in roster form?
Solution:
Prime numbers less than 10 are 2, 3, 5, 7.
R = {(2, 8), (3, 27), (5, 125), (7, 343)}.

Question 8.
Let A as {x, y, z} and B = {1, 2}. Find the number of relations from A into B?
Solution:
A = {x, y, z) and B = {1, 2}.
A × B = {(x, 1), (x, 2), (y, 1), (y, 2), (2,1), (2, 2)}
Now n(A × B) = 6.
Therefore, the number of subsets of n(A × B) is 26 = 64.
So, the number of relations from A into B is 64.

Question 9.
Let R be the relation on Z defined by R = {(a, b) : ∈ Z, a – b is an integer}. Find the domain and range of R?
Solution:
R = {(a, b) : a ∈ Z, b ∈ Z, a – b is an integer}
= {(a, b) : a ∈ Z, b ∈ Z, a and b both are integers}.
Domain (R) = Z.
Range (R) = Z.