Gujarat Board GSEB Textbook Solutions Class 11 Maths Chapter 5 Complex Numbers and Quadratic Equations Ex 5.2 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 11 Maths Chapter 5 Complex Numbers and Quadratic Equations Ex 5.2
Find the modulus and the argument of each of the complex numbers in questions 1 to 2:
1. z = – 1 – i\(\sqrt{3}\)
2. z = – \(\sqrt{3}\) + i
Solutions to questions 1 to 2:
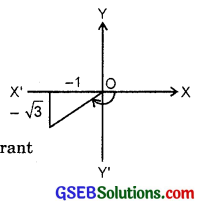
1. z = – 1 – i\(\sqrt{3}\)
∴ Let – 1 – i\(\sqrt{3}\) = r(cos θ + isinθ)
∴ – 1 = rcos θ and \(\sqrt{-3}\) = r sin θ
Squaring and adding, we get
4 = 1 + 3 = r2(cos2 θ + sin2 θ) = r2
∴ r = \(\sqrt{4}\) = 2
tan θ = \(\frac{\sqrt{3}}{-1}\) = – \(\sqrt{3}\).
where θ lies in third quadrant.
∴ θ = – 180° + 60° = – 120° = – \(\frac{2π}{3}\)
|z| = 2, arg z = – \(\frac{2π}{3}\)
2. z = – \(\sqrt{3}\) + i = r(cos θ + 180°)
∴ rcos θ = – \(\sqrt{3}\), r sin θ = 1
Squaring and adding (\(\sqrt{3}\))2 + 1 = 4
∴ r = 2, we get
tan θ = \(\frac{-1}{\sqrt{3}}\) ⇒ θ lies in II Quadrant
∴ θ = 180° – 30° = 150° = \(\frac{5π}{6}\)
∴ |z| = 2, arg z = \(\frac{5π}{6}\).
![]()
Convert each of the complex numbers given in questions 3 to 8 in the polar form:
3. 1 – i
4. – 1 + i
5. – 1 – i
6. – 3
7. \(\sqrt{3}\) + i
8. i
Solutions to questions 3 to 8:
3. If 1 – i = r(cos θ + isin θ)
∴ rcos θ = 1, rsin θ = – 1
Squaring and adding, we get
12 + 12 = r2
∴ r = \(\sqrt{2}\)
and tan θ = \(\frac{- 1}{1}\) = – 1.
∴ θ lies in IV quadrant, since sin θ is negative and cos θ is positive.
∴ θ = – 45° = – \(\frac{π}{4}\).
∴ Polar form of 1 – i is
\(\sqrt{2}\)[cos (- \(\frac{π}{4}\)) + isin (- \(\frac{π}{4}\))]
![]()
4. z = – 1 + i = r(cos θ + isin θ)
∴ rcos θ = – 1, r sin θ = 1
Squaring and adding, we get
r2 = (- 1)2 + 12 = 2 is r = \(\sqrt{2}\).
Here, sin θ is +ve and cos θ is – ve. Therefore, θ lies in the second quadrant.
i.e; θ = π – \(\frac{π}{4}\) = \(\frac{3π}{4}\).
∴ z = \(\sqrt{2}\)(cos \(\frac{3π}{4}\) + isin \(\frac{3π}{4}\)).
5. z = – 3 = r(cos θ + i sin θ)
∴ rcos θ = – 1, r sin θ = – 1
Squaring and adding, we get
r2 = (- 1)2 + (- 1)2 = z
∴ r = \(\sqrt{2}\).
6. z = – 3 = r(cos θ + i sin θ)
∴ rcos θ = – 3, rsin θ = 0.
Squaring and adding, we get r2 = (- 3)2
∴ r = 3.
tan θ = 0 ⇒ θ = π [∵ cos π = 0]
∴ – 3 = 3(cos π + isin π).
![]()
7. r = \(\sqrt{3}\) + i = r(cos π + isinπ)
∴ rcos θ = \(\sqrt{3}\), r sin θ = 1
Squaring and adding, we get
r2 = 3 + 1 = 4, r = 2.
Also, tan θ = \(\frac{1}{\sqrt{3}}\). Also, sin θ and cos θ both are positive.
∴ θ = 30° = \(\frac{π}{6}\).
Polar form of z is 2(cos \(\frac{π}{6}\) + isin \(\frac{π}{6}\)).
8. z = i = r(cos θ + isin θ)
∴ rcos θ = 0, r.sin θ = 1.
Squaring and adding, we get r2 = 1.
∴ r = 1.
Now, sin θ = 1, cos θ = 0 at θ = \(\frac{π}{2}\).
∴ Polar form of z is cos \(\frac{π}{2}\) + isin \(\frac{π}{2}\).