GSEB Solutions Class 11 Maths Chapter 15 Statistics Ex 15.3

Gujarat Board GSEB Textbook Solutions Class 11 Maths Chapter 15 Statistics Ex 15.3 Textbook Questions and Answers.

Gujarat Board Textbook Solutions Class 11 Maths Chapter 15 Statistics Ex 15.3

Question 1.
From the data given below, state which group is more variable A or B?

Solution:

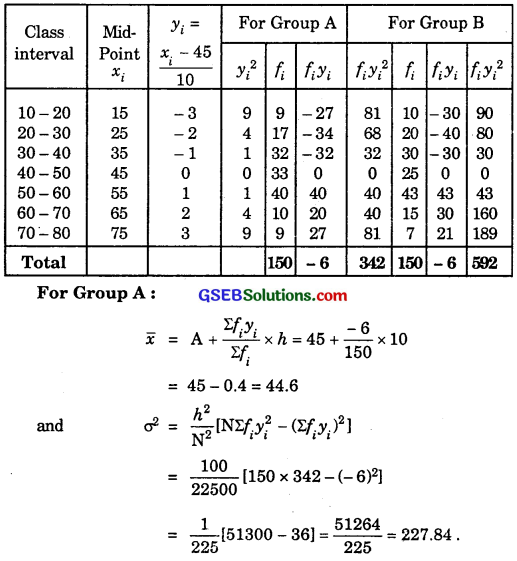
∴ σ = 15.09.
Coefficient of variance (C.V.)

For Gropu B:

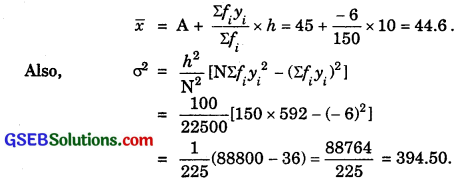
∴ σ = 19.86
Coefficient of variance (C.V.)
= \(\frac{σ}{x}\) × 100 = \(\frac{19.86}{44.6}\) × 100 = 44.53.
Coefficient of variation in group B is greater than the coefficient of variation in group A. Therefore, group B is more variable than group A.

Question 2.
From the prices of shares X and Y below, find out which is more stable in value:

Solution:

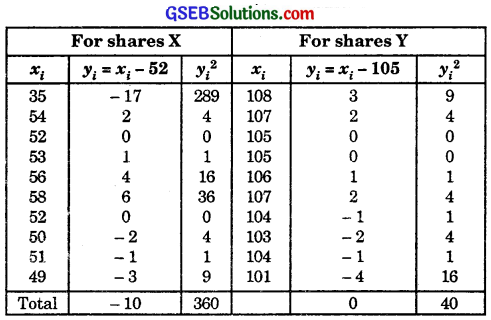
For shares X:

For shares Y:

Coefficient of variation in shares Y is less than the coefficient of variation in shares X.
Therefore, the share Y is more stable than the share X.

Question 3.
An analysis of monthly wages paid to workers in two firms A and B belonging to the same industry, give the following results:

(i) Which firm A or B pays out larger amount of monthly wages?
(ii) Which firm A or B, shows greater variability in individual wages?
Solution:
For firm A:
No. of wage earners = 586.
Mean of monthly wages \(\bar {x}\) = ₹ 5253.
Amount paid by firm A = ₹ (586 × 5253)
= ₹ 3078258.
Variance of distribution of wages = 100.
∴ Standard deviation = σ = \(\sqrt{Variance}\) = \(\sqrt{100}\)
= 10.
∴ Coefficient of variation = \(\frac{σ}{x}\) × 100
= \(\frac{10}{5253}\) × 100 = 0.19.

For firm B:
Number of wage earners = 648.
Mean of monthly wages \(\bar {x}\) = ₹ 5253.
Amount paid by firm B = ₹ 648 × 5253.
= ₹ 3403944.
∴ S.D. = σ = \(\sqrt{Variance}\) = \(\sqrt{121}\)
= 11.
∴ Coefficient of variation = \(\frac{σ}{x}\) × 100
= \(\frac{11}{5253}\) × 100 = 0.21
Monthly wages paid by firm A = ₹ 3078258.
Monthly wages paid by firm B = ₹ 3403944.
Firm B pays out larger amount as monthly wages.
Coefficient of vanation of wages of firm A = 0.19.
Coefficient of vanation of wages of firm B = 0.21.
Therefore, firm B shows greater variability in individual wages.

Question 4.
The following is the record of goals scored by team A in a football session:

For the team B, mean number of goals scored per match was 2 with standard deviation 1.25 goals. Find which team may be considered more consistent?
Solution:

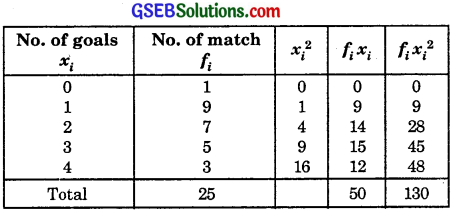
For Team A:

∴ Coefficient of variation
= \(\frac{σ}{x}\) × 100 = \(\frac{1.095}{2}\) × 100
= 54.75

For Team B:
Mean \(\bar {x} \) = 2
and S.D. = σ = 1.25.
Coefficient of variation
= \(\frac{σ}{x}\) × 100 = \(\frac{1.25}{2}\) × 100
= 62.5.
Coefficient of variation of goals of team A is less than that of B. Therefore, team A is more consistent than team B.

Question 5.
The sum and sum of squares corresponding to length x (in cm) and weight y (in grams) of 50 plant products are given below:
\(\sum_{i=1}^{50}\)x_i = 212, \(\sum_{i=1}^{50}\)x_i² = 902.8, \(\sum_{i=1}^{50}\)y_i = 261, \(\sum_{i=1}^{50}\)y_i² = 1457.6.
Which is more varying, the length or weight?
Solution:
For Length:

Coefficient of variation
= \(\frac{σ}{x}\) × 100 = \(\frac{0.28}{4.24}\) × 100 = 6.6

For weight:

Coefficient of variation of weight is more than that of length.
∴ Weight is more varying than length.