GSEB Solutions Class 11 Maths Chapter 15 Statistics Miscellaneous Exercise

Gujarat Board GSEB Textbook Solutions Class 11 Maths Chapter 15 Statistics Miscellaneous Exercise Textbook Questions and Answers.

Gujarat Board Textbook Solutions Class 11 Maths Chapter 15 Statistics Miscellaneous Exercise

Question 1.
The mean and variance of 8 observations are 9 and 9.25, respectively. If six of the observations are 6, 7, 10, 12, 12 and 13, find the remaining two observations.
Solution:
Let the remaining two observations be x and y. Then,

⇒ 74 = 210 + x² + y² – 216
⇒ 74 + 216 – 210 = x² + y² i.e., x² + y² = 80
or (x + y)² – 2xy = x² + y² = 80
i.e; 12² – 2xy = 80
⇒ – 2xy = 80 – 144
⇒ – 2xy = – 64
So, (x – y)² = x² + y² – 2xy
= 80 – 64 = 16
⇒ x – y = ± 4.
On solving equations x + y = 12 and x – y = ± 4, we get

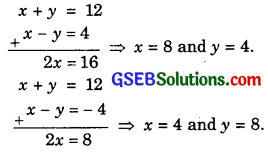
Thus, the remaining terms are 4 and 8.

Question 2.
The mean and variance of 7 observations are 8 and 16, respectively. If five of the observations are 2, 4, 10, 12 and 14, find the remaining two observations.
Solution:
Let the required remaining observations be x and y. Then,

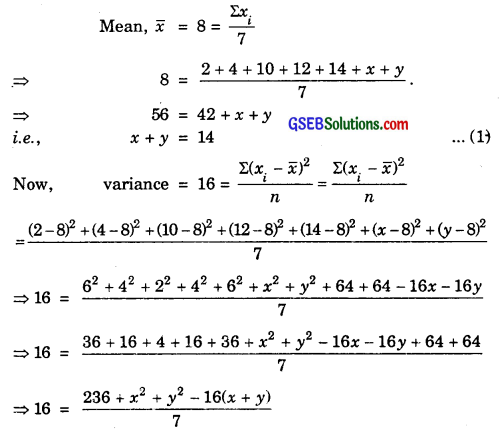
⇒ 112 = 236 + x² + y² – 16 × 4
⇒ 112 = x² + y² + 236 – 224
⇒ x² + y² = 100
i.e; (x + y)² = x² + y² + 2xy
⇒ 14² = 100 + 2xy
i.e; 196 – 100 = 2xy
⇒ 2xy = 96
So, (x – y)² = x² + y² – 2xy
= 100 – 96 = 4
i.e; x – y = ±2 ……………………. (2)
Solving (1) and (2) we get

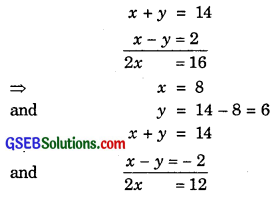
⇒ x = 6 and y = 8.
So, x = 6 and y = 8.
i.e; 6 and 8 are the remaining observations.

Question 3.
The mean and standard deviation of 6 observations are 8 and 4, respectively. If each observation is multiplied by 3, find the new mean and new standard deviation of the resulting observations.
Solution:
Let the observations be x₁, x₂, x₃, x₄, x₅ and x₆. So,

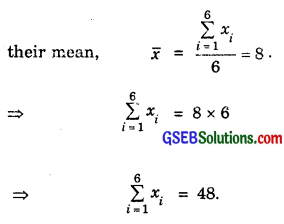
On multiplying each observation by 3, we get the new observations as 3x₁, 3x₂, 3x₃, 3x₄, 3x₅ and 3x₆. Now, their mean

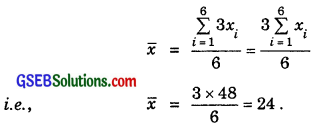
Variance of new observations

= \(\frac{9}{1}\) × Variance of old observations
= 9 × 4²
= 144.
∴ Standard deviation of new observations
= \(\sqrt{Variance}\) = \(\sqrt{144}\) = 12.

Question 4.
Given that \(\bar {x} \) is the mean and σ² is the variance of n observations x₁, x₂, x₃, ……………., x_n. Prove that the mean and variance of the observations ax₁, ax₂, ………….. ax_n are a\(\bar {x} \) and a²σ² respectively (a ≠ 0).
Solution:

Question 5.
The mean and standard deviation of 20 observations are found to be 10 and 2 respectively. On rechecking, it was found that an observation was incorrect. Caluculate the correct mean and standard deviation in each of the following cases:
(i) If the wrong item is omitted.
(ii) If it is replaced by 12.
Solution:

(i) Since the wrong item which has been omitted, the correct mean \(\frac{\sum_{i=1}^{20} x_{i}-8}{19}\), because on omitting the wrong item, the total number of observations left are 19.

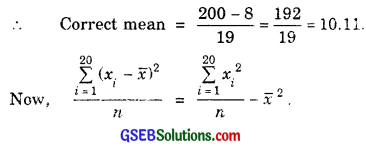
Since incorrect mean and variance are given as 10 and 4 respectively, so

= 106.105 – 102.212
= 3.893.
Correct S.D. = \(\sqrt{3.893}\) = 1.97

(ii) The wrong item which was 8 had been replaced by 12. As such, the correct mean
=
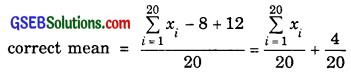
= \(\frac{200}{20}\) + \(\frac{1}{5}\)
= 10 + 0.2 = 10.2.
Since incorrect mean and variance are given as 10 and 4 respectively, so

Question 6.
The mean and standard deviation of marks obtained by 50 students of a class in the three subjects Mathematics, Physics and Chemistry are given below:

Which of the three subjects shows the highest variablility in marks and which shows the least?
Solution:
Subject Mathematics
Mean \(\bar {x} \) = 42, standard deviation σ = 12.
∴ Coefficient of variance = \(\frac{σ}{x}\) × 100
= \(\frac{12}{42}\) × 100 = 28.56.
Mean \(\bar {x} \) = 32, standard deviation σ = 15.
∴ Coefficient of variation = \(\frac{σ}{x}\) × 100
\(\frac{15}{32}\) × 100
= 46.875.
Subject chemistry
Mean \(\bar {x} \) = 40.9, standard deviation σ = 20.
∴ Coefficient of variation = \(\frac{σ}{x}\) × 100
= \(\frac{20}{40.9}\) × 100 = 48.9.
Highest variability of marks is in Chemistry and it is least in Mathematics.

Question 7.
The mean and standard deviation of a group of 100 observations were found to be 20 and 3 respecitvely. Later on it was found that three observations were incorrect, which were recorded as 21, 21 and 18. Find the mean and standard deviation, if the incorrect observations were omitted.
Solution:
Mean \(\bar {x} \) = \(\frac{\Sigma x_{i}}{n}\), \(\bar {x} \) = 20
∴ Σx_i = n × \(\bar {x} \) = 100 × 20 = 2000.
∴ Incorrect value of Σx_i = 2000.
∴ Correct value of Σx_i = 2000 – 21 – 21 – 18 = 1940
Correct value of mean = \(\frac{1940}{97}\) = 20.

Incorrect value of Σx_i² = 40900.
Correct value of Σx_i² = 40900 – (21)² – (21)² – (18)²
= 40900 – 441 – 441 – 324
= 39694
∴ Corrected σ² = \(\frac{39694}{97}\) – (20)²
= 409.22 – 400 = 9.22.
Correct value of standard deviation
σ = \(\sqrt{9.22}\) = 3.04.
Thus, corrected mean = 20
and correct value of σ = 3.04.