GSEB Solutions Class 12 Maths Chapter 7 Integrals Ex 7.10

Gujarat Board GSEB Textbook Solutions Class 12 Maths Chapter 7 Integrals Ex 7.10 Textbook Questions and Answers.

Gujarat Board Textbook Solutions Class 11 Maths Chapter 7 Integrals Ex 7.10

Evaluate the following integrals:
Question 1.
$\int_{0}^{1}$ $\frac{x}{x^{2}+1}$ dx
Solution:
Let I = $\int_{0}^{1}$ $\frac{x}{x^{2}+1}$ dx.
Put x² + 1 = t, 2x dx = dt.
When x = 1, t = 2 and when x = 0, t = 1.
∴ I = $\int_{2}^{1}$ $\frac{dt}{t}$

= log 2.

Question 2.
$\int_{0}^{\frac{\pi}{2}}$ $\sqrt{sinϕ}$cos⁵ϕdϕ
Solution:
Let I = $\int_{0}^{\frac{\pi}{2}}$ $\sqrt{sinϕ}$cos⁵ϕdϕ
= $\int_{0}^{\frac{\pi}{2}}$ $\sqrt{sinϕ}$cos⁴ϕcosϕdϕ
Put sinϕ = t so that cosϕ dϕ = dt.
When ϕ = 0, t = 0 and when ϕ = $\frac{π}{2}$, t = 1.

Question 3.
$\int_{0}^{1}$ sin^-1($\frac{2 x}{1+x^{2}}$)dx
Solution:

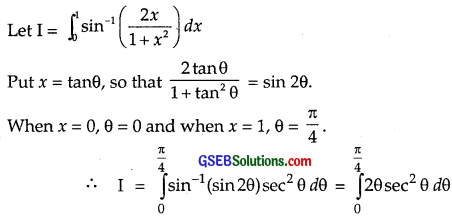
Integrating by parts, taking θ as first function,

Question 4.
$\int_{0}^{2}$x$\sqrt{x+2}$ dx
Solution:
Let I = $\int_{0}^{2}$x$\sqrt{x+2}$ dx
Put x + 2 = t² so that dx = 2t dt.
When x = 0, t = $\sqrt{2}$ and when x = 2, t² = 4 ⇒ t = 2.

Question 5.
$\int_{0}^{\frac{\pi}{2}}$ $\frac{\sin x}{1+\cos ^{2} x}$ dx
Solution:
Let I = $\int_{0}^{\frac{\pi}{2}}$ $\frac{\sin x}{1+\cos ^{2} x}$ dx
Put cos x = t so that – sin x dx = dt.
When x = 0, t = cos 0 = 1 and when x = $\frac{π}{2}$, t = cos $\frac{π}{2}$ = 0.

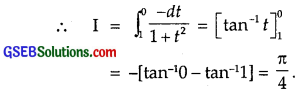
Question 6.
$\int_{0}^{2}$ $\frac{d x}{x+4-x^{2}}$
Solution:

Question 7.
$\int_{-1}^{1}$ $\frac{d x}{x^{2}+2 x+5}$
Solution:
Let

Question 8.
$\int_{1}^{2}$ ($\frac{1}{x}$ – $\frac{1}{2 x^{2}}$ e^2x dx
Solution:

Choose the correct answers in questions 9 and 10:
Question 9.
The value of the integral $\int_{\frac{1}{3}}^{1} \frac{\left(x-x^{3}\right)^{\frac{1}{3}}}{x^{4}}$ dx is
(A) 6
(B) 0
(C) 3
(4) 4
Solution:

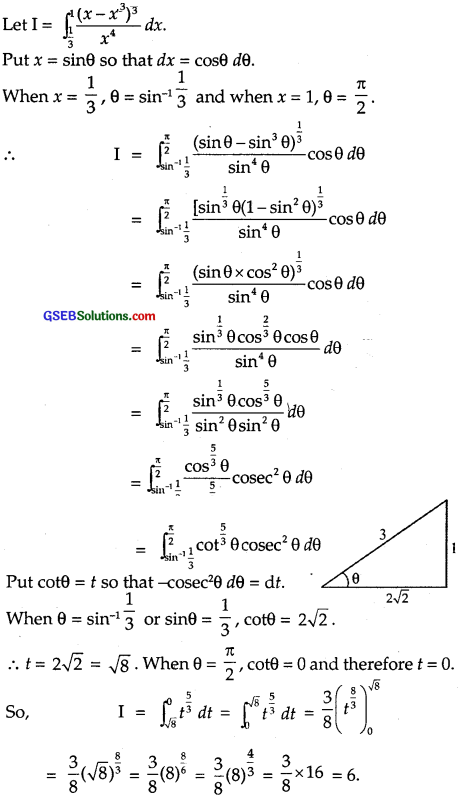
∴ Part (A) is the correct answer.

Question 10.
If f(x) = $\int_{0}^{x}$ tsint dt, then f'(x) is
(A) cos x + x sin x
(B) x sin x
(C) x cos x
(D) sin x + x cos x
Solution:
R.H.S. = f(x) = $\int_{0}^{x}$ tsint dt
Integrating, by parts taking t as first function, we get

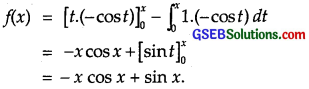
∴ f'(x) = – [1.cos x – x sin x] + cos x = x sin x.
∴ Part (B) is the correct answer.