GSEB Solutions Class 12 Maths Chapter 4 Determinants Miscellaneous Exercise

Gujarat Board GSEB Textbook Solutions Class 12 Maths Chapter 4 Determinants Miscellaneous Exercise Textbook Questions and Answers.

Gujarat Board Textbook Solutions Class 12 Maths Chapter 4 Determinants Miscellaneous Exercise

Question 1.
Prove that the determinant \(\left|\begin{array}{ccc}
x & \sin \theta & \cos \theta \\
-\sin \theta & -x & 1 \\
\cos \theta & 1 & x
\end{array}\right|\) independent of θ.
Solution:
Let ∆ = \(\left|\begin{array}{ccc}
x & \sin \theta & \cos \theta \\
-\sin \theta & -x & 1 \\
\cos \theta & 1 & x
\end{array}\right|\)
Expanding with the help of elements of I row, we get
∆ = x\(\left|\begin{array}{cc} -x & 1 \\ 1 & x \end{array}\right|\) – sin θ \(\left|\begin{array}{cc} -\sin \theta & 1 \\ \cos \theta & x \end{array}\right|\) + cos θ\(\left|\begin{array}{cc}
-\sin \theta & -x \\
\cos \theta & 1
\end{array}\right|\)
= x (- x² – 1) – sin θ (- x sin θ – cos θ) + cos θ (- sin θ + x cos θ)
= – x³ – x + x sin²θ + sin θ cos θ – sin θ cos θ + x cos² θ
= – x³ – x + x (sin² θ + cos² θ) = – x³ – x + x = – x³,
which is independent of θ.

Question 2.
Without expanding the determinant, prove that
\(\left|\begin{array}{lll}
a & a^{2} & b c \\
b & b^{2} & c a \\
c & c^{2} & a b
\end{array}\right|\) = \(\left|\begin{array}{lll}
1 & a^{2} & a^{3} \\
1 & b^{2} & b^{3} \\
1 & c^{2} & c^{3}
\end{array}\right|\)
Solution:
Let ∆ = \(\left|\begin{array}{lll}
a & a^{2} & b c \\
b & b^{2} & c a \\
c & c^{2} & a b
\end{array}\right|\).
Multiply R₁, R₂ and R₃ by a, b and c respectively and then dividing the determined by abc, we get

Question 3.
Evaluate
\(\left|\begin{array}{ccc}
\cos \alpha \cos \beta & \cos \alpha \sin \beta & -\sin \alpha \\
-\sin \beta & \cos \beta & 0 \\
\sin \alpha \cos \beta & \sin \alpha \sin \beta & \cos \alpha
\end{array}\right|\)
Solution:
∆ = \(\left|\begin{array}{ccc}
\cos \alpha \cos \beta & \cos \alpha \sin \beta & -\sin \alpha \\
-\sin \beta & \cos \beta & 0 \\
\sin \alpha \cos \beta & \sin \alpha \sin \beta & \cos \alpha
\end{array}\right|\)
Taking out cos a common from I row and sin α common from III row, we get

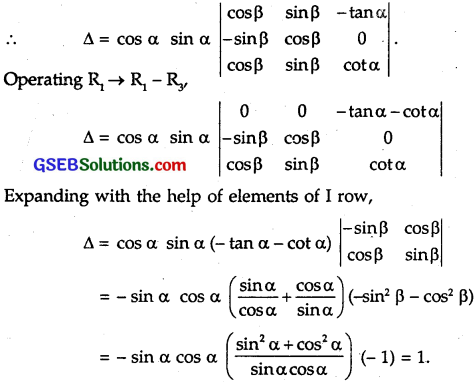
Question 4.
If a, b and c are reals and
∆ = \(\left|\begin{array}{lll}
b+c & c+a & a+b \\
c+a & a+b & b+c \\
a+b & b+c & c+a
\end{array}\right|\) = 0,
show that either a + b + c = 0 or a = b = c
Solution:
∆ = \(\left|\begin{array}{lll}
b+c & c+a & a+b \\
c+a & a+b & b+c \\
a+b & b+c & c+a
\end{array}\right|\).
Operating C₁ → C₁ + C₂ + C₃, we get
∆ = \(\left|\begin{array}{ccc}
2(a+b+c) & c+a & a+b \\
2(a+b+c) & a+b & b+c \\
2(a+b+c) & b+c & c+a
\end{array}\right|\) = 2\(\left|\begin{array}{ccc}
a+b+c & c+a & a+b \\
a+b+c & a+b & b+c \\
a+b+c & b+c & c+a
\end{array}\right|\)
Operating C₂ → C₂ – C₁, C₃ → C₃ – C₁, we get
∆ = 2 \(\left|\begin{array}{lll}
a+b+c & -b & -c \\
a+b+c & -c & -a \\
a+b+c & -a & -b
\end{array}\right|\)
Taking out (a + b + c) common from C₁(- 1) from C₂ and C₃ we get
∆ = 2 (a + b + c) \(\left|\begin{array}{lll}
1 & b & c \\
1 & c & a \\
1 & a & b
\end{array}\right|\).
Expanding with the help of elements of I column, we get
∆ = 2 (a + b + c) [(c b- a²) – (b² – ac) + (ab – c²)]
= 2 (a + b + c)[-(a²- bc) – (b² – ca) – (c² – ab)]
= – (a+ b + c) [2a² + 2b² + 2c² – 2 bc – 2 ca – 2 ab]
= – (a + b + c) [(a – b)² + (b – c)² + (c – a)²]
Now ∆ = 0, when either (a + b + c) = 0
or (a – b)² + (b – c)² + (c – a)² = 0
⇒ a = b = c.
Hence ∆ = 0, when either a + b + c = 0 or a = b = c.

Question 5.
Solve the equation \(\left|\begin{array}{ccc}
x+a & x & x \\
x & x+a & x \\
x & x & x+a
\end{array}\right|\) = 0, a ≠ 0.
Solution:
∆ = \(\left|\begin{array}{ccc}
x+a & x & x \\
x & x+a & x \\
x & x & x+a
\end{array}\right|\)
Operating C₁ → C₁ + C₂ + C₃, we get
∆ = \(\left|\begin{array}{ccc}
3 x+a & x & x \\
3 x+a & x+a & x \\
3 x+a & x & x+a
\end{array}\right|\)
= (3x + a) \(\left|\begin{array}{ccc}
1 & x & x \\
1 & x+a & x \\
1 & x & x+a
\end{array}\right|\)
Operating R₁ → R₁ – R₂, we get
∆ = (3x + a)\(\left|\begin{array}{ccc}
0 & -a & 0 \\
1 & x+a & x \\
1 & x & x+a
\end{array}\right|\).
Expanding with the help of elements of first row, we get
∆ = (3x + a) .a\(\left|\begin{array}{cc}
1 & x \\
1 & x+a
\end{array}\right|\) = a (3x + a) (x + a – x)
= a³(3x + a).
But ∆ = 0 ∴ a²(3x + a).
Also, a ≠ 0 ∴ 3x + a = 0
or x = – \(\frac { a }{ 3 }\).

Question 6.
Prove that \(\left|\begin{array}{ccc}
a^{2} & b c & a c+c^{2} \\
a^{2}+a b & b^{2} & a c \\
a b & b^{2}+b c & c^{2}
\end{array}\right|\) = 4a² b² c².
Solution:
L.H.S = ∆ = \(\left|\begin{array}{ccc}
a^{2} & b c & a c+c^{2} \\
a^{2}+a b & b^{2} & a c \\
a b & b^{2}+b c & c^{2}
\end{array}\right|\).
Taking out a common from C₁, b from C₂ and c from C₃, we get

Taking out – a and – b common from C₂ and C₃, we get
∆ = 2a²b²c\(\left|\begin{array}{lll}
a+c & 1 & 0 \\
a+b & 1 & 1 \\
b+c & 0 & 1
\end{array}\right|\)
Expanding with the help of elements of C₃, we get
∆ = 2a² b²c [b + c + (a + c) – (a + b)]
= 2a²b²c.2c = 4a² b² c² = R.H.S.

Question 7.
If A^-1 = \(\left[\begin{array}{ccc}
3 & -1 & 1 \\
-15 & 6 & -5 \\
5 & -2 & 2
\end{array}\right]\) and B = \(\left[\begin{array}{ccc}
1 & 2 & -2 \\
-1 & 3 & 0 \\
0 & -2 & 1
\end{array}\right]\), find (AB)^-1.
Solution:

Question 8.
Let A = \(\left[\begin{array}{ccc}
1 & -2 & 1 \\
-2 & 3 & 1 \\
1 & 1 & 5
\end{array}\right]\). Verify that
(i) [adj A]^-1 = adj(A^-1), (ii) (A^-1)^-1 = A.
Solution:


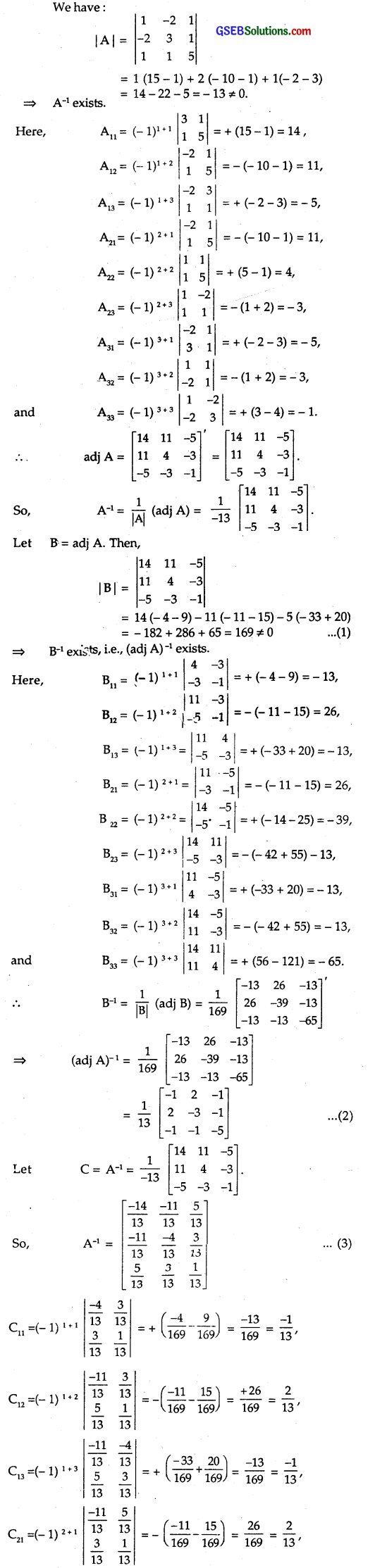
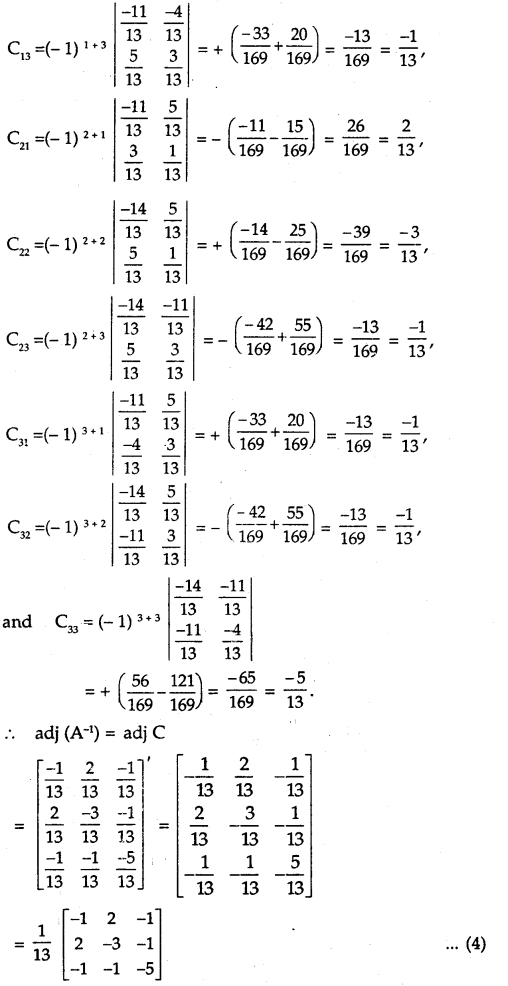
From (2) and (4), we have :
(adj A)^-1 = adj (A^-1),

(ii) From part (i) A^-1 = C (Say)

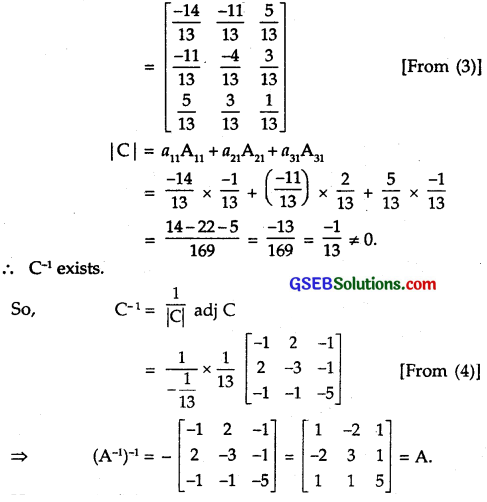
Hence, (A^-1)^-1 = A.

Question 9.
Evaluate \(\left|\begin{array}{ccc}
x & y & x+y \\
y & x+y & x \\
x+y & x & y
\end{array}\right|\)
Solution:
Let ∆ = \(\left|\begin{array}{ccc}
x & y & x+y \\
y & x+y & x \\
x+y & x & y
\end{array}\right|\)
Applying C₁ → C₁ + C₂ + C₃, we get
∆ = \(\left|\begin{array}{ccc}
2(x+y) & y & x+y \\
2(x+y) & x+y & x \\
2(x+y) & x & y
\end{array}\right|\)
Taking out 2(x + y) common from C₁, we get
∆ = 2 (x + y)
\(\left|\begin{array}{ccc}
1 & y & x+y \\
1 & x+y & x \\
1 & x & y
\end{array}\right|\)
Applying R₁ → R₂ – R₁ and R₃ → R₃ – R₁, we get
∆ = 2 (x + y)\(\left|\begin{array}{ccc}
1 & y & x+y \\
0 & x & -y \\
0 & x-y & -x
\end{array}\right|\)
Expanding by Cj, we get
∆ = 2 (x + y) [x (- x) – (- y)(x – y)]
= 2(x + y) [- x² + xy – y²] = – 2(x³ + y³).

Question 10.
Evaluate \(\left|\begin{array}{ccc}
1 & x & y \\
1 & x+y & y \\
1 & x & x+y
\end{array}\right|\)
Solution:
Let ∆ = \(\left|\begin{array}{ccc}
1 & x & y \\
1 & x+y & y \\
1 & x & x+y
\end{array}\right|\)
Applying R₂ → R₂ – R₁ and R₃ → R₃ – R₁, we get
∆ = \(\left|\begin{array}{lll}
1 & x & y \\
0 & y & 0 \\
0 & 0 & x
\end{array}\right|\) = 1 x y x x = xy.

Question 11.
\(\left|\begin{array}{lll}
\alpha & \alpha^{2} & \beta+\gamma \\
\beta & \beta^{2} & \gamma+\alpha \\
\gamma & \gamma^{2} & \alpha+\beta
\end{array}\right|\) = (α – γ) ( γ – α) (α – ß) (α + ß + γ)
Solution:

Question 12.
\(\left|\begin{array}{ccc}
x & x^{2} & 1+p x^{3} \\
y & y^{2} & 1+p y^{3} \\
z & z^{2} & 1+p z^{3}
\end{array}\right|\) = (1 + pxyz)(x – y)(y – z)(z – x), where p is any scalar.
Solution:

Applying R₁ → R₁ – R₂ and R₂ → R₂ – R₃, we get
∆ = (1 + pxyz)\(\left|\begin{array}{ccc}
0 & x-y & x^{2}-y^{2} \\
0 & y-z & y^{2}-z^{2} \\
1 & z & z^{2}
\end{array}\right|\)
Taking out common x-y from R x, y – z from R₂ we get
∆ = (1 + pxyz) (x – y)(y – z)\(\left|\begin{array}{ccc}
0 & 1 & x+y \\
0 & 1 & y+z \\
1 & 2 & z^{2}
\end{array}\right|\)
= (1 + pxyz) (y + z – x – y)
= (1 + pxyz) (x – y)(y – z)(z – x) = R.H.S.

Question 13.
\(\left|\begin{array}{ccc}
3 a & -a+b & -a+c \\
-b+a & 3 b & -b+c \\
-c+a & -c+b & 3 c
\end{array}\right|\) = 3 (a + b + c) (ab + bc + ca)
Solution:

Expanding by C₁, we get
∆ = (a + b + c) [(2b + a) (2c + a) – (a – c) (a – b)]
= (a + b + c)(4bc + 2ab + 2ac + a² – a² + ab + ac – bc)
= (a + b + c) (3ab + 3be + 3ca)
= 3 (a + b + c) (ab + ba + ca) = R.H.S.

Question 14.
\(\left|\begin{array}{ccc}
1 & 1+p & 1+p+q \\
2 & 3+2 p & 4+3 p+2 q \\
3 & 6+3 p & 10+6 p+3 q
\end{array}\right|\) = 1
Solution:
Let ∆ = \(\left|\begin{array}{ccc}
1 & 1+p & 1+p+q \\
2 & 3+2 p & 4+3 p+2 q \\
3 & 6+3 p & 10+6 p+3 q
\end{array}\right|\)
Applying R₂ → R₂ – 2R₁ and R₃ → R₃ – 3R₁, we get
∆ = \(\left|\begin{array}{ccc}
1 & 1+p & 1+p+q \\
0 & 1 & 2+p \\
0 & 3 & 7+3 p
\end{array}\right|\)
= 1 (7 + 3p – 6 – 3p) = 1 (1) = 1. (Expanding by C₁)
= R.H.S.

Question 15.
\(\left|\begin{array}{lll}
\sin \alpha & \cos \alpha & \cos (\alpha+\delta) \\
\sin \beta & \cos \beta & \cos (\beta+\delta) \\
\sin \gamma & \cos \gamma & \cos (\gamma+\delta)
\end{array}\right|\) = 0
Solution:

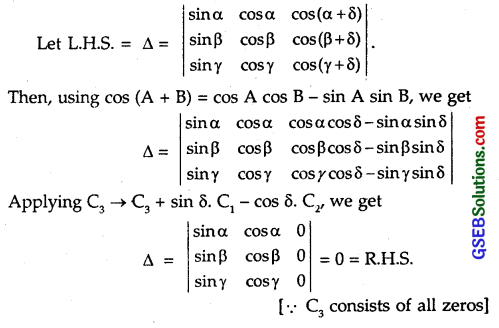
Question 16.
Solve the system of equations
\(\frac { 2 }{ x }\) + \(\frac { 3 }{ y }\) + \(\frac { 10 }{ z }\) = 4
\(\frac { 4 }{ x }\) – \(\frac { 6 }{ y }\) + \(\frac { 5 }{ z }\) = 1
\(\frac { 6 }{ x }\) + \(\frac { 9 }{ y }\) – \(\frac { 20 }{ z }\) = 2
Solution:
Let \(\frac { 1 }{ x }\) = u, \(\frac { 1 }{ y }\) = v, \(\frac { 1 }{ z }\) = w
∴ System of equations is
2u + 3v + 10w = 4
4u – 6v + 5w = 1
6u + 9v – 20w = 2,
which may be written as AX = B,
where A = \(\left[\begin{array}{ccc}
2 & 3 & 10 \\
4 & -6 & 5 \\
6 & 9 & -20
\end{array}\right]\), X = \(\left[\begin{array}{l}
u \\
v \\
w
\end{array}\right]\) + \(\left[\begin{array}{l}
4 \\
1 \\
2
\end{array}\right]\)
To find adj A, we find the cofactors of each of the elements:

Hence, x = 2, y = 3, z = 5

Question 17.
If a, b, c are in A. P., then the determinant \(\left|\begin{array}{ccc}
x+2 & x+3 & x+2 a \\
x+3 & x+4 & x+2 b \\
x+4 & x+5 & x+2 c
\end{array}\right|\) is equal to
(A) 0
(B) 1
(C) x
(D) 2a
Solution:

Question 18.
If x, y, z are non-zero real numbers, then the inverse of the matrix A = \(\left(\begin{array}{lll}
x & 0 & 0 \\
0 & y & 0 \\
0 & 0 & z
\end{array}\right)\) is
(A) \(\left(\begin{array}{ccc}
x^{-1} & 0 & 0 \\
0 & y^{-1} & 0 \\
0 & 0 & z^{-1}
\end{array}\right)\)
(B) xyz\(\left(\begin{array}{ccc}
x^{-1} & 0 & 0 \\
0 & y^{-1} & 0 \\
0 & 0 & z^{-1}
\end{array}\right)\)
(C) \(\frac { 1 }{ xyz }\) \(\left(\begin{array}{lll}
x & 0 & 0 \\
0 & y & 0 \\
1 & 0 & z
\end{array}\right)\)
(D) \(\frac { 1 }{ xyz }\)\(\left(\begin{array}{lll}
1 & 0 & 0 \\
0 & 1 & 0 \\
1 & 0 & 1
\end{array}\right)\)
Solution:
\(\left(\begin{array}{lll}
x & 0 & 0 \\
0 & y & 0 \\
0 & 0 & z
\end{array}\right)\)
The cofactors of the elements are

∴ Part (A) is the required answer.

Question 19.
Let A = \(\left[\begin{array}{ccc}
1 & \sin \theta & 1 \\
-\sin \theta & 1 & \sin \theta \\
-1 & -\sin \theta & 1
\end{array}\right]\), where 0 ≤ θ ≤ 2π, then
(A) Det (A) = 0
(B) Det A ∈ (2, ∞)
(C) Det (A) ∈ (2, 4)
(D) Det (A) ∈ [2,4]
Solution:
A = \(\left[\begin{array}{ccc}
1 & \sin \theta & 1 \\
-\sin \theta & 1 & \sin \theta \\
-1 & -\sin \theta & 1
\end{array}\right]\)
So, Det A = \(\left|\begin{array}{ccc}
1 & \sin \theta & 1 \\
-\sin \theta & 1 & \sin \theta \\
-1 & -\sin \theta & 1
\end{array}\right|\),
= 1 . (1 + sin² θ) – sin θ (- sin θ + sin θ) + 1 . (sin² θ + 1)
= 2 (1 + sin² θ)
For θ = 0, π, 2π, Det A = 2.
For θ = \(\frac { π }{ 2 }\), \(\frac { 3π }{ 2 }\), Det A = 2. (1 + 1) = 4.
⇒ Part (D) is the correct answer.