This GSEB Class 10 Maths Notes Chapter 2 બહુપદીઓ covers all the important topics and concepts as mentioned in the chapter.
બહુપદીઓ Class 10 GSEB Notes
→ એક બહુપદી anxn + an-1xn-1 + … a1x + a0 ; an ≠ 0 a0; a1 a2,……….. an અચળ હોય ત્યારે આ સ્વરૂપે દર્શાવાતી પદાવલિને ચલ xમાં બહુપદી કહે છે. જ્યાં, n પૂર્ણ સંખ્યા છે.
→ એક બહુપદીની ઘાત જો p (x) એ માં બહુપદી હોય, તો p(x)માં ના મહત્તમ ઘાતાંકને બહુપદી p(x)ની ઘાત કહે છે.
→ એક ઘાતવાળી બહુપદીને સુરેખ બહુપદી (Linear polynomial) કહે છે. દા. ત., 2x + 5, √5x + 3.7, πt + 9 વગેરે સુરેખ બહુપદીઓ છે. ચલ ની સુરેખ બહુપદીનું વ્યાપક સ્વરૂપ ax + b છે. જ્યાં, વ અને b વાસ્તવિક સંખ્યાઓ છે તથા a ≠ 0.
![]()
→ જે બહુપદીની ઘાત 2 હોય, તે બહુપદીને દ્વિઘાત બહુપદી કહે છે. દા. ત., 2x2 + 5x + 2, 9y2 – 1, √8x2 + 3x + 5 વગેરે દ્વિઘાત બહુપદીઓ છે. ચલ ની દ્વિઘાત બહુપદીનું વ્યાપક સ્વરૂપ ax2 + bx + c છે. જ્યાં, a, b અને C વાસ્તવિક સંખ્યાઓ છે તથા a ≠ 0.
→ જે બહુપદીની ઘાત 3 હોય, તે બહુપદીને ત્રિઘાત બહુપદી કહે છે. દા. ત., x3 – 3x2 + 5x – 3, 27t3 – 8, 3x3 + 11x2 + 5 વગેરે ત્રિઘાત બહુપદીઓ છે. ચલ ની ત્રિઘાત બહુપદીનું વ્યાપક સ્વરૂપ ax3 + bx2 + cx + d છે. જ્યાં, a, b, C અને તે વાસ્તવિક સંખ્યાઓ છે તથા a ≠ 0.
→ બહુપદી p(x)નું x = k આગળનું મૂલ્ય (કિંમત) જો p (x) એ xમાં બહુપદી હોય અને જો k કોઈ વાસ્તવિક સંખ્યા હોય, તો p (x)માં ને બદલે k મૂકવાથી મળતા મૂલ્યને p (x)ની x = k આગળની કિંમત (મૂલ્ય) કહે છે અને તેને p (k) વડે દર્શાવાય છે.
→ બહુપદીનું શૂન્યઃ જો p (k) = 0 હોય, તો વાસ્તવિક સંખ્યા ને બહુપદી p (x)નું શૂન્ય કહે છે..
દા. ત., બહુપદી p (x) = x 2 – 3x + 2 માટે p(1) = (1)2 – 3 (1)2 + 2 = 1 – 3 + 2 = 0 અને
p (2) = (2)2 – 3 (2) + 2 = 4 – 6 + 2 = 0.
આથી 1 અને 2 એ બહુપદી p (x) = x2 – 3x + 2નાં શૂન્યો છે.
→ એક શૂન્યોની સંખ્યા સુરેખ બહુપદી p (x) = ax + bનું ફક્ત એક જ શૂન્ય છે.

દ્વિઘાત બહુપદીનાં વધુમાં વધુ બે શુન્યો હોય અને ત્રિઘાત બહુપદીનાં વધુમાં વધુ ત્રણ શૂન્યો હોય.
→ બહુપદીનાં શૂન્યોનો ભૌમિતિક અર્થ સુરેખ બહુપદી ax + b, a ≠ 0 માટે y = ax + bનો આલેખ -અક્ષને બરાબર એક બિંદુ (\(\frac{-b}{a}\)) માં છેદતી રેખા છે.
→ આથી શૂન્યતર a માટે સુરેખ બહુપદી ax + bને એક જ શૂન્ય \(\frac{-b}{a}\) છે અને તે y = ax + bનો આલેખ x-અક્ષને જે બિંદુએ છેદે છે તેનો xયામ છે.
→ શૂન્યતર a હોય તેવી કોઈ પણ દ્વિઘાત બહુપદી ax2 + bx + cના સંદર્ભમાં તેને અનુરૂપ સમીકરણ y = ax2 + bx + cનો આલેખ અનુક્રમે a > 0 અથવા a < 0 – અનુસાર ઉપરની તરફ ખુલ્લો વક્ર અથવા નીચેની તરફ ખુલ્લો વક્ર મળશે. (આ વક્રને પરવલય કહે છે.)
→ દ્વિઘાત બહુપદી ax2 + bx + c, a≠ 0 નાં શૂન્યો એ નિશ્ચિતપણે y = a2 + bx + cને દર્શાવતો પરવલય ૮-અક્ષને જે બિંદુઓમાં છેદે છે તે બિંદુઓના xયામ થાય.
→ બહુપદીઓ U = ax2 + bx + c, a $ 0ના આલેખ (પરવલય) અને ૮-અક્ષના છેદ માટે નીચે મુજબના ત્રણ વિકલ્પ હોઈ શકે?
(1) y = ax2 + bx + cને દર્શાવતો પરવલય x-અક્ષને બે ભિન્ન બિંદુઓમાં છેદે. આ કિસ્સામાં પરવલય અને x-અક્ષના બે છેદબિંદુઓનાં xયામ એ ax + bx + cનાં બે શૂન્યો થાય.
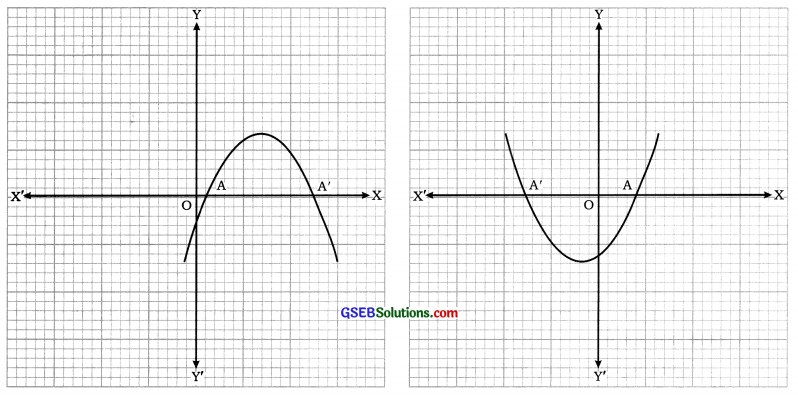
![]()
(2) y = ax2 + bx + cને દર્શાવતો પરવલય x-અક્ષને એક જ બિંદુમાં છેદે (સ્પર્શે). આ કિસ્સામાં પરવલય અને ૮-અક્ષના સ્પર્શબિંદુનો xયામ એ ax2 + bx + cનું એકમાત્ર શૂન્ય થાય.
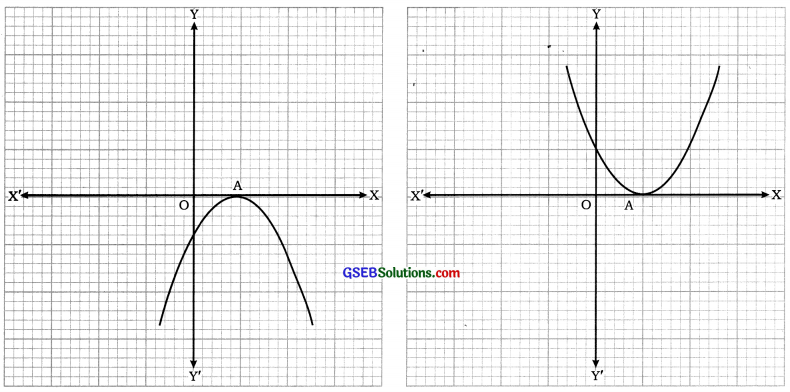
(3) y = ax2 + bx + cને દર્શાવતો પરવલય x-અક્ષને છેદે નહીં. આ કિસ્સામાં ax2 + bx + cને એક પણ શૂન્ય નથી.
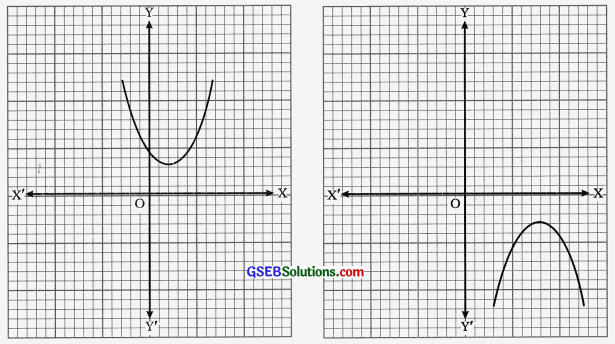
આ જ રીતે, કોઈ પણ ઘાતની બહુપદી p (X)નાં શૂન્યો y = p (x)નો આલેખ -અક્ષને જે બિંદુઓમાં છેદે તે બિંદુઓનાં xયામ દ્વારા મળે છે.
→ દ્વિઘાત બહુપદીની માફક, ત્રિઘાત બહુપદી p(X) માટે y = p (x)નો આલેખ x-અક્ષને 0, 1, 2 અથવા 3 બિંદુઓમાં છે અને તે મુજબ ત્રિઘાત બહુપદીનાં 0, 1, 2 અથવા 3 શૂન્યો મળે.
→ બહુપદીનાં શૂન્યો અને સહગુણકો વચ્ચેનો સંબંધ દ્વિઘાત બહુપદીઃ જો α (આલ્ફા) અને β (બીટા) એ દ્વિઘાત બહુપદી p (x) = ax2 + bx + c, a ≠ 0નાં શૂન્યો હોય, તો
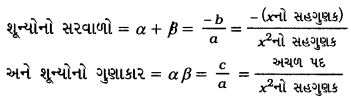
દા. ત., આગળ આપણે જોયું કે, α = 1 અને β = 2 એ બહુપદી p(x) = x2 – 3x + 2નાં બે શૂન્યો છે.

પ્રતીપ તરીકે, જો અને B એ કોઈ દ્વિઘાત બહુપદીનાં શૂન્યો હોય તેવી બહુપદી p (x) = x2 – (α + β) + αβ દ્વારા મળે. વિસ્તૃતરૂપે તે બહુપદીને
p(x) = x2 – (α + β)x + αβ}, જ્યાં k કોઈ પણ શૂન્યતર વાસ્તવિક સંખ્યા છે, ના સ્વરૂપે દર્શાવી શકાય.
→ જો α અને β એ દ્વિઘાત બહુપદી ax2 + bx + cનાં શૂન્યો હોય અને
- જો α તથા β વિરોધી સંખ્યાઓ હોય, તો b = 0
- જો α તુ અને β પરસ્પરના વ્યસ્ત હોય, તો c = a.
![]()
→ ત્રિઘાત બહુપદીઃ જો α, β અને γ (ગેમા) એ ત્રિઘાત
બહુપદી ax2 + bx + cx + d, a ≠ 0નાં શૂન્યો હોય, તો
શૂન્યોનો સરવાળો = α + β + γ

દા. ત., ત્રિઘાત બહુપદી p (x) = x3 – 6x2 + 11x – 6 માટે,
p(1) = 1 – 6 + 11 – 6 = 0,
p (2) = 8 – 24 + 22 – 6 = 0 અને
p (3) = 27 – 54 + 33 – 6 = 0.
આથી α = 1, β = 2 અને γ = 3 એ ત્રિઘાત બહુપદી p(x) = x3 – 6x2 + 11x – 6નાં શૂન્યો છે.

→ α, β અને γ જે ત્રિઘાત બહુપદીનાં શૂન્યો છે, તે બહુપદી k[x3 – (α + β + γ) + (αβ + βγ + γα)x – αβγ] દ્વારા મળે છે. જ્યાં, k કોઈ પણ શૂન્યતર વાસ્તવિક સંખ્યા છે.
→ બહુપદીનાં શૂન્યો અને અવયવોઃ જો p (x)નાં શૂન્યો પૈકી કોઈ એક શૂન્ય વ હોય, તો x – o એ p (x)નો એક અવયવ છે. જો વ અને b એ બહુપદી p(x)નાં બે શુન્યો હોય, તો (x – a) (x – b) = x – (a + b)x + ab એ બહુપદી p(x)નો અવયવ છે.
→ આગળના ધોરણમાં ભણી ગયેલ અગત્યના નિત્યસમો:
- (x + a) (x + b) = x2 + (a + b)x + ab
- (x ± y) = x2 ± 2xy + y2
- (x + y)(x – y) = x2 – y2
- (x + y + z)2 = x2 + y2 + y2 + 2xy + 2yz + 2zx
- (x + y)3 = x3 + y3 + 3xy(x + y)
= x3 + 3x2y + 3xy2 + y3 - (x – y)3 = x3 – y3 – 3xy(x – y)
= x3 – 3x2y + 3xy2 – y3 - x3 + y3 + z3 – 3xyz = (x + y + z)(x2 + y2 + z2 – xy – yz – zx)
→ બહુપદીઓ માટે ભાગપ્રવિધિઃ જો p (x) અને g (x) બે બહુપદીઓ હોય અને q (x) ≠ 0, તો આપણે એવી બહુપદીઓ q (x) અને r (x) શોધી શકીએ,
જેથી p (x) = g (x) × q (x) + f (x), જ્યાં, r (x) = 0 અથવા r (x)ની ઘાત < g (x)ની ઘાત.
અહીં, p (x) એ ભાજ્ય છે, g(x) એ ભાજક છે, q (x) એ ભાગફળ છે અને r (x) એ શેષ છે.
જો r(x) = 0, તો g (x) તેમજ q (x) એ p (x)ના અવયવો છે.
જો કોઈ વાસ્તવિક સંખ્યા ઘ એ બહુપદી p (x)નું શૂન્ય હોય, તો અવયવ પ્રમેય, પ્રમેય મુજબ (x – a) એ p (x)નો અવયવ છે.
→ એક બહુપદીનો બીજી બહુપદી વડે ભાગાકારઃ
- એક બહુપદીનો બીજી બહુપદી માટે ભાગાકાર કરવા માટે ભાજ્ય બહુપદી p(x)ની ઘાત એ ભાજક g (x)ની ઘાત કરતાં અધિક અથવા સરખી હોવી જોઈએ. એટલે કે, p(x)ની ઘાત ≥ g (x)ની ઘાત.
- ભાજ્ય બહુપદી p (x) તેમજ ભાજક બહુપદી g (x)ને પ્રમાણિત સ્વરૂપમાં લખો, એટલે કે બંનેમાં રહેલ કોઈ એક ચલના ઘાતાંકના ઊતરતા ક્રમમાં પદોની ગોઠવણી કરો.
- ભાજ્યના પ્રથમ પદને ભાજકના પ્રથમ પદ વડે ભાગી ભાગફળનું પ્રથમ પદ મેળવો.
- ભાજક બહુપદી g (x) ના દરેક પદને ભાગફળના પ્રથમ પદ વડે ગુણીને તે ગુણાકાર ભાજ્ય બહુપદી p (x)માંથી બાદ કરીને નવી ભાજ્ય બહુપદી મેળવો.
- સોપાન (3) અને (4)નું ત્યાં સુધી પુનરાવર્તન કરો જ્યાં સુધી મળતી નવી ભાજ્ય બહુપદીની ઘાત ભાજક બહુપદીની વાત કરતાં ઓછી હોય અથવા નવી ભાજ્ય બહુપદી 0 હોય. જવાબ તરીકે ભાગફળ બહુપદી અને શેષ બહુપદી દર્શાવવામાં આવશે.
→ p (x) = g (x) = q (x) + r (x) એ પરિણામ બહુપદીઓ માટે ભાગપ્રવિધિ તરીકે ઓળખાય છે. અહીં, આપેલ ચાર રાશિઓ પૈકી કોઈ પણ ત્રણ રાશિ આપેલ હોય, તો સમીકરણની બંને બાજુના પદોમાં સરખી ઘાતવાળા પદોના સહગુણકોની સરખામણી કરવાથી અજ્ઞાત ચોથી રાશિ શોધી શકાય.
→ 1, 2 અને 3 ઘાત ધરાવતી બહુપદીઓને અનુક્રમે સુરેખ, દ્વિઘાત અને ત્રિઘાત બહુપદીઓ કહે છે.
→ વાસ્તવિક સંખ્યાઓ a, b, c તથા શૂન્યતર વ માટે, x પરની વાસ્તવિક સહગુણકો ધરાવતી દ્વિઘાત બહુપદી ax + bx + c છે.
→ જો p (c) = 0 હોય, તો વાસ્તવિક સંખ્યા મને બહુપદી p (2) નું શૂન્ય કહે છે.
→ જ્યાં, U = p (x)નો આલેખ -અક્ષને છેદે છે તે બિંદુના xયામ એ બહુપદી p (x)નાં શૂન્યો છે. દ્વિઘાત બહુપદીને વધુમાં વધુ 2 વાસ્તવિક શૂન્યો અને ત્રિઘાત બહુપદીને વધુમાં વધુ 3 વાસ્તવિક શૂન્યો હોય છે.
→ જો ઘ અને B એ દ્વિઘાત બહુપદી ax2 + bx + cનાં શૂન્યો
હોય, તો α + β = \(\frac{-b}{a}\) , αβ = \(\frac{c}{a}\).
![]()
→ જો α, β, Y એ ત્રિઘાત બહુપદી ax3 + bx2 + cx + d નાં શૂન્યો હોય, તો α + β + γ = \(\frac{-b}{a}\) , αβ + βγ + γα = \(\frac{c}{a}\) અને αβγ = \(\frac{-d}{a}\)
→ ભાગપ્રવિધિ દર્શાવે છે કે, આપેલ કોઈ બહુપદી p(x) અને કોઈ શૂન્યતર બહુપદી g (x)ને સંગત બહુપદીઓ q (C) અને r(x) મળે જેથી, p(x) = g (x) q (x) + f (x); જ્યાં, r (x) = 0 અથવા r (x)ની ઘાત < g (x)ની ઘાત.