This GSEB Class 10 Maths Notes Chapter 1 વાસ્તવિક સંખ્યાઓ covers all the important topics and concepts as mentioned in the chapter.
વાસ્તવિક સંખ્યાઓ Class 10 GSEB Notes
→ તમે વાસ્તવિક સંખ્યાઓની દુનિયામાં ડોકિયું કર્યું અને તમને અસંમેય સંખ્યાઓ મળી. આ પ્રકરણમાં આપણે વાસ્તવિક સંખ્યાઓની ચર્ચા ચાલુ રાખીશું. આપણે 1.2 અને 1.3માં ધન પૂર્ણાકોના ખૂબ જ અગત્યના ગુણધર્મો, યુક્લિડની ભાગપ્રવિધિ અને અંકગણિતના મૂળભૂત પ્રમેયથી પ્રારંભ કરીશું.
→ યુક્લિડની ભાગપ્રવિધિ” નામ જ દર્શાવે છે કે તેને પૂર્ણાકોની વિભાજ્યતા સાથે કંઈક સંબંધ છે. સરળ ભાષામાં કહીએ તો, કોઈ પણ ધન પૂર્ણાક વને બીજા કોઈ ધન પૂર્ણાક b વડે ભાગવામાં આવે તો અનૃણ શેષ r વધે અને તે b કરતાં નાની હોય. તમારામાંથી મોટા ભાગના અભ્યાસાથી કદાચ ભાગાકારને સ્વાભાવિક લાંબી પ્રક્રિયા તરીકે ઓળખતા હશે. જોકે આ પરિણામ ખૂબ જ સરળતાથી દર્શાવી અને સમજી શકાય છતાં પૂર્ણાકોની વિભાજ્યતાના ગુણધર્મો-સંબંધી ઘણા બધા ઉપયોગો છે. આપણે તેમાંના કેટલાકને સમજીશું અને તેનો ઉપયોગ મુખ્યત્વે બે ધન પૂર્ણાકોના ગુ.સા.અ. શોધવા માટે કરીશું.
→ અન્ય પાસામાં અંકગણિતના મૂળભૂત પ્રમેયમાં ધન પૂર્ણાકોના ગુણાકારની વાત આવે છે. તમે જાણો છો કે દરેક વિભાજ્ય પૂર્ણાકને અવિભાજ્ય પૂર્ણાકોના ગુણાકાર તરીકે અનન્ય રીતે દર્શાવી શકાય. આ અગત્યનો ગુણધર્મ એ અંકગણિતનું મૂળભૂત પ્રમેય છે. આ પરિણામ સરળતાથી દર્શાવી અને સમજાવી શકાય. આપણે અંકગણિતના મૂળભૂત પ્રમેયના બે મુખ્ય વ્યવહારુ ઉપયોગ કરીશું. તેના ગણિતના ક્ષેત્રના કેટલાક ખૂબ જ ઊંડા અને નોંધપાત્ર ઉપયોગો છે. તમે ધોરણ IXમાં અભ્યાસ કર્યો છે કે, √2, √3 અને √5 જેવી ઘણી બધી સંખ્યાઓને અસંમેય સાબિત કરવા આ પ્રમેય વપરાય છે. બીજું, આ પ્રમેયનો ઉપયોગ, સંમેય સંખ્યાઓ \(\frac{P}{q}\) (q ≠ 0)ની દશાંશ અભિવ્યક્તિ ક્યારે સાત્ત હોય અને ક્યારે અનંત આવૃત્ત હોય તે જાણવામાં થાય છે. આ માટે આપણે ના છેદ qના અવિભાજ્ય અવયવો પર દષ્ટિપાત કરીએ છીએ. તમે જોશો કે, qનું અવિભાજ્ય અવયવોમાં અવયવીકરણ ની દશાંશ અભિવ્યક્તિનું સંપૂર્ણ સ્વરૂપ નક્કી કરે છે.
![]()
→ આપણે જાણીએ છીએ કે, ગણતરીની સંખ્યાઓ 1, 2, 3, 4… વગેરેને પ્રાકૃતિક સંખ્યાઓ કહે છે અને તેમના સમૂહને N દ્વારા દર્શાવવામાં આવે છે.
આમ, N = {1, 2, 3, 4, }.
→ પ્રાકૃતિક સંખ્યાઓને ધન પૂર્ણાકો પણ કહે છે.
→ પ્રાકૃતિક સંખ્યાઓના સમૂહમાં 0(શૂન્ય)નો સમાવેશ કરવાથી આપણને પૂર્ણ સંખ્યાઓ મળે છે. પૂર્ણ સંખ્યાઓના સમૂહને જ દ્વારા દર્શાવવામાં આવે છે.
આમ, x = {0, 1, 2, 3,..}.
→ 0, બધી જ પ્રાકૃતિક સંખ્યાઓ તથા દરેક પ્રાકૃતિક સંખ્યાની વિરોધી સંખ્યાને સમાવતા સમૂહને પૂર્ણાકોનો સમૂહ કહે છે અને તેને 1 અથવા 2 દ્વારા દર્શાવવામાં આવે છે.
આમ, 1 અથવા Z = {…, -2, -1, 0, 1, 2, …}. 0 એ ધન પૂર્ણાંક પણ નથી તેમજ ઋણ પૂર્ણાંક પણ નથી.
→ જે પ્રાકૃતિક સંખ્યાઓને 2 વડે નિઃશેષ ભાગી શકાય છે, તે સંખ્યાઓને યુગ્મ સંખ્યા કહે છે અને તેમના સમૂહને E દ્વારા દર્શાવવામાં આવે છે.
આમ, E = {2, 4, 6, .}.
→ જે પ્રાકૃતિક સંખ્યાઓને 2 વડે નિઃશેષ ભાગી ના શકાય તે સંખ્યાઓને અયુગ્મ સંખ્યા કહે છે અને તેમના સમૂહને 0 દ્વારા દર્શાવવામાં આવે છે.
આમ, 0 = {1, 3, 5, …}.
→ સિવાયની કોઈ પણ પ્રાકૃતિક સંખ્યાના અવયવો જો ફક્ત 1 અને તે સંખ્યા પોતે જ હોય, તો તેવી સંખ્યાને અવિભાજ્ય સંખ્યા અથવા ફક્ત અવિભાજ્ય કહે છે. અવિભાજ્ય સંખ્યાઓના સમૂહને P દ્વારા દર્શાવવામાં આવે છે.
આમ, P = {2, 3, 5, 7, 11, 13, ………….}.
→ યુગ્મ સંખ્યાઓ પૈકી ફક્ત 2 જ અવિભાજ્ય સંખ્યા છે. 2 એ સૌથી નાની અવિભાજ્ય સંખ્યા છે અને જાન્યુઆરી 2019 સુધીમાં શોધાયેલ સૌથી મોટી અવિભાજ્ય સંખ્યા 282,589,933–1 છે. જે 24,862,048 અંકો ધરાવતી સંખ્યા છે. તેનાથી પણ મોટી અવિભાજ્ય સંખ્યાની શોધ અવિરતપણે ચાલુ જ છે.
→ સિવાયની કોઈ પણ પ્રાકૃતિક સંખ્યા જો અવિભાજ્ય ના હોય, તો તેને વિભાજ્ય સંખ્યા અથવા ફક્ત વિભાજ્ય કહે છે. વિભાજ્ય સંખ્યાઓના સમૂહને C દ્વારા દર્શાવવામાં આવે છે.
આમ, C = {4, 6, 8, 9, 10, 12, 14, …………}.
ખાસ નોંધ લેવી કે, 1 એ વિભાજ્ય સંખ્યા પણ નથી કે અવિભાજ્ય સંખ્યા પણ નથી.
→ જે બે પ્રાકૃતિક સંખ્યાઓને 1 સિવાય કોઈ પણ સામાન્ય અવયવ ન હોય તેવી સંખ્યાઓને પરસ્પર અવિભાજ્ય સંખ્યા કહે છે. દા. ત., 8 અને 15 પરસ્પર અવિભાજ્ય છે, પરંતુ 8 અને 12 પરસ્પર અવિભાજ્ય નથી.
→ જે સંખ્યાને \(\frac{P}{q}\) સ્વરૂપમાં (જ્યાં, p અને ૧ પૂણકો છે તથા q ≠ 0) દર્શાવી શકાય તેવી સંખ્યાને સંમેય સંખ્યા કહે છે. સંમેય સંખ્યાઓના સમૂહને Q દ્વારા દર્શાવવામાં આવે છે.
→ જે સંખ્યા સંમેય સંખ્યા નથી તેવી સંખ્યાને અસંમેય સંખ્યા કહે છે. અસંમેય સંખ્યાઓના સમૂહને \(\overline{\mathrm{Q}}\) દ્વારા દર્શાવવામાં આવે છે.
→ બધી જ સંમેય સંખ્યાઓ તેમજ બધી જ અસંમેય સંખ્યાઓના સમૂહને વાસ્તવિક સંખ્યાઓનો સમૂહ કહે છે અને તેને R દ્વારા દર્શાવવામાં આવે છે.
→ યુક્લિડનું ભાગાકારનું પૂર્વપ્રમેય :
પ્રમેય 1.1 (યુક્લિડનું ભાગાકારનું પૂર્વપ્રમેય) આપેલ ધન પૂર્ણાકો ઘ અને મને સંગત અનન્ય અનૃણ પૂર્ણાકો q અને r એવા મળે કે જેથી a = bq + 1, 0 ≤ r < b. નોંધઃ q અનુણ છે, પરંતુ q, a તથા r સાથે શૂન્ય નથી. આ પરિણામ લાંબા સમયથી પ્રચલિત છે, પરંતુ તેની પ્રથમ વખત યુક્લિડ(Euclid)ની Elements Book Viામાં નોંધ લેવાઈ હતી. યુક્લિડની ભાગપ્રવિધિ આ પૂર્વપ્રમેય પર આધારિત છે. કોઈ પણ ધન પૂર્ણાક વને અથવા તેના વર્ગને અથવા ઘનને બીજા કોઈ પૂર્ણાક b દ્વારા ભાગવાથી મળતાં પરિણામો સાબિત કરવામાં લૂ અને જુની અનન્યતા ખૂબ જ ઉપયોગી સાબિત થાય છે. સરળ શબ્દોમાં કહીએ તો, ની કિંમતને અનુરૂપ વની કિંમત નીચેના પૈકી કોઈ
![]()
→ પણ સ્વરૂપમાં લઈ શકાયઃ
- 2k અથવા 2k + 1
- 3k અથવા 3k + 1 અથવા 3k + 2
- 4k અથવા 4k + 1 અથવા 4k + 2 અથવા 4k + 3 વગેરે. જ્યાં, k એ અનૃણ પૂર્ણાક છે.
→ જેના વડે ધન પૂર્ણાકો અને b બંને વિભાજ્ય હોય તેવો મોટામાં મોટો ધન પૂણક d એ વ અને મનો ગુ.સા.અ. છે. → યુક્લિડની ભાગપ્રવિધિ યુક્લિડની ભાગપ્રવિધિ એ આપેલા બે ધન પૂર્ણાકોનો ગુ.સા.અ. શોધવાની પ્રવિધિ છે. c > d હોય તેવા બે ધન પૂર્ણાકો દે અને તેનો ગુ.સા.અ. મેળવવા માટે નીચેનાં સોપાન છેઃ
- સોપાન 1: યુક્લિડના ભાગાકાર પૂર્વપ્રમેયનો : અને ઉપર ઉપયોગ કરતાં, આપણને c = dq + r, 0 ≤ 7 < d થાય તેવી પૂર્ણ સંખ્યાઓ q અને મળે.
- સોપાન 2: જો r = 0, તો તે એ C અને વનો ગુ.સા.અ. થાય. જો r ≠ 0, તો અને અને ભાગાકારનું પૂર્વપ્રમેય – લગાડીએ.
- સોપાન 3: આ પ્રક્રિયા જ્યાં સુધી શેષ 0 ન થાય ત્યાં સુધી ચાલુ રાખો. આ તબક્કે જ્યારે શેષ શૂન્ય બને ત્યારે ભાજક એ માગેલ ગુ.સા.અ. થાય. આ પ્રવિધિમાં પરિણામ મળે છે, કારણ કે ગુ.સા.અ. (c, d) = ગુ.સા.અ. (d, r). ગુ.સા.અ. (c, d) એ અને વનો ગુ.સા.અ. દર્શાવે છે.
→ ઉદાહરણ : યુક્લિડની ભાગપ્રવિધિ દ્વારા 175 અને 112નો ગુ.સા.અ. શોધો.
(1) 175 > 112 હોવાથી આપણે 175 અને 112 માટે ભાગપ્રવિધિનો ઉપયોગ કરીએ તો નીચેનું પરિણામ મળે:
175 = 112 × 1 + 63
(2) શેષ 63 %0 હોવાથી આપણે 112 અને 63 માટે
ભાગપ્રવિધિનો ઉપયોગ કરીએ તો નીચેનું પરિણામ મળે :
112 = 63 × 1 + 49
(3) શેષ 49 8 0 હોવાથી આપણે 63 અને 49 માટે ભાગપ્રવિધિનો ઉપયોગ કરીએ તો નીચેનું પરિણામ મળે ?
63 = 49 × 1 + 14
(4) શેષ 14 હોવાથી આપણે 49 અને 14 માટે ભાગપ્રવિધિનો ઉપયોગ કરીએ તો નીચેનું પરિણામ મળે :
49 = 14 × 3 + 7
(5) શેષ 7 8 9 હોવાથી આપણે 14 અને 7 માટે ભાગપ્રવિધિનો ઉપયોગ કરીએ તો નીચેનું પરિણામ મળે :
14 = 7 × 2 + 0.
(6) હવે શેષ શૂન્ય મળે છે અને હવે આપણે પ્રક્રિયા આગળ નથી કરી શકતા. આ પગલે ભાજક 7 હોવાથી 175 અને 112નો ગુ.સા.અ. 7 છે, એટલે કે ગુ.સા.અ. (175, 112) = 7.
યુક્લિડની ભાગપ્રવિધિ માત્ર ખૂબ જ મોટી સંખ્યાઓના ગુ.સા.અ. મેળવવા માટે જ ઉપયોગી છે એટલું જ નહીં પરંતુ તે કમ્યુટરના પ્રોગ્રામ તૈયાર કરવા માટેના અલ્ગોરિધમ(પ્રવિધિ)નાં ખૂબ જ શરૂઆતનાં ઉદાહરણોમાંની એક છે.
નોંધ:
- યુક્લિડના ભાગાકારનું પૂર્વપ્રમેય અને ભાગપ્રવિધિ ખૂબ જ નજીકથી એકબીજા સાથે જોડાયેલા હોવાથી લોકો અવારનવાર ભાગાકારના પૂર્વપ્રમેયને ભાગાકાર પ્રવિધિ પણ કહેતા હતા.
- વળી, યુક્લિડની ભાગપ્રવિધિનું વિધાન માત્ર ધન પૂર્ણાકો માટે જ કર્યું છે, છતાં તેને b ≠ 0 હોય તેવા બધા જ શૂન્યતર પૂર્ણાકો સુધી વિસ્તારી શકાય, જોકે ભાગપ્રવિધિના આ પાસાની ચર્ચા આપણે અહીં નહીં કરીએ.
![]()
→ a અને ‘ના ગુ.સા.અ. અંગેનું એક અગત્યનું પરિણામ 175 અને 112નો ગુ.સા.અ. શોધવાના ઉપરોક્ત ઉદાહરણમાં સોપાન (4) પરથી
7 = 49 – 14 × 3
= 49 – (63 – 49) × 3. સિોપાન (3) પરથી
= 49-63 × 3 + 49 × 3
= 49 × 4 – 63 × 3.
= (112 – 63) × 4 – 63 × 3 (સોપાન (2) પરથી]
= 112 × 4-63 × 4-63 × 3
= 112 × 4-63 × 7
= 112 × 4 – 175 – 112) × 7 સોપાન (1) પરથી]
= 112 × 4 – 175 × + 112 × 7
= 112 × 11 – 175 17
= 11 × 112 – 7 × 175
આ પરિણામને બીઝૉટનું નિત્યસમ કહે છે. તેના દ્વારા બે સંખ્યાઓના ગુ.સા.અ.ને તે બે સંખ્યાઓના કોઈ ગુણકના તફાવત સ્વરૂપે દર્શાવવામાં આવે છે.
સાંકેતિક રીતે, ગુ.સા.અ. (a, b) = ax – bu, જ્યાં, ૪ અને પુ એ પૂર્ણાકો છે. નોંધ લેશો કે ગુ.સા.અ.
(a, b) = ax – bg અભિવ્યક્તિ અનન્ય નથી, એટલે કે મેળવેલ અભિવ્યક્તિમાં વ x b અથવા તેના ગુણક ઉમેરવા અને બાદ કરવાથી x અને પુની બીજી ઘણી કિંમતો મળી શકે છે.
→ યુક્લિડની ભાગપ્રવિધિનાં કેટલાંક અગત્યનાં તારણોઃ
- કોઈ પણ પૂર્ણાક 2k અથવા 2k + 1 સ્વરૂપનો હોય છે. જ્યાં, કોઈ પૂર્ણાક છે. 2k સ્વરૂપનો પૂર્ણક યુગ્મ પૂર્ણાક છે અને 2k + 1 સ્વરૂપનો પૂર્ણાક અયુગ્મ પૂર્ણાક છે.
- કોઈ પણ અયુગ્મ પૂર્ણાક 4k + 1 અથવા 4k + 3 સ્વરૂપનો હોય છે. જ્યાં, કોઈ પૂર્ણાક છે.
- 3 વડે વિભાજ્ય ન હોય તેવો પૂર્ણાક 3k+1 સ્વરૂપનો હોય છે. 5 વડે વિભાજ્ય ન હોય તેવો પૂર્ણાક 5k ± 1 અથવા 5k ± 2 સ્વરૂપનો હોય છે વગેરે. અહીં, દરેક કિસ્સામાં k એ કોઈ પૂર્ણાક છે.
→ અંકગણિતનું મૂળભૂત પ્રમેય
પ્રમેય (અંકગણિતનું મૂળભૂત પ્રમેય) ઃ દરેક વિભાજ્ય સંખ્યાને તેના અવયવોના ક્રમને અવગણીને અવિભાજ્ય સંખ્યાઓના ગુણાકાર તરીકે અનન્ય રીતે દર્શાવી શકાય છે.
→ અંકગણિતનું મૂળભૂત, પ્રમેય દર્શાવે છે કે, આપેલ કોઈ પણ વિભાજ્ય સંખ્યાનું તેના અવયવોના ક્રમને અવગણીને અવિભાજ્ય સંખ્યાઓના ગુણાકાર તરીકે અનન્ય રીતે નિરૂપણ કરી શકાય. આમ, 210નું અવિભાજ્ય અવયવોમાં અવયવીકરણ તરીકે 2 × 3 × 5 × 7 અથવા 7 × 5 × 3 × 2 અથવા 3 × 7 × 5 × 2 બધા જ એકસમાન છે.
→ આથી ઉપરોક્ત પ્રમેયને બીજા શબ્દોમાં આ રીતે પણ દર્શાવી શકાય કે, “1થી મોટી કોઈ પણ પ્રાકૃતિક સંખ્યાનું અવિભાજ્ય અવયવોમાં અવયવીકરણ તેમના ક્રમને અવગણીએ તો અનન્ય હોય છે.”
→ અવિભાજ્ય અવયવીકરણ કોઈ પણ વિભાજ્ય સંખ્યાને તેના
અવિભાજ્ય અવયવોના ગુણાકાર સ્વરૂપે દર્શાવવાની ક્રિયાને અવિભાજ્ય અવયવીકરણ કહે છે. જેમ કે, 27720 = 2 × 2 × 2 × 3 × 3 × 5 × 7 × 11
= 2 × 3 × 5 × 7 × 11
→ અવયવ વૃક્ષ: જ્યારે કોઈ વિભાજ્ય સંખ્યાનું અવિભાજ્ય અવયવીકરણ નીચે મુજબ કરવામાં આવે તેને અવયવ વૃક્ષ કહે છે.
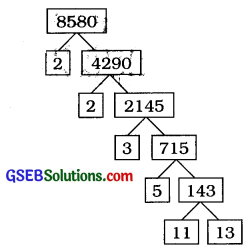
આથી 8580 = 2 × 2 × 3 x× 5 × 11 × 13
= 23 × 3 × 5 × 11 × 13
→ ગુ.સા.અ. બે કે તેથી વધુ આપેલી સંખ્યામાં રહેલા સામાન્ય અવિભાજ્ય અવયવના નાનામાં નાનાં ઘાતાંકવાળાં પદોના ગુણાકારને આપેલ સંખ્યાઓનો ગુ.સા.અ. (ગુરુતમ સામાન્ય અવયવ) કહે છે.
→ લ.સા.અ. બે કે તેથી વધુ આપેલી સંખ્યામાં રહેલા તમામ અવિભાજ્ય અવયવોના મહત્તમ ઘાતાંકવાળાં પદોના ગુણાકારને આપેલ સંખ્યાઓનો લ.સા.અ. (લઘુતમ સામાન્ય અવયવી) કહે છે.
→ કોઈ પણ બે ધન પૂર્ણાકો વ અને b માટે, ગુ.સા.અ. (a, b) × લ.સા.અ. (a, b) = a × b
આ પરિણામના ઉપયોગથી ચાર પૈકીની કોઈ પણ ત્રણ રાશિ આપેલ હોય તો ચોથી રાશિ સહેલાઈથી શોધી શકાય છે. ત્રણ ધન પૂર્ણાકો p, q અને જુના ગુ.સા.અ. અને લ.સા.અ. વચ્ચેનો સંબંધ ત્રણ ધન પૂર્ણાકો p, q અને r ના ગુ.સા.અ. અને લ.સા.અ. વચ્ચેનો સંબંધ નીચે મુજબનાં સમીકરણો દ્વારા મળે છે લ.સા.અ. (p, q, r)

→ જો વ અને b પરસ્પર અવિભાજ્ય સંખ્યાઓ હોય, તો ગુ.સા.અ. (a, b) = 1 અને લ.સા.અ. (a, b) = a × b.
→ બે કે તેથી વધુ આપેલ સંખ્યાઓનો ગુ.સા.અ. એ તેમના લ.સા.અ.નો અવયવ હોય જ છે. બીજા શબ્દોમાં, બે કે તેથી વધુ આપેલ સંખ્યાઓનો લ.સા.અ. એ તેમના ગુ.સા.અ.નો ગુણક હોય છે.
→ અસંમેય સંખ્યાઓનું પુનરાવર્તન : જ અસંમેય સંખ્યા જે સંખ્યાને પૂર્ણક p તથા શૂન્યતર પૂર્ણક q માટે 3 સ્વરૂપમાં લખી ન શકાય તે સંખ્યા sને અસંમેય સંખ્યા કહેવાય છે. આપણે √2 , √3, √7 , π, 0.10100100010000… જેવી અસંમેય સંખ્યાઓથી પરિચિત છીએ
→ આ વર્ષે આપણે અંકગણિતના મૂળભૂત પ્રમેયની મદદથી તે પૈકીની કેટલીક સંખ્યાઓ માટે તે સંખ્યાઓને અસંમેય સાબિત કરીશું.
→ જો p અવિભાજ્ય સંખ્યા હોય, તો √p અસંમેય સંખ્યા છે. કે જો કોઈ અવિભાજ્ય સંખ્યા p એ વ્રશ્નો અવયવ હોય, તો તે વનો પણ અવયવ હોય જ.
→ જો a સંમેય સંખ્યા હોય તથા Vb એ શૂન્યતર અસંમેય સંખ્યા હોય, તો a + √b , a – b, a = b તથા a – √b અસંમેય સંખ્યાઓ છે.
![]()
→ પ્રમેય : ધારો કે, p એ એક અવિભાજ્ય સંખ્યા છે. ધન પૂર્ણાક a માટે, વ એ p વડે વિભાજ્ય હોય, તો વ પણ p વડે વિભાજ્ય હોય. સાબિતી : ધારો કે, qનું અવિભાજ્ય અવયવોમાં અવયવીકરણ નીચે પ્રમાણે છે:
a = p1p2..pn, જ્યાં, p1, p2, pn એ અવિભાજ્ય સંખ્યાઓ છે. આવશ્યક નથી કે તે p1, p2,…, pn ભિન્ન સંખ્યાઓ જ હોય.
માટે a = (p1p2… pn) (p1p2…pn)
= p12p22……..pn2
હવે, આપણને આપેલ છે કે a એ p વડે વિભાજ્ય છે. માટે અંકગણિતના મૂળભૂત પ્રમેય પરથી કહી શકાય કે, Op એ gશ્નો એક અવિભાજ્ય અવયવ હોય. અંકગણિતના
મૂળભૂત પ્રમેયના અનન્યતા ભાગ પરથી કહી શકાય કે, વન્ના અવિભાજ્ય અવયવો માત્ર p1, p2 , pn છે. આથી ) એ p1, p2,.., pn પૈકીનો એક હોય. હવે, a = p1p2… pn હોવાથી p એ વનો પણ અવયવ છે.
→ પ્રમેય : √2 એ અસંમેય છે. સાબિતી : ધારો કે √2 સંમેય છે.
- આથી આપણે √2 = થાય તેવા પૂણકો 1 અને s (s ≠ 0) મેળવી શકીએ.
- જો ” અને sને 1 સિવાય સામાન્ય અવયવ હોય, તો સામાન્ય અવયવ વડે r તથા ને ભાગતાં √2 = \(\frac{a}{b}\) મળે.
- આપણે વ અને b પરસ્પર અવિભાજ્ય લઈ શકીએ. આથી b√2 = a
- આપણે બંને બાજ વર્ગ કરી પુન:ગોઠવણ કરીએ તો, 2b2 = a2 મળે. માટે a2 એ 3 વડે વિભાજ્ય છે. હવે, પ્રમેય 1.3 અનુસાર, a એ 2 વડે વિભાજ્ય છે.
- આથી આપણે કોઈ પૂર્ણાક c માટે a = 2c લખી શકીએ.
- aની કિંમત મૂકતાં આપણને 2b2 = 4c2 મળે. આથી b2 = 2c2 થાય.
- આનો અર્થ એ થાય કે, ‘એ 2 વડે વિભાજ્ય છે. આથી b પણ 2 વડે વિભાજ્ય છે. (ફરીથી પ્રમેય 1.3, p = 2 સાથે ઉપયોગમાં લેતાં) માટે વ તથા મને ઓછામાં ઓછો એક સામાન્ય અવયવ 2 છે.
- આથી વ અને મને 1 સિવાય કોઈ જ સામાન્ય અવયવ નથી તે ધારણાનો વિરોધાભાસ મળે.
- √2 સંમેય છે તે ધારણા અસત્ય હોવાથી આ વિરોધાભાસ ઉદ્ભવ્યો. આથી કહી શકાય કે, √2 અસંમેય છે.
→ સંમેય સંખ્યાઓ અને તેના દશાંશ નિરૂપણનું પુનરાવર્તન દરેક સંમેય સંખ્યાનું દશાંશ નિરૂપણ સાન્ત અથવા અનંત અને આવૃત્ત હોય છે.
→ જો x એ સાન્ત દશાંશ નિરૂપણવાળી સંમેય સંખ્યા હોય, તો ન્ને જ્યાં pઅને q પરસ્પર અવિભાજ્ય પૂર્ણાકો હોય અને qનું અવિભાજ્યમાં અવયવીકરણ 2n 5mળ સ્વરૂપમાં હોય તેવા સ્વરૂપમાં દર્શાવી શકાય. n, m એ અનૃણ પૂર્ણાકો છે. (જો m = n = 0, તો q = 1 તે અવિભાજ્યોમાં વર્ગીકરણ નથી. \(\frac{p}{q}\) પોતે જ પૂર્ણાક છે.) ઘ. ત., 0.35 = 60 = 20 =
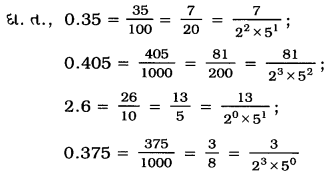
→ જો x = \(\frac{p}{q}\) માં qનું અવિભાજ્યોમાં અવયવીકરણ 25 સ્વરૂપે હોય અને n, m એ અનૃણ પૂર્ણાકો હોય, તો xનું દશાંશ નિરૂપણ સાન્ત હોય.

→ જો qનું અવિભાજ્યોમાં અવયવીકરણ અનુણ પૂણકો n, m માટે 2n 5m સ્વરૂપે ન હોય, તો x = \(\frac{p}{q}\) નું દશાંશ નિરૂપણ અનંત અને આવૃત્ત છે.
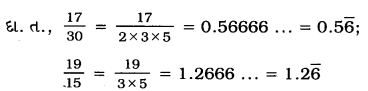
→ જો કોઈ સંમેય સંખ્યાનું દશાંશ નિરૂપણ અનંત અને આવૃત્ત હોય, તો તેના \(\frac{p}{q}\) સ્વરૂપમાં qનું અવિભાજ્યોમાં અવયવીકરણ 25ળ સ્વરૂપે ન હોય. જ્યાં, n અને m અનૃણ પૂર્ણાકો છે. કે
→ કોઈ પણ અસંમેય સંખ્યાનું દશાંશ નિરૂપણ અનંત અને અનાવૃત્ત હોય છે.
→ યુક્લિડનું ભાગાકારનું પૂર્વપ્રમેય આપેલ ધન પૂર્ણાકો a અને bને સંગત a = bq + r, 0 4 r ≤ bનું સમાધાન કરે તેવી પૂર્ણ સંખ્યાઓ q અને નું અસ્તિત્વ છે. (બંને સાથે શૂન્ય નહીં)
→ યુક્લિડની ભાગપ્રવિધિઃ યુક્લિડના ભાગાકારના પૂર્વપ્રમેય અનુસાર a > b હોય તેવા કોઈ પણ બે ધન પૂર્ણાકો વ અને મનો ગુ.સા.અ. નીચે પ્રમાણે મેળવી શકાય?
સોપાન 1: a = bq + , 0 < r < b થાય તેવા 9 અને મેળવવા ભાગાકારના પૂર્વપ્રમેયનો ઉપયોગ કરો.
સોપાન 2: જો n = 0 નો ગુ.સા.અ. b છે. જો r ≠ 0 તો ભાગાકારના પૂર્વપ્રમેયનો છે અને માટે ઉપયોગ કરો.
સોપાન ૩: જ્યાં સુધી શેષ ૦ ન મળે ત્યાં સુધી આ પ્રક્રિયા ચાલુ રાખો. શેષ ૦ થાય તે તબક્કે ભાગફળ એ ગુ.સા.અ. (a, b) થાય. વળી, ગુ.સા.અ. (a, b) = ગુ.સા.અ.
(b, r) અંકગણિતનું મૂળભૂત પ્રમેયઃ દરેક વિભાજ્ય સંખ્યાને તેના અવયવોના ક્રમને અવગણીને અવિભાજ્ય સંખ્યાઓના ગુણાકાર તરીકે અનન્ય રીતે દર્શાવી શકાય છે.
→ જો p અવિભાજ્ય હોય અને d એ p વડે વિભાજ્ય હોય, તો વ પણ રૂ વડે વિભાજ્ય છે.
→ કોઈ પણ અવિભાજ્ય પૂર્ણાકનું વર્ગમૂળ એ અસંમેય સંખ્યા છે. ∠2, ∠3, ∠5 વગેરે અસંમેય સંખ્યાઓ છે.
→ કોઈ પણ સંમેય સંખ્યા અને અસંમેય સંખ્યાનો સરવાળો તથા તફાવત અસંમેય સંખ્યા છે.
→ શૂન્યતર હોય તેવી કોઈ પણ સંમેય સંખ્યા અને અસંમેય સંખ્યાનો ગુણાકાર તથા ભાગાકાર અસંમેય સંખ્યા છે.
→ કોઈ પણ બે ધન પૂર્ણાકો વ અને b માટે,
ગુ.સા.અ. (a, b) × લ.સા.અ. (a, b) = a × b
→ કોઈ પણ ત્રણ ધન પૂણકો a, b અને તે માટે, લ.સા.અ. (a, b, c)

→ કોઈ પણ બે ધન પૂર્ણાકો વ અને b માટે, ગુ.સા.અ. (ka, kb) = k ગુ.સા.અ. (a, b) જ્યાં, k શૂન્યતર અચળાંક છે.
→ જેનું દશાંશ નિરૂપણ સાન્ત છે તેવી સંમેય સંખ્યા વને આપણે \(\frac{p}{q}\) સ્વરૂપમાં દર્શાવી શકીએ. p અને q પરસ્પર અવિભાજ્ય છે અને અનૃણ પૂર્ણાકો n, m માટે qનું અવિભાજ્યોમાં અવયવીકરણ 2n5m સ્વરૂપમાં હોય.
→ જેમાં અનૃણ પૂર્ણાકો n, m માટે qનું અવિભાજ્યોમાં અવયવીકરણ 25ળ સ્વરૂપનું હોય તેવી સંમેય સંખ્યા x = \(\frac{p}{q}\) નું દશાંશ નિરૂપણ સાન્ત હોય.
→ જેમાં અનૃણ પૂર્ણાકોn, m માટે qનું અવિભાજ્યોમાં અવયવીકરણ 2n5m સ્વરૂપનું ન હોય તેવી સંમેય સંખ્યા x = \(\frac{p}{q}\)નું દશાંશ નિરૂપણ અનંત અને આવૃત્ત હોય.