GSEB Class 10 Science Important Questions Chapter 10 પ્રકાશ-પરાવર્તન અને વક્રીભવન

Gujarat Board GSEB Class 10 Science Important Questions Chapter 10 પ્રકાશ-પરાવર્તન અને વક્રીભવન Important Questions and Answers.

GSEB Class 10 Science Important Questions Chapter 10 પ્રકાશ-પરાવર્તન અને વક્રીભવન

વિશેષ પ્રોત્તર

પ્રશ્ન 1.
નીચેના દાખલા ગણોઃ

પ્રશ્ન 1.
0.3m કેન્દ્રલંબાઈવાળા બહિર્ગોળ અરીસાની સામે 20 cm અંતરે વસ્તુ મૂકેલી છે. અરીસા વડે મળતા પ્રતિબિંબનું સ્થાન, પ્રકાર અને મોટવણી શોધો.
જવાબ:
U = 12 cm, આભાસી અને ચતું, m = 0.6

પ્રશ્ન 2.
અંતર્ગોળ અરીસાની વક્રતાત્રિજ્યા 12 cm છે. તેના દ્વારા મળતું પ્રતિબિંબ વાસ્તવિક અને \(\frac{3}{2}\) મોટવણીવાળું મળે છે. વસ્તુ-અંતર અને પ્રતિબિંબ-અંતર શોધો.
જવાબ:
u = – 10 cm, v = – 15 cm

પ્રશ્ન 3.
બસમાં સાઈડ ગ્લાસ તરીકે લગાડેલ બહિર્ગોળ અરીસાની વક્રતાત્રિજ્યા 3m છે. બસની પાછળ અરીસાથી 6m અંતરે ઊભેલી કારના પ્રતિબિંબનું સ્થાન, પ્રકાર અને પરિમાણ જણાવો.
જવાબ:
D = 1.2 m, આભાસી અને ચતું, m = 0.2

પ્રશ્ન 4.
અંતર્ગોળ અરીસાથી 32 cm દૂર, 2 cm ઊંચાઈવાળી વસ્તુ મૂકેલી છે. અરીસાથી મળતું પ્રતિબિંબ વાસ્તવિક, ઊલટું અને 1.5 ગણું મોટું મળે છે, તો અંતર્ગોળ અરીસાની કેન્દ્રલંબાઈ અને પ્રતિબિંબ-અંતર શોધો.
જવાબ:
f = 19.2 cm, v = -48 cm

પ્રશ્ન 5.
કાચની સાપેક્ષમાં હીરાનો વક્રીભવનાંક 1.61 છે. કાચનો વક્રીભવનાંક 1.5 હોય, તો હીરાનો નિરપેક્ષ વક્રીભવનાંક શોધો.
જવાબ:
n = 2.415

પ્રશ્ન 6.
બરફનો નિરપેક્ષ વક્રીભવનાંક 1.31 છે. શૂન્યાવકાશમાં પ્રકાશનો વેગ ૩× 10⁸ ms^-1 હોય, તો બરફમાં પ્રકાશનો વેગ શોધો.
જવાબ:
U = 2.29 × 10⁸ m s^-1

પ્રશ્ન 7.
1.5 વક્રીભવનાંકવાળા કાચમાં પ્રકાશનો વેગ 2 × 10⁸ ms^-1 છે. કોઈ એક પ્રવાહીમાં પ્રકાશનો વેગ 2.5 × 10⁸ ms^-1છે. પ્રવાહીનો નિરપેક્ષ વક્રીભવનાંક શોધો.
જવાબ:
n₁ = 1.2

પ્રશ્ન 8.
\(\sqrt{2}\) વક્રીભવનાંકવાળા કાચના લંબઘનમાં 45°ના કોણે આપાત કરેલું પ્રકાશનું કિરણ લંબઘનમાંથી હવામાં પ્રવેશે છે, તો હવામાં વક્રીભૂતકોણ શોધો. હવાનો વક્રીભવનાંક 1 લો.
જવાબ:
r = 30°

પ્રશ્ન 9.
પ્રકાશનું કિરણ હવામાંથી 1.50 વક્રીભવનાંક ધરાવતા કાચના માધ્યમમાં દાખલ થાય છે. કાચના માધ્યમમાં પ્રકાશનો વેગ કેટલો હશે?
જવાબ:
D = 2.0 × 10⁸ m s^-1

પ્રશ્ન 10.
લેન્સની આગળ 60 cm દૂર મૂકેલી વસ્તુનું પ્રતિબિંબ આભાસી અને લેન્સના આગળના ભાગમાં 20 cm અંતરે મળે છે. આ લેન્સની કેન્દ્રલંબાઈ ગણો. લેન્સનો પ્રકાર જણાવો.
જવાબ:
f = -30 cm, અંતર્ગોળ લેન્સ

પ્રશ્ન 11.
એક લેન્સની કેન્દ્રલંબાઈ -25 cm છે. આ લેન્સનો પાવર અને પ્રકાર જણાવો.
જવાબ:
P = -4D, અંતગોંળ લેન્સ

પ્રશ્ન 12.
એક લેન્સનો પાવર +5D છે. તે લેન્સની કેન્દ્રલંબાઈ કરતાં બમણાં અંતરે વસ્તુ મૂકવામાં આવે છે, તો

1. લેન્સની કેન્દ્રલંબાઈ શોધો.
2. લેન્સથી મળતા પ્રતિબિંબનું સ્થાન જણાવો.

જવાબ:

1. f = 20 cm
2. વસ્તુની વિરુદ્ધ બાજુએ 40 cm અંતરે

પ્રશ્ન 13.
બહિર્ગોળ લેન્સની કેન્દ્રલંબાઈ 25 cm છે. આ લેન્સથી વસ્તુનું પ્રતિબિંબ લેન્સની બીજી બાજુ 75 cm અંતરે મળે છે, તો તે આ વસ્તુનું સ્થાન શોધો. પ્રતિબિંબનો પ્રકાર જણાવો.
જવાબ:
u = -37.5 cm;
વાસ્તવિક, ઊલટું અને વસ્તુ કરતાં મોટું

પ્રશ્ન 14.
એક લેન્સનો પાવર – 4D છે. આ લેન્સથી પ્રતિબિંબ આભાસી, સીધું અને 5 cm અંતરે મળે છે, તો વસ્તુનું સ્થાન શોધો.
જવાબ:
u =- 6.25 cm

પ્રશ્ન 15.
પ્રકાશનું કિરણ શૂન્યાવકાશમાં 100 m અંતર જેટલા સમયમાં કાપે છે, તેટલા જ સમયમાં 1.5 વક્રીભવનાંક ધરાવતા કાચમાં કેટલું અંતર કાપશે?
જવાબ:
66.67 m

પ્રશ્ન 16.
એક અંતર્ગોળ અરીસાની કેન્દ્રલંબાઈ 20 cm છે. તેના ધ્રુવથી 25 cm અંતરે રહેલી વસ્તુ માટે પ્રતિબિંબનું અંતર અને પ્રકાર શોધો.
જવાબ:
100 cm; વાસ્તવિક, ઊલટું અને મોટું

પ્રશ્ન 17.
3 cm કેન્દ્રલંબાઈવાળો એક બહિર્ગોળ અરીસો વાહનમાં લગાડેલો છે. જો તેનાથી 5 m પાછળ એક વાહન ઊભું હોય, તો પ્રતિબિંબનું સ્થાન અને તેનો પ્રકાર જણાવો.
જવાબ:
v = 1.875 m (અરીસાની પાછળ); આભાસી, ચતું

પ્રશ્ન 18.
5 cm ઊંચાઈની વસ્તુને 15 cm કેન્દ્રલંબાઈ ધરાવતા બહિર્ગોળ અરીસાની સામે 10 cm અંતરે મૂકેલી છે. પ્રતિબિંબનું સ્થાન, પ્રકાર અને કદ શોધો.
જવાબ:
v = 6 cm (અરીસાની પાછળ; આભાસી, ચતું, 3 cm ઊંચાઈનું)

પ્રશ્ન 19.
એક અંતર્ગોળ અરીસા પર તેની મુખ્ય અક્ષને સમાંતર એવા સૂર્યનાં કિરણો આપાત થાય છે. સૂર્યનું પ્રતિબિંબ અરીસાના ધ્રુવથી 12 cm અંતરે મળતું હોય, તો તેની વક્રતાત્રિજ્યા શોધો.
જવાબ:
24 cm

પ્રશ્ન 20.
અંતર્ગોળ અરીસાથી 12 cm અંતરે એક વસ્તુ મૂકતાં, તેનું ઊલટું પ્રતિબિંબ રચાય છે. પ્રતિબિંબની ઊંચાઈ વસ્તુ કરતાં બમણી છે, તો તે ક્યાં રચાયું હશે?
જવાબ:
અરીસાની આગળના ભાગમાં 24 cm અંતરે

પ્રશ્ન 21.
અંતર્ગોળ અરીસાથી 10 cm અંતરે એક વસ્તુ મૂકતાં, તેનું ચતું પ્રતિબિંબ રચાય છે. પ્રતિબિંબની ઊંચાઈ વસ્તુ કરતાં બમણી છે, તો તે ક્યાં રચાયું હશે?
જવાબ:
અરીસાની પાછળના ભાગમાં 20 cm અંતરે

પ્રશ્ન 22.
ઊંચાઈની વસ્તુને લેન્સથી 60 cm અંતરે મૂકેલી છે, તો પ્રતિબિંબની ઊંચાઈ શોધો.
જવાબ:
પ્રતિબિંબનું કદ/ઊંચાઈ = 1.0 cm

પ્રશ્ન 23.
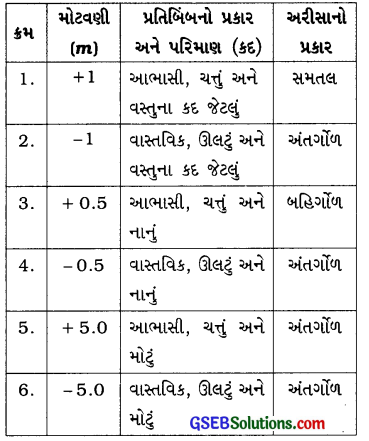
પ્રતિબિંબની મોટવણીનાં મૂલ્યો + 1, -1, + 0.5, -0.5, + 5.0 અને 75.0 પરથી અરીસા વડે રચાતાં પ્રતિબિંબના પ્રકાર, કદ તેમજ અરીસાનો પ્રકાર નક્કી કરો.
જવાબ:

પ્રશ્ન 24.
4 cm ઊંચાઈવાળી વસ્તુને 12 cm કેન્દ્રલંબાઈ ધરાવતા અંતર્ગોળ અરીસાની સામે 18 cm અંતરે મૂકવામાં આવે છે, તો પ્રતિબિંબનું સ્થાન, પ્રકાર અને ઊંચાઈ શોધો.
જવાબ:
v = -36 cm (વસ્તુ તરફ) વક્રતાકેન્દ્રથી દૂર, વાસ્તવિક, ઊલટું અને 8 cm ઊંચાઈનું પ્રતિબિંબ મળે.

પ્રશ્ન 25.
બહિર્ગોળ લેન્સ વડે વસ્તુનું લેન્સથી 40 cm દૂર વાસ્તવિક અને ઊલટું પ્રતિબિંબ રચાય છે. જો પ્રતિબિંબનું કદ વસ્તુના કદ જેટલું જ હોય, તો વસ્તુ-અંતર શોધો. બહિર્ગોળ લેન્સનો પાવર શોધો.
જવાબ:
u = -40 cm; પાવર P = + 5.0 D.

પ્રશ્ન 26.
પ્રકાશ પાણીમાંથી કાચમાં પ્રવેશે ત્યારે તેનો વક્રીભવનાંક 1.12 છે. જો કાચનો નિરપેક્ષ વક્રીભવનાંક 1.5 હોય, તો પાણીનો નિરપેક્ષ વક્રીભવનાંક શોધો.
જવાબ:
n_w = 1.34

પ્રશ્ન 27.
પ્રકાશ કાચમાંથી પાણીમાં પ્રવેશે ત્યારે કાચની સાપેક્ષમાં પાણીનો વક્રીભવનાંક 0.9 છે. બે માધ્યમોને છૂટી પાડતી સપાટી આગળ આપાતકોણનું મૂલ્ય 26°30′ હોય, તો સપાટી આગળ વક્રીભવનકોણનું મૂલ્ય શોધો. sin26°30′ = 0.45 (અંદાજિત) લો.
જવાબ:
30°

પ્રશ્ન 28.
30 cm કેન્દ્રલંબાઈવાળા અંતર્ગોળ લેન્સની સામે મુખ્ય અક્ષ પર છે વસ્તુને લંબરૂપે મૂકેલી છે. જો વસ્તુ લેન્સથી 20 cm અંતરે હોય, હું તો પ્રતિબિંબનું સ્થાન શોધો.
જવાબ:
v = -12 cm (વસ્તુ તરફ)

પ્રશ્ન 29.
બહિર્ગોળ લેન્સનો પાવર +4.0D છે. વસ્તુને લેન્સથી કેટલા , અંતરે મૂકીએ તો તેનું વાસ્તવિક, ઊલટું અને વસ્તુ જેટલા જ કદનું પડદા પર પ્રતિબિંબ મળે?
જવાબ:
u = -50 cm

પ્રશ્ન 2.
તફાવતના મુદ્દા લખો:

પ્રશ્ન 1.
અંતર્ગોળ અરીસો અને બહિર્ગોળ અરીસો
ઉત્તર:

પ્રશ્ન 2.
વાસ્તવિક પ્રતિબિંબ અને આભાસી પ્રતિબિંબ
ઉત્તર:

પ્રશ્ન ૩.
બહિર્ગોળ લેન્સ અને અંતર્ગોળ લેન્સ
ઉત્તર:

પ્રશ્ન 3.
નીચેના વિધાનોનાં વૈજ્ઞાનિક કારણો આપોઃ

પ્રશ્ન 1.
વાહનની હેડલાઇટમાં, ટૉર્ચમાં અને સર્ચલાઈટમાં (નાના દર્પણમુખવાળો) અંતર્ગોળ અરીસો વપરાય છે.
ઉત્તર:
વાહનની હેડલાઇટમાં, ટૉર્ચમાં અને સર્ચલાઈટમાં પ્રકાશઉદ્ગમને અંતર્ગોળ અરીસાના મુખ્ય કેન્દ્ર પર ગોઠવવામાં આવે છે. પરિણામે પ્રકાશ-ઉદ્ગમમાંથી નીકળતાં પ્રકાશનાં કિરણો અંતર્ગોળ અરીસા વડે પરાવર્તન પામી, સમાંતર કિરણજૂથરૂપે દૂર સુધી ફેલાય છે. તેથી દૂર સુધીનો માર્ગ પ્રકાશિત દેખાય છે.

પ્રશ્ન 2.
વાહનોના સાઈડ ગ્લાસ બહિર્ગોળ અરીસાના બનેલા હોય છે.
ઉત્તર:
બહિર્ગોળ અરીસાની સામે વસ્તુ ગમે તેટલા અંતરે હોય તોપણ પ્રતિબિંબ આભાસી, ચતું, નાનું અને અરીસામાં જોવા મળે છે. પ્રતિબિંબ અરીસામાં ધ્રુવ અને મુખ્ય કેન્દ્ર આગળ રચાતું હોવાથી વાહનચાલકને નજીકમાં સ્પષ્ટ પ્રતિબિંબ દેખાય છે. બહિર્ગોળ અરીસાનો દષ્ટિ-વિસ્તાર ખૂબ મોટો છે. આથી વાહનચાલક બહિર્ગોળ અરીસા વડે પાછળના વાહનવ્યવહારને આવરી લેતું દશ્ય જોઈ શકે છે અને સુરક્ષિત રીતે પોતાના વાહનને ચલાવી શકે છે. તેથી વાહનોને સાઇડ ગ્લાસ બહિર્ગોળ અરીસાના બનેલા હોય છે.

પ્રશ્ન 3.
સૌર-ભટ્ટી અને સોલર કૂકરમાં મોટો અંતર્ગોળ અરીસો વાપરવામાં આવે છે.
ઉત્તર:
સૂર્યનાં સમાંતર કિરણો સૌર-ભટ્ટી અને સોલર કૂકરમાં ગોઠવેલા મોટા અંતગોળ અરીસા પર આપાત થઈ પરાવર્તન પામે છે. આ પરાવર્તિતકિરણો અંતર્ગોળ અરીસાના મુખ્ય કેન્દ્ર આગળ કેન્દ્રિત થાય છે. અંતર્ગોળ અરીસો મોટો હોવાથી તેના મુખ્ય કેન્દ્ર આગળ વધુ જથ્થામાં કિરણો કેન્દ્રિત થઈ વધુ પ્રમાણમાં ઉષ્મા-ઊર્જા ઉત્પન્ન કરે છે. આ ઉષ્મા-ઊર્જા સૌર-ભઠ્ઠીમાં ઊંચું તાપમાન મેળવવા કે સોલર કૂકરમાં ખોરાક રાંધવા માટે ઉપયોગમાં લેવાય છે.

પ્રશ્ન 4.
દાઢી કરવા કે મેક-અપ કરવા માટે અંતર્ગોળ અરીસો વાપરવામાં આવે છે.
ઉત્તર:
જો ચહેરો અંતર્ગોળ અરીસાના ધ્રુવ અને મુખ્ય કેન્દ્રની વચ્ચે રાખવામાં આવે, તો ચહેરાનું આભાસી, ચતું અને મોટું પ્રતિબિંબ મળે છે. અંતર્ગોળ અરીસામાં ચહેરાનું મોટું પ્રતિબિંબ દેખાતું હોવાથી દાઢી કરવામાં કે મૅક-અપ કરવામાં સરળતા રહે છે.

પ્રશ્ન 5.
નદીમાં તરતી માછલીને વીંધવી મુશ્કેલ છે.
ઉત્તર:
નદીમાં તરતી માછલી પરથી આવતાં પ્રકાશનાં કિરણો પાણીના ઘટ્ટ માધ્યમમાંથી હવાના પાતળા માધ્યમમાં પ્રવેશે છે, ત્યારે તેમનું વક્રીભવન થઈ લંબથી દૂર જાય છે. પરિણામે અવલોકનકતને માછલી તેના મૂળ સ્થાનથી ઊંચે દેખાય છે. આમ, અવલોકનકર્તા માછલીનું સાચું સ્થાન નક્કી ન કરી શકતો હોવાથી નદીમાં તરતી માછલીને વીંધવી મુશ્કેલ છે.

પ્રશ્ન 6.
ઘડિયાળ રિપેર કરનાર બહિર્ગોળ લેન્સનો ઉપયોગ કરે છે.
ઉત્તરઃ
બહિર્ગોળ લેન્સના પ્રકાશીય કેન્દ્ર ‘O’ અને મુખ્ય કેન્દ્ર ‘F’ વચ્ચે વસ્તુ મૂકતાં વસ્તુનું આભાસી, ચતું અને મોટું પ્રતિબિંબ લેન્સની વસ્તુ તરફની બાજુએ 2Fથી દૂર મળે છે. ઘડિયાળ રિપેર કરનાર ઘડિયાળના સૂક્ષ્મ ભાગોને લેન્સ અને મુખ્ય કેન્દ્રની વચ્ચે રાખીને જોતાં તે મોટા દેખાય છે. તેથી તેને રિપેરિંગમાં સરળતા રહે છે.

પ્રશ્નોત્તર

પ્રસ્તાવના

પ્રશ્ન 1.
પ્રકાશ એટલે શું? તેનું સ્વરૂપ જણાવો.
ઉત્તર:
આંખમાં સંવેદના ઉપજાવતાં વિદ્યુતચુંબકીય વિકિરણને પ્રકાશ કહે છે.

• સામાન્ય રીતે, પ્રકાશ તરંગ સ્વરૂપ ધરાવે છે.
  [નોંધઃ કેટલાક સંજોગોમાં પ્રકાશ કણોના પ્રવાહ સ્વરૂપે પણ હું વર્તે છે.]

પ્રશ્ન 2.
વસ્તુ શાથી દેખાય છે?
ઉત્તર:
વસ્તુ તેની પર પડતા પ્રકાશનું પરાવર્તિત કરે છે. આ પરાવર્તિત પ્રકાશ જ્યારે આપણી આંખો દ્વારા ગ્રહણ થાય ત્યારે આપણને તે વસ્તુ દેખાય છે.

પ્રશ્ન 3.
પ્રકાશના મૂળભૂત ગુણધર્મો લખો અને સમજાવો.
ઉત્તર:

1. પ્રકાશ એ ઊર્જાનું એક સ્વરૂપ છે, જે તરંગ સ્વરૂપે ગતિ કરે છે.
2. વિદ્યુતચુંબકીય તરંગો તરીકે ઓળખાતા પ્રકાશના તરંગોને પ્રસરવા દ્રવ્ય માધ્યમની જરૂર હોતી નથી. તેથી તેમને બિનયાંત્રિક તરંગો કહે છે.
3. પ્રકાશની શૂન્યાવકાશમાં ઝડપ આશરે 3 × 10⁸ ms^-1 છે.
4. જ્યારે પ્રકાશ પારદર્શક માધ્યમમાં ગતિ કરે છે ત્યારે તેની ઝડપમાં ઘટાડો થાય છે. ઝડપમાં થતો ઘટાડો માધ્યમના પ્રકાર પર આધાર રાખે છે.
5. દશ્યપ્રકાશની તરંગલંબાઈ 4 × 10^-7 m(4000 A)થી 8 × 10^-7m (8000 Á) સુધીની છે.
6. સામાન્ય પદાર્થના કદની સરખામણીમાં દશ્યપ્રકાશની તરંગલંબાઈનું મૂલ્ય ઘણું નાનું છે. આ પરિસ્થિતિમાં પ્રકાશના તરંગો એક બિંદુથી બીજા બિંદુને જોડતા સુરેખ પથ પર ગતિ કરે છે તેમ કલ્પી શકાય.
   • પ્રકાશના પ્રસરણની દિશામાં એક બિંદુથી બીજા બિંદુને
     જોડતા પ્રકાશના સુરેખ પથને પ્રકાશનું કિરણ કહે છે. પ્રકાશનાં કિરણોના સમૂહને પ્રકાશનું કિરણપુંજ કહે છે.
7. 
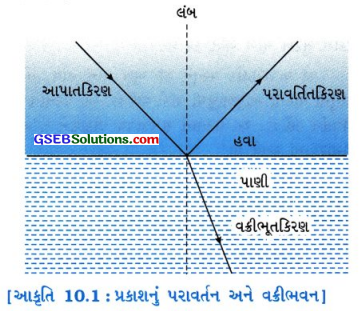
   આકૃતિ 10.1માં દર્શાવ્યા મુજબ જ્યારે પ્રકાશનું કિરણ બે માધ્યમો(દા. ત., હવા અને પાણી)ને છૂટી પાડતી સપાટી પર આપાત થાય છે ત્યારે સામાન્ય રીતે તેનું આંશિક પરાવર્તન અને વક્રીભવન થાય છે.
8. સંપૂર્ણ પૉલિશ કરેલી ચળકતી સમતલ સપાટી પર આપાત થતા પ્રકાશનું વધુ પ્રમાણમાં પરાવર્તન થાય છે, જ્યારે પારદર્શક માધ્યમ પર આપાત થતા પ્રકાશનું મુખ્યત્વે વક્રીભવન થાય છે.
9. ગોલીય (અથવા પરવલયાકાર) અરીસા અને લેન્સ દ્વારા પ્રકાશના કિરણોને કેન્દ્રિત અથવા વિકેન્દ્રિત કરી શકાય છે.

પ્રશ્ન 4.
પ્રકાશનું પરાવર્તન એટલે શું? તેના પ્રકારો જણાવો.
ઉત્તર:
“કોઈ વસ્તુ પર પ્રકાશ આપાત કરતાં વસ્તુની સપાટી – પરથી પ્રકાશની પાછા વળવાની ઘટનાને પ્રકાશનું પરાવર્તન કહે છે.”
પ્રકાશના પરાવર્તનના બે પ્રકારો છેઃ

1. નિયમિત પરાવર્તન અને
2. અનિયમિત (અથવા ડિફયુસ) પરાવર્તન.

પ્રશ્ન 5.
પ્રકાશનું નિયમિત અને અનિયમિત પરાવર્તન કોને કહે છે?
ઉત્તર:
પ્રકાશનું નિયમિત પરાવર્તન : જ્યારે પ્રકાશનું સમાંતર કિરણપુંજ ચળકતી, સમતલ, લીસી સપાટી પર આપાત થાય છે ત્યારે પરાવર્તિત પ્રકાશનું કિરણપુંજ ચોક્કસ દિશામાં સમાંતર રહે છે. પ્રકાશના આ પ્રકારના પરાવર્તનને નિયમિત પરાવર્તન કહે છે. (જુઓ આકૃતિ 10.5)

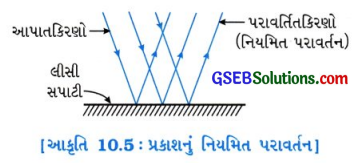
ઉદાહરણ સમતલ અરીસા વડે થતું પ્રકાશનું પરાવર્તન.

પ્રકાશનું અનિયમિત પરાવર્તનઃ જ્યારે પ્રકાશનું સમાંતર કિરણપુંજ અનિયમિત કે ખરબચડી સપાટી પર આપાત થાય છે ત્યારે પરાવર્તિત પ્રકાશનું કિરણપુંજ સમાંતર રહેતું નથી. પરંતુ સમગ્ર વિસ્તારમાં ફેલાય છે. પ્રકાશના આ પ્રકારના પરાવર્તનને અનિયમિત પરાવર્તન કહે છે. (જુઓ આકૃતિ 10.6)

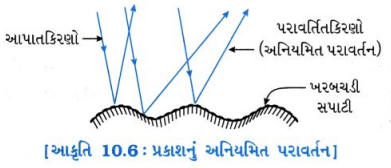
ઉદાહરણ પુસ્તક, ખુરશી, ટેબલ વગેરે વડે થતું પ્રકાશનું પરાવર્તન.

પ્રશ્ન 6.
પ્રકાશના પરાવર્તનના કિસ્સામાં આપાતકોણ અને પરાવર્તનકોણની વ્યાખ્યાઓ લખો.
ઉત્તર:

1. આપાતકોણ (i) આપાતકિરણે, આપાતબિંદુએ સપાટીને દોરેલ લંબ સાથે બનાવેલ કોણને આપાતકોણ (i) કહે છે.
2. પરાવર્તનકોણ (r) : પરાવર્તિતકિરણે, આપાતબિંદુએ સપાટીને દોરેલ લંબ સાથે બનાવેલ કોણને પરાવર્તનકોણ (r) કહે છે.
   

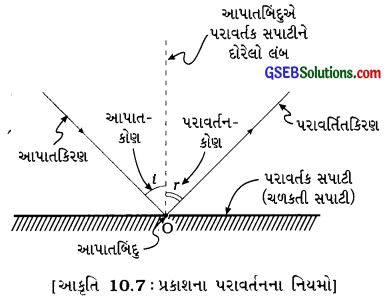
પ્રશ્ન 7.
પ્રકાશના પરાવર્તનના નિયમો લખો.
ઉત્તર:
પ્રકાશના પરાવર્તનના નિયમો નીચે મુજબ છે:

1. આપાતકોણ (i) અને પરાવર્તનકોણ (r) સમાન હોય છે, એટલે કે i = r.
2. આપાતકિરણ, અરીસાના આપાતબિંદુએ સપાટી પર દોરેલ લંબ અને પરાવર્તિતકિરણ બધાં એક જ સમતલમાં હોય છે.

ખાસ નોંધ:

1. પ્રકાશના પરાવર્તનના નિયમો ગોલીય સપાટી સહિત બધા પ્રકારની પરાવર્તક સપાટીને લાગુ પડે છે.
2. આ નિયમો નિયમિત તેમજ અનિયમિત પરાવર્તન બંનેને લાગુ પડે છે.
3. પ્રકાશનું કિરણ અરીસા પર લંબરૂપે આપાત થતું હોય ત્યારે તે જ માર્ગે પાછું પરાવર્તિત થાય છે. એટલે કે i = r = 0.
4. ચાંદી પ્રકાશનું ઉત્તમ પરાવર્તક ગણાય છે.

પ્રશ્ન 8.
વસ્તુનું પ્રતિબિંબ રચાયું છે તેમ ક્યારે કહેવાય? પ્રતિબિંબના પ્રકાર વિશે સ્પષ્ટતા કરો.
ઉત્તર:
વસ્તુ પરના કોઈ એક બિંદુએથી શરૂ કરી ઘણાં બધાં કિરણો પરાવર્તન અથવા વક્રીભવન પામી, બીજા કોઈ એક બિંદુએ મળે અથવા મળતાં હોય તેવો ભાસ થાય, તો બીજા બિંદુને પ્રથમ બિંદુનું પ્રતિબિંબ કહેવાય.
પ્રતિબિંબના બે પ્રકાર છે :

(1) વાસ્તવિક પ્રતિબિંબ અને
(2) આભાસી પ્રતિબિંબ.

(1) વાસ્તવિક પ્રતિબિંબ: જો પ્રકાશનાં કિરણો પરાવર્તન કે વક્રીભવન પામી, વાસ્તવમાં કોઈ એક બિંદુએ મળતાં હોય, તો તેમનાં વડે રચાતા પ્રતિબિંબને વાસ્તવિક પ્રતિબિંબ કહે છે.

• વાસ્તવિક પ્રતિબિંબ પડદા પર ઝીલી શકાય છે.
• વાસ્તવિક પ્રતિબિંબ હંમેશાં ઊંધું હોય છે.

(2) આભાસી પ્રતિબિંબ: જો પ્રકાશનાં કિરણો પરાવર્તન કે વક્રીભવન પામી, વાસ્તવમાં મળતાં ન હોય, પરંતુ મળતાં હોય તેવો ભાસ થતો હોય, તો તેમનાં વડે રચાતા પ્રતિબિંબને આભાસી પ્રતિબિંબ કહે છે.

• આભાસી પ્રતિબિંબ પડદા પર ઝીલી શકાતું નથી.
• આભાસી પ્રતિબિંબ હંમેશાં ચતું હોય છે.

પ્રશ્ન 9.
અરીસો કોને કહે છે? તેના પ્રકાર જણાવો.
ઉત્તર:
લીસી અને ચળકતી સપાટી જે તેના પર પડતા લગભગ બધા પ્રકાશનું પરાવર્તન કરે છે, તેને અરીસો કહે છે.
અરીસાના બે પ્રકાર છે :

1. સમતલ અરીસો અને
2. ગોલીય અરીસો.

પ્રશ્ન 10.
સમતલ અરીસો એટલે શું? સમતલ અરીસા વડે રચાતા પ્રતિબિંબની ખાસિયતો જણાવો.
ઉત્તર:
જો અરીસાની પરાવર્તક સપાટી સમતલ (સપાટ) હોય, તો તે અરીસાને સમતલ અરીસો કહે છે.

સમતલ અરીસા વડે રચાતા પ્રતિબિંબની ખાસિયતો નીચે મુજબ છેઃ

1. સમતલ અરીસા વડે રચાતું પ્રતિબિંબ હંમેશાં આભાસી અને ચતું હોય છે.
2. પ્રતિબિંબનું પરિમાણ (Size) વસ્તુના પરિમાણ જેટલું જ હોય છે.
3. વસ્તુ અરીસાથી જેટલા અંતરે આગળ હોય છે, તેટલા જ અંતરે વસ્તુનું પ્રતિબિંબ અરીસાના પાછળના ભાગમાં રચાય છે.
4. વસ્તુના પ્રતિબિંબમાં બાજુઓ ઊલટાયેલી હોય છે. એટલે કે વસ્તુની ડાબી બાજુ પ્રતિબિંબની જમણી બાજુ તરીકે અને વસ્તુની જમણી બાજુ પ્રતિબિંબની ડાબી બાજુ તરીકે દેખાય છે.

પ્રશ્ન 11.
સમતલ અરીસાના ઉપયોગો જણાવો.
ઉત્તરઃ

1. સમતલ અરીસો દર્પણ તરીકે વપરાય છે.
2. સમતલ અરીસા પેરિસ્કોપ અને કેલિડોસ્કોપ બનાવવા વપરાય છે.

પ્રશ્ન 12.
ગોલીય અરીસો કોને કહે છે? તેના પ્રકાર જણાવો.
ઉત્તર:
જે અરીસાની પરાવર્તક સપાટી પોલા ગોળાના પૃષ્ઠનો એક ભાગ હોય તેને ગોલીય અરીસો કહે છે. અરીસાની એક બાજુ સંપૂર્ણ પૉલિશ કરેલી અને પરાવર્તક હોય છે, જ્યારે બીજી બાજુ અપારદર્શક હોય છે. ગોલીય અરીસાની પરાવર્તક સપાટી અંદરની તરફ કે બહારની તરફ વક્રાકાર હોય છે.
ગોલીય અરીસાના બે પ્રકાર છેઃ
(1) અંતર્ગોળ અરીસો અને
(2) બહિર્ગોળ અરીસો.

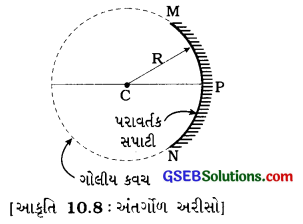
(1) અંતર્ગોળ અરીસો જે ગોલીય અરીસાની પરાવર્તક સપાટી અંદરની તરફ વક્રાકાર હોય, તેને અંતર્ગોળ અરીસો કહે છે.
મુખ્ય અક્ષને સમાંતર કિરણપુંજ આ અરીસા વડે પરાવર્તન પામી, એક બિંદુએ કેન્દ્રિત થાય છે. તેથી તેને અભિસારી અરીસો કહે છે.
દા. ત., ચકચકિત ચમચીની અંદરની વક્રસપાટી અંતર્ગોળ અરીસાની જેમ વર્તે છે.

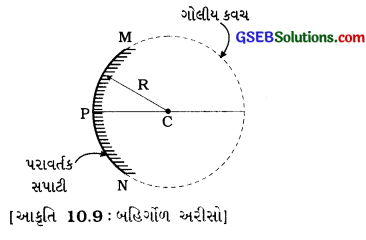
(2) બહિર્ગોળ અરીસો જે ગોલીય અરીસાની પરાવર્તક સપાટી બહારની તરફ વક્રાકાર હોય, તેને બહિર્ગોળ અરીસો કહે છે.
મુખ્ય અક્ષને સમાંતર કિરણપુંજ આ અરીસા વડે પરાવર્તન 3 પામી, એક બિંદુએથી વિકેન્દ્રિત થતા હોય તેવો ભાસ થાય છે. તેથી ? તેને અપસારી અરીસો કહે છે.
દા. ત., ચકચકિત ચમચીની બહારની વક્રસપાટી બહિગળ ‘ અરીસાની જેમ વર્તે છે.

પ્રશ્ન 13.
ગોલીય અરીસાના સંદર્ભમાં નીચેનાં પદો વ્યાખ્યા આપી સમજાવો:
(1) ધ્રુવ
(2) વક્રતાકેન્દ્ર
(3) વક્રતાત્રિયા
(4) મુખ્ય અક્ષ
(5) મુખ્ય કેન્દ્ર
(6) કેન્દ્રલંબાઈ
(7) દર્પણમુખ.
તેમને સમજાવતી સ્વચ્છ નામનિર્દેશવાળી આકૃતિઓ દોરો.
ઉત્તર:

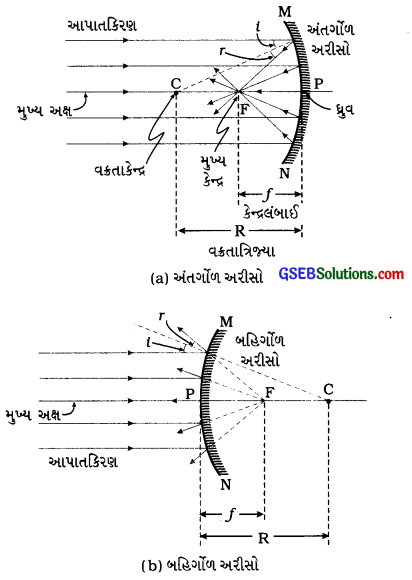
(આકૃતિ 10.10: ગોલીય અરીસા વડે પરાવર્તન)

(1) ધ્રુવઃ ગોલીય અરીસાની પરાવર્તક સપાટીના કેન્દ્ર(મધ્યબિંદુ)ને ગોલીય અરીસાનો ધ્રુવ કહે છે.

• તેને P વડે દર્શાવાય છે.
• ધ્રુવ અરીસાની સપાટી પર હોય છે.

(2) વક્રતાકેન્દ્ર ગોલીય અરીસાની પરાવર્તક સપાટી જે પહેલા ગોળાનો એક ભાગ છે, તેના કેન્દ્રને ગોલીય અરીસાનું વક્રતાકેન્દ્ર કહે છે.

• તેને C વડે દર્શાવાય છે.
• વક્રતાકેન્દ્ર એ અરીસાનો ભાગ નથી. તે અરીસાની પરાવર્તક સપાટીની બહારના ભાગમાં હોય છે.
• અંતર્ગોળ અરીસાનું વક્રતાકે તેની સામે (આગળ) હોય છે, જ્યારે બહિર્ગોળ અરીસાનું વક્રતાકેન્દ્ર તેની પાછળ હોય છે.

(૩) વક્રતા ત્રિજ્યા ગોલીય અરીસાની પરાવર્તક સપાટી જે પોલા ગોળાનો એક ભાગ છે, તેની ત્રિજ્યાને ગોલીય અરીસાની વક્રતાત્રિજ્યા કહે છે.

• તેને R વડે દર્શાવાય છે.
• અંતર PC ગોલીય અરીસાની વક્રતાત્રિજ્યા દર્શાવે છે. PC = R (જુઓ આકૃતિ 10.10)

(4) મુખ્ય અક્ષઃ ગોલીય અરીસાના ધ્રુવ (P) અને વક્રતાકેન્દ્ર (C)માંથી પસાર થતી કાલ્પનિક રેખાને ગોલીય અરીસાનો મુખ્ય અક્ષ કહે છે.

• મુખ્ય અક્ષ એ ગોલીય અરીસાને ધ્રુવ આગળ લંબ હોય છે.

(5) મુખ્ય કેન્દ્રઃ અંતર્ગોળ અરીસા પર આપાત થતાં મુખ્ય અક્ષને સમાંતર પ્રકાશના કિરણો અરીસા દ્વારા પરાવર્તન પામી, મુખ્ય અક્ષ પરના જે બિંદુએ કેન્દ્રિત થાય છે, તે બિંદુને અંતર્ગોળ અરીસાનું મુખ્ય કેન્દ્ર કહે છે.

બહિગોળ અરીસા પર આપાત થતા મુખ્ય અક્ષને સમાંતર પ્રકાશનાં કિરણો અરીસા દ્વારા પરાવર્તન પામી, મુખ્ય અક્ષ પરના જે બિંદુએથી આવતાં હોય તેવો ભાસ થાય છે, તે બિંદુને બહિર્ગોળ અરીસાનું મુખ્ય કેન્દ્ર કહે છે.

• તેને F વડે દર્શાવાય છે.
• અંતર્ગોળ અરીસાનું મુખ્ય કેન્દ્ર અરીસાની સામે (આગળ) હોય છે અને તે વાસ્તવિક બિંદુ છે.
• બહિર્ગોળ અરીસાનું મુખ્ય કેન્દ્ર અરીસાની પાછળ હોય છે અને તે આભાસી બિંદુ છે.

(6) કેન્દ્રલંબાઈઃ ગોલીય અરીસાના ધ્રુવ અને મુખ્ય કેન્દ્ર વચ્ચેના અંતરને અરીસાની કેન્દ્રલંબાઈ કહે છે.

• તેને f વડે દર્શાવાય છે.
• અંતર PF ગોલીય અરીસાની કેન્દ્રલંબાઈ દર્શાવે છે. PF = (જુઓ આકૃતિ 10.10)

(7) દર્પણમુખઃ ગોલીય અરીસાની પરાવર્તક સપાટીની વર્તુળાકાર ધારના વ્યાસને તેનું દર્પણમુખ કહે છે.

• અંતર MN = ગોલીય અરીસાનું દર્પણમુખ. (જુઓ આકૃતિ 10.10)

પ્રશ્ન 14.
ગોલીય અરીસા વડે રચાતું પ્રતિબિંબ મેળવવા ઓછામાં ઓછાં કેટલાં કિરણોની જરૂર છે? શા માટે?
ઉત્તર:
ગોલીય અરીસા વડે રચાતા વસ્તુના પ્રતિબિંબનું સ્થાન કિરણાકૃતિ દોરીને નક્કી કરી શકાય છે.

• આ માટે વસ્તુના કોઈ એક બિંદુ પરથી નીકળતાં કિરણો મોટી સંખ્યામાં લઈ શકાય. પરંતુ સ્પષ્ટ કિરણાકૃતિ દોરવા માટે ફક્ત બે જ કિરણો પૂરતાં છે, કારણ કે બિંદુવત્ વસ્તુના પ્રતિબિંબનું સ્થાન બે પરાવર્તિતકિરણોના છેદબિંદુ દ્વારા પ્રાપ્ત થાય છે.

પ્રશ્ન 15.
ગોલીય અરીસા વડે રચાતું બિંદુવતું વસ્તુનું પ્રતિબિંબ મેળવવા માટે મુખ્ય કયાં ચાર કિરણોનો ઉપયોગ કરવામાં આવે છે? કિરણાકૃતિ દોરીને સમજાવો.
અથવા
(વસ્તુબિંદુમાંથી આવતાં) ભિન્ન પ્રકારનાં કિરણો લઈ ગોલીય અરીસા વડે રચાતાં પ્રતિબિંબનું સ્થાન કેવી રીતે નક્કી કરવામાં આવે છે, તે જરૂરી કિરણાકૃતિઓ દોરી સમજાવો.
ઉત્તર:
(1) કિરણ 1 (મુખ્ય અને સમાંતર કિરણ) મુખ્ય અક્ષની સમાંતર દિશામાં આપાત થતું કિરણ અંતર્ગોળ અરીસા પરથી પરાવર્તન પામી તેના મુખ્ય કેન્દ્ર (F)માંથી પસાર થાય છે અથવા બહિર્ગોળ અરીસાના મુખ્ય કેન્દ્ર (F) પરથી વિકેન્દ્રિત થતું હોય તેવો ભાસ થાય છે. (જુઓ આકૃતિ 10.13)

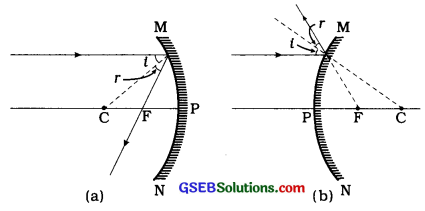
[આકૃતિ 10.13: ગોલીય અરીસાની મુખ્ય અક્ષની સમાંતર દિશામાં આપાત થતું કિરણ (a) અંતર્ગોળ અરીસા માટે (b) બહિર્ગોળ અરીસા માટે.

(2) કિરણ 2 (મુખ્ય કેન્દ્રમાંથી પસાર થતું કિરણ): જો પ્રકાશનું કિરણ અંતર્ગોળ અરીસાના મુખ્ય કેન્દ્ર (F)માંથી પસાર થતું હોય અથવા બહિર્ગોળ અરીસાના મુખ્ય કેન્દ્ર (F)ની દિશા તરફ ગતિ કરતું હોય, તો કિરણ પરાવર્તન પામી મુખ્ય અને સમાંતર દિશામાં પરાવર્તિત થાય છે. (જુઓ આકૃતિ 10.14)

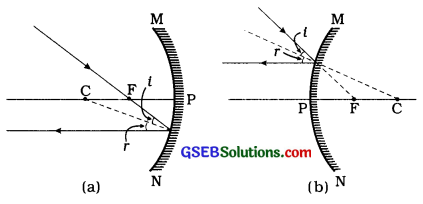
આકૃતિ 10.14: (a) અંતર્ગોળ અરીસાના મુખ્ય કેન્દ્ર (F) માંથી પસાર થતું કિરણ (B) બહિર્ગોળ અરીસાના મુખ્ય કેન્દ્ર (F)ની દિશા તરફ ગતિ કરતું કિરણ]

(૩) કિરણ ૩ (વક્રતાકેન્દ્રમાંથી પસાર થતું કિરણ) અંતર્ગોળ અરીસાના વક્રતાકેન્દ્ર (C)માંથી પસાર થતું અથવા બહિર્ગોળ અરીસાના વક્રતાકેન્દ્ર (C)ની દિશા તરફ ગતિ કરતું પ્રકાશનું કિરણ અરીસા પરથી પરાવર્તન પામી તે જ પથ પર પાછું ફરે છે. (જુઓ આકૃતિ 10.15)
કારણઃ વક્રતાકેન્દ્રમાંથી પસાર થતું આપાતકિરણ અરીસાની પરાવર્તક સપાટીને લંબ હોય છે.

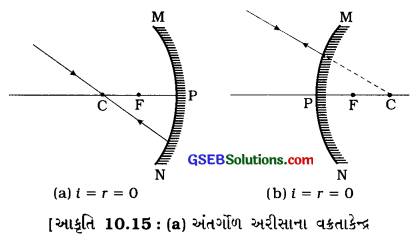
(4) કિરણ 4 (અરીસાના મુખ્ય અક્ષ સાથે નિશ્ચિત કોણ બનાવી ધ્રુવ (P) પર આપાત થતું કિરણ) અંતર્ગોળ અરીસાના કે બહિર્ગોળ અરીસાના મુખ્ય અક્ષ સાથે નિશ્ચિત કોણ બનાવી દિશામાં ધ્રુવ (P) પર આપાત થતું કિરણ મુખ્ય અક્ષ સાથે તેટલો જ નિશ્ચિત કોણ બનાવી પરાવર્તન પામે છે. (જુઓ આકૃતિ 10.16)

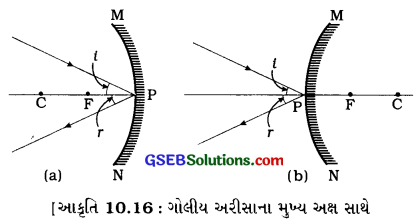
નિશ્ચિત કોણ બનાવી ધ્રુવ (P) પર આપાત થતું કિરણ
(a) અંતર્ગોળ અરીસા માટે
(b) બહિર્ગોળ અરીસા માટે]

અંતર્ગોળ અરીસા વડે રચાતાં પ્રતિબિંબો

પ્રશ્ન 16.
નાના દર્પણમુખવાળા અંતર્ગોળ અરીસા સામે વસ્તુને નીચે દર્શાવેલ સ્થાને મૂકવામાં આવે, તો મળતા પ્રતિબિંબના સ્થાન, પ્રકાર અને પરિમાણનું કિરણાકૃતિ દોરી વર્ણન કરોઃ
(1) અનંત અંતરે
(2) c (વક્રતાકેન્દ્ર)થી દૂર
(3) c (વક્રતાકેન્દ્ર) પર
(4) C (વક્રતાકેન્દ્રો અને F (મુખ્ય કેન્દ્ર)ની વચ્ચે
(5) F (મુખ્ય કેન્દ્રો પર
(6) P (ધ્રુવ) અને F (મુખ્ય કેન્દ્ર)ની વચ્ચે
ઉત્તર:
(1) વસ્તુનું સ્થાન અનંત અંતરે

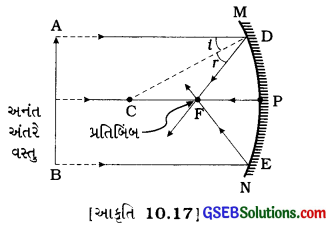
પ્રતિબિંબનું સ્થાન મુખ્ય કેન્દ્ર (F) પર
પ્રતિબિંબનો પ્રકારઃ વાસ્તવિક અને ઊલટું
પ્રતિબિંબનું પરિમાણ વસ્તુ કરતાં ખૂબ નાનું બિંદુવત્

(2) વસ્તુનું સ્થાનઃ C (વક્રતાકેન્દ્ર)થી દૂર પરિમિત અંતરે

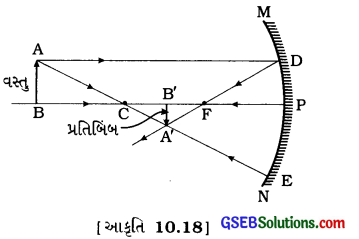
પ્રતિબિંબનું સ્થાન: F અને Cની વચ્ચે
પ્રતિબિંબનો પ્રકારઃ વાસ્તવિક અને ઊલટું
પ્રતિબિંબનું પરિમાણ વસ્તુ કરતાં નાનું

(૩) વસ્તુનું સ્થાન C (વક્રતાકેન્દ્રો પર

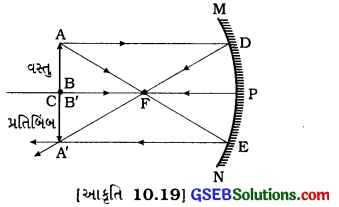
પ્રતિબિંબનું સ્થાન C (વક્રતાકેન્દ્રો) પર
પ્રતિબિંબનો પ્રકારઃ વાસ્તવિક અને ઊલટું
પ્રતિબિંબનું પરિમાણ વસ્તુના પરિમાણ જેટલું

(4) વસ્તુનું સ્થાનઃ C (વક્રતાકેન્દ્ર) અને F (મુખ્ય કેન્દ્ર)ની વચ્ચે

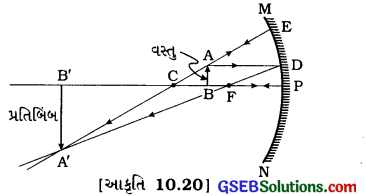
પ્રતિબિંબનું સ્થાનઃ C (વક્રતાકેન્દ્ર)થી દૂર
પ્રતિબિંબનો પ્રકારઃ વાસ્તવિક અને ઊલટું
પ્રતિબિંબનું પરિમાણ વસ્તુ કરતાં મોટું (વિવર્ધિત)

(5) વસ્તુનું સ્થાનઃ F (મુખ્ય કેન્દ્રો પર

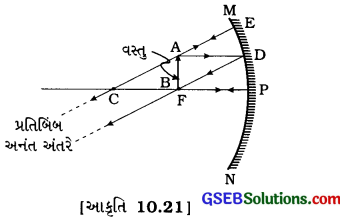
પ્રતિબિંબનું સ્થાન અનંત અંતરે
પ્રતિબિંબનો પ્રકારઃ વાસ્તવિક અને ઊલટું
પ્રતિબિંબનું પરિમાણ વસ્તુ કરતાં ખૂબ જ વિવર્ધિત

(6) વસ્તુનું સ્થાન P (ધ્રુવ) અને F (મુખ્ય કેન્દ્ર)ની વચ્ચે

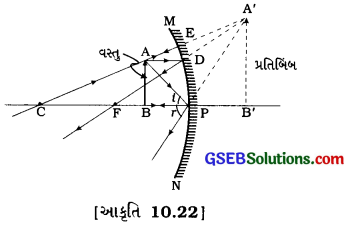
પ્રતિબિંબનું સ્થાનઃ અરીસાની પાછળ
પ્રતિબિંબનો પ્રકારઃ આભાસી અને ચતું
પ્રતિબિંબનું પરિમાણ વસ્તુ કરતાં વિવર્ધિત
[નોંધઃ પ્રતિબિંબ આભાસી હોવાથી તૂટક રેખા વડે દર્શાવેલ છે.]

પ્રશ્ન 17.
ગોલીય અરીસા વડે થતા પરાવર્તન માટેની નવી કાર્તેઝિયન સંજ્ઞા પ્રણાલી સમજાવો.
ઉત્તરઃ
ગોલીય અરીસા વડે થતા પરાવર્તન માટેની નવી કાર્તેઝિયન સંજ્ઞા પ્રણાલી નીચે મુજબ છે :

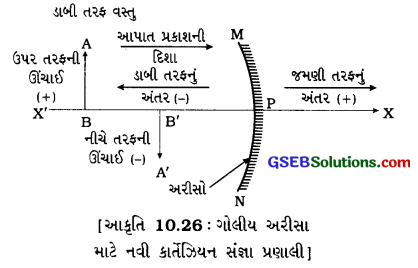
આકૃતિ 10.26માં દર્શાવ્યા પ્રમાણે નવી કાર્તેઝિયન યામપદ્ધતિમાં અરીસાના ધ્રુવ (P)ને ઊગમબિંદુ તરીકે લેવામાં આવે છે. અરીસાના મુખ્ય અક્ષને યામપદ્ધતિના X-અક્ષ (XX) તરીકે લેવામાં આવે છે અને અરીસાના ધ્રુવ (P) આગળ મુખ્ય અક્ષને દોરેલા લંબને Y-અક્ષ તરીકે લેવામાં આવે છે.

1. વસ્તુ હંમેશાં અરીસાની ડાબી બાજુ રાખવામાં આવે છે. એટલે કે વસ્તુ પરથી આવતો પ્રકાશ અરીસા પર ડાબી બાજુથી આપાત થાય છે.
2. બધાં જ અંતરો અરીસાના ધ્રુવ (P)થી મુખ્ય અને સમાંતર માપવામાં આવે છે.
3. ઊગમબિંદુ(ધ્રુવ)થી જમણી બાજુ (+ X-અક્ષની દિશામાં) માપેલ બધાં જ અંતરો ધન અને ઊગમબિંદુથી ડાબી બાજુ (-X-અક્ષની દિશામાં) માપેલ બધાં જ અંતરો ત્રણ લેવામાં આવે છે.
4. મુખ્ય અક્ષને લંબરૂપે ઉપરની તરફ (+Y-અક્ષની દિશામાં) માપેલ ઊંચાઈ ધન લેવામાં આવે છે.
5. મુખ્ય અક્ષને લંબરૂપે નીચેની તરફ (- Y-અક્ષની દિશામાં) માપેલ ઊંચાઈ કણ લેવામાં આવે છે.

પ્રશ્ન 18.
અરીસાનું સૂત્ર એટલે શું? તેને ગાણિતિક સ્વરૂપમાં લખો.
ઉત્તર:
વસ્તુ-અંતર (u), પ્રતિબિંબ-અંતર (D) અને અરીસાની કેન્દ્રલંબાઈ f) વચ્ચેનો સંબંધ દર્શાવતા સૂત્રને અરીસાનું સૂત્ર કહે છે.
અરીસાના સૂત્રનું ગાણિતિક સ્વરૂપ નીચે મુજબ છે :
\(\frac{1}{v}\) + \(\frac{1}{u}\) = \(\frac{1}{f}\) … …. (10.4)
જ્યાં, u = વસ્તુ – અંતર
v = પ્રતિબિંબ – અંતર
f = અરીસાની કેન્દ્રલંબાઈ
નોંધઃ

1. અરીસાનું સૂત્ર દરેક અરીસા અને વસ્તુનાં બધાં સ્થાનો માટે સારું છે.
2. અરીસાના કોયડા(દાખલા)ના ઉકેલ માટે અરીસાના સૂત્રમાં u, y, f અને Rની કિંમતો નવી કાર્તેઝિયન સંજ્ઞા પ્રણાલી મુજબ મૂકવી.

પ્રશ્ન 19.
અરીસા વડે મળતી મોટવણી વિશે ટૂંક નોંધ લખો.
ઉત્તર:
ગોલીય અરીસા વડે મળતી મોટવણી એ વસ્તુનું પ્રતિબિંબ વસ્તુના કદની સાપેક્ષે કેટલા ગણું વિવર્ધિત છે તેનો સંબંધ આપે છે.

• પ્રતિબિંબની ઊંચાઈ અને વસ્તુની ઊંચાઈના ગુણોત્તરને મોટવણી કહે છે.
• મોટવણી(Magnification)ને m વડે દર્શાવાય છે.
• જો વસ્તુની ઊંચાઈ h હોય અને પ્રતિબિંબની ઊંચાઈ h’ હોય, તો ગોલીય અરીસાની મોટવણી નીચેના સૂત્રથી મળે છે :
  
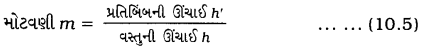
• વળી, મોટવણી m એ વસ્તુ-અંતર u અને પ્રતિબિંબ-અંતર છે સાથે સંબંધ ધરાવે છે, જે નીચે મુજબ છે :
  મોટવણી m = –\(\frac{v}{u}\) …… (10.6)
• સામાન્ય રીતે વસ્તુ મુખ્ય અક્ષની ઉપર રાખવામાં આવતી હોવાથી, રે વસ્તુની ઊંચાઈ h ઉપરની તરફ માપવામાં આવે છે. તેથી તેનું મૂલ્ય ધન લેવામાં આવે છે.
• આભાસી પ્રતિબિંબની ઊંચાઈ h’ ધન જ્યારે વાસ્તવિક પ્રતિબિંબની ઊંચાઈ માટે h’ ઋણ લેવામાં આવે છે.
• મોટવણીના મૂલ્યમાં ત્રણ ચિહ્ન, પ્રતિબિંબ વાસ્તવિક છે તેમ સૂચવે છે.
• મોટવણીના મૂલ્યમાં ધન ચિહ્ન, પ્રતિબિંબ આભાસી છે તેમ સૂચવે છે.

પ્રશ્ન 20.
અંતર્ગોળ અરીસાના કિસ્સામાં મોટવણીનું સૂત્ર m = –\(\frac{v}{u}\) મેળવો.
ઉત્તર:
આપણે જાણીએ છીએ કે, મોટવણી

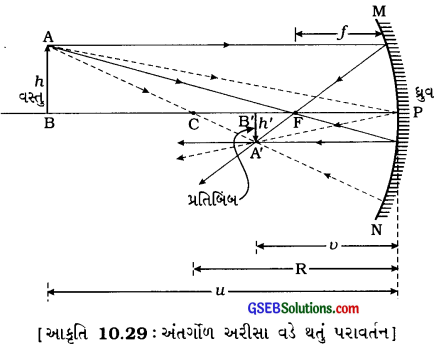
• આકૃતિ 10.29માં વસ્તુ ABનું અંતર્ગોળ અરીસા વડે મળતું પ્રતિબિંબ A’B’ દર્શાવેલ છે.
• આકૃતિમાં, કાટકોણ ત્રિકોણો ∆A’B’P અને ∆ ABP સમરૂપ ત્રિકોણો છે.
  ∴ \(\frac{\mathrm{A}^{\prime} \mathrm{B}^{\prime}}{\mathrm{AB}}\) = \(\frac{\mathrm{PB}^{\prime}}{\mathrm{PB}}\) .. … (10.8)
  જ્યાં, A’B’ = પ્રતિબિંબની ઊંચાઈ = + h
  AB = વસ્તુની ઊંચાઈ = + h
  PB’ = પ્રતિબિંબ-અંતર = -v
  PB = વસ્તુ-અંતર = -u
  ∴ \(\frac{-h^{\prime}}{h}\) = \(\frac{-v}{-u}\) = \(\frac{v}{u}\)
  ∴ \(\frac{h^{\prime}}{h}\) = –\(\frac{v}{u}\) … (10.9)
• સમીકરણ (10.7) અને (10.9) પરથી,
  m = –\(\frac{v}{u}\) … … (10.10)

પ્રશ્ન 21.
સમતલ અરીસા વડે મળતા વસ્તુના પ્રતિબિંબનું સ્થાન, પ્રકાર અને પરિમાણ મોટવણીના સૂત્ર પરથી મેળવો.
ઉત્તર:
સમતલ અરીસા વડે મળતા વસ્તુના પ્રતિબિંબની કિરણાકૃતિ આકૃતિ 10.30માં દર્શાવી છે.

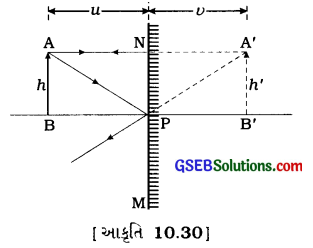
• આકૃતિ પરથી સ્પષ્ટ છે કે વસ્તુની ઊંચાઈ (h) અને પ્રતિબિંબની ઊંચાઈ (h’) સમાન છે. એટલે કે h’ = h

∴ મોટવણી m = \(\frac{h^{\prime}}{h}\) = \(\frac{h}{h}\) = 1
અથવા
વસ્તુ-અંતર PB = -u
પ્રતિબિંબ-અંતર PB’ = +D
∴ મોટવણી m = – \(\frac{v}{u}\) = –\(\frac{v}{(-u)}\) = \(\frac{v}{u}\)

અત્રે, મોટવણી ધન મળે છે, જે દર્શાવે છે કે પ્રતિબિંબ ચતું હશે, તેથી આભાસી હશે તથા m =1 પરથી પ્રતિબિંબનું પરિમાણ વસ્તુના પરિમાણ જેટલું છે.

• ટૂંકમાં, સમતલ અરીસા વડે રચાતું પ્રતિબિંબ આભાસી, ચતું અને વસ્તુના કદ જેટલું જ હોય છે.

∴ મોટવણીના વ્યાપક સૂત્ર m = \(\frac{v}{u}\) પરથી, I = – \(\frac{v}{u}\) = થાય.
∴ v = -u
જે દર્શાવે છે કે, સમતલ અરીસાથી વસ્તુ જેટલા અંતરે આગળ હોય છે, તેટલા જ અંતરે પ્રતિબિંબ અરીસાના પાછળના ભાગમાં રચાય છે.

પ્રશ્ન 22.
અરીસાના સૂત્ર \(\frac{1}{u}\) + \(\frac{1}{v}\) = \(\frac{1}{f}\) પરથી સમતલ અરીસામાં પ્રતિબિંબનું સ્થાન કેવી રીતે નક્કી કરશો?
ઉત્તરઃ
સમતલ અરીસાની વક્રતાત્રિજ્યા (R) = અનંત (∞) અને કેન્દ્રલંબાઈ f = અનંત (∞) છે.
∴ અરીસાના સૂત્ર પરથી,
\(\frac{1}{(-u)}\) + \(\frac{1}{v}\) = \(\frac{1}{\infty}\) (સંજ્ઞા પ્રણાલી વાપરતાં)
∴ –\(\frac{1}{u}\) + \(\frac{1}{v}\) = 0
∴ u = 0
તેથી કહી શકાય કે, સમતલ અરીસાથી વસ્તુ જેટલા અંતરે આગળ હોય છે, તેટલા જ અંતરે પ્રતિબિંબ અરીસાના પાછળના ભાગમાં રચાય છે.

પ્રશ્ન 23.
પાણી ભરેલા કાચના પ્યાલામાં અંશતઃ ડુબાડેલ પેન્સિલ હવા અને પાણીના આંતરપૃષ્ઠ આગળ વાંકી વળેલ શા માટે દેખાય છે?
ઉત્તરઃ
પેન્સિલના પાણીમાં ડૂબેલા ભાગ પરથી આવતાં પ્રકાશનાં કિરણો પાણીમાંથી હવામાં પ્રવેશે છે, ત્યારે પાણીની સપાટી આગળથી વક્રીભવન પામે છે. વક્રીભવન બાદ આપણી આંખ તરફ આવતાં પ્રકાશનાં કિરણો, પેન્સિલના પાણીની બહાર રહેલા ભાગની સરખામણીમાં અલગ દિશામાંથી આવતાં જણાય છે. તેના કારણે પેન્સિલ હવા અને પાણીના આંતરપૃષ્ઠ આગળ વાંકી વળેલ દેખાય છે.

અગત્યની નોંધઃ અક્ષરોની ઉપર કાચનો સ્લેબ રાખીને જોતાં અક્ષરો ઉપર તરફ ખસેલા દેખાય છે. પાણી ભરેલા કાચના પ્યાલામાં સિક્કો ઉપર તરફ ખસેલો દેખાય છે. પાણી ભરેલા કાચના પ્યાલામાં લીંબુ નાખી બાજુએથી જોતાં તે મૂળ કદ કરતાં મોટું દેખાય છે.

ઉપરાંત, અલગ અલગ માધ્યમોની જોડ માટે આ અસરનું પ્રમાણ અલગ અલગ હોય છે. દા. ત., હવા અને પાણીની જોડ કરતાં હવા અને કેરોસીન કે ટર્પેન્ટાઇનની જોડ માટે પેન્સિલનું વાંકા વળવાનું પ્રમાણ અલગ હોય છે. આ જ પ્રમાણે તળિયે સિક્કો ધરાવતાં કાચના પ્યાલામાં, પાણીના બદલે બીજું કોઈ પ્રવાહી ભરવામાં આવે તો સિક્કાનું ઉપર તરફ ખસવાનું પ્રમાણ બદલાઈ જાય છે.

આ અવલોકનો દર્શાવે છે કે, પ્રકાશ ત્રાંસી દિશામાં એક પારદર્શક માધ્યમમાંથી બીજા પારદર્શક માધ્યમમાં ગતિ કરે છે ત્યારે બીજા માધ્યમમાં પ્રકાશના પ્રસરણની દિશા બદલાઈ જાય છે. આ બદલાવ બે માધ્યમોને જોડતી સપાટી આગળ થાય છે.

પ્રશ્ન 24.
પ્રકાશનું વક્રીભવન એટલે શું? અથવા પ્રકાશના વક્રીભવનની વ્યાખ્યા આપો.
ઉત્તર:
જ્યારે પ્રકાશનું ત્રાંસું કિરણ એક પારદર્શક માધ્યમમાંથી બીજા પારદર્શક માધ્યમમાં પ્રવેશે છે ત્યારે બે માધ્યમોને છૂટી પાડતી સપાટી આગળ કિરણના પ્રસરણની દિશા બદલાય છે. આ ઘટનાને પ્રકાશનું વક્રીભવન કહે છે.

અથવા

જ્યારે પ્રકાશનું ત્રાંસું કિરણ એક પારદર્શક માધ્યમમાંથી બીજા પારદર્શક માધ્યમમાં ગતિ કરે છે ત્યારે બે માધ્યમોને છૂટી પાડતી સપાટી આગળ વાંકું વળે છે. પ્રકાશના કિરણની વાંકા વળવાની ક્રિયાને પ્રકાશનું વક્રીભવન કહે છે.

અથવા

એક પારદર્શક માધ્યમમાંથી બીજા પારદર્શક માધ્યમમાં પ્રવેશતા પ્રકાશના ત્રાંસા કિરણની ઝડપ બદલાઈ જાય છે. પરિણામે બે માધ્યમોને છૂટી પાડતી સપાટી આગળ પ્રકાશના પ્રસરણની દિશા બદલાય છે. આ ઘટનાને પ્રકાશનું વક્રીભવન કહે છે.

પ્રશ્ન 25.
માધ્યમનો વક્રીભવનાંક (The refractive index) એટલે શું?
ઉત્તર:
પ્રકાશનું ત્રાંસું કિરણ એક પારદર્શક માધ્યમમાંથી બીજા પારદર્શક માધ્યમમાં પ્રવેશ કરે છે ત્યારે બીજા માધ્યમમાં તે પોતાની દિશા બદલે છે.

• આપેલ કોઈ પણ બે માધ્યમોની જોડ માટે થતા દિશાના આ ફેરફાર(પરિવર્તન)નું પ્રમાણ વક્રીભવનાંક સ્વરૂપે રજૂ કરવામાં આવે છે. સમીકરણ \(\frac{\sin i}{\sin r}\) = અચળમાં અચળ મૂલ્યને વક્રીભવનાંક કહે છે.

પ્રશ્ન 26.
વક્રીભવનાંક સમજાવો. અથવા સાપેક્ષ વક્રીભવનાંક સમજાવો.
ઉત્તર:
શૂન્યાવકાશમાં પ્રકાશની ઝડપ એ કુદરતમાં મૂળભૂત અચળાંક છે. તેને તે વડે દર્શાવાય છે.

• સામાન્ય હેતુઓ માટે, પ્રકાશની શૂન્યાવકાશમાં ઝડપ

c = 3 × 10⁸ m s^-1 લેવામાં આવે છે.

• પ્રકાશની હવામાં ઝડપ એ શૂન્યાવકાશમાં પ્રકાશની ઝડપ કરતાં સહેજ જ ઓછી છે. આથી પ્રકાશની હવામાં ઝડપ પણ 3 × 10⁸ m s^-1 લેવામાં આવે છે.
• વક્રીભવનાંક એ જુદાં જુદાં માધ્યમોમાં પ્રકાશના પ્રસરણ દરમિયાન મળતી સાપેક્ષ ઝડપને સાંકળતી મહત્ત્વપૂર્ણ ભૌતિક રાશિ છે. જુદાં જુદાં માધ્યમોમાં પ્રકાશ જુદી જુદી ઝડપે પ્રસરણ પામે છે.
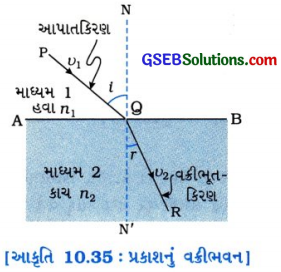
• આકૃતિ 10.35 મુજબ, પ્રકાશનું કિરણ માધ્યમ 1માંથી માધ્યમ 2માં ગતિ કરે છે એમ ધારો.
• માધ્યમ 1માં તેની ઝડપ , અને માધ્યમ 2માં ઝડપ 02 લો.
• માધ્યમ માં પ્રકાશની ઝડપ છે, અને માધ્યમ 2માં પ્રકાશની ઝડપ v₂ ના ગુણોત્તરથી માધ્યમ 2નો માધ્યમ 1ની સાપેક્ષે વક્રીભવનાંક મળે છે.
• તેને n₂₁ વડે દર્શાવાય છે.
• 

પ્રશ્ન 27.
નિરપેક્ષ વક્રીભવનાંક સમજાવો.
ઉત્તર:
આપેલ માધ્યમનો શૂન્યાવકાશની સાપેક્ષે વક્રીભવનાંક તે માધ્યમનો નિરપેક્ષ વક્રીભવનાંક કહેવાય છે.
તે શૂન્યાવકાશમાં પ્રકાશની ઝડપ (C) અને આપેલ માધ્યમમાં પ્રકાશની ઝડપ (D)નો ગુણોત્તર છે. તેને n_m વડે દર્શાવાય છે.

• નિરપેક્ષ વક્રીભવનાંક’ને ‘વક્રીભવનાંક પણ કહે છે.
• દા. ત., જો કાચમાં પ્રકાશની ઝડપ 2 × 10⁸ m s^-1 હોય, તો કાચનો નિરપેક્ષ વક્રીભવનાંક,
  n_g = \(\frac{3 \times 10^{8}}{2 \times 10^{8}}\)
  = \(\frac{3}{2}\) = 1.5
• કોઈ પણ માધ્યમનો નિરપેક્ષ વક્રીભવનાંક હંમેશાં 1 કરતાં વધુ હોય છે.
• નિરપેક્ષ વક્રીભવનાંક એકમ રહિત સાદો આંક છે.
  [નોંધઃ વ્યવહારમાં હવામાં પ્રકાશની ઝડપને શૂન્યાવકાશમાં પ્રકાશની ઝડપ જેટલી ગણવામાં આવે છે. તેથી હવાનો નિરપેક્ષ વક્રીભવનાંક n_a = 1 થાય.].
  ટેબલ 2: કેટલાંક દ્રવ્ય માધ્યમોના નિરપેક્ષ વક્રીભવનાંક
  
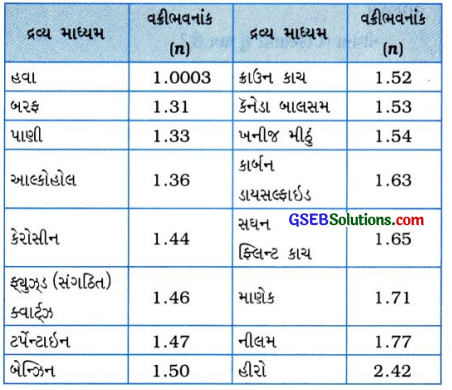
  ટેબલ 2 પરથી નોંધો કે, વધુ દળ ઘનતા (Mass density) ધરાવતું માધ્યમ પ્રકાશીય ઘટ્ટ હોય, તે જરૂરી નથી.

ઉદાહરણ તરીકે, કેરોસીનની દળ ઘનતા પાણીની દળ ઘનતા કરતાં ઓછી છે. છતાં કેરોસીનની પ્રકાશીય ઘનતા પાણીની પ્રકાશીય. ઘનતા કરતાં વધુ છે.

પ્રશ્ન 28.
પાણીનો વક્રીભવનાંક 1.33 છે. આનો અર્થ શો થાય?
ઉત્તર:
પાણીનો વક્રીભવનાંક n_w = 1.33 છે. તેનો અર્થ એ 3 થાય કે પ્રકાશની શૂન્યાવકાશમાં ઝડપ અને પ્રકાશની પાણીમાં ઝડપનો ગુણોત્તર 1.33 છે.

પ્રશ્ન 29.
માધ્યમની પ્રકાશીય ઘનતા એટલે શું? તેના વિશે ૨ ટૂંકમાં માહિતી આપો.
ઉત્તર:
પ્રકાશને વક્રીભૂત કરવાની માધ્યમની ક્ષમતાને માધ્યમની પ્રકાશીય ઘનતા કહે છે. પ્રકાશીય ઘનતા ચોક્કસ સૂચિતાર્થ ધરાવે છે. તે અને દળ ઘનતા સમાન નથી.

પ્રશ્ન 30.
પ્રકાશીય ઘટ્ટ માધ્યમ અને પ્રકાશીય પાતળું માધ્યમ એટલે શું?
ઉત્તર:
બે માધ્યમોની સરખામણી કરતી વખતે વધારે વક્રીભવનાંક ધરાવતું માધ્યમ બીજા માધ્યમની સાપેક્ષે પ્રકાશીય ઘટ્ટ માધ્યમ કહેવાય છે. જ્યારે ઓછો વક્રીભવનાંક ધરાવતું બીજું માધ્યમ પ્રકાશીય પાતળું માધ્યમ કહેવાય છે.

• પ્રકાશીય પાતળા માધ્યમમાં પ્રકાશની ઝડપ પ્રકાશીય ઘટ્ટ માધ્યમની સાપેક્ષે વધારે હોય છે.
• પ્રકાશનું ત્રાંસું કિરણ જ્યારે પ્રકાશીય પાતળા માધ્યમમાંથી પ્રકાશીય ઘટ્ટ માધ્યમમાં પ્રવેશે છે, ત્યારે ઘીમું પડે છે અને આપાતબિંદુએ દોરેલા લંબ તરફ વાંકું વળે છે. જ્યારે પ્રકાશીય ઘટ્ટ માધ્યમમાંથી પ્રકાશીય પાતળા માધ્યમમાં પ્રવેશે છે, ત્યારે ઝડપી બને છે અને આપાતબિંદુએ દોરેલા લંબથી દૂર તરફ જાય છે.

પ્રશ્ન 31.
સ્વચ્છ અને નામનિર્દેશવાળી આકૃતિઓ વડે સમજાવો.
નીચેના બે કિસ્સામાં શું થાય છે?
(1) પ્રકાશનું કિરણ પ્રકાશીય પાતળા માધ્યમમાંથી ઘટ્ટ માધ્યમમાં પ્રવેશે ત્યારે
(2) પ્રકાશનું કિરણ પ્રકાશીય ઘટ્ટ માધ્યમમાંથી પાતળા માધ્યમમાં પ્રવેશે ત્યારે
ઉત્તરઃ
સ્નેલના નિયમ અનુસાર,

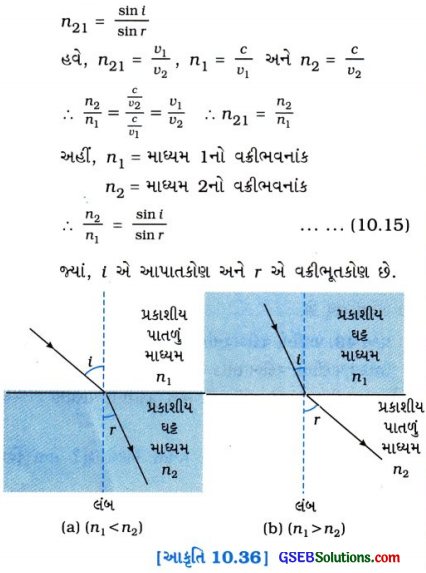
(1)
પ્રકાશનું કિરણ પ્રકાશીય પાતળા માધ્યમમાંથી ઘટ્ટ માધ્યમમાં પ્રવેશે ત્યારે –
અહીં, n₁ < n₂
∴ sin r < sin i ∴ r < i
આ પરથી, વક્રીભૂતકોણ (r) એ આપાતકોણ (i) કરતાં ઓછો છે.

• આ પરથી સ્પષ્ટ થાય છે કે, આ કિસ્સામાં આપાતબિંદુએ પ્રકાશનું કિરણ લંબ તરફ વાંકું વળે છે. (જુઓ આકૃતિ 10.36 (a)].

(2)
પ્રકાશનું કિરણ પ્રકાશીય ઘટ્ટ માધ્યમમાંથી પાતળા માધ્યમમાં પ્રવેશે ત્યારે –
અહીં, n₁ > n₂
∴ sin r > sin i ∴ r > 1
આ પરથી, વક્રીભૂતકોણ (r) એ આપાતકોણ (1) કરતાં વધારે છે.

• આ પરથી સ્પષ્ટ થાય છે કે, આ કિસ્સામાં આપાતબિંદુએ પ્રકાશનું કિરણ લંબથી દૂર તરફ વાંકું વળે છે.
  [જુઓ આકૃતિ 10.36 (b)].

પ્રશ્ન 32.
લેન્સ એટલે શું? અથવા લેન્સની વ્યાખ્યા આપો.
ઉત્તર:
એક અથવા બંને વક્ર સપાટીઓ દ્વારા ઘેરાતા પારદર્શક માધ્યમને લેન્સ કહે છે. લિન્સની ઓછામાં ઓછી એક સપાટી વક્ર હોય છે.
તેની બીજી સપાટી સમતલ હોઈ શકે છે. લેન્સની બંને સપાટી વક્રીભવનકારક સપાટીઓ કહેવાય છે.].

પ્રશ્ન 33.
ડબલ બહિર્ગોળ (ઉભય બાહ્યગોળ – ઉભયોત્તલ) લેન્સ ટૂંકમાં સમજાવો.
ઉત્તર :

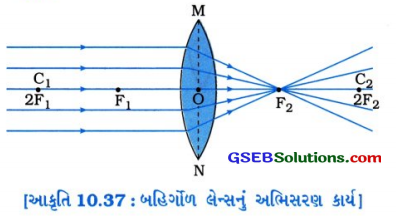
• જે લેન્સની બંને વક્ર સપાટીઓ બહારની તરફ ઉપસેલી હોય છે, તેને ડબલ બહિર્ગોળ લેન્સ અથવા બહિર્ગોળ લેન્સ કહે છે.
• તે તેની કિનારી(ધાર)ની સાપેક્ષે મધ્યમાં જાડો હોય છે.
• બહિર્ગોળ લેન્સ પ્રકાશનાં કિરણોને આકૃતિ 10.37માં દર્શાવ્યા મુજબ અભિસૃત કરે છે. તેથી બહિર્ગોળ લેન્સને ‘અભિસારી લેન્સ’ કહે છે.

પ્રશ્ન 34.
ડબલ અંતર્ગોળ (ઉભયાંતર્ગોળ) લેન્સ ટૂંકમાં સમજાવો.
ઉત્તર:

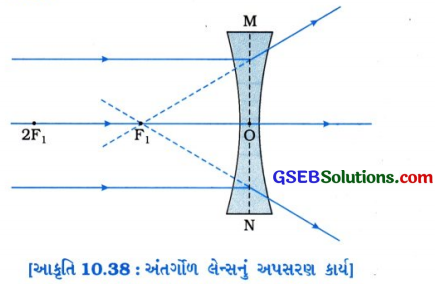
• જે લેન્સની બંને વક્ર સપાટીઓ અંદરની તરફ વળેલી હોય છે, તેને ડબલ અંતર્ગોળ લેન્સ અથવા અંતર્ગોળ લેન્સ કહે છે.
• તે તેની કિનારી(ધાર)ની સાપેક્ષે મધ્યમાં પાતળો હોય છે.
• અંતર્ગોળ લેન્સ પ્રકાશનાં કિરણોને આકૃતિ 10.38માં દર્શાવ્યા પ્રમાણે અપસૂત કરે છે. તેથી અંતર્ગોળ લેન્સને “અપસારી લેન્સ’ કહે છે.

પ્રશ્ન 35.
બહિર્ગોળ લેન્સના સંદર્ભમાં નીચેનાં પદો સમજાવો :
(1) વક્રતાકેન્દ્ર
(2) મુખ્ય અક્ષ
(3) પ્રકાશીય કેન્દ્ર (Optical centre)
(4) લેન્સનું મુખ (Aperture)
(5) વક્રતાત્રિજ્યા
(6) મુખ્ય કેન્દ્ર
(7) કેન્દ્રલંબાઈ
ઉત્તર:

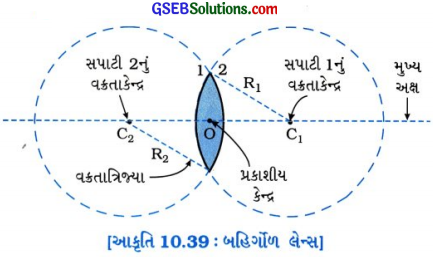
નોંધઃ આકૃતિ 10.39 માત્ર સમજણ માટે છે, પરીક્ષામાં દોરવાની નથી.

(1) વક્રતાકેન્દ્રઃ લેન્સની જે વક્રસપાટી જે પારદર્શક (કાચના) ગોળાનો એક ભાગ હોય, તે ગોળાના કેન્દ્રને લેન્સની તે વક્ર સપાટીનું વક્રતાકેન્દ્ર કહે છે. જે બે ગોળાઓ દ્વારા લેન્સની બે વક્રસપાટીઓ બનેલી હોય તે ગોળાઓના કેન્દ્રને આનુષાંગિક વક્ર સપાટીઓનું વક્રતાકેન્દ્ર કહે છે.
લેન્સને બે વક્રસપાટી છે. તેથી લેન્સનાં બે વક્રતાકેન્દ્રો C₁ અને C₂ છે. લેન્સની પ્રથમ સપાટી(સપાટી 1)નું વક્રતાકેન્દ્ર C₁ છે અને બીજી સપાટી(સપાટી 2)નું વક્રતાકેન્દ્ર C₂ છે. (જુઓ આકૃતિ 10.39)

(2) મુખ્ય અક્ષ લેન્સની બંને સપાટીઓનાં વક્રતાકેન્દ્રો , C₁ અને C₂માંથી પસાર થતી કાલ્પનિક રેખાને લેન્સનો મુખ્ય અક્ષ કહે છે.

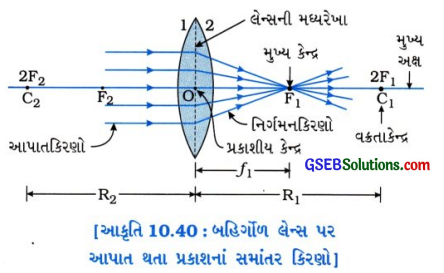
નોંધઃ આકૃતિ 10.40 માત્ર સમજણ માટે છે, પરીક્ષામાં દોરવાની નથી.

(3) પ્રકાશીય કેન્દ્ર (ઑપ્ટિકલ સેન્ટર): લેન્સના મુખ્ય અક્ષ પર આવેલ લેન્સના મધ્ય કેન્દ્રને લેન્સનું પ્રકાશીય કેન્દ્ર કહે છે. સામાન્ય રીતે તેને ‘O’ વડે દર્શાવાય છે. પ્રકાશીય કેન્દ્રમાંથી પસાર થતું કિરણ વક્રીભવન પામતું નથી.

(4) લેન્સનું મુખ (Aperture) : વક્રાકાર (ગોલીય) લેન્સની વર્તુળાકાર કિનારીના અસરકારક વ્યાસને લેન્સનું મુખ (અપર્ચર) કહે છે.

(5) વક્રતા ત્રિજ્યા બહિર્ગોળ લેન્સની જે વક્રસપાટી જે પારદર્શક (કાચના) ગોળાનો એક ભાગ હોય, તે ગોળાની ત્રિજ્યાને લેન્સની તે વક્રસપાટીની વક્રતાત્રિજ્યા (R) કહે છે.
લેન્સને બે વક્રતા ત્રિજ્યા R અને R) હોય છે.

(6) મુખ્ય કેન્દ્ર બહિર્ગોળ લેન્સ પર તેના મુખ્ય અક્ષને સમાંતર આપાત થતાં પ્રકાશનાં કિરણો લેન્સ દ્વારા વક્રીભવન પામીને લેન્સના મુખ્ય અક્ષ પરના જે બિંદુએ કેન્દ્રિત થતા હોય તે બિંદુને બહિર્ગોળ લેન્સનું મુખ્ય કેન્દ્ર F કહે છે.
લેન્સની બંને બાજુએ એક-એક એમ કુલ બે મુખ્ય કેન્દ્રો F₁ અને F₂ હોય છે.
(નોંધઃ બહિર્ગોળ લેન્સ પર તેના મુખ્ય અક્ષને સમાંતર આપાત થતાં પ્રકાશનાં કિરણો લેન્સ દ્વારા વક્રીભવન પામીને લેન્સના મુખ્ય અક્ષ પરના જે બિંદુએ કેન્દ્રિત થતા હોય અથવા અંતર્ગોળ લેન્સના કિસ્સામાં જે બિંદુએથી વિકેન્દ્રિત થતા હોય તેવો ભાસ થતો હોય, તે – બિંદુને લેન્સનું મુખ્ય કેન્દ્ર કહે છે.)

(7) કેન્દ્રલંબાઈ લેન્સના પ્રકાશીય કેન્દ્ર (O) અને મુખ્ય કેન્દ્ર વચ્ચેના અંતરને લેન્સની કેન્દ્રલંબાઈ કહે છે.

• તેનેf વડે દર્શાવાય છે.
• લેન્સની બે કેન્દ્રલંબાઈ f₁ અને f₂ હોય છે.

[O અને F₁ વચ્ચેના અંતરને કેન્દ્રલંબાઈ તથા O અને F₂ વચ્ચેના અંતરને કેન્દ્રલંબાઈ f₂ કહે છે.)

પ્રશ્ન 36.
ગોલીય લેન્સ વડે રચાતાં પ્રતિબિંબ મેળવવા માટે મુખ્ય ક્યા ત્રણ કિરણોનો ઉપયોગ કરવામાં આવે છે? આકૃતિ દોરીને સમજાવો.
ઉત્તર:
ગોલીય લેન્સ વડે રચાતું પ્રતિબિંબ મેળવવા માટે નીચેનાં ત્રણ કિરણોમાંથી કોઈ પણ બે કિરણોનો ઉપયોગ કરવામાં આવે છે :

(1) કિરણ 1 (મુખ્ય અક્ષને સમાંતર કિરણ): વસ્તુ પરથી આવતું બહિર્ગોળ લેન્સના મુખ્ય અક્ષને સમાંતર આપાત થતું કિરણ બહિર્ગોળ લેન્સ દ્વારા વક્રીભવન પામી મુખ્ય કેન્દ્ર F₂ માંથી પસાર થાય છે.

• વસ્તુ પરથી આવતું મુખ્ય અક્ષને સમાંતર પ્રકાશનું કિરણ અંતર્ગોળ લેન્સ વડે વક્રીભવન પામી, મુખ્ય કેન્દ્ર F₁ માંથી અપસરણ પામતું હોય (વિકેન્દ્રિત થતું હોય) તેવો ભાસ થાય છે.
  

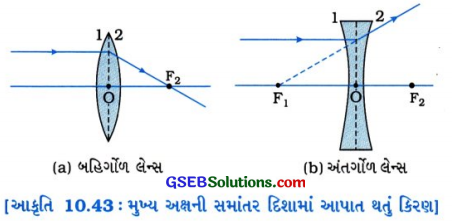
(2) કિરણ 2 (મુખ્ય કેન્દ્રમાંથી પસાર થતું કિરણ) : બહિગળ લેન્સના મુખ્ય કેન્દ્ર F₁ માંથી પસાર થતું કિરણ, બહિર્ગોળ લેન્સ વડે વક્રીભવન પામી મુખ્ય અક્ષને સમાંતર દિશામાં નિર્ગમન પામે છે.

• અંતર્ગોળ લેન્સના મુખ્ય કેન્દ્ર F₂ ની દિશામાં આવતું કિરણ (આપાતકિરણ) વક્રીભવન પામ્યા બાદ મુખ્ય અક્ષને સમાંતર દિશામાં નિર્ગમન પામે છે. (જુઓ આકૃતિ 10.44 (a) અને (b))
  

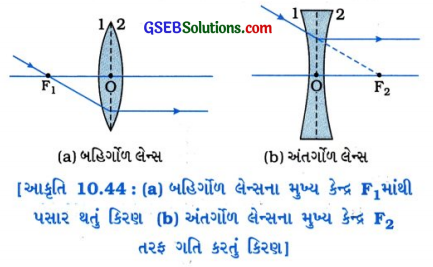
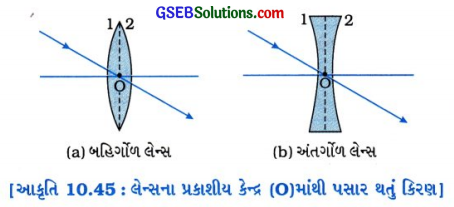
(૩) કિરણ 3 (પ્રકાશીય કેન્દ્રમાંથી પસાર થતું કિરણ) : બહિર્ગોળ અથવા અંતગોંળ લેન્સના પ્રકાશીય કેન્દ્રમાંથી પસાર થતું કિરણ વિચલન પામ્યા સિવાય લેન્સમાંથી નિર્ગમન પામે છે. (જુઓ આકૃતિ 10.45 (2) અને (b)).

પ્રશ્ન 37.
બહિર્ગોળ લેન્સ સામે વિસ્તૃત વસ્તુ ABને નીચે દર્શાવેલ સ્થાને મૂકવામાં આવે, તો મળતા પ્રતિબિંબની કિરણાકૃતિ દોરી, તેના સ્થાન, પ્રકાર અને સાપેક્ષ પરિમાણનું વર્ણન કરો:
(1) અનંત અંતરે
(2) 2F₁ થી થોડે દૂર
(3) 2F₁ પર
(4) F₁ અને 2F₁ ની વચ્ચે
(5) F₁ પર
(6) F₁ અને O વચ્ચે
ઉત્તર:
(1) વસ્તુનું સ્થાન અનંત અંતરે

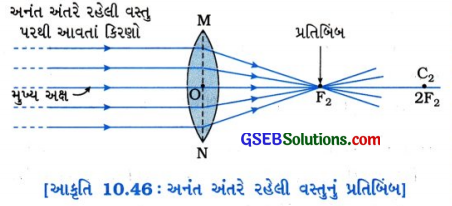
પ્રતિબિંબ પ્રતિબિંબનું સ્થાનઃ વસ્તુની વિરુદ્ધ બાજુએ મુખ્ય કેન્દ્ર (F₂) પર
પ્રતિબિંબનો પ્રકારઃ વાસ્તવિક અને ઊલટું
પ્રતિબિંબનું પરિમાણ અત્યંત નાનું (બિંદુવ)

(2) વસ્તુનું સ્થાન: 2F₁ થી થોડે દૂર

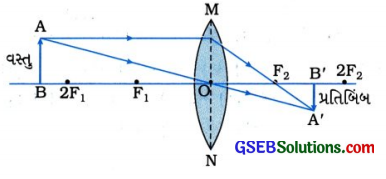
[આકૃતિ 10.47: 2 થી થોડે દૂર મૂકેલી વસ્તુનું પ્રતિબિંબ]
પ્રતિબિંબનું સ્થાનઃ વસ્તુની વિરુદ્ધ બાજુએ F₂ અને 2F₂ની વચ્ચે
પ્રતિબિંબનો પ્રકારઃ વાસ્તવિક અને ઊલટું
પ્રતિબિંબનું પરિમાણ વસ્તુ કરતાં નાનું

(3) વસ્તુનું સ્થાન 2F₁ પર

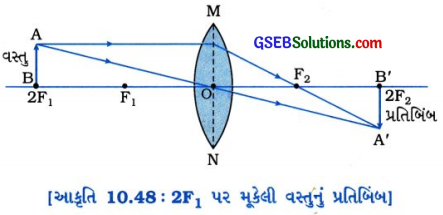
પ્રતિબિંબ પ્રતિબિંબનું સ્થાનઃ વસ્તુની વિરુદ્ધ બાજુએ 2F₂ પર
પ્રતિબિંબનો પ્રકારઃ વાસ્તવિક અને ઊલટું
પ્રતિબિંબનું પરિમાણ વસ્તુના પરિમાણ જેટલું

(4) વસ્તુનું સ્થાન: F₁ અને 2F₁ ની વચ્ચે

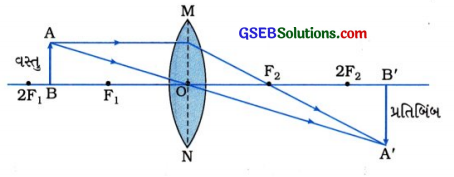
[આકૃતિ 10.49: F1 અને 2F ની વચ્ચે મૂકેલી વસ્તુનું પ્રતિબિંબ
પ્રતિબિંબનું સ્થાનઃ વસ્તુની વિરુદ્ધ બાજુએ 2F₂થી દૂર
પ્રતિબિંબનો પ્રકારઃ વાસ્તવિક અને ઊલટું
પ્રતિબિંબનું પરિમાણ વસ્તુથી મોટું (વિવર્ધિત)

(5) વસ્તુનું સ્થાન મુખ્ય કેન્દ્ર F₁ પર

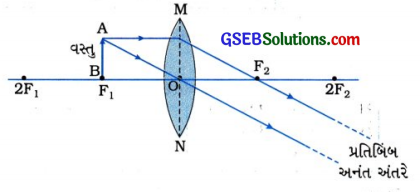
[આકૃતિ 10.50 મુખ્ય કેન્દ્ર F₁ પર મૂકેલી વસ્તુનું પ્રતિબિંબ]
પ્રતિબિંબનું સ્થાન અનંત અંતરે
પ્રતિબિંબનો પ્રકારઃ વાસ્તવિક અને ઊલટું
પ્રતિબિંબનું પરિમાણ વસ્તુથી અત્યંત મોટું (વિવર્ધિત)

(6) વસ્તુનું સ્થાનઃ F₁ અને O ની વચ્ચે

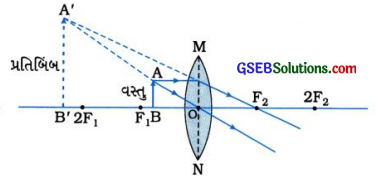
[આકૃતિ 10.51: F₁ અને oની વચ્ચે મૂકેલી વસ્તુનું પ્રતિબિંબ]
પ્રતિબિંબનું સ્થાન લેન્સની વસ્તુ તરફની બાજુએ અને વસ્તુઅંતરથી વધુ દૂર અંતરે
પ્રતિબિંબનો પ્રકાર: આભાસી અને ચતું
પ્રતિબિંબનું પરિમાણ વસ્તુથી મોટું (વિવર્ધિત)
[નોંધ: પ્રતિબિંબ આભાસી હોવાથી તૂટક રેખા વડે દર્શાવેલ છે.]

પ્રશ્ન 38.
અનંત અંતરે રહેલી વસ્તુનું અંતર્ગોળ લેન્સ વડે રચાતા પ્રતિબિંબનું સ્થાન, પ્રકાર અને પરિમાણ દર્શાવતી કિરણાકૃતિ દોરો.
ઉત્તર:
વસ્તુનું સ્થાન અનંત અંતરે

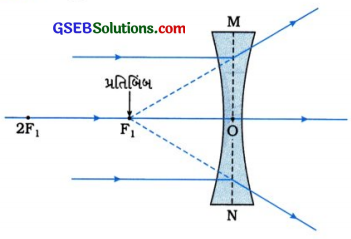
[આકૃતિ 10.52: અનંત અંતરે રહેલી વસ્તુનું પ્રતિબિંબ
પ્રતિબિંબનું સ્થાન લેન્સની વસ્તુ તરફની બાજુએ મુખ્ય કેન્દ્ર F₁ પર
પ્રતિબિંબનો પ્રકાર : આભાસી અને ચતું
પ્રતિબિંબનું પરિમાણ વસ્તુ કરતાં અત્યંત નાનું બિંદુવત્

પ્રશ્ન 39.
અનંત અંતર અને અંતર્ગોળ લેન્સના પ્રકાશીય કેન્દ્રની વચ્ચે ગમે ત્યાં મૂકેલી વસ્તુ માટે રચાતા પ્રતિબિંબનું સ્થાન, પ્રકાર અને પરિમાણ દર્શાવતી કિરણાકૃતિ દોરો.
ઉત્તર:
વસ્તુનું સ્થાનઃ અનંત અંતર અને પ્રકાશીય કેન્દ્ર (O)ની વચ્ચે ગમે ત્યાં.

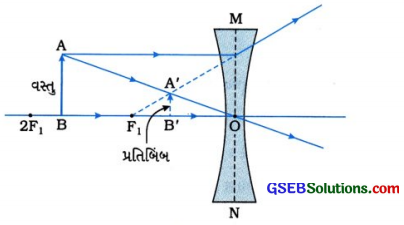
[આકૃતિ 10.53: અનંત અંતર અને 0 વચ્ચે મૂકેલી વસ્તુનું પ્રતિબિંબ].

પ્રતિબિંબનું સ્થાન લેન્સની વસ્તુ તરફની બાજુએ, F₁ અને = 0 ની વચ્ચે
પ્રતિબિંબનો પ્રકાર: આભાસી અને ચતું
પ્રતિબિંબનું પરિમાણ વસ્તુ કરતાં નાનું
[નોંધ: પ્રતિબિંબ આભાસી હોવાથી તૂટક રેખા વડે દર્શાવેલ છે.]
યાદ રાખો: અંતર્ગોળ લેન્સ વડે રચાતું પ્રતિબિંબ હંમેશાં આભાસી, ચતું અને નાનું હોય છે. આ પ્રતિબિંબ હંમેશાં લેન્સના પ્રકાશીય કેન્દ્ર (O) અને મુખ્ય કેન્દ્ર F_{1</sub. ની વચ્ચે હોય છે.}

પ્રશ્ન 40.
લેન્સ માટે સંજ્ઞા પ્રણાલી જણાવો.
ઉત્તર:
ગોલીય લેન્સ માટે સંજ્ઞા પ્રણાલી નીચે મુજબ છે :
લેન્સના પ્રકાશીય કેન્દ્ર (O)ને ઊગમબિંદુ તરીકે અને લેન્સના મુખ્ય અક્ષને યામ-પદ્ધતિના X-અક્ષ તરીકે લેવામાં આવે છે. Y-અક્ષ પ્રકાશીય કેન્દ્ર (O)માંથી પસાર થતો અને આકૃતિના સમતલમાં આવેલો છે.

1. વસ્તુને હંમેશાં લેન્સની ડાબી બાજુ (ગોલીય અરીસાની જેમ) મૂકવામાં આવે છે. એટલે કે વસ્તુમાંથી આવતાં પ્રકાશનાં કિરણો લેન્સ પર ડાબી બાજુથી આપાત થાય છે.
2. બધાં જ અંતરો લેન્સના પ્રકાશીય કેન્દ્ર (O)થી મુખ્ય 3 અક્ષને સમાંતર માપવામાં આવે છે.
3. આપાતકિરણની દિશામાં માપવામાં આવતાં અંતરો ધન 3 અને આપાતકિરણની વિરુદ્ધ દિશામાં માપવામાં આવતાં અંતરો ત્રણ લેવામાં આવે છે.
4. લેન્સના મુખ્ય અને લંબરૂપે ઉપરની તરફ માપેલ ઊંચાઈ ધન અને મુખ્ય અક્ષને લંબરૂપે નીચેની તરફ માપેલ ઊંચાઈ ઋણ લેવામાં આવે છે.

નોંધઃ સંજ્ઞા પ્રણાલી પ્રમાણે બહિર્ગોળ લેન્સની કેન્દ્રલંબાઈ ધન છે અને અંતર્ગોળ લેન્સની કેન્દ્રલંબાઈ કણ છે.]
બહિર્ગોળ લેન્સ માટે સંજ્ઞા પ્રણાલી:

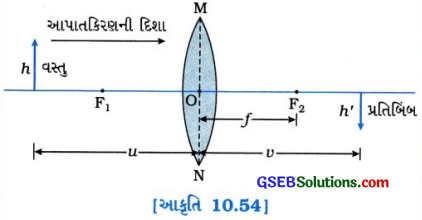
વસ્તુ-અંતર =-u
વાસ્તવિક પ્રતિબિંબ માટે પ્રતિબિંબ-અંતર = +v
કેન્દ્રલંબાઈ = +f
વસ્તુ-ઊંચાઈ = + h
વાસ્તવિક પ્રતિબિંબ માટે પ્રતિબિંબ-ઊંચાઈ = -h’
[નોંધ : આભાસી પ્રતિબિંબ માટે પ્રતિબિંબ-અંતર =અને પ્રતિબિંબ-ઊંચાઈ = + h’ લેવી.)

અંતર્ગોળ લેન્સ માટે સંજ્ઞા પ્રણાલી:

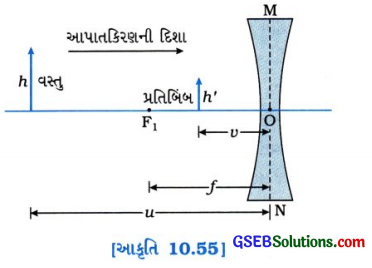
વસ્તુ-અંતર = – u
પ્રતિબિંબ-અંતર = -v
કેન્દ્રલંબાઈ = -f
વસ્તુ-ઊંચાઈ = + h
પ્રતિબિંબ-ઊંચાઈ = + h’

પ્રશ્ન 41.
લેન્સનું સૂત્ર એટલે શું? પાતળા અને નાના મુખવાળા લેન્સનું સૂત્ર જણાવો.
ઉત્તર:
પાતળા અને નાના મુખવાળા લેન્સ માટે વસ્તુ-અંતર u, પ્રતિબિંબ-અંતર છે અને કેન્દ્રલંબાઈ f વચ્ચેનો સંબંધ દર્શાવતા સમીકરણને લેન્સનું સૂત્ર (અથવા લેન્સ-સૂત્રો કહે છે.
પાતળા અને નાના મુખવાળા લેન્સનું સૂત્ર \(\frac{1}{v}\) – \(\frac{1}{u}\) = \(\frac{1}{f}\) છે.
[નોંધઃ લેન્સનું સૂત્ર બધાં વસ્તુ-અંતરો અને દરેક લેન્સ માટે સાચું છે.]

પ્રશ્ન 42.
લેન્સ દ્વારા મળતી મોટવણીની વ્યાખ્યા આપો. તેને ટૂંકમાં સમજાવો.
ઉત્તર:
લેન્સ દ્વારા મળતા પ્રતિબિંબની ઊંચાઈ અને વસ્તુની ઊંચાઈના ગુણોત્તરને પ્રતિબિંબની મોટવણી કહે છે.

• મોટવણીને m વડે દર્શાવાય છે.
• જો વસ્તુની ઊંચાઈ h હોય અને લેન્સ વડે મળતા પ્રતિબિંબની ઊંચાઈ h’ હોય, તો લેન્સ દ્વારા મળતી મોટવણી,
  
• લેન્સની મોટવણી વસ્તુ-અંતર (u) અને પ્રતિબિંબ-અંતર (D) સાથે સંબંધિત છે. આ સંબંધ નીચે મુજબ છેઃ મોટવણી m = \(\frac{h^{\prime}}{h}\) = \(\frac{v}{u}\) …… (10.17)

પ્રશ્ન 43.
ગોલીય લેન્સની મોટવણી માટેનું સૂત્ર m = \(\frac{v}{u}\) મેળવો.
ઉત્તર :

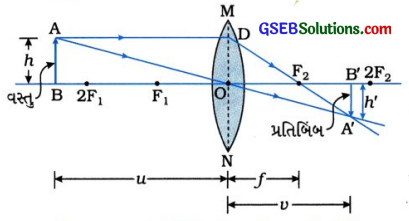
[આકૃતિ 10.56: બહિર્ગોળ લેન્સ વડે રચાતું પ્રતિબિંબ]

• ગોલીય લેન્સ વડે મળતા પ્રતિબિંબની મોટવણી
  

હવે, આકૃતિ 10.56 પરથી સ્પષ્ટ છે કે કાટકોણ ત્રિકોણો ABO અને A’B’O સમરૂપ છે.
∴ \(\frac{\mathrm{AB}}{\mathrm{A}^{\prime} \mathrm{B}^{\prime}}\) = \(\frac{\mathrm{OB}}{\mathrm{OB}^{\prime}}\)

• અહીં નવી કાર્તેઝિયન સંજ્ઞા પ્રણાલી અનુસાર,

AB = +h
A’B’ =- h’
OB = – u
OB’ = + v

પ્રશ્ન 44.
લેન્સના પાવર વિશે નોંધ લખો.
અથવા
લેન્સના પાવરની વ્યાખ્યા લખો. તેનો sx એકમ જણાવો. પાવર માપવા માટે વપરાતા સાધનનું નામ જણાવો.
ઉત્તર:
લેન્સની કેન્દ્રલંબાઈ (f)ના વ્યસ્તને લેન્સનો પાવર (P) કહે છે.

• બહિર્ગોળ લેન્સના મુખ્ય અક્ષને સમાંતર આપાત થતાં પ્રકાશનાં કિરણો લેન્સ વડે વક્રીભવન પામી મુખ્ય કેન્દ્ર F₂ આગળ કેન્દ્રિત થાય છે.
• અંતગોંળ લેન્સના મુખ્ય અક્ષને સમાંતર આપાત થતાં પ્રકાશનાં કિરણો લેન્સ વડે વક્રીભવન પામી મુખ્ય કેન્દ્ર F₁માંથી વિકેન્દ્રિત થતા હોય તેવો ભાસ થાય છે.
  લેન્સની પ્રકાશનાં કિરણોને કેન્દ્રિત કે વિકેન્દ્રિત કરવાની ક્ષમતા તેની કેન્દ્રલંબાઈ ઉપર આધાર રાખે છે.
  લેન્સની કેન્દ્રલંબાઈ જેમ ઓછી તેમ પ્રકાશનાં કિરણોને કેન્દ્રિત – કે વિકેન્દ્રિત કરવાની ક્ષમતા વધારે.
• લેન્સની પ્રકાશનાં સમાંતર કિરણોને કેન્દ્રિત કે વિકેન્દ્રિત કરવાની ક્ષમતા લેન્સના પાવર સ્વરૂપે રજૂ કરવામાં આવે છે. તેથી જ લેન્સના પાવરની વ્યાખ્યા તેની કેન્દ્રલંબાઈના વ્યસ્ત વડે આપવામાં આવે છે.
  ∴ લેન્સનો પાવર P = \(\frac{1}{f}\) ….. (10.18)
• લેન્સના પાવરનો SI એકમ ડાયોપ્ટર છે. તેને D વડે દર્શાવાય છે.
• જો કેન્દ્રલંબાઈ 5 મીટરમાં હોય, તો ID = 1m^-1.
  આમ, 1 ડાયોપ્ટર એટલે 1 મીટર કેન્દ્રલંબાઈવાળા લેન્સનો પાવર.
• નવી કાર્તેઝિયન સંજ્ઞા પ્રણાલી અનુસાર બહિર્ગોળ લેન્સનો પાવર ધન (∵ તેની 7 ધન) અને અંતર્ગોળ લેન્સનો પાવર ણ (∵ તેની f ઋણ) હોય છે.
• ઑપ્ટિશિયન અથવા આંખના ડૉક્ટર, આંખ તપાસી ચશ્માંનાં જે નંબર પ્રિસ્ક્રિપ્શનમાં લખી આપે છે, તે હકીકતમાં શુદ્ધિકારક લેન્સનો પાવર જ છે.
• ચશ્માંના કાચનો / લેન્સનો પાવર P = +2.0 D છે. તેનો અર્થ તે f = \(\frac{1}{P}\) = \(\frac{1}{2}\) = 0.5 m કેન્દ્રલંબાઈવાળો બહિર્ગોળ લેન્સ છે.
• ચશ્માંના કાચનો / લેન્સનો પાવર P = -2.5 D છે. તેનો અર્થ તે f = \(\frac{1}{P}\) = \(\frac{1}{-2.5}\) = -0.4m કેન્દ્રલંબાઈવાળો અંતર્ગોળ લેન્સ છે.
• લેન્સનો પાવર માપવા માટે વપરાતા સાધનને ડાયોપ્ટર મિટર કહે છે.

નોંધઃ

1. ટૂંકી કેન્દ્રલંબાઈવાળો બહિર્ગોળ લેન્સ, પ્રકાશનાં કિરણોને મોટા ખૂણે વાંકાં વાળે છે અને તેમને પ્રકાશીય કેન્દ્રની નજીક કેન્દ્રિત કરે છે.
2. ટૂંકી કેન્દ્રલંબાઈવાળો અંતર્ગોળ લેન્સ મોટી કેન્દ્રલંબાઈવાળા અંતર્ગોળ લેન્સ કરતાં વધારે અપસરણ ઉપજાવે છે.

હેતુલક્ષી પ્રશ્નોત્તરી

પ્રશ્ન 1.
નીચેના પ્રશ્નોના ઉત્તર એક શબ્દ વાક્યમાં આપોઃ

પ્રશ્ન 1.
બહિર્ગોળ અરીસા વડે વિવર્ધિત પ્રતિબિંબ મેળવી શકાય? હા કે ના જણાવો.
ઉત્તર:
ના

પ્રશ્ન 2.
અરીસા પર જ્યારે પ્રકાશકિરણ લંબરૂપે આપાત થાય છે ત્યારે પરાવર્તિતકોણ કેટલો હશે?
ઉત્તર:
0°

પ્રશ્ન 3.
કિરણાકૃતિમાં ગોલીય અરીસા પરના કોઈ બિંદુ A પાસે તમે લંબ કેવી રીતે દોરશો?
ઉત્તર:
અરીસા પરના બિંદુ મને તેના વક્રતાકેન્દ્ર C સાથે જોડતી રેખા ઘેરીને

પ્રશ્ન 4.
ગોલીય અરીસાની કેન્દ્રલંબાઈ શોધવા માટેનું સૂત્ર લખો.
ઉત્તર:
\(\frac{1}{f}\) = \(\frac{1}{u}\) + \(\frac{1}{v}\)

પ્રશ્ન 5.
બહિર્ગોળ અરીસાની કેન્દ્રલંબાઈ 15cm છે, તો તેની વક્રતાત્રિજ્યા છે કેટલી હશે?
ઉત્તર:
R = 30 cm

પ્રશ્ન 6.
જ્યારે પ્રકાશનું કિરણ એક માધ્યમમાંથી બીજા માધ્યમમાં જાય છે, ત્યારે તેની કઈ બે રાશિઓમાં ફેરફાર થાય છે?
ઉત્તર:
તરંગલંબાઈ અને વેગ

પ્રશ્ન 7.
અંતર્ગોળ લેન્સની મોટવણી હંમેશાં 1 કરતાં ઓછી હોય છે. કેમ?
ઉત્તર:
વસ્તુના કોઈ પણ સ્થાન માટે અંતર્ગોળ લેન્સ વડે રચાતું પ્રતિબિંબ હંમેશાં નાનું હોય છે.

પ્રશ્ન 8.
શું માધ્યમનો વક્રીભવનાંક તેમાંથી પસાર થતા પ્રકાશની આવૃત્તિ પર આધાર રાખે છે?
ઉત્તર:
ના, n = \(\frac{c}{v}\) = \(\frac{f \lambda}{f \lambda^{\prime}}\) = \(\frac{\lambda}{\lambda^{\prime}}\) પરથી.
(∵ આવૃત્તિ f = અચળ)

પ્રશ્ન 9.
કયા અરીસાનો દશ્ય-વિસ્તાર મોટો હોય છે?
ઉત્તર:
બહિર્ગોળ

પ્રશ્ન 10.
કાર્બન ડાયસલ્ફાઇડનો નિરપેક્ષ વક્રીભવનાંક 1.63 છે, તો હું પ્રકાશના વેગના સંદર્ભમાં આ વિધાનનું અર્થઘટન કરો.
ઉત્તર:
n = \(\frac{c}{v}\) પરથી,

કાર્બન ડાયસલ્ફાઇડમાં પ્રકાશનો વેગ 1.84 × 10⁸ ms^-1 હશે.

પ્રશ્ન 11.
અંતર્ગોળ અરીસાની સામે મુખ્ય અક્ષ પરનાં કયાં બે બિંદુઓ વચ્ચે વસ્તુને મૂકવી જોઈએ, જેથી તેના પ્રતિબિંબની મોટવણી m = -3 મળે?
ઉત્તર:
અહીં, m = -3 છે. તેથી પ્રતિબિંબ સાચું, ઊલટું અને વિવર્ધિત હશે. તેથી વસ્તુને F અને Cની વચ્ચે મૂકવી જોઈએ.

પ્રશ્ન 12.
અરીસો એટલે શું?
ઉત્તર:
અરીસો એટલે લીસી અને ચકચકિત સપાટી, જે તેના પર આપાત પ્રકાશનું મોટા ભાગે (આશરે 95%) પરાવર્તન કરે.

પ્રશ્ન 13.
મેગ્નિફાઇંગ લેન્સ (વિવર્ધિત લેન્સ) તરીકે કયો લેન્સ વાપરવામાં આવે છે?
ઉત્તર:
બહિર્ગોળ લેન્સ

પ્રશ્ન 14.
એક મીણબત્તી સમતલ અરીસાથી 20 cm અંતરે મૂકેલી છે, તો મીણબત્તી અને મીણબત્તીના પ્રતિબિંબ વચ્ચે કેટલું અંતર હશે?
ઉત્તર:
40 cm

પ્રશ્ન 2.
ખાલી જગ્યા પૂરોઃ

પ્રશ્ન 1.
ગોલીય અરીસાના મધ્યબિંદુને ……… અને લેન્સના મધ્યબિંદુને ……… કહેવામાં આવે છે.
ઉત્તર:
ધ્રુવ, પ્રકાશીય કેન્દ્ર

પ્રશ્ન 2.
10 cm કેન્દ્રલંબાઈવાળા બહિર્ગોળ લેન્સનો પાવર …….. D છે.
ઉત્તર:
10

પ્રશ્ન 3.
જ્યારે પ્રકાશનું કિરણ પાણીમાંથી ગતિ કરીને હવામાં દાખલ થાય છે ત્યારે તેની ઝડપ ………..
ઉત્તર:
વધે છે.

પ્રશ્ન 4.
બહિર્ગોળ લેન્સની કેન્દ્રલંબાઈ ………… હોય છે.
ઉત્તર:
ધન

પ્રશ્ન 5.
………… પ્રતિબિંબો પડદા પર મેળવી શકાય છે.
ઉત્તર:
વાસ્તવિક

પ્રશ્ન 6.
ગોલીય અરીસા વડે મળતી પ્રતિબિંબની મોટવણી ધન છે. તેથી પ્રતિબિંબનો પ્રકાર ……….. હશે.
ઉત્તર:
ચતું અને આભાસી

પ્રશ્ન 7.
લેન્સ વડે મળતી પ્રતિબિંબની મોટવણી ઋણ છે. તેથી પ્રતિબિંબ ………. અને ……….. હશે.
ઉત્તર:
ઊલટું, વાસ્તવિક

પ્રશ્ન 8.
સમતલ અરીસા પર અરીસાની સપાટી સાથે 30°ના ખૂણે એક પ્રકાશકિરણ આપાત થાય છે, તો આપાતકિરણ અને પરાવર્તિતકિરણ વચ્ચેનો ખૂણો ……… હશે.
ઉત્તર:
120°

પ્રશ્ન 9.
બહિર્ગોળ લેન્સ વડે વસ્તુનું આભાસી, ચતું અને વિવર્ધિત પ્રતિબિંબ મળે છે; તો વસ્તુને ………. અંતરે મૂકી હશે.
ઉત્તર:
પ્રકાશીય કેન્દ્રથી કેન્દ્રલંબાઈ કરતાં ઓછા

પ્રશ્ન 10.
અરીસા અથવા લેન્સના કિસ્સામાં પ્રતિબિંબની ઊંચાઈ અને વસ્તુની ઊંચાઈના ગુણોત્તરને ………. કહે છે.
ઉત્તર:
મોટવણી

પ્રશ્ન 11.
…………… લેન્સ તેના મધ્યભાગ કરતાં ધાર પાસે વધારે જાડો હોય છે.
ઉત્તર:
અંતર્ગોળ

પ્રશ્ન 12.
ENT સ્પેશિયાલિસ્ટ ડૉક્ટર નાના દર્પણમુખવાળા ……….. નો ઉપયોગ કરે છે.
ઉત્તર:
અંતર્ગોળ અરીસા

પ્રશ્ન 13.
મેગ્નિફાઇંગ કાચ તરીકે ………. નો ઉપયોગ કરવામાં આવે છે.
ઉત્તર:
બહિર્ગોળ લેન્સ

પ્રશ્ન 14.
ચશ્માંની બનાવટમાં વપરાયેલ શુદ્ધિકારક લેન્સનો પાવર -0.4 D છે, તો તે લેન્સનો પ્રકાર ………. હશે.
ઉત્તર:
અંતર્ગોળ

પ્રશ્ન 15.
લેન્સનો પાવર માપવા માટે વપરાતા સાધનનું નામ ………. છે.
ઉત્તર :
ડાયોપ્ટર મિટર

પ્રશ્ન 3.
નીચેના વિધાનો ખરાં છે કે ખોટાં તે જણાવો:

પ્રશ્ન 1.
આભાસી પ્રતિબિંબ પડદા પર મેળવી શકાય છે.
ઉત્તરઃ
ખોટું

પ્રશ્ન 2.
અનિયમિત પરાવર્તનના કિસ્સામાં પરાવર્તિત પ્રકાશનું કિરણપુંજ ચોક્કસ દિશામાં સમાંતર હોય છે.
ઉત્તરઃ
ખોટું

પ્રશ્ન 3.
કોઈ પણ પ્રકારના અરીસા માટે પરાવર્તનના નિયમો પળાય છે.
ઉત્તરઃ
ખરું

પ્રશ્ન 4.
પરાવર્તનના નિયમો ખરબચડી અને અનિયમિત સપાટીને લાગુ પાડી શકાય નહીં.
ઉત્તરઃ
ખોટું

પ્રશ્ન 5.
ગોલીય અરીસાની પરાવર્તક સપાટીના વ્યાસને અરીસાનું દર્પણમુખ કહે છે.
ઉત્તરઃ
ખરું

પ્રશ્ન 6.
અરીસા વડે રચાતા પ્રતિબિંબનું સ્થાન મેળવવા માટે ઓછામાં ઓછાં ચાર કિરણોની જરૂર પડે છે.
ઉત્તરઃ
ખોટું

પ્રશ્ન 7.
અંતર્ગોળ અરીસાથી વસ્તુને અનંત અંતરે મૂકવામાં આવે, તો પ્રતિબિંબ વક્રતાકેન્દ્ર પર રચાય છે.
ઉત્તરઃ
ખોટું

પ્રશ્ન 8.
પાણી કરતાં હવા વધારે પ્રકાશીય ઘટ્ટ માધ્યમ છે.
ઉત્તરઃ
ખોટું

પ્રશ્ન 9.
જ્યારે પ્રકાશનું કિરણ પ્રકાશીય ઘટ્ટ માધ્યમમાંથી પ્રકાશીય પાતળા માધ્યમમાં જાય ત્યારે તેનો વેગ ઘટે છે.
ઉત્તરઃ
ખોટું

પ્રશ્ન 10.
કાચના પાતળા લેન્સનો મધ્યભાગ કાચના લંબઘન સ્લેબની માફક વર્તે છે.
ઉત્તરઃ
ખરું

પ્રશ્ન 11.
દરેક અરીસા અને લેન્સ માટે નવી કાર્તેઝિયન સંજ્ઞા પ્રણાલી મુજબ વસ્તુ-અંતર ‘u ઋણ લેવામાં આવે છે.
ઉત્તરઃ
ખરું

પ્રશ્ન 12.
અરીસા માટે m = \(\frac{v}{u}\) અને લેન્સ માટે m = –\(\frac{v}{u}\) છે.
ઉત્તરઃ
ખોટું

પ્રશ્ન 13.
એક લેન્સનો પાવર P = 5D છે. તેથી તેની કેન્દ્રલંબાઈ f = 0.2 cm છે.
ઉત્તરઃ
ખોટું

પ્રશ્ન 14.
જ્યારે પ્રકાશનું કિરણ શૂન્યાવકાશમાંથી કોઈ પારદર્શક માધ્યમમાં દાખલ થાય છે, ત્યારે આપાતબિંદુ આગળ દોરેલા લંબથી દૂર તરફ વિચલિત થાય છે.
ઉત્તરઃ
ખોટું

પ્રશ્ન 15.
જે માધ્યમની દળ ઘનતા વધુ હોય છે, તે હંમેશાં વધારે પ્રકાશીય ઘટ્ટ માધ્યમ હોય છે.
ઉત્તરઃ
ખોટું

પ્રશ્ન 4.
જોડકાં જોડો :

પ્રશ્ન 1.

ઉત્તર:
(1 – s),
(2 – t),
(3 – q),
(4 – p).

પ્રશ્ન 2.

ઉત્તર:
(1 – p),
(2 – r),
(3 – q),
(4 – s).

પ્રશ્ન 5.
નીચેના દરેક પ્રશ્નના ઉત્તર માટે આપેલા વિકલ્પોમાંથી સાચો વિકલ્પ પસંદ કરો :

પ્રશ્ન 1.
દશ્યપ્રકાશની તરંગલંબાઈનો વિસ્તાર કેટલો છે?
A. 4 × 10^-7m થી 8 × 10^-7 m
B. 4 × 10^-9 m થી 8 × 10^-9 m
C. 4 × 10^-5 m થી 8 × 10^-5 m
D. 4 × 10^-6 m થી 8 × 10^-6 m
ઉત્તર:
4 × 10^-7m થી 8 × 10^-7 m

પ્રશ્ન 2.
ગોલીય અરીસા માટે વક્રતા ત્રિજ્યા (R) અને કેન્દ્રલંબાઈ (f) વચ્ચે શો સંબંધ છે?
A. R = f / 2
B. R = f
C. R = 2f
D. R = 3f
ઉત્તર:
R = 2f

પ્રશ્ન ૩.
વક્રતાકેન્દ્ર (C)માંથી પસાર થતું પ્રકાશનું કિરણ અંતર્ગોળ અરીસા પરથી પરાવર્તન પામી કયા બિંદુમાંથી પસાર થશે?
A. મુખ્ય કેન્દ્ર
B. વક્રતાકેન્દ્ર
C. ધ્રુવ
D. આપેલ તમામ
ઉત્તર:
વક્રતાકેન્દ્ર

પ્રશ્ન 4.
અંતર્ગોળ અરીસાની સામે વસ્તુને કયા સ્થાને મૂકતાં તેનું આભાસી અને ચતું પ્રતિબિંબ રચાય?
A. મુખ્ય કેન્દ્ર (F) પર
B. વક્રતાકેન્દ્ર (C) પર
C. મુખ્ય કેન્દ્ર અને ધૃવની વચ્ચે
D. વક્રતાકેન્દ્રથી દૂર
ઉત્તર:
મુખ્ય કેન્દ્ર અને ધૃવની વચ્ચે

પ્રશ્ન 5.
સમતલ અરીસાની મોટવણીનું મૂલ્ય હંમેશાં ……… હોય.
A. 1 કરતાં વધુ
B. 1
C. 1 કરતાં ઓછું
D. શૂન્ય
ઉત્તર:
1

પ્રશ્ન 6.
સમતલ અરીસાની કેન્દ્રલંબાઈ હોય.
A. શૂન્ય
B. અનંત
C. વસ્તુ-અંતર કરતાં અડધી
D. વસ્તુ-અંતર જેટલી
ઉત્તર:
અનંત

પ્રશ્ન 7.
સમતલ અરીસા વડે 2m દૂર રહેલી વસ્તુ અને તેના પ્રતિબિંબ વચ્ચે કેટલું અંતર હોય?
A. 4 m
B. 1 m
C. 2 m
D. 3m
Hint: વસ્તુ અને તેના પ્રતિબિંબ વચ્ચેનું અંતર
= | u | + | v |
= 2 + 2 (∵ અહીં, | u | = | v |)
= 4m
ઉત્તર:
4 m

પ્રશ્ન 8.
વસ્તુને કયા સ્થાને મૂકવાથી બહિર્ગોળ લેન્સ વડે વસ્તુનું વાસ્તવિક, ઊલટું અને તેના જેટલી જ ઊંચાઈનું પ્રતિબિંબ મળે?
A. મુખ્ય કેન્દ્ર (F₁) પર
B. મુખ્ય કેન્દ્ર (F₁) અને 2F₁ ની વચ્ચે
C. 2F₁ પર
D. મુખ્ય કેન્દ્ર (F₁) અને પ્રકાશીય કેન્દ્ર (O)ની વચ્ચે
ઉત્તર:
2F₁ પર

પ્રશ્ન 9.
નીચેનામાંથી કયા દ્રવ્યની પ્રકાશીય ઘનતા સૌથી વધુ છે?
A. કાચ
B. પાણી
C. કાર્બન ડાયસલ્ફાઈડ
D. હીરો
Hint: આપેલ દ્રવ્યોમાંથી હીરાનો નિરપેક્ષ વક્રીભવનાંક સૌથી વધુ છે.
ઉત્તર:
હીરો

પ્રશ્ન 10.
કોઈ પણ માધ્યમનો નિરપેક્ષ વક્રીભવનાંક હંમેશાં ……… હોય છે.
A. 1
B. > 1
C. < 1
D. 0
ઉત્તર:
> 1

પ્રશ્ન 11.
10 cm, 20 cm, 25 cm અને 50 cm કેન્દ્રલંબાઈ ધરાવતા લેન્સ પૈકી કયા લેન્સનો પાવર સૌથી વધુ હોય છે?
A. 50 cm
B. 25 cm
C. 20 cm
D. 10 cm
Hint: પાવર P = \(\frac{1}{f}\) પરથી જે લેન્સની કેન્દ્રલંબાઈ f ઓછી હશે, તેનો પાવર P વધુ હશે.
ઉત્તર:
10 cm

પ્રશ્ન 12.
બહિર્ગોળ લેન્સનો પાવર +5.0D હોય, તો તેની કેન્દ્રલંબાઈ કેટલી થાય?
A. – 10 cm
B. – 20 cm
C. + 10 cm
D. + 20 cm
Hint : P = \(\frac{1}{f}\)
∴ f = \(\frac{1}{P}\) = \(\frac{1}{5}\) = 0.2 m = + 20 cm
ઉત્તર:
+20 cm

પ્રશ્ન 13.
જો પાણી, બેન્જિન અને નીલમના વક્રીભવનાંક અનુક્રમે 1.33, 1.50 અને 1.77 હોય, તો કયા માધ્યમનો સાપેક્ષ વક્રીભવનાંક સૌથી વધુ હોય?
A. નીલમનો પાણીની સાપેક્ષ
B. નીલમનો બેઝિનની સાપેક્ષ
C. બેન્ઝિનનો પાણીની સાપેક્ષ
D. પાણીનો બેન્ઝિનની સાપેક્ષ
Hint: પાણીને માધ્યમ 1, બેન્ઝિનને માધ્યમ 2 અને નીલમને માધ્યમ 3 તરીકે લેતાં,

∴ નીલમનો પાણીની સાપેક્ષે વક્રીભવનાંક વધુ હશે.
ઉત્તર:
નીલમનો પાણીની સાપેક્ષ

પ્રશ્ન 14.
સમતલ અરીસા વડે કેવું પ્રતિબિંબ રચાય?
A. વાસ્તવિક અને ઊલટું
B. વાસ્તવિક અને ચતું
C. આભાસી અને ચતું
D. આભાસી અને ઊલટું
ઉત્તર:
આભાસી અને ચતું

પ્રશ્ન 15.
જો પાણી અને કાચના નિરપેક્ષ વક્રીભવનાંક અનુક્રમે \(\frac{4}{3}\) અને \(\frac{3}{2}\) હોય, તો પ્રકાશનો પાણી અને કાચમાં વેગનો ગુણોત્તર કેટલો હશે? A. 2
B. \(\frac{8}{9}\).
C. \(\frac{9}{8}\)
D. \(\frac{1}{2}\)
Hint: પાણી અને કાચને અનુક્રમે માધ્યમ 1 અને માધ્યમ 2 તરીકે લેતાં, પ્રકાશનો પાણીમાં વેગ, અને કાચમાં વેગ ઈઝ થાય. અહીં, n₁ = \(\frac{4}{3}\) અને n₂ = \(\frac{3}{2}\) છે.

ઉત્તર:
\(\frac{9}{8}\)

પ્રશ્ન 16.
પાણી, કાચ અને હીરાના નિરપેક્ષ વક્રીભવનાંક અનુક્રમે 1.33, 1.50 અને 2.42 છે, તો કયું માધ્યમ સૌથી વધુ પ્રકાશીય ઘટ્ટ હશે?
A. પાણી
B.
C. હીરો
D. આપેલ પૈકી એક પણ નહિ
Hint: જે માધ્યમનો નિરપેક્ષ વક્રીભવનાંક વધુ હોય તે વધુ પ્રકાશીય ઘટ્ટ હોય છે.
ઉત્તર:
હીરો

પ્રશ્ન 17.
નીચેનામાંથી શાના વડે રચાતાં પ્રતિબિંબ હંમેશાં આભાસી હોય છે?
A. અંતર્ગોળ અરીસા અને બહિર્ગોળ લેન્સ
B. બહિર્ગોળ અરીસા અને અંતર્ગોળ લેન્સ
C. બહિર્ગોળ અરીસા અને બહિર્ગોળ લેન્સ
D. અંતર્ગોળ અરીસા અને અંતર્ગોળ લેન્સ
ઉત્તર:
બહિર્ગોળ અરીસા અને અંતર્ગોળ લેન્સ

પ્રશ્ન 18.
માધ્યમની સપાટીને લંબરૂપે આપાત થતા પ્રકાશના કિરણનો વક્રીભૂતકોણ કેટલો હોય?
A. 90°
B. 60°
C. 30°
D. 0°
Hint: સ્નેલના નિયમ પરથી,
n₁ sin i = n₂ sin r. તે પરથી, જો i = 0° હોય, તો r = 0° થાય. કારણ કે,
n₁ અને n₂નાં મૂલ્ય શૂન્ય હોતાં નથી.
ઉત્તર:
૦°

પ્રશ્ન 19.
અરીસાની સામે તમે તેનાથી કોઈ પણ અંતરે ઊભા રહો તમારું પ્રતિબિંબ હંમેશાં ચતું મળે છે, તો અરીસો…
A. માત્ર સમતલ હશે.
B. માત્ર અંતર્ગોળ હશે.
C. માત્ર બહિર્ગોળ હશે.
D. સમતલ અથવા બહિર્ગોળ હશે.
ઉત્તર:
સમતલ અથવા બહિગળ હશે.

પ્રશ્ન 20.
અરીસા વડે વાસ્તવિક વસ્તુનું આભાસી પ્રતિબિંબ રચાય, તો…
A. તે બહિર્ગોળ હશે.
B. તે અંતગળ હશે.
C. તે સમતલ હશે.
D. ઉપરના આપેલ અરીસાઓ પૈકી કોઈ પણ હોઈ શકે.
ઉત્તર:
ઉપરના આપેલ અરીસાઓ પૈકી કોઈ પણ હોઈ શકે.

પ્રશ્ન 21.
એક વસ્તુને અંતર્ગોળ અરીસાના વક્રતાકેન્દ્ર પર મૂકેલ છે. આ વસ્તુના પ્રતિબિંબ અને અરીસાના ધ્રુવ વચ્ચેનું અંતર…
A. f જેટલું હશે.
B. 7 અને 25 વચ્ચેની લંબાઈ જેટલું હશે.
C. 25 જેટલું હશે.
D. 2 કરતાં વધુ હશે.
ઉત્તર:
27 જેટલું હશે.

પ્રશ્ન 22.
એક શાંત તળાવની પાણીની સમક્ષિતિજ સપાટી પર હવામાં ગતિ કરતું પ્રકાશનું ત્રાંસું કિરણ આપાત થાય છે. તળાવની અંદર પાણીમાં તે…
A. વિચલન પામ્યા વગર ગતિ કરશે.
B. તળાવની સપાટીના આપાતબિંદુએ દોરેલ લંબથી દૂર તરફ વિચલિત થશે.
C. તળાવની સપાટીના આપાતબિંદુએ દોરેલ લંબ તરફ વિચલિત થશે.
D. પોતાના મૂળ માર્ગે પાછું વળશે.
ઉત્તર:
તળાવની સપાટીના આપાતબિંદુએ દોરેલ લંબ તરફ વિચલિત થશે.

પ્રશ્ન 23.
નીચે દર્શાવેલ આકૃતિમાં પ્રકાશનું કિરણ માધ્યમ Aમાંથી ગતિ કરીને માધ્યમ 8માં દાખલ થાય છે, તો માધ્યમ Bનો માધ્યમ Aની સાપેક્ષે વક્રીભવનાંક ……. હશે.

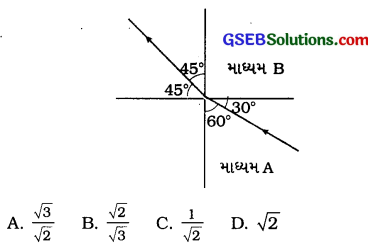
Hint: સ્નેલના નિયમ પરથી,
માધ્યમ Bનો માધ્યમ Aની સાપેક્ષે વક્રીભવનાંક

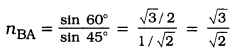
ઉત્તર:
\(\frac{\sqrt{3}}{\sqrt{2}}\)

પ્રશ્ન 24.
એક પ્રકાશનું કિરણ નીચે દર્શાવેલ આકૃતિ મુજબ માધ્યમ Aમાંથી માધ્યમ Bમાં દાખલ થાય છે, તો માધ્યમ Aનો માધ્યમ Bની સાપેક્ષે વક્રીભવનાંક ……… હશે.

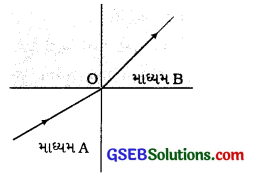
A. > 1
B. < 1
C. = 1
D. = 0
Hint: માધ્યમ Aમાં ગતિ કરતું પ્રકાશનું કિરણ માધ્યમ Bમાં દાખલ થાય છે ત્યારે આપાતબિંદુ પાસે દોરેલા લંબ તરફ વાંકું વળે છે. તેનો અર્થ માધ્યમ B, માધ્યમ તેની સાપેક્ષે વધુ પ્રકાશીય ઘટ્ટ માધ્યમ છે. તેથી માધ્યમ Bનો નિરપેક્ષ વક્રીભવનાંક માધ્યમ Aના નિરપેક્ષ વક્રીભવનાંક કરતાં વધુ હશે. તેથી માધ્યમ થનો માધ્યમ Bની સાપેક્ષે વક્રીભવનાંક n_AB = \(\frac{n_{\mathrm{A}}}{n_{\mathrm{B}}}\) < 1 થાય.
ઉત્તર:
< 1

પ્રશ્ન 25.
વાહનોમાં પાછળની વસ્તુઓ જોવા માટે લગાડેલ ‘સાઇડ ગ્લાસ વડે મળતી પ્રતિબિંબની મોટવણી m…
A. < 1 હોય છે.
B. = 1 હોય છે.
C. > 1હોય છે.
D. 1 કરતાં વધુ કે ઓછી હશે અને તેનો આધાર અરીસાથી વસ્તુના સ્થાન પર છે.
Hint: વાહનોમાં “સાઈડ ગ્લાસ’ તરીકે બહિર્ગોળ અરીસો વપરાય છે. તેના વડે રચાતું પ્રતિબિંબ હંમેશાં આભાસી અને નાનું મળે છે. તેથી મોટવણી < 1 હોય છે.
ઉત્તર:
< 1 હોય છે.

પ્રશ્ન 26.
A, B અને C ત્રણેય જુદાં જુદાં માધ્યમો છે. તેમના નિરપેક્ષ વક્રીભવનાંક અનુક્રમે 1.33, 1.65 અને 1.46 છે, તો કયા માધ્યમમાં પ્રકાશની ઝડપ સૌથી વધુ હશે?
A. માધ્યમ A
B. માધ્યમ B
C. માધ્યમ C
D. ત્રણેય માધ્યમોમાં એકસરખી હશે.
Hint: જે માધ્યમનો નિરપેક્ષ વક્રીભવનાંક ઓછો હોય તે ઓછું પ્રકાશીય ઘટ્ટ માધ્યમ હોય છે. ઓછા પ્રકાશીય ઘટ્ટ માધ્યમમાં પ્રકાશની ઝડપ વધુ હોય છે.
ઉત્તર:
માધ્યમ

પ્રશ્ન 27.
બહિર્ગોળ અરીસાની સામે મૂકેલ વસ્તુને મોટા અંતરથી, અરીસાના ધ્રુવ તરફ ગતિ કરાવવામાં આવે, તો પ્રતિબિંબનું કદ……
A. વધે છે.
B. ઘટે છે.
C. અચળ રહે છે.
D. પહેલાં વધે અને પછી ઘટે છે.
ઉત્તર:
વધે છે.

પ્રશ્ન 28.
બહિર્ગોળ અરીસાની સામે મૂકેલ વસ્તુને મોટા અંતરથી, અરીસાના ધ્રુવ તરફ ગતિ કરાવવામાં આવે, તો પ્રતિબિંબ…….
A. ધ્રુવ તરફ ખસે છે.
B. ધ્રુવથી દૂર તરફ ખસે છે.
C. પહેલાં ધ્રુવથી દૂર તરફ અને પછી ધ્રુવ તરફ ખસે છે.
D. પહેલાં ધ્રુવ તરફ અને પછી ધ્રુવથી દૂર તરફ ખસે છે.
ઉત્તર:
ધ્રુવ તરફ ખસે છે.

પ્રશ્ન 29.
ગોલીય અરીસાની સપાટીના મધ્યબિંદુને શું કહે છે?
A. મુખ્ય કેન્દ્ર
B. વક્રતાકેન્દ્ર
C. મુખ્ય અક્ષ
D. ધ્રુવ
ઉત્તર:
ધ્રુવ

પ્રશ્ન 30.
ગોલીય અરીસાની વર્તુળાકાર ધારના વ્યાસને શું કહે છે?
A. દર્પણમુખ
B. વક્રતાત્રિજ્યા
C. કેન્દ્રલંબાઈ
D. મુખ્ય અક્ષ
ઉત્તર:
દર્પણમુખ

પ્રશ્ન 31.
અંતર્ગોળ અરીસાની મદદથી વસ્તુનું વાસ્તવિક અને વસ્તુના કદ જેટલું પ્રતિબિંબ મેળવવા વસ્તુને ક્યાં મૂકવી જોઈએ?
A. અનંત અંતરે
B. વક્રતાકેન્દ્ર પર
C. મુખ્ય કેન્દ્ર પર
D. મુખ્ય કેન્દ્ર અને વક્રતાકેન્દ્રની વચ્ચે
ઉત્તર:
વક્રતાકેન્દ્ર પર

પ્રશ્ન 32.
અંતર્ગોળ અરીસાની મદદથી વસ્તુનું વાસ્તવિક અને નાનું પ્રતિબિંબ મેળવવા વસ્તુને ક્યાં મૂકવી જોઈએ?
A. મુખ્ય કેન્દ્ર અને ધૃવની વચ્ચે
B. વક્રતાકેન્દ્ર પર
C. મુખ્ય કેન્દ્ર અને વક્રતાકેન્દ્રની વચ્ચે
D. વક્રતાકેન્દ્રથી દૂર
ઉત્તર:
વક્રતાકેન્દ્રથી દૂર

પ્રશ્ન 33.
અંતર્ગોળ અરીસાની મદદથી વસ્તુનું વાસ્તવિક અને મોટું પ્રતિબિંબ મેળવવા વસ્તુને ક્યાં મૂકવી જોઈએ?
A. ધ્રુવ અને મુખ્ય કેન્દ્રની વચ્ચે
B. મુખ્ય કેન્દ્ર પર
C. મુખ્ય કેન્દ્ર અને વક્રતાકેન્દ્રની વચ્ચે
D. વક્રતાકેન્દ્ર પર
ઉત્તર:
મુખ્ય કેન્દ્ર અને વક્રતાકેન્દ્રની વચ્ચે

પ્રશ્ન 34.
અંતર્ગોળ અરીસા વડે કેવું પ્રતિબિંબ મેળવી શકાતું નથી?
A. વાસ્તવિક અને મોટું
B. વાસ્તવિક અને નાનું
C. આભાસી અને મોટું
D. આભાસી અને નાનું
ઉત્તર:
આભાસી અને નાનું

પ્રશ્ન 35.
બહિર્ગોળ અરીસા વડે હંમેશાં કેવા પ્રકારનું પ્રતિબિંબ મળે છે?
A. વાસ્તવિક, ઊલટું અને નાનું
B. આભાસી, ચતું અને નાનું
C. વાસ્તવિક, ઊલટું અને મોટું
D. આભાસી, ચતું અને મોટું
ઉત્તર:
આભાસી, ચતું અને નાનું

પ્રશ્ન 36.
પ્રકાશનું ત્રાંસું કિરણ કાચમાંથી હવામાં પ્રવેશતાં શું થાય છે?
A. તે લંબ તરફ વળે છે.
B. તે લંબથી દૂર જાય છે.
C. તે વક્રીભવન પામતું નથી.
D. તે મૂળ દિશામાં પરાવર્તન પામે છે.
ઉત્તર:
તે લંબથી દૂર જાય છે.

પ્રશ્ન 37.
એક બિંદુવત્ વસ્તુમાંથી બધી દિશાઓમાં કિરણો છૂટે છે. તે વસ્તુમાંથી છૂટેલું કિરણ, કે જે એક અંતર્ગોળ અરીસાના મુખ્ય અક્ષને સમાંતર છે, તે ધ્યાનમાં લો. પરાવર્તિત કિરણને દોરવા માટેના જરૂરી બિંદુઓમાંનું એક બિંદુ આકૃતિમાં દર્શાવ્યા મુજબનું આપાતબિંદુ પોતે જ છે.

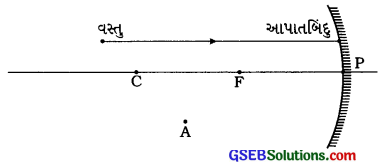
અહીં આપેલી આકૃતિમાંનું એક એવું બિંદુ પસંદ કરો, જેમાંથી પરાવર્તિતકિરણ પસાર થાય છે.
A. C
B. F
C. A
D. P
ઉત્તર:
F

પ્રશ્ન 38.
બહિર્ગોળ લેન્સ વડે કેવું પ્રતિબિંબ મેળવી શકાતું નથી?
A. વાસ્તવિક અને નાનું
B. વાસ્તવિક અને મોટું
C. આભાસી અને નાનું
D. આભાસી અને મોટું
ઉત્તર:
આભાસી અને નાનું

પ્રશ્ન 39.
નીચેનામાંથી કયા અક્ષર(આલ્ફાબેટ)ના પ્રતિબિંબની બાજુઓ અરીસામાં ઊલટાયેલી જોઈ શકાતી નથી?
A. N
B. O
C. P
D. Q
ઉત્તર:
O

પ્રશ્ન 40.
નીચેનામાંથી ક્યા અક્ષર(આલ્ફાબેટ)ના પ્રતિબિંબની બાજુઓ અરીસામાં ઊલટાયેલી જોઈ શકાય છે?
A. W
B. X
C. Y
D. Z
ઉત્તર:
Z

પ્રશ્ન 41.
એક બાળક સમતલ અરીસા સામે ઝડપ vથી દોડી રહ્યું છે, તો તેનું અરીસામાં દેખાતું પ્રતિબિંબ તેની સામે કેટલી ઝડપથી દોડતું દેખાશે?
A. 2v
B. v
C. > v
D. < v
ઉત્તર:
2v

પ્રશ્ન 42.
જો એક ગોલીય અરીસાને પાણીમાં ડુબાડવામાં આવે, તો તેની કેન્દ્રલંબાઈ …….
A. બદલાય છે.
B. બદલાતી નથી.
C. બદલાય કે ન પણ બદલાય.
D. શૂન્ય બને છે.
ઉત્તર:
બદલાતી નથી.

પ્રશ્ન 43.
10 cm કેન્દ્રલંબાઈવાળા બહિર્ગોળ લેન્સની સામે મુખ્ય અક્ષ પર વસ્તુને લંબરૂપે મૂકેલી છે. જો વસ્તુ લેન્સથી 15 cm અંતરે હોય, તો તેનું પ્રતિબિંબ ક્યાં પડશે?
A. F₂ પર
B. F₂ અને 2F₂ ની વચ્ચે
C. 2F₂ પર
D. 2F₂થી દૂર
ઉત્તર:
22થી દૂર

પ્રશ્ન 44.
કયા અરીસા કે લેન્સ માટે તેની સામે મુખ્ય અક્ષ પરના નિશ્ચિત સ્થાને વસ્તુ મૂકી હોય, તો પ્રતિબિંબ પણ તે જ સ્થાને મેળવી શકાય છે?
A. બહિર્ગોળ અરીસો
B. બહિર્ગોળ લેન્સ
C. અંતર્ગોળ લેન્સ
D. અંતર્ગોળ અરીસો
ઉત્તર:
અંતર્ગોળ અરીસો

પ્રશ્ન 6.
નીચેના પ્રશ્નોના માગ્યા પ્રમાણે ઉત્તર આપો (પ્રકીર્ણ) :

પ્રશ્ન 1.
સ્નેલનો નિયમ ગાણિતિક સ્વરૂપમાં લખો.
ઉત્તર:
સ્નેલનો નિયમઃ જો આપાતકોણ 1 અને વક્રીભૂતકોણ r હોય, તો
\(\frac{\sin i}{\sin r}\) = અચળ.
આ અચળ મૂલ્યને પ્રથમ માધ્યમની સાપેક્ષે બીજા માધ્યમનો વક્રીભવનાંક કહે છે.

પ્રશ્ન 2.
પાંચ પારદર્શક માધ્યમો છે, જે એકબીજા સાથે ભૌતિક રીતે સંલગ્ન છે. તો પ્રથમ માધ્યમની સાપેક્ષે પાંચમા માધ્યમનો વક્રીભવનાંક શોધવાનું સૂત્ર લખો.
ઉત્તર:
n₅₁ = \(\frac{n_{5}}{n_{1}}\)

પ્રશ્ન 3.
જો ગોલીય અરીસાની વક્રતાત્રિજ્યા 40 cm હોય, તો તેની કેન્દ્રલંબાઈ મીટરમાં કેટલી થાય?
ઉત્તર:
કેન્દ્રલંબાઈ f = \(\frac{\mathrm{R}}{2}\) = \(\frac{40 \mathrm{~cm}}{2}\) = 20 cm = 0.2 m

પ્રશ્ન 4.
અંતગોંળ અરીસાથી 10 cm દૂર મૂકેલી વસ્તુનું વાસ્તવિક પ્રતિબિંબ મળે છે. જો પ્રતિબિંબ વસ્તુ કરતાં ચાર ગણું મોટું હોય, તો અંતગોળ અરીસાની કેન્દ્રલંબાઈ શોધો.
ઉત્તર:
અહીં, u = – 10 cm,
મોટવણી m =-4 (વાસ્તવિક પ્રતિબિંબ)

પ્રશ્ન 5.
બહિર્ગોળ લેન્સ વડે રચાતા પ્રતિબિંબની મોટવણી – 1 ડે છે, તો વસ્તુ-અંતર કેન્દ્રલંબાઈના પદમાં શોધો.
ઉત્તરઃ
અહીં, m = -1 છે.
મોટવણી m = \(\frac{v}{u}\)
∴ -1 = \(\frac{v}{(-u)}\)
∴ v = +u
અરીસા સૂત્ર મુજબ,
\(\frac{1}{f}\) = \(\frac{1}{v}\) – \(\frac{1}{u}\)
\(\frac{1}{f}\) = \(\frac{1}{(+u)}\) – \(\frac{1}{(-u)}\) (∵ v = +u)
∴ \(\frac{1}{f}\) = \(\frac{2}{u}\)
∴ u = 2f

પ્રશ્ન 6.
60 cm કેન્દ્રલંબાઈવાળા અંતર્ગોળ લેન્સથી 40 cm અંતરે એક વસ્તુ મૂકવામાં આવે, તો તેનું પ્રતિબિંબ-અંતર શોધો.
ઉત્તર:
અહીં, f = – 60 cm અને u = -40 cm; v =?

પ્રશ્ન 7.
વિસરિત (અથવા વિકૃત) પરાવર્તન (Diffused reflection) એટલે શું?
ઉત્તર:
જ્યારે પ્રકાશના સમાંતર કિરણો ખરબચડી સપાટી પર પડે છે ત્યારે જુદી જુદી દિશાઓમાં પરાવર્તન પામે છે. આ પ્રકારના પરાવર્તનને વિસરિત (વિકૃત) પરાવર્તન કહે છે. જે પ્રસારિત પરાવર્તન તરીકે પણ ઓળખાય છે.

પ્રશ્ન 8.
બહિર્ગોળ લેન્સ વડે મળતા પ્રતિબિંબની મોટવણીનું મૂલ્ય : ….. હોય છે.
A. > 1
B. < 1
C. = 1
D. ચોક્કસ કહી શકાય નહિ તેવું
ઉત્તર:
A, B અને C

પ્રશ્ન 9.
પાણી ભરેલા કાચના (પારદર્શક) પ્યાલામાં એક પેન્સિલને અડધી પાણીમાં રહે તેમ ત્રાંસી ડુબાડતાં હવા-પાણીના આંતરપૃષ્ઠ આગળ વાંકી વળેલી દેખાય છે. પાણીને બદલે કેરોસીન કે ટર્પેન્ટાઇન જેવું કોઈ પ્રવાહી ઉપયોગ કરીએ તો આટલા જ પ્રમાણમાં વાંકી વળેલી દેખાશે? તમારા ઉત્તર માટેનું કારણ જણાવો.
ઉત્તર:
વક્રીભવન પામતા કિરણનો વક્રીભૂતકોણ માધ્યમના વક્રીભવનાંક પર આધાર રાખે છે. તેથી જુદાં જુદાં પ્રવાહીઓમાં કિરણોની વાંકી વળવાની ક્ષમતા જુદી જુદી હોય છે. ઓછા વક્રીભવનાંક ધરાવતા પ્રવાહીમાં ઓછી અને વધુ વક્રીભવનાંક ધરાવતા પ્રવાહીમાં વધુ ક્ષમતા હોય છે. કેરોસીન અને ટર્પેન્ટાઇનનો વક્રીભવનાંક પાણી કરતાં વધુ હોવાથી તે બે પ્રવાહીઓમાં વાંકા વળવાની ક્ષમતા પાણી કરતાં વધારે હોય.

પ્રશ્ન 10.
પ્રકાશનું કિરણ ત્રાંસું આપાત થઈ હવામાંથી પાણીમાં પ્રવેશે છે. તેનો ગતિપથ દર્શાવતી કિરણાકૃતિ દોરો.
ઉત્તર :

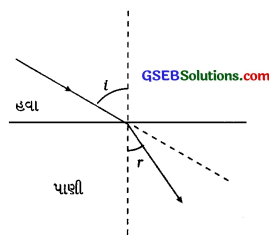
પ્રશ્ન 11.
પ્રકાશનું કિરણ ત્રાંસું આપાત થઈ પાણીમાંથી હવામાં પ્રવેશે છે. તેનો ગતિપથ દર્શાવતી કિરણાકૃતિ દોરો.
ઉત્તર:

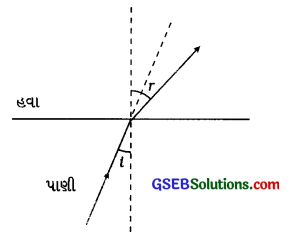
પ્રશ્ન 12.
એક વિદ્યાર્થી કાચના લંબઘન સ્લેબમાંથી પસાર થતાં કિરણનો માર્ગ દોરે છે અને આપાતકોણ , વક્રીભૂતકોણ 7 અને નિર્ગમનકોણ નો નિર્દેશ આકૃતિમાં દર્શાવ્યા મુજબ કરે છે. આકૃતિ જોઈ જણાવો કે કયા ખૂણાને સાચી રીતે દર્શાવેલ છે?

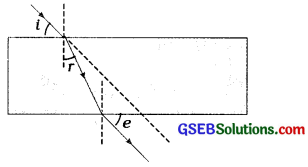
ઉત્તર:
વક્રીભૂતકોણ મુને સાચી રીતે દર્શાવેલ છે.

પ્રશ્ન 13.
સમતલ અરીસાની સપાટી પર લંબરૂપે આપાત થતા પ્રકાશના કિરણનો પરાવર્તનકોણ કેટલો હોય?
ઉત્તર:
પરાવર્તનકોણ r = 0° હોય.

પ્રશ્ન 14.
પ્રકાશનું કિરણ સમતલ અરીસાને તેની સપાટી સાથે 50ગ્ના ખૂણે આપાત થાય છે. તો તેનો પરાવર્તનકોણ કેટલો હશે?
ઉત્તર:
પરાવર્તનકોણ r = 40° હોય.
Hint: સપાટી સાથે આપાતકિરણનો ખૂણો 50° નો છે.
∴ લંબ સાથે આપાતકિરણનો ખૂણો એટલે કે આપાતકોણ i = 90° – 50° = 40°
∴ પરાવર્તનકોણ r = 40°

પ્રશ્ન 15.
જેને આભાસી મુખ્ય કેન્દ્ર હોય તેવા ગોલીય અરીસાનું નામ આપો.
ઉત્તર:
બહિર્ગોળ અરીસો

પ્રશ્ન 16.
અંતર્ગોળ અરીસાના વક્રતાકેન્દ્રમાંથી પસાર થતા હોય તેવા પ્રકાશના કિરણ માટે આપાતકોણ કેટલો હોય?
ઉત્તર:
આપાતકોણ i = 0°
Hint: અંતર્ગોળ અરીસાના વક્રતાકેન્દ્રમાંથી પસાર થતી રેખા અરીસાને લંબ હોય છે.

પ્રશ્ન 17.
નવી કાર્તેઝિયન સંજ્ઞા પ્રણાલી પ્રમાણે નીચેનાની સંજ્ઞા કઈ [+ (ધન) કે – (ત્રણ) છે તે જણાવો :
(a) વાસ્તવિક પ્રતિબિંબની ઊંચાઈ
(b) આભાસી પ્રતિબિંબની ઊંચાઈ
ઉત્તર:
(a) – (ઋણ) (b) + (ધન)

પ્રશ્ન 18.
અંતર્ગોળ અરીસા દ્વારા રચાતા પ્રતિબિંબની મોટવણી
(a) + 3 અને
(b) (-2) હોય, તો પ્રતિબિંબનો પ્રકાર
ઉત્તર:
(a) આભાસી અને ચતું
(b) વાસ્તવિક અને ઊલટું

પ્રશ્ન 19.
30 cm વક્રતાત્રિજ્યાવાળા બહિર્ગોળ અરીસાની સામે ? વસ્તુને ખૂબ જ દૂરના અંતરે મૂકેલ છે. તો તેના પ્રતિબિંબનું સ્થાન જણાવો.
ઉત્તર:
બહિર્ગોળ અરીસાની પાછળ મુખ્ય કેન્દ્ર પર 15 cm અંતરે

પ્રશ્ન 20.
હવાની સાપેક્ષે કાચનો વક્રીભવનાંક \(\frac{3}{2}\) છે. કાચના સાપેક્ષે હવાનો વક્રીભવનાંક લે \(\frac{4}{6}\) છે. તમે આ વિધાન સાથે સંમત છો?
ઉત્તર:
હા

પ્રશ્ન 21.
લેન્સમાંનું બિંદુ જેમાંથી પ્રકાશનું કિરણ પસાર થતાં વિચલિત થતું નથી (વક્રીભવન પામતું નથી) તે બિંદુનું નામ આપો.
ઉત્તર:
પ્રકાશીય કેન્દ્ર

પ્રશ્ન 22.
2 cm ઊંચાઈની વસ્તુને બહિર્ગોળ લેન્સના 2 અંતરે ૬ મૂકેલ છે. તો તેના વડે રચાયેલ પ્રતિબિંબની ઊંચાઈ કેટલી હશે?
ઉત્તર:
પ્રતિબિંબની ઊંચાઈ 2 cm હશે.
રીત: બહિર્ગોળ લેન્સના 2 અંતરે વસ્તુ છે.
∴ પ્રતિબિંબ વાસ્તવિક છે.
u ત્રણ અને તથા f ધન છે.
∴ u = -2f અને v = 2f

પ્રશ્ન 23.
બહિર્ગોળ લેન્સનો ‘વિપુલદર્શક કાચ’ (સૂક્ષ્મદર્શક યંત્ર) તરીકે ઉપયોગ કરવા વસ્તુને ક્યાં મૂકવી જોઈએ?
ઉત્તર:
બહિર્ગોળ લેન્સના પ્રકાશીય કેન્દ્ર અને મુખ્ય કેન્દ્રની વચ્ચે (એટલે કે બહિર્ગોળ લેન્સની કેન્દ્રલંબાઈ કરતાં ઓછા અંતરે)

પ્રશ્ન 24.
આપેલ આકૃતિ તમારી ઉત્તરવહીમાં દોરો અને લેન્સ વડે થતા વક્રીભવનનો માર્ગ દોરી પૂર્ણ કરો.

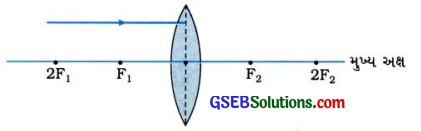
ઉત્તર:

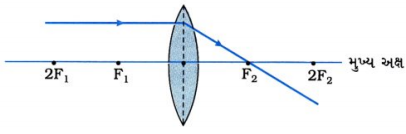
પ્રશ્ન 25.
નીચે આપેલ આકૃતિની નકલ કરો. અંતર્ગોળ લેન્સમાંથી પસાર થતા પ્રકાશના કિરણનું શું થશે તે દર્શાવતી આકૃતિ દોરી તેને પૂર્ણ કરો.

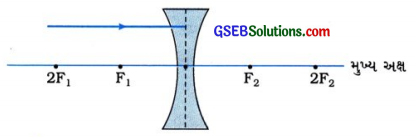
ઉત્તર :

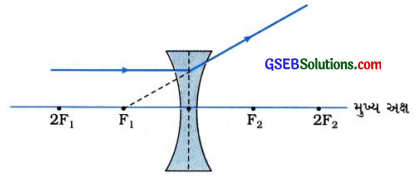
પ્રશ્ન 26.
અંતર્ગોળ લેન્સની સામે 30 cm દૂર મૂકેલી વસ્તુનું લેન્સથી 20 cm દૂર પ્રતિબિંબ રચાય છે. લેન્સની કેન્દ્રલંબાઈ શોધો.
ઉત્તર:
અંતર્ગોળ લેન્સ વડે વસ્તુનું આભાસી અને વસ્તુ તરફ પ્રતિબિંબ રચાય છે.
∴ u ત્રણ અને છ ણ છે.
∴ u = -30 cm અને v = -20 cm
લેન્સ સૂત્ર મુજબ,
\(\frac{1}{f}\) = \(\frac{1}{v}\) – \(\frac{1}{u}\)

પ્રશ્ન 27.
કોનામાંથી પસાર થતાં પ્રકાશનાં કિરણો વધુ વાંકા વળે છે એટલે કે વધારે વક્રીભવન પમાડે છે? મોટી કેન્દ્રલંબાઈવાળો બહિર્ગોળ લેન્સ કે ટૂંકી કેન્દ્રલંબાઈવાળો બહિર્ગોળ લેન્સ?
ઉત્તર:
ટૂંકી કેન્દ્રલંબાઈવાળો બહિર્ગોળ લેન્સ

પ્રશ્ન 28.
કોનો પાવર વધારે છે? એકસમાન દ્રવ્ય(કાચ)નો બનેલો જાડો બહિર્ગોળ લેન્સ કે પાતળો બહિર્ગોળ લેન્સ? તમારી પસંદગીનું કારણ આપો.
ઉત્તર:
જાડો બહિર્ગોળ લેન્સ
કારણઃ જાડા બહિર્ગોળ લેન્સને ટૂંકી કેન્દ્રલંબાઈ હોય છે, તેથી તેનો પાવર વધુ હોય છે.

પ્રશ્ન 29.
અભિસારી લેન્સનો પાવર ધન અને અપસારી લેન્સનો પાવર ઋણ હોય છે. સંમત છો કે અસંમત?
ઉત્તર:
સંમત

પ્રશ્ન 30.
ચશ્માં માટે ડૉક્ટર ચશ્માંની જોડ માટેનું પ્રિસ્ક્રિપ્શન નીચે છે પ્રમાણે છે :
જમણી આંખ -3.5 D, ડાબી આંખ -4.00 D
(a) આ લેન્સની જોડ મધ્યમાં પાતળી છે કે કિનારીએથી પાતળી?
(b) કઈ આંખ વધારે નબળી છે?
ઉત્તર:
(a) મધ્ય ભાગમાં પાતળી
(b) ડાબી આંખ

પ્રશ્ન 31.
એક વ્યક્તિએ આંખના ડૉક્ટર પાસે આંખની તપાસ ? કરાવી. ચશ્માંના લેન્સ માટે પ્રિસ્ક્રિપ્શન નીચે પ્રમાણે છેઃ
જમણી આંખઃ + 2.00 D, ડાબી આંખઃ + 2.50 D
(a) આ લેન્સની જોડ મધ્ય ભાગે જાડી છે કે કિનારીએથી જાડી છે તે જણાવો.
(b) આ ચશ્માંના લેન્સ પ્રકાશનાં કિરણોને કેન્દ્રિત કરે છે કે હું વિકેન્દ્રિત કરે છે તે જણાવો.
ઉત્તર:
(a) મધ્ય ભાગે જાડી
(b) પ્રકાશનાં કિરણોને કેન્દ્રિત કરશે.

પ્રશ્ન 32.
જોડકાં જોડોઃ

ઉત્તર:
(1 – q),
(2 – p).

પ્રશ્ન 33.
જોડકાં જોડો :

ઉત્તર:
(1 – q),
(2 – p).

પ્રશ્ન 34.
કાચના લંબઘન સ્લેબ(ચોસલા)માંથી નિર્ગમન પામતા કિરણનું પાર્શ્વીય સ્થાનાંતર કઈ બે બાબતો પર આધાર રાખે છે તે જણાવો.
ઉત્તર:

1. આપાતકોણ
2. કાચના સ્લેબની જાડાઈ

પ્રશ્ન 35.
અંતર્ગોળ અરીસાના કિસ્સામાં વસ્તુ અને તેના વાસ્તવિક પ્રતિબિંબ વચ્ચેનું ઓછામાં ઓછું (લઘુતમ) અંતર કેટલું હોઈ શકે?
ઉત્તર:
શૂન્ય. (જ્યારે વસ્તુ વક્રતાકેન્દ્ર પર હોય ત્યારે)

પ્રશ્ન 36.
જ્યારે પ્રકાશનું કિરણ વાતાવરણમાં ઉપરની દિશામાં જાય છે, ત્યારે તેનો માર્ગ સામાન્ય રીતે કેવી રીતે બદલાય છે?
ઉત્તર:
પ્રકાશનું કિરણ લંબથી દૂર વાંકું વળે છે.

પ્રશ્ન 37.
અંતર્ગોળ અરીસાના વક્રતાકેન્દ્રમાંથી પસાર થતું પ્રકાશનું કિરણ તે જ માર્ગે શા માટે પરાવર્તન પામે છે? ટૂંકમાં સમજાવો.
ઉત્તર:
અંતર્ગોળ અરીસાના વક્રતાકેન્દ્રમાંથી પસાર થતું પ્રકાશનું ૨ કિરણ અરીસાને લંબરૂપે આપાત થાય છે. તેથી, i = r = 0. તેથી તે જ માર્ગે પરાવર્તન પામે છે.

પ્રશ્ન 38.
નીચેની આકૃતિમાં અંતર્ગોળ અરીસા પર આપાત થતું ૨ પ્રકાશનું એક કિરણ દર્શાવેલ છે. ફરીથી આકૃતિ દોરો અને અરીસા ? પરથી પરાવર્તન પામેલ કિરણનો માર્ગ પૂર્ણ કરો.

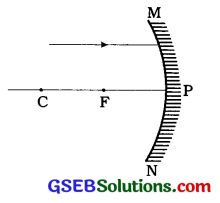
ઉત્તર:

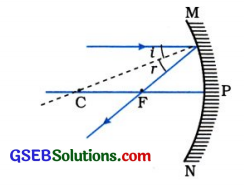
પ્રશ્ન 39.
નીચેની આકૃતિમાં બહિર્ગોળ અરીસા પર આપાત થતું પ્રકાશનું કિરણ દર્શાવેલ છે. ફરીથી આકૃતિ દોરો અને અરીસા પરથી પરાવર્તન પામેલ કિરણનો માર્ગ પૂર્ણ કરો.

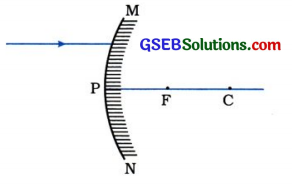
ઉત્તર:

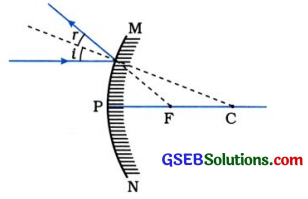
પ્રશ્ન 40.
વક્રીભવનાંકનો એકમ શો છે?
ઉત્તર:
વક્રીભવનાંકને એકમ નથી. તે બે સમાન રાશિઓનો ગુણોત્તર હોવાથી એકમરહિત છે.

પ્રશ્ન 41.
એક માધ્યમમાંથી બીજા માધ્યમમાં પ્રવેશતા પ્રકાશના કિરણ માટે વાંકા વળવાની ઘટના ન થવાની (એટલે કે વિચલિત ન થવાની) શરતો જણાવો.
ઉત્તર:

1. પ્રકાશનું કિરણ બે માધ્યમોને જોડતી સપાટીને લંબરૂપે આપાત થતું હોય.
2. બે જુદાં જુદાં માધ્યમોનો વક્રીભવનાંક સમાન હોય.

પ્રશ્ન 42.
જુદી જુદી ઊંચાઈએ વાતાવરણનો વક્રીભવનાંક જુદો જુદો શા માટે હોય છે?
ઉત્તર:
કારણ કે હવાની ઘનતા ઊંચાઈ બદલાતા બદલાય છે.

પ્રશ્ન 43.
એકસરખા આપાતકોણે માધ્યમ P, Q અને Rમાં પ્રવેશતાં પ્રકાશનાં કિરણોના વક્રીભૂતકોણ અનુક્રમે 450, 35 અને 30° છે. કયા માધ્યમમાં પ્રકાશની ઝડપ સૌથી ઓછી હશે? તમારા ઉત્તર માટે કારણ આપો.
ઉત્તર:
માધ્યમ માં પ્રકાશની ઝડપ સૌથી ઓછી હશે. કારણ: માધ્યમ R માટે વક્રીભૂતકોણ / સૌથી ઓછો છે.
હવે, n = \(\frac{c}{v}\) = \(\frac{\sin i}{\sin r}\) હોવાથી, માધ્યમ Rમાં પ્રકાશની ઝડપ સૌથી ઓછી હોય.

પ્રશ્ન 44.
નીચેની અપૂર્ણ કિરણાતિમાં બહિર્ગોળ લેન્સ વડે વક્રીભવન દ્વારા રચાયેલા પ્રતિબિંબ A’B’ જુઓ.

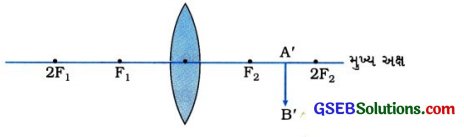
ઉપરની માહિતીના આધારે નીચેની ખાલી જગ્યાઓ પૂરો:

1. વસ્તુ AB(જેને આકૃતિમાં દર્શાવેલ નથી)નું સ્થાન …… હશે.
2. પ્રતિબિંબની સાઇઝ કરતાં વસ્તુની સાઇઝ ………

ઉત્તર:

1. 2F₁થી દૂર
2. મોટી

પ્રશ્ન 45.
રાજુ બહિગોળ લેન્સના ઉપયોગથી મીણબત્તીની જ્યોતનું પ્રતિબિંબ સફેદ પડદા પર ઝીલે છે. તે મીણબત્તીના સ્થાનને 26 cm, લેન્સના સ્થાનને 50 cm અને પડદાના સ્થાનને 74 cm તરીકે નોંધે છે. તો બહિર્ગોળ લેન્સની કેન્દ્રલંબાઈ શોધો.
ઉત્તર:
બહિર્ગોળ લેન્સ માટે f ધન, u ત્રણ અને પ્રતિબિંબ પડદા પર મળતું હોવાથી વાસ્તવિક અને વસ્તુની વિરુદ્ધ બાજુ મળે.
∴ v ધન છે.
અહીં, u = – (મીણબત્તીથી લેન્સનું અંતર) = (-50 – 26)
= -24 cm
v = + (લેન્સથી પડદાનું અંતર) = + |74 – 50 |
= + 24 cm
લેન્સના સૂત્ર \(\frac{1}{f}\) = \(\frac{1}{v}\) – \(\frac{1}{u}\)માં
u = -24 cm અને v = 24 cm મૂકતાં,

બહિર્ગોળ લેન્સની કેન્દ્રલંબાઈ = +12 cm

પ્રશ્ન 46.
આપેલ કિરણાકૃતિનો અભ્યાસ કરો અને સાધન Yનું નામ જણાવો.

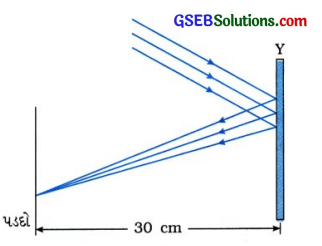
ઉત્તર:
સાધન Y અંતર્ગોળ અરીસો છે.
કારણ સાધન એ સમાંતર કિરણોનું પરાવર્તન કરી એક બિંદુએ પડદા પર કેન્દ્રિત કરે છે.

પ્રશ્ન 47.
દાઢી કરવા માટે અંતર્ગોળ અરીસાનો વપરાશ કરવામાં તેના કયા ગુણધર્મનો ઉપયોગ થાય છે?
ઉત્તર:
અંતર્ગોળ અરીસાના ધ્રુવ અને મુખ્ય કેન્દ્ર વચ્ચે વસ્તુને મૂકતાં તેનું આભાસી, ચતું અને મોટું પ્રતિબિંબ અરીસામાં રચાય છે. અંતગોંળ અરીસાના આ ગુણધર્મનો તેમાં ઉપયોગ થયો છે.

પ્રશ્ન 48.
ગોલીય અરીસા પરના આપેલા બિંદુએથી અરીસાને લંબ કેવી રીતે દોરશો?
ઉત્તર:
ગોલીય અરીસા પરના આપેલા બિંદુને અરીસાના વક્રતાકેન્દ્ર સાથે જોડો અને જરૂર પડ્યે લંબાવો. આ રેખા અરીસાને લંબ છે.

પ્રશ્ન 49.
અંતર્ગોળ અરીસા વડે મળતા પ્રતિબિંબની મોટવણી -1 છે, તો વસ્તુનું સ્થાન જણાવો.
ઉત્તર:
વસ્તુ અંતર્ગોળ અરીસાના વક્રતાકેન્દ્ર પર હશે. m = -1 હોવાથી પ્રતિબિંબ વાસ્તવિક, ઊલટું તથા વસ્તુ જેટલા કદનું છે. તેથી વસ્તુ વક્રતાકેન્દ્ર પર હોય.

પ્રશ્ન 50.
એક ગોલીય અરીસા વડે રચાતા પ્રતિબિંબની મોટવણી ±2 મેળવી શકાય છે. તે કયા પ્રકારનો અરીસો હોઈ શકે?
ઉત્તર:
તે અંતર્ગોળ અરીસો હશે.
કારણઃ અંતર્ગોળ અરીસા વડે જ વાસ્તવિક અને મોટું તેમજ આભાસી અને મોટું પ્રતિબિંબ મેળવી શકાય છે.

પ્રશ્ન 51.
ભરત અંતર્ગોળ લેન્સ વડે વસ્તુ કરતાં બે ગણું પ્રતિબિંબ મેળવ્યું હોવાનો દાવો કરે છે. તે સાચો છે? તમારા ઉત્તર માટે કારણ આપો.
ઉત્તર:
ભરતનો દાવો સાચો નથી.
કારણ: અંતર્ગોળ લેન્સ વડે હંમેશાં વસ્તુ કરતાં નાનું જ પ્રતિબિંબ મેળવી શકાય છે. તેથી તેનાથી બે ગણું (મોટું) પ્રતિબિંબ મળે નહિ.

પ્રશ્ન 52.
કયું પ્રકાશીય વધારે ઘટ્ટ માધ્યમ છે? વક્રીભવનાંક n = 1.36 ધરાવતું આલ્કોહોલ કે n = 1.63 ધરાવતું કાર્બન ડાયસલ્ફાઈડ?
ઉત્તર:
આલ્કોહોલ કરતાં કાર્બન ડાયસલ્ફાઇડનો વક્રીભવનાંક વધારે છે. તેથી કાર્બન ડાયસલ્ફાઇડ એ આલ્કોહોલ કરતાં વધારે પ્રકાશીય ઘટ્ટ માધ્યમ છે.

પ્રશ્ન 53.
અંતર્ગોળ અરીસા વડે રચાતા પ્રતિબિંબની મોટવણી +3 ડે છે, તો તે પ્રતિબિંબનો પ્રકાર જણાવો.
ઉત્તર:
મોટવણી m = + 3 સૂચવે છે કે પ્રતિબિંબ આભાસી, ચતું અને વસ્તુ કરતાં ત્રણ ગણું મોટું હશે.

પ્રશ્ન 54.
હવાની સાપેક્ષે બરફનો વક્રીભવનાંક 1.31 અને ખનિજ મીઠાનો વક્રીભવનાંક 1.54 છે. બરફની સાપેક્ષે ખનિજ મીઠાના વક્રીભવનાંકની ગણતરી કરો.
ઉકેલ:
અહીં, n_ia = 1.31 અને n_ra = 1.54 છે. n_ri = ?
હવે, n_ri = \(\frac{n_{\mathrm{ra}}}{n_{\mathrm{ia}}}\) = \(\frac{1.54}{1.31}\) = 1.17

પ્રશ્ન 55.
અંતર્ગોળ અરીસા વડે રચાતા પ્રતિબિંબનું સ્થાન નક્કી કરવા કેટલા ઓછામાં ઓછી સંખ્યાનાં કિરણોની જરૂર છે?
ઉત્તર:
અંતર્ગોળ અરીસા વડે રચાતા પ્રતિબિંબનું સ્થાન નક્કી કરવા ઓછામાં ઓછા બે કિરણોની જરૂર છે.

પ્રશ્ન 56.
આપેલ ગોલીય અરીસાનું વસ્તુ-અંતર બદલવાથી તેની કેન્દ્રલંબાઈ બદલાય નહિ, પરંતુ પ્રતિબિંબની રેખીય મોટવણી બદલાઈ શકે છે. સંમત છો કે અસંમત?
ઉત્તર:
સંમત

પ્રશ્ન 57.
નીચેની આકૃતિમાં આપાતકોણ, નિર્ગમનકોણ, વક્રીભૂતકોણ અને પાર્વીય સ્થાનાંતરને દર્શાવતા ક્રમાંકને અનુક્રમમાં ગોઠવી લખો :

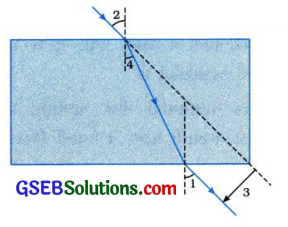
ઉત્તર:
2, 3, 4, 3

પ્રશ્ન 58.
નીચેની ત્રણ આકૃતિઓમાં દરેકમાં બે માધ્યમોની જોડ માટે આપાતકિરણ અને વક્રીભૂતકિરણ દર્શાવ્યા છે. તેમના વક્રીભવનાંક વચ્ચેનો સંબંધ દર્શાવો.

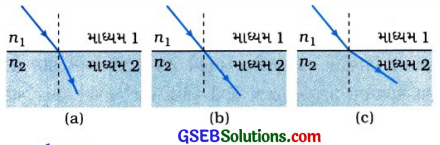
ઉત્તર:
(a) n₁ < n₂

પ્રશ્ન 59.
લેન્સની કેન્દ્રલંબાઈ કઈ કઈ બાબતો પર આધાર રાખે છે?
ઉત્તર:
લેન્સની કેન્દ્રલંબાઈ નીચેની બાબતો પર આધાર રાખે છે :

1. લેન્સની વક્રાકાર સપાટીઓની વક્રતાત્રિજ્યા પર
2. લેન્સના દ્રવ્યની જાત
3. લેન્સ જે માધ્યમમાં મૂકેલ છે તેના પ્રકાર પર

(નોંધઃ આપાતકિરણની આવૃત્તિ પર પણ આધાર રાખે છે. ].

પ્રશ્ન 60.
લેન્સ વડે રચાતાં પ્રતિબિંબોની મોટવણી નીચે આપેલ છે. તે પરથી લેન્સનો પ્રકાર, વસ્તુનું સ્થાન, પ્રતિબિંબનું સ્થાન અને પ્રતિબિંબનો પ્રકાર જણાવો.
(1) m = + 0.6
(2) m = -3
(3) m = \(\frac{1}{2}\)
(4) m = –\(\frac{1}{3}\)
(5) m = -1
ઉત્તર :

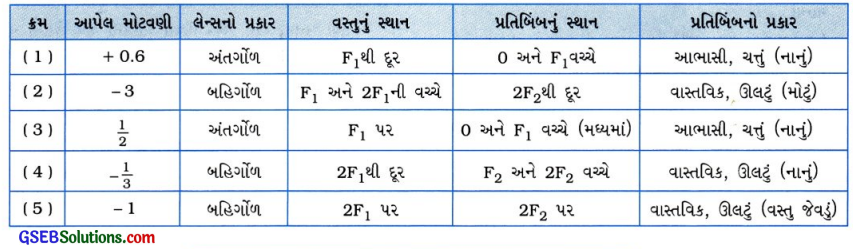
મૂલ્યો આધારિત પ્રશ્નોત્તર (Value Based Questions with Answers)

• નીચે આપેલ દરેક ફકરો વાંચો અને તેની નીચે આપેલા પ્રશ્નોના ઉત્તર આપો:

પ્રશ્ન 1.
બે ખાસ મિત્રો (સખીઓ) અંજલી અને શ્વેતા મોટા ભાગનો સમય સાથે ગુજારતા. એક દિવસ અંજલીએ જોયું અને જાણ્યું કે શ્વેતાને સ્કૂલના લંચ સમયે જમતા દાંતના પેઢામાં દુખે છે. અંજલીના પિતા દાંતના ડૉક્ટર હતા. તેથી તેણીએ શ્વેતાને તેની સાથે તેના પિતાના દવાખાને આવવા સલાહ આપી. અંજલીના પિતાએ શ્વેતાનું મોં અને દાંત અરીસા વડે પ્રકાશમાં તપાસ્યા. તેમણે શ્વેતાને વધુ પડતી ચૉકલેટ નહિ ખાવાની અને ઠંડા પીણાં નહિ પીવાની સલાહ આપી. આ પછી શ્વેતાએ મોંની કાળજી લેવાનું શરૂ કર્યું. તેણે ખાધા પછી મોં સારી રીતે કોગળા કરી સાફ કરવાનું અને કૅલ્શિયમયુક્ત ખોરાક લેવાનું શરૂ કર્યું.

પ્રશ્ન 1.
દાંતના ડૉક્ટર કયા પ્રકારના અરીસાનો ઉપયોગ કરે છે?
ઉત્તર:
અંતર્ગોળ અરીસો

પ્રશ્ન 2.
ડૉક્ટરે શ્વેતાના દાંત તપાસવા પ્રકાશની કઈ ઘટનાનો ઉપયોગ કર્યો?
ઉત્તર:
પ્રકાશના પરાવર્તનની ઘટના

પ્રશ્ન 3.
અંજલીએ કયાં સદ્ગુણો પ્રદર્શિત કર્યા?
ઉત્તર:
સદ્ગુણો:

1. મિત્રતા
2. બીજાની દરકાર
3. મદદરૂપ થવાની ભાવના

પ્રશ્ન 2.
એક નાના શહેરના મેળામાં અમેય તેના મિત્રને લઈને ગયો. ત્યાં તેણે તેના મિત્રને એક અરીસામાં તેનું પ્રતિબિંબ બતાવ્યું. તેમાં તેના શરીરનો ઉપરનો અડધો ભાગ ખૂબ જાડો અને નીચેનો અડધો ભાગ ખૂબ પાતળો જોયો. અમેયનો મિત્ર દ્વિધામાં પડી ગયો. પરંતુ અમેયે તેના મિત્રને અરીસામાં તેના જેવું જ પ્રતિબિંબ બતાવી સાચી સમજ આપી.

પ્રશ્ન 1.
મેળાની દુકાનમાં કયા બે પ્રકારના અરીસા વપરાયા હતા તેમના નામ આપો.
ઉત્તર:
અંતર્ગોળ અને બહિર્ગોળ અરીસો

પ્રશ્ન 2.
જે અરીસામાં પ્રતિબિંબ નાનું મળે છે તે અરીસાનું નામ આપો.
ઉત્તર:
બહિર્ગોળ અરીસો

પ્રશ્ન 3.
અમે ક્યા સદ્ગુણો પ્રદર્શિત કર્યા?
ઉત્તર :
સદ્ગણો:

1. મિત્રભાવ અને
2. સહાનુભૂતિ

પ્રશ્ન 3.
પ્રશાંત તેની ગાડી(કાર)માં ઑફિસે જઈ રહ્યો હતો. ગાડી ચલાવતી વખતે પ્રશાંતે તેના સાઇડ ગ્લાસમાં જોયું કે, તેની પાછળ એક માણસ મોટરસાઈકલ પર આવી રહ્યો છે. મોટરસાઈકલ પર માણસની પાછળ એક સ્ત્રી બેઠી હતી. અચાનક તેના સાઇડ ગ્લાસમાં જોતાં ધ્યાન પર આવ્યું કે, પેલી સ્ત્રીની સાડી મોટરસાઈકલના પૈડાના સ્પોક(સળિયા)ને અડી રહી છે. પ્રશાંત મોટરસાઇકલવાળાને ઊભા રહેવા અને સ્ત્રીને સાવચેત કરવા સંકેત કર્યો. પેલી સ્ત્રીએ પોતાની સાડી વ્યવસ્થિત કરી અને સાવચેત કરવા બદલ પ્રશાંતનો આભાર માન્યો.

પ્રશ્ન 1.
સાઈડ ગ્લાસ તરીકે કયા પ્રકારનો અરીસો વપરાય છે?
ઉત્તર:
બહિર્ગોળ અરીસો

પ્રશ્ન 2.
આ અરીસા વડે રચાતા પ્રતિબિંબની બે લાક્ષણિકતાઓ જણાવો.
ઉત્તર:
બે લાક્ષણિકતાઓ :

1. આભાસી અને ચતું
2. વસ્તુ કરતાં નાનું

પ્રશ્ન 3.
આ બનાવમાં પ્રશાંત વડે પ્રદર્શિત કરવામાં આવેલા સદ્ગુણો જણાવો.
ઉત્તર :
સદ્ગણો

1. જાગૃતતા
2. અન્યની દરકાર
3. જવાબદાર નાગરિકત્વ

પ્રશ્ન 4.
એક કારમાં ચાર મિત્રો અમદાવાદથી વડોદરા જતા હતા. સંજય કાર ચલાવી રહ્યો હતો. તેણે ગાડીના સાઈડ ગ્લાસમાંથી જોયું કે પોતાની ગાડીની પાછળ આવી રહેલી ગાડીને અકસ્માત થયો છે. તેણે અચાનક બ્રેક મારી. તેના મિત્રોએ તેને કઈ બન્યું નથી તેમ માની આ પરિસ્થિતિ છોડી જવા કહ્યું. પરંતુ સંજય તેમની વાતને સંમત થયો નહિ. તે ગાડીમાંથી નીચે ઊતર્યો અને મિત્રોને મનાવી ઈજાગ્રસ્તને મદદ કરવા કહ્યું. બધા ઈજા પામેલ વ્યક્તિને નજીકની હૉસ્પિટલમાં લઈ ગયા. હૉસ્પિટલમાં પ્રાથમિક સારવાર લીધી. અકસ્માતનો ભોગ બનનાર વ્યક્તિએ જીંદગી બચાવવા બદલ બધાનો આભાર માન્યો.

પ્રશ્ન 1.
સંજયે જેનાથી અકસ્માત જોયો તે અરીસાનો પ્રકાર જણાવો.
ઉત્તર:
બહિગોળ અરીસો

પ્રશ્ન 2.
વાહનોમાં “સાઈડ ગ્લાસ’ તરીકે આ પ્રકારનો અરીસો શા માટે વપરાય છે?
ઉત્તર:
બહિર્ગોળ અરીસો બહારની તરફ વક્રાકાર હોવાથી તે વિશાળ દષ્ટિ-ક્ષેત્ર ધરાવે છે. તેથી ડ્રાઇવર પાછળના ઘણા મોટા વિસ્તારનું દશ્ય જોઈ શકે છે.

પ્રશ્ન 3.
સંજયના પાત્ર પરથી તમે શું શીખ મેળવી?
ઉત્તર:
સંજયના મદદરૂપ થવાના સ્વભાવ પરથી આપણે શીખવું જોઈએ કે જરૂરિયાતવાળા લોકોને મદદ કરવી.

પ્રશ્ન 5.
એક વસાહતમાં(કોલોની)માં રોડના બંધ છેડે પુષ્કળ અકસ્માત થવાના બનાવો બનતા હતા. એક દિવસ શાલિની બંધ છેડાની નજીકના મકાનમાં આવ્યા. તેમણે ત્યાં અકસ્માત થતો જોયો.
તેઓ તરત જ અકસ્માતની જગ્યાએ દોડી ગયા અને ભોગ બનનારને પ્રાથમિક સારવાર આપી. પછી તેમણે ફોન કરી ઍબ્યુલન્સ બોલાવી. ત્યારબાદ તેઓ કૉલોનીના વેલ્ફર કમિટિના પ્રમુખને મળ્યા. તેમણે રસ્તાના બંધ છેડે બંને બાજુ મોટા બહિર્ગોળ અરીસા મૂકાવવાની વિનંતી કરી. અરીસા મૂકાવ્યા પછી અકસ્માત થવાના બનાવો એકદમ ઘટી ગયા.

પ્રશ્ન 1.
શાલિનીએ રોડના બંધ છેડે બંને બાજુ મોટા બહિર્ગોળ અરીસા મુકાવવાની સલાહ શા માટે આપી?
ઉત્તર:
બહિર્ગોળ અરીસો વિશાળ દષ્ટિ-ક્ષેત્ર ધરાવે છે તેને કારણે રોડના બંધ છેડે અથવા બંધ છેડાની બંને બાજુનો વાહનવ્યવહાર જોઈ શકાય છે. શાલિની આ હકીકતથી વાકેફ હતી. તેથી
તેણીએ મોટા બહિર્ગોળ અરીસા મુકાવવાની સલાહ આપી.

પ્રશ્ન 2.
તમારા મતે શાલિનીના કયા સદ્ગુણો પ્રદર્શિત થાય છે?
ઉત્તર:
શાલિનીના સદ્ગુણો :

1. બીજાની મુશ્કેલીની દરકાર કરવી
2. જ્ઞાનનો સાચો ઉપયોગ કરવો

પ્રશ્ન 3.
તમારા મતે કૉલોનીના વેલ્ફર કમિટિના પ્રમુખના કયા સદ્ગુણો પ્રદર્શિત થાય છે?
ઉત્તર:
કૉલોનીના પ્રમુખના સદ્ગણોઃ

1. બીજાને સમજવાનો સ્વભાવ
2. ફરજનું ભાન
3. બીજાની સલામતીની દરકાર

પ્રાયોગિક કૌશલ્યો આધારિત પ્રશ્નોત્તર (Practical Skill Based Questions with Answers)

પ્રશ્ન 1.
નીચેની આકૃતિ જોઈ પ્રશ્નોના ઉત્તર લખો:

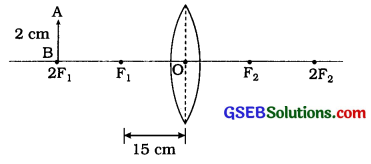
પ્રશ્ન 1.
વસ્તુ-અંતર u અને કેન્દ્રલંબાઈની કિંમત જણાવો.
ઉકેલ:
વસ્તુ 2F₁ (વક્રતાકેન્દ્ર) પર છે.
∴ u = R = – (15 × 2) = – 30 cm;
તથા f = +15 cm (આપેલ છે, કારણ કે લેન્સ બહિગોળ છે.)

પ્રશ્ન 2.
AB વસ્તુના પ્રતિબિંબનું અંતર છે તથા ઊંચાઈ h’ જણાવો.
ઉકેલ:
વસ્તુ 2F₁ પર હોવાથી વાસ્તવિક પ્રતિબિંબ વસ્તુ જેવડું તથા 2F₂ પર મળે.
∴ v = R = +30 cm
વાસ્તવિક પ્રતિબિંબ વસ્તુ જેવડું (h = 2 cm જેવડું) હોય તથા 2F₂ પર મળે છે.
∴ h’ ત્રણ હોય તથા h’ = -h = -2 cm
∴ h’ = -2 cm

પ્રશ્ન 3.
મોટવણી m જણાવો.
ઉકેલ:
પ્રતિબિંબ વાસ્તવિક, ઊલટું અને વસ્તુ જેવડું હોવાથી મોટવણી m = -1

પ્રશ્ન 2.
નીચેની આકૃતિ જોઈ પ્રશ્નોના ઉત્તર લખો :

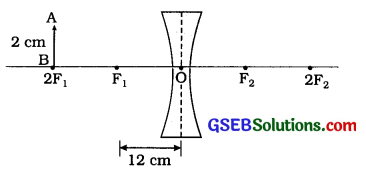
1. વસ્તુ-અંતર u અને કેન્દ્રલંબાઈ ની કિંમત જણાવો.
2. પ્રતિબિંબનો પ્રકાર જણાવો.
3. મોટવણીના માનાંકનું મૂલ્ય 1, 1થી ઓછું કે 1થી વધારે હશે?

ઉકેલ:
અંતર્ગોળ લેન્સ હોવાથી u, v, fનાં મૂલ્યો ઋણ હોય. પ્રતિબિંબ આભાસી, ચતું અને નાનું હોય.

1. u = – (12 × 2) = -24 cm તથા
   f = -12 cm (આપેલ છે, કારણ કે લેન્સ અંતર્ગોળ છે.)
2. પ્રતિબિંબ આભાસી અને ચતું છે.
3. પ્રતિબિંબ આભાસી અને હંમેશાં નાનું છે. |m| < 1

પ્રશ્ન 3.
ત્રણ જુદાં જુદાં અરીસા પરથી પરાવર્તિત થતાં ત્રણ જુદાં જુદાં પરાવર્તિત કિરણો નીચેની આકૃતિઓમાં દર્શાવ્યા છેઃ

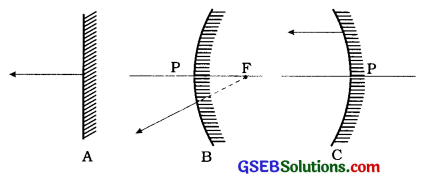
આપેલ આકૃતિનો કાળજીપૂર્વક અભ્યાસ કરી નીચેના પ્રશ્નોના ઉત્તર લખો :

પ્રશ્ન 1.
કયો અરીસો બહિર્ગોળ અરીસો છે?
ઉત્તર:
અરીસો B

પ્રશ્ન 2.
આપેલ અરીસાઓમાંથી કયો અરીસો –

1. સમાંતર કિરણપુંજ રૂપે પ્રકાશનું પરાવર્તન કરશે?
2. આપાત થતાં સમાંતર કિરણોને કેન્દ્રિત કરશે?

ઉત્તર:

1. અરીસો A
2. અરીસો C

પ્રશ્ન 3.
કયો અરીસો હંમેશાં વસ્તુના કદ જેવડું જ પ્રતિબિંબ ઉત્પન્ન કરશે?
ઉત્તર:
અરીસો A

પ્રશ્ન 4.
ક્યો અરીસો વસ્તુના પરિમાણ કરતાં નાનું પ્રતિબિંબ રચશે?
ઉત્તર:
અરીસો B

પ્રશ્ન 5.
ક્યો અરીસો વસ્તુ કરતાં નાનું અથવા મોટું એમ બંને પ્રકારનું પ્રતિબિંબ વસ્તુ-અંતર પર આધારિત રચશે?
ઉત્તર:
અરીસો C

પ્રશ્ન 6.
કયો અરીસો

1. ડ્રેસિંગ ટેબલમાં વપરાય છે?
2. વાહનોમાં “સાઇડ મિરર’ તરીકે વપરાય છે?
3. દાંતના ડૉક્ટર વાપરે છે?

ઉત્તર:

1. અરીસો A
2. અરીસો B
3. અરીસો C

પ્રશ્ન 4.
ગોલીય અરીસા માટે મોટવણીનું સૂત્ર નીચેનાં પદોમાં મેળવો:

પ્રશ્ન 1.
માત્ર ” અને uમાં
ઉત્તર:
અરીસાનું સૂત્ર : \(\frac{1}{v}\) + \(\frac{1}{u}\) = \(\frac{1}{f}\) છે.
∴ \(\frac{-u}{v}\) + \(\frac{-u}{u}\) = \(\frac{-u}{f}\) (બંને બાજુએ –u વડે ગુણતાં)

ઉપરોક્ત મોટવણીનું સૂત્ર અને u પદોમાં છે

પ્રશ્ન 2.
અરીસાનું સૂત્ર \(\frac{1}{v}\) + \(\frac{1}{u}\) = \(\frac{1}{f}\)
\(\frac{-v}{u}\) + \(\frac{-v}{u}\) = \(\frac{-u}{f}\) (બંને બાજુએ – વડે ગુણતાં)
∴ -1 – \(\frac{v}{u}\) = –\(\frac{v}{f}\)
∴ \(\frac{v}{u}\) = 1 – \(\frac{v}{f}\)
∴ \(\frac{-v}{u}\) = \(\frac{f-v}{f}\)
∴ m = \(\frac{f-v}{f}\) (∵ –\(\frac{v}{u}\) = m)
ઉપરોક્ત મોટવણીનું સૂત્ર 5 અને છ પદોમાં છે.

પ્રશ્ન 5.
ગોલીય લેન્સ માટે મોટવણીનું સૂત્ર નીચેનાં પદોમાં મેળવોઃ

1. માત્ર અને પ્રમાં
2. માત્ર અને માં

ઉત્તર:
Hint: ગોલીય લેન્સનું સૂત્ર – \(\frac{1}{v}\) – \(\frac{1}{u}\) = \(\frac{1}{f}\) લઈ ઉપરના
પ્રશ્ન 4 મુજબ ગણતરી કરતાં નીચે મુજબનાં સૂત્રો મળશે.

1. m = \(\frac{f}{f+u}\)
2. m = \(\frac{f-v}{f}\)

પ્રશ્ન 6.
બહિર્ગોળ અરીસાની સામે વસ્તુને લેન્સની કેન્દ્રલંબાઈ જેટલા અંતરે મૂકવામાં આવે તો મળતા પ્રતિબિંબની ઊંચાઈ વસ્તુની ઊંચાઈ કરતાં અડધી હોય છે. આ પરિણામ ફક્ત મોટવણીના સૂત્રના ઉપયોગથી સાબિત કરો.
ઉકેલઃ
બહિર્ગોળ અરીસા માટે u ઋણ, છે અને f ધન હોય છે. અહીં, વસ્તુ-અંતર u = -f છે.
હવે, m = \(\frac{f}{f-u}\) સૂત્ર વાપરો. તેમાં u = -f મૂકતાં,

આમ, પ્રતિબિંબની ઊંચાઈ વસ્તુની ઊંચાઈ કરતાં અડધી છે એમ પુરવાર થાય છે.

પ્રશ્ન 7.
બહિર્ગોળ લેન્સની કેન્દ્રલંબાઈ +10 cm અને અંતર્ગોળ લેન્સની કેન્દ્રલંબાઈ – 10 cm છે. જો બે સરખી ઊંચાઈની વસ્તુઓને બંને લેન્સના મુખ્ય કેન્દ્ર પર મૂકવામાં આવે, તો દરેક લેન્સ વડે રચાતાં પ્રતિબિંબના સ્થાન શોધો.
ઉકેલ:

(1) બહિર્ગોળ લેન્સ માટે : f = + 10 cm અને
u = – 10 cm છે.
વસ્તુને બહિર્ગોળ લેન્સના મુખ્ય કેન્દ્ર F₁ પર મૂકવામાં આવે છે.
∴ તેનું પ્રતિબિંબ અનંત અંતરે મળે. (પ્રાયોગિક જ્ઞાન)
∴ પ્રતિબિંબનું સ્થાન અનંત અંતરે છે.
હવે બીજી રીતે સૂત્રની મદદથી ગણતરી કરીએ.
\(\frac{1}{v}\) – \(\frac{1}{u}\) = \(\frac{1}{f}\) (લેન્સનું સૂત્ર)માં
f = + 10 અને u = – 10 મૂકતાં,
\(\frac{1}{v}\) – \(\frac{1}{u}\) = \(\frac{1}{10}\)
∴ \(\frac{1}{v}\) – \(\frac{1}{-10}\) = \(\frac{1}{10}\)
∴ \(\frac{1}{v}\) + \(\frac{1}{10}\) = \(\frac{1}{10}\)
∴ \(\frac{1}{v}\) = 0 ∴ v = ∞
∴ પ્રતિબિંબનું સ્થાન અનંત અંતરે છે.

(2) અંતર્ગોળ લેન્સ માટે : f = – 10 cm તથા
u = – 10 cm છે.
લેન્સના સૂત્ર \(\frac{1}{v}\) – \(\frac{1}{u}\) = \(\frac{1}{f}\) માં u અને ની કિંમતો મૂકતાં,
\(\frac{1}{v}\) – \(\frac{1}{-10}\) = \(\frac{1}{-10}\)
∴ \(\frac{1}{v}\) = –\(\frac{1}{10}\) – \(\frac{1}{10}\) = –\(\frac{2}{10}\) = –\(\frac{1}{5}\)
∴ v = -5 cm
∴ પ્રતિબિંબનું સ્થાન O છે અને F₁ની વચ્ચે (મધ્યમાં) વસ્તુ તરફની બાજુએ.

પ્રશ્ન 8.
જો p, q, r એ ગોલીય અરીસા માટે અનુક્રમે વસ્તુ-અંતર, પ્રતિબિંબ-અંતર અને વક્રતાત્રિજ્યાનાં મૂલ્યો સૂચવે છે. સાબિત કરો કે, r = \(\frac{2 p q}{p+q}\)
ઉકેલ:
અરીસા સૂત્ર મુજબ \(\frac{1}{f}\) = \(\frac{1}{u}\) + \(\frac{1}{v}\) છે.
વળી, f = \(\frac{r}{2}\)


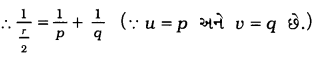
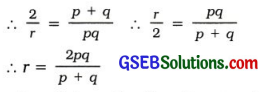
[નોંધઃ ગોલીય અરીસાની પ્રચલિત સંજ્ઞાઓ મુજબ R = \(\frac{2 u v}{u+v}\) થાય.].

પ્રશ્ન 9.
બહિર્ગોળ લેન્સથી 1 મીટર દૂર મૂકેલી વસ્તુનું લેન્સ વડે મળતું પ્રતિબિંબ વાસ્તવિક, ઊલટું અને વસ્તુના પરિમાણ જેટલા પરિમાણનું મળે છે. તો લેન્સની કેન્દ્રલંબાઈ શોધો. તેને દર્શાવતી કિરણાકૃતિ પણ દોરો. ઉકેલ:
બહિર્ગોળ લેન્સ વડે વસ્તુનું પ્રતિબિંબ વાસ્તવિક, ઊલટું અને વસ્તુના પરિમાણ જેટલા પરિમાણમાં મળે છે.
∴ વસ્તુ 2F₁ (વક્રતાકેન્દ્રો ઉપર હોવી જોઈએ તથા તેનું પ્રતિબિંબ વસ્તુની વિરુદ્ધ બાજુએ 2F₂ પર મળે.
આમ, વસ્તુ-અંતર u =- 1 m તથા D = 1 m તથા R = 1 m
∴ f = \(\frac{1}{2}\) m = \(\frac{1}{2}\) (100 cm) = + 50 cm
∴ બહિર્ગોળ લેન્સની કેન્દ્રલંબાઈ = + 50 cm
માગેલ કિરણાકૃતિ નીચે મુજબ છે :

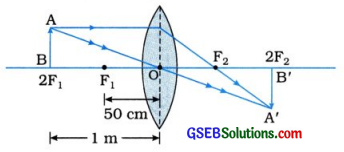
પ્રશ્ન 10.
આકૃતિમાં દર્શાવ્યા મુજબ AB અને CD બે ગોલીય અરીસાઓ છે, જે 7 કેન્દ્રવાળા પોલા ગોળાના 5 ભાગરૂપે છે. ચાપ AB = \(\frac{1}{2}\) ચાપ CD છે. નીચેના પ્રશ્નોના ઉત્તર લખો :
(1) તે બે ગોલીય અરીસાઓની કેન્દ્રલંબાઈનો ગુણોત્તર કેટલો છે?
(2) બે અરીસાઓ પૈકી કયો અરીસો તેની સામે મૂકેલી વસ્તુનું હંમેશાં આભાસી પ્રતિબિંબ રચશે? શા માટે?
ઉકેલ:
(1) બંને અરીસાઓની વક્રતાત્રિજ્યા સમાન છે.
∴ R₁ = R₂
∴ \(\frac{\mathrm{R}_{1}}{2}\) = \(\frac{\mathrm{R}_{2}}{2}\)
∴ |f₁| = |f₂ |
∴ તેમની કેન્દ્રલંબાઈની સંખ્યાત્મક કિંમત સરખી છે. –
∴ \(\frac{\left|f_{1}\right|}{\left|f_{2}\right|}\) = 1 થાય.
AB બહિર્ગોળ અરીસો છે. ∴ તેની કેન્દ્રલંબાઈ + (ધન) છે.
CD અંતર્ગોળ અરીસો છે. ∴ તેની કેન્દ્રલંબાઈ – (ત્રણ) છે.
∴ \(\frac{f_{1}}{f_{2}}\) = -1 થાય.

(2) બે અરીસાઓ પૈકી AB બહિર્ગોળ અરીસો છે.
∴ તે હંમેશાં વસ્તુનું આભાસી પ્રતિબિંબ રચે.

પ્રશ્ન 11.
પાર્શ્વય સ્થાનાંતર એટલે શું? કાચના લંબઘન પર ત્રાંસું આપાત થતું કિરણ આપાતકિરણને સમાંતર નિર્ગમન પામે છે એમ બતાવો.
ઉત્તર:

• ડ્રૉઇંગ બોર્ડ પર સફેદ કાગળ (ડ્રૉઇંગ પેપર) મૂકી તેના પર કાચનો લંબઘન સ્લેબ મૂકો.
• સ્લેબની લંબચોરસ કિનારી પેન્સિલ વડે આંકી લો.
• સ્લેબની એક બાજુ બે પિન A અને B ઊભી ગોઠવો.
• સ્લેબની બીજી બાજુથી સ્લેબમાં પિન A અને B ના પ્રતિબિંબ જુઓ. અને પિન C અને D એવી રીતે ઊભી ગોઠવો કે જેથી ચારેય પિન A, B, C અને D એક સીધી રેખામાં દેખાય.
• સ્લેબ અને પિનો ઊઠાવી લઈ આકૃતિમાં દર્શાવ્યા મુજબ જરૂરી કિરણ અને રેખાઓ દોરો.
• અહીં કિરણ AB આપાતકિરણ, કિરણ OE વક્રીભૂતકિરણ અને કિરણ CD નિર્ગમનકિરણ છે.
• પ્રથમ વક્રીભવન O બિંદુએ માધ્યમ a(હવા)માંથી માધ્યમ b(કાચ)માં પ્રવેશતાં થાય છે. તેમાં i આપાતકોણ અને r વક્રીભવનકોણ છે.

n_ba = \(\frac{\sin i}{\sin r}\) ….. (1)

• દ્વિતીય વક્રીભવન : બિંદુએ માધ્યમ b(કાચ)માંથી માધ્યમ a(હવા)માં પ્રવેશતાં થાય છે.
  તેમાં / આપાતકોણ અને ૯ વક્રીભવનકોણ છે.

∴ n_ab = \(\frac{\sin r}{\sin e}\) …… (2)
(1) અને (2) પરથી,

∴ આપાતકોણ = નિર્ગમનકોણ
∴ આપાતકિરણ AOd એ નિર્ગમનકિરણ CDને સમાંતર છે. આમ, કિરણ AOd || કિરણ CD, પરંતુ આકૃતિ જોતાં તે બાજુમાં FE જેટલું સ્થાનાંતરિત થયેલું છે. આને પાર્શ્વય સ્થાનાંતર કહે છે.

પ્રશ્ન 12.
નીચેના કિસ્સામાં સાધનને ઓળખો, જેમાં કોઈ ગોલીય અરીસો છે કે લેન્સ વપરાયો છે તથા તે દરેક કિસ્સામાં આભાસી અને ચતું પ્રતિબિંબ મળે છે :

પ્રશ્ન 1.
વસ્તુને, સાધન અને તેના મુખ્ય કેન્દ્રની વચ્ચે મૂકેલી છે. પ્રતિબિંબ મોટું અને સાધનની પાછળ રચાય છે.
ઉત્તર:
અંતર્ગોળ અરીસો

પ્રશ્ન 2.
વસ્તુને, સાધન અને તેના મુખ્ય કેન્દ્રની વચ્ચે મૂકેલી છે. પ્રતિબિંબ મોટું અને વસ્તુ જે બાજુ હોય તે બાજુએ રચાય છે.
ઉત્તર:
બહિર્ગોળ લેન્સ

પ્રશ્ન 3.
વસ્તુને, સાધનથી નિશ્ચિત અંતરે (એટલે કે સાધન અને અનંત અંતરની વચ્ચે) મૂકેલી છે. પ્રતિબિંબ નાનું તથા મુખ્ય કેન્દ્ર અને પ્રકાશીય કેન્દ્ર વચ્ચે વસ્તુની બાજુ તરફ જ રચાય છે.
ઉત્તર:
અંતર્ગોળ લેન્સ

પ્રશ્ન 4.
વસ્તુને, સાધનથી નિશ્ચિત અંતરે (એટલે કે સાધન અને અનંત અંતરની વચ્ચે) મૂકેલી છે. પ્રતિબિંબ નાનું તથા ધ્રુવ અને મુખ્ય કેન્દ્રની વચ્ચે તથા ? સાધનની પાછળ રચાય છે.
ઉત્તર:
બહિર્ગોળ અરીસો

પ્રશ્ન 13.
સુધા તેની વિજ્ઞાનની પ્રયોગશાળાની કાચની બારીનું પ્રતિબિંબ લેન્સથી 15 cm દૂર પડદા પર જુએ છે. તેથી હવે બારીના કાચને બદલે બારીની બહાર દેખાતા મકાનને પડદા પર ઝીલવા લેન્સને ખસેડ્યા સિવાય પ્રયત્ન કરે છે. આ માટે તેણીએ મકાનનું સ્પષ્ટ પ્રતિબિંબ મેળવવા પડદાને કઈ દિશામાં ખસેડશે? આ લેન્સની આશરે કેન્દ્રલંબાઈ કેટલી હશે?
ઉત્તર:
બારીના કાચને બદલે મકાનનું સ્પષ્ટ પ્રતિબિંબ મેળવવા સુધાએ પડદાને લેન્સ તરફ થોડો ખસેડવો પડે. આ લેન્સની આશરે કેન્દ્રલંબાઈ 15 cm છે.

પ્રશ્ન 14.
બે સમતલ અરીસાઓની કેવી સ્થિતિમાં ગોઠવણી કરવાથી આપાતકિરણ અને પરાવર્તિતકિરણ પરસ્પર હંમેશાં સમાંતર મળશે? (આપાતકોણ ગમે તે હોય, તેમ છતાં આ સત્ય છે.) આકૃતિ દોરી આ બાબત દર્શાવો.
ઉત્તર:
જ્યારે બે સમતલ અરીસાઓને એકબીજા સાથે 90ના ખૂણે મૂકવામાં આવે તો આપાતકિરણ અને પરાવર્તિતકિરણ હંમેશાં પરસ્પર સમાંતર હશે. આપાતકોણ ગમે તે રાખવામાં આવે તો પણ આ વિધાન સત્ય છે. આ બાબત નીચેની આકૃતિમાં આપાતકોણ = 45° લઈને દર્શાવી છે.

પ્રશ્ન 15.
નીચે આપેલી આકૃતિનો કાળજીપૂર્વક અભ્યાસ કરી તેની નીચે આપેલા પ્રશ્નોના ઉત્તર આપો:

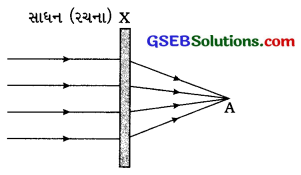
પ્રશ્ન 1.
પ્રકાશકિરણોનો માર્ગ કઈ ઘટનાને લીધે બદલાય છે?
ઉત્તર:
વક્રીભવન

પ્રશ્ન 2.
સાધન (રચના) Xનું નામ જણાવો.
ઉત્તર:
બહિર્ગોળ લેન્સ

પ્રશ્ન 3.
બિંદુ A ને શું કહેવાય?
ઉત્તર:
લેન્સનું મુખ્ય કેન્દ્ર

પ્રશ્ન 4.
સાધન (રચના) X અને A બિંદુ વચ્ચેના અંતરના વ્યસ્તને કઈ રાશિ કહેવામાં આવે છે?
ઉત્તર:
લેન્સનો પાવર

પ્રશ્ન 5.
પ્રશ્ન (4)ના ઉત્તરની ભૌતિક રાશિનો SI એકમ લખો.
ઉત્તર:
D (ડાયોપ્ટર)

પ્રશ્ન 16.
નીચેની પરિસ્થિતિનો કાળજીપૂર્વક અભ્યાસ કરી તેની નીચે આપેલા પ્રશ્નોના ઉત્તર લખોઃ
જ્યારે 6 cm ઊંચાઈની એક વસ્તુ લેન્સના પ્રકાશીય કેન્દ્રથી 12 cm અંતરે મૂકવામાં આવે છે, ત્યારે વસ્તુનું 12 cm ઊંચાઈવાળું ચતું પ્રતિબિંબ રચાય છે, તો

પ્રશ્ન 1.
લેન્સનો પ્રકાર જણાવો.
ઉકેલ:
બહિર્ગોળ લેન્સ

પ્રશ્ન 2.
પ્રતિબિંબની મોટવણી શોધો.
ઉકેલ:
m = 2.
રીત: m = \(\frac{h^{\prime}}{h}\) = \(\frac{12 \mathrm{~cm}}{6 \mathrm{~cm}}\) = 2

પ્રશ્ન 3.
પ્રતિબિંબ-અંતર અને લેન્સની કેન્દ્રલંબાઈ શોધો.
ઉકેલ:
v = -24 cm અને f = 24 cm
રીતઃ m = 1
∴ v = m × u
∴ v = 2 × (-12)
∴ v = – 24 cm

પ્રશ્ન 4.
લેન્સનો પાવર કેટલો હશે?
ઉકેલ:
P = 4.167 D
રીત: P = \(\frac{1}{f}\) = \(\frac{1}{0.24 \mathrm{~m}}\) = \(\frac{100}{24}\) = 4.167 D

પ્રશ્ન 5.
આ લેન્સનો રોજબરોજના જીવનમાં ઉપયોગ લખો.
ઉકેલ:
મૅગ્નિફાઇંગ લેન્સ તરીકે

પ્રશ્ન 17.
નીચેની પરિસ્થિતિનો કાળજીપૂર્વક અભ્યાસ કરી તેની નીચે આપેલા પ્રશ્નોના ઉત્તર લખોઃ
જ્યારે ગોલીય અરીસાના ધ્રુવથી વસ્તુને 12 cm અંતરે મૂકવામાં આવે છે, ત્યારે અરીસાની આગળ 48 cm અંતરે તે વસ્તુનું પ્રતિબિંબ રચાય છે, તો

પ્રશ્ન 1.
અરીસાનો પ્રકાર જણાવો.
ઉકેલ:
અંતર્ગોળ અરીસો
(∵ પ્રતિબિંબ અરીસાની આગળ અને મોટું છે.)

પ્રશ્ન 2.
પ્રતિબિંબની મોટવણી શોધો.
ઉકેલ:
m = -4 (∵ m = –\(\frac{v}{u}\) = – \(\frac{-48}{-12}\) = -4)

પ્રશ્ન 3.
અરીસાની કેન્દ્રલંબાઈ શોધો.
ઉકેલ:
f = – 9.6 cm

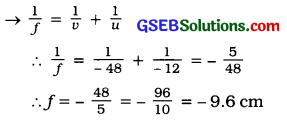
પ્રશ્ન 4.
જો વસ્તુની ઊંચાઈ 5 cm હોય, તો પ્રતિબિંબની ઊંચાઈ શોધો.
ઉકેલ:
h’ = -20 cm

• m = \(\frac{h^{\prime}}{h}\) ∴ -4 = \(\frac{h^{\prime}}{5}\). ∴ h’ = -20 cm

પ્રશ્ન 5.
આ અરીસાનો ઉપયોગ જણાવો.
ઉકેલ:

• વાહનોની હેડલાઇટમાં પરાવર્તક તરીકે,
• દાઢી કરવા તથા મેક-અપ કરવા.