Gujarat Board GSEB Solutions Class 6 Maths Chapter 14 પ્રાયોગિક ભૂમિતિ Ex 14.2 Textbook Exercise Questions and Answers.
Gujarat Board Textbook Solutions Class 6 Maths Chapter 14 પ્રાયોગિક ભૂમિતિ Ex 14.2
પ્રશ્ન 1.
માપપટ્ટીનો ઉપયોગ કરીને 7.3 સેમી લંબાઈનો રેખાખંડ દોરો.
ઉત્તરઃ
- કાગળ ઉપર બિંદુ A નક્કી કરો.
- માપપટ્ટી એવી રીતે ગોઠવો કે માપપટ્ટી ઉપરનું શૂન્ય એ A બિંદુ આગળ રહે.

- પેન્સિલ વડે માપપટ્ટી ઉપર 7.3 સેમી અંતરે બિંદુ B નક્કી કરતું ટપકું કરો.
- A અને B બિંદુઓ જોડો.
આમ, \(\overline{A B}\) એ માગ્યા મુજબનો 7.3 સેમી લંબાઈનો રેખાખંડ છે.
![]()
પ્રશ્ન 2.
માપપટ્ટી અને પરિકરના ઉપયોગથી 5.6 સેમી લંબાઈનો રેખાખંડ રચો.
ઉત્તરઃ
- માપપટ્ટી વડે રેખા l રચો અને તેની ઉપર બિંદુ A લો.
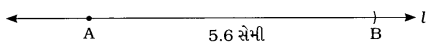
- માપપટ્ટી ઉપરના શૂન્ય ઉપર પરિકરની અણી મૂકી પેન્સિલની અણી 5.6 સેમીએ રહે તેટલું ચાપ લો.
- હવે પરિકરનું માપ ન બદલાય એ રીતે પરિકરની અણી l રેખા પરના A બિંદુ ઉપર મૂકી l રેખા ઉપર ચાપ દોરો.
- ચાપ રેખા lને જ્યાં કાપે ત્યાં બિંદુ B કહો.
આમ, \(\overline{A B}\) એ 5.6 સેમી લંબાઈનો રેખાખંડ છે.
પ્રશ્ન 3.
7.8 સેમી લંબાઈનો \(\overline{A B}\) રચો. આમાંથી 4.7 સેમી લંબાઈનો \(\overline{A C}\) કાપો. \(\overline{B C}\) માપો.
ઉત્તરઃ

પક્ષ: AB = 7.8 સેમી અને AC = 4.7 સેમી
- રેખા l રચો. રેખા l પર કોઈ પણ જગ્યાએ બિંદુ A નક્કી કરો.
- પરિકરની અણી માપપટ્ટીના શૂન્ય ઉપર અને પેન્સિલની અણી 7.8 સેમી દર્શાવતા અંક પર મૂકો.
- પરિકરનું માપ ન બદલાય તે રીતે પરિકરની અણી બિંદુ A ઉપર મૂકી રેખા l ઉપર ચાપ દોરો. આ ચાપના છેદબિંદુને B કહો.
- \(\overline{A B}\) એ 7.8 સેમીનો રેખાખંડ છે.
હવે, \(\overline{A B}\)માંથી 4.7 સેમીનો AC કાપવા માટે - પરિકરની અણી માપપટ્ટીના શૂન્ય ઉપર અને પેન્સિલની અણી 4.7 સેમી દર્શાવતા અંક પર મૂકો.
- પરિકરનું માપ ન બદલાય તે રીતે પરિકરની અણી બિંદુ A ઉપર મૂકી રેખા l ઉપર ચાપ દોરો. આ ચાપના છેદબિંદુને C કહો.
\(\overline{B C}\)નું માપપટ્ટી વડે માપ લેતાં BC = 3.1 સેમી મળે છે.
![]()
પ્રશ્ન 4.
3.9 સેમી લંબાઈનો \(\overline{A B}\) આપેલો છે. \(\overline{P Q}\) એવો રચો કે જેની લંબાઈ \(\overline{A B}\)ની લંબાઈ કરતાં બે ગણી હોય. માપીને ચકાસો.

(સૂચન: \(\overline{P X}\) રચો. જેની લંબાઈ, \(\overline{A B}\)ની લંબાઈ જેટલી હોય. ત્યાર પછી \(\overline{X Q}\) રચો. જેની લંબાઈ પણ \(\overline{A B}\) જેટલી જ હોય.)
ઉત્તરઃ
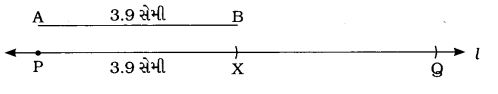
- AB = 3.9 સેમી લંબાઈનો \(\overline{A B}\) આપેલ છે.
- રેખા l દોરો.
- રેખા l પર બિંદુ P લો. પરિકર વડે \(\overline{A B}\) જેટલું માપ લઈ પરિકરની
અણી બિંદુ P પર મૂકી રેખા l પર ચાપ દોરો. રેખા અને જ્યાં ચાપ છેદે તેને X કહો. PX = AB (= 3.9 સેમી) થશે. - હવે પરિકરનું માપ એટલું જ રાખી પરિકરની અણી બિંદુ X ઉપર મૂકી રેખા l પર બીજો ચાપ જમણી બાજુ દોરો. રેખા lને આ ચાપ જ્યાં છેદે તેને શુ કહો. XQ = AB (= 3.9 સેમી) થશે.
- આ રીતે \(\overline{P Q}\)ની લંબાઈ એ \(\overline{A B}\)ની લંબાઈ કરતાં બે ગણી થાય.
ચકાસણી AB + AB = 3.9 સેમી + 3.9 સેમી
∴ 2AB = 7.8 સેમી = PQ
આમ, \(\overline{A B}\)ની લંબાઈના બે ગણા એ \(\overline{P Q}\)ની લંબાઈ જેટલા છે.
![]()
પ્રશ્ન 5.
7.8 સેમી લંબાઈનો \(\overline{A B}\) અને 3.4 સેમી લંબાઈનો \(\overline{C D}\) આપેલ છે. \(\overline{A B}\) અને \(\overline{C D}\)ની લંબાઈના તફાવત જેટલો \(\overline{X Y}\) રચો. માપીને ચકાસો.
ઉત્તરઃ
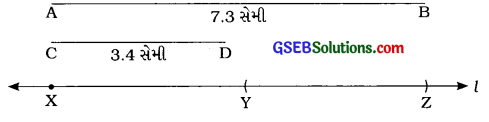
- AB = 7.3 સેમી અને CD = 3.4 સેમીના રેખાખંડ આપેલા છે.
- રેખા l દોરો અને તેના ઉપર બિંદુ X લો.
- પરિકરની અણી x ઉપર મૂકી AB = 7.3 સેમી જેટલું અંતર લઈ રેખા l ઉપર ચાપ દોરો. છેદબિંદુને Z કહો. XZ = AB = 7.3 સેમી થશે.
- પરિકરની અણી Z ઉપર મૂકી CD = 3.4 સેમી જેટલું અંતર લઈ રેખા l ઉપર ડાબી બાજુ ચાપ દોરો. છેદબિંદુને Y કહો.
ZY = CD = 3.4 સેમી થશે.
આ પ્રમાણે માગ્યા મુજબનો \(\overline{X Y}\) તૈયાર થાય.
ચકાસણી: XY = 7.3 સેમી – 3.4 સેમી = 3.9 સેમી
= AB – CD
આમ, XY = AB – CD