Gujarat Board GSEB Solutions Class 6 Maths Chapter 3 સંખ્યા સાથે Ex 3.7 Textbook Exercise Questions and Answers.
Gujarat Board Textbook Solutions Class 6 Maths Chapter 3 સંખ્યા સાથે Ex 3.7
પ્રશ્ન 1.
રેણુ 75 કિગ્રા અને 69 કિગ્રા વજનવાળી બે ખાતરની ગૂણી ખરીદે છે. ખાતરના આ વજનનું મહત્તમ મૂલ્ય શોધો કે જે બંને ગૂણીના વજનનું ગુણાંકમાં પૂરેપૂરું માપ લઈ શકે છે.
જવાબ:
વધુમાં વધુ કેટલું વજન હોઈ શકે તે શોધવા 75 કિગ્રા અને 69 કિગ્રાનો ગુ.સા.અ. શોધીશું.
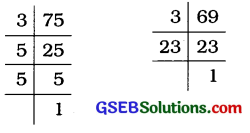
75ના અવિભાજ્ય અવયવો = 3 × 5 × 5,
69ના અવિભાજ્ય અવયવો = 3 × 23
75 અને 69ના સામાન્ય અવિભાજ્ય અવયવ = 3
∴ 75 અને 69નો ગુ.સા.અ. = 3
∴ માગ્યા મુજબ મહત્તમ વજનનું મૂલ્ય 3 કિગ્રા છે.
પ્રશ્ન 2.
૩ છોકરાઓ એક જ જગ્યાએથી એકસાથે પગ ઉપાડી ચાલવાની શરૂઆત કરે છે. એમનાં પગલાંનું માપ અનુક્રમે 63 સેમી, 70 સેમી અને 77 સેમી છે. એમાંથી દરેક કેટલું લઘુતમ અંતર નક્કી કરે છે જે અંતર પૂરેપૂરું પગલાંમાં નિશ્ચિત થઈ જાય.
જવાબ:
દરેક બાળકે લઘુતમ કેટલું અંતર ચાલવું તે શોધવા લ.સા.અ. શોધવો પડે. આથી આપણે 63 સેમી, 70 સેમી અને 77 સેમીનો લ.સા.અ. શોધીશું.
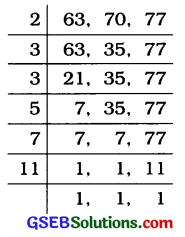
63, 70 અને 77નો. લ.સા.અ.
= 2 × 3 × 3 × 5 × 7 × 11 = 6930
આથી જરૂરી લઘુતમ અંતર 6930 સેમી છે.
પ્રશ્ન 3.
કોઈ ઓરડાની લંબાઈ, પહોળાઈ અને ઊંચાઈ અનુક્રમે 825 સેમી, 675 સેમી અને 450 સેમી છે. એવી સૌથી લાંબી ટેપ શોધો જે ઓરડાની ત્રણેય બાજુઓને પૂરેપૂરું માપી લે.
જવાબ:
ત્રણે બાજુઓનું માપ માપી શકે તેવી સૌથી મોટી ટેપ શોધવા માટે આપણે 825 સેમી, 675 સેમી અને 450 સેમીનો ગુ.સા.અ. શોધીશું.
825ના અવયવો = 3 × 5 × 5 × 11
675ના અવયવો = 3 × 3 × 3 × 5 × 5
450ના અવયવો = 2 × 3 × 3 × 5 × 5
∴ 825, 675 અને 450ના સામાન્ય અવયવો = 3 × 5 × 5
∴ 825, 675 અને 450નો ગુ.સા.અ. = 3 × 5 × 5 = 75
આમ, જરૂરી મોટામાં મોટી ટેપ 75 સેમીની જોઈએ.
પ્રશ્ન 4.
6, 8 અને 12થી વિભાજ્ય ત્રણ અંકોની સૌથી નાની સંખ્યા શોધો.
જવાબ:
અહીં સૌપ્રથમ આપણે 6, 8 અને 12નો લ.સા.અ. શોધીશું.
∴ 6, 8 અને 12નો લ.સા.અ. = 2 ×2 × 2 × 3 = 24
હવે, ત્રણ અંકોની સૌથી નાની સંખ્યા 100 છે.
100ને ઉપરના લ.સા.અ. વડે ભાગતાં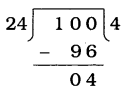 
શેષ 4 મળે.
હવે, જરૂરી ત્રણ અંકોની નાનામાં નાની સંખ્યા જેને 24 વડે નિઃશેષ ભાગી શકાય. = ત્રણ અંકની નાનામાં નાની સંખ્યા – શેષ + લ.સા.અ.
= (100 – 4) + 24
= 96 + 24 = 120
આમ, માગ્યા મુજબની નાનામાં નાની સંખ્યા 120 છે.
પ્રશ્ન 5.
8, 10 અને 12થી વિભાજ્ય ત્રણ અંકોની સૌથી મોટી સંખ્યા શોધો.
જવાબ:
અહીં સૌપ્રથમ આપણે 8, 10 અને 12નો લ.સા.અ. શોધીશું.
8, 10 અને 12નો લ.સા.અ.
= 2 × 2 × 2 × 3 × 5
= 120
આપણે જાણીએ છીએ કે ત્રણ અંકોની મોટામાં મોટી સંખ્યા 999 છે.
999ને 120 વડે ભાગતાં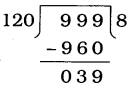 
શેષ 39 મળે.
હવે, માગ્યા મુજબની ત્રણ અંકોની સંખ્યા જેને 120 વડે નિઃશેષ ભાગી શકાય. = ત્રણ અંકોની સૌથી મોટી સંખ્યા – શેષ = 999 -39 = 960
આમ, માગ્યા મુજબની સંખ્યા 960 છે.
પ્રશ્ન 6.
જુદા જુદા રસ્તાની 3 ટ્રાફિક લાઈટ અનુક્રમે દરેક 48 સેકન્ડ, 72 સેકન્ડ, 108 સેકન્ડ પછી બદલાય છે. જો તે એકસાથે સવારે 7 વાગે બદલાય, તો તે ફરીથી એકસાથે ક્યારે બદલાશે?
જવાબ:
અહીં ટ્રાફિક સિગ્નલની લાઇટોની સમય અવધી 48 સેકન્ડ, 72 સેકન્ડ અને 108 સેકન્ડ છે. પહેલાં 48, 72 અને 108નો લ.સા.અ. શોધીએ.
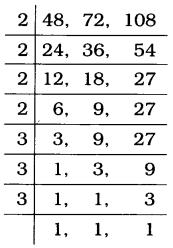
48, 72 અને 108નો લ.સા.અ.
= 2 × 2 × 2 × 2 × 3 × 3 × 3 = 432
હવે, 432 સેકન્ડ = \(\frac{432}{60}\) મિનિટ
= 7 મિનિટ 12 સેકન્ડ
આથી લાઇટ ફરી બદલાવાનો સમય સવારે
7 વાગ્યા પછી 7 મિનિટ 12 સેકન્ડ એટલે કે
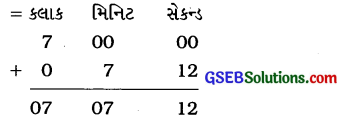
માગ્યા મુજબનો જવાબ સવારે 7 વાગ્યા પછી 7 મિનિટ 12 સેકન્ડ
પ્રશ્ન 7.
ત્રણ ટેન્કરોમાં અનુક્રમે 403 લિટર, 434 લિટર અને 465 લિટર ડીઝલ છે. આ સાધનની મહત્તમ ધારણશક્તિ (સમર્થતા) શોધો કે જે આ ત્રણેય ટેન્કરોના ડીઝલને પૂરેપૂરું ગુણાંકમાં માપી શકે.
જવાબ:
અહીં ત્રણે ટેન્કરોની ડીઝલની મહત્તમ ધારણશક્તિ (સમર્થતા) શોધવા માટે 403 લિટર, 434 લિટર અને 465 લિટરનો ગુ.સા.અ. શોધીશું.
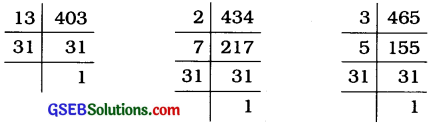
403ના બધા અવિભાજ્ય અવયવો = 13 × 31
434ના બધા અવિભાજ્ય અવયવો = 2 × 7× 31
465ના બધા અવિભાજ્ય અવયવો = 3 × 5 × 31
∴ 403, 434 અને 465ના સામાન્ય અવિભાજ્ય અવયવ = 31
આમ, સાધનની મહત્તમ ધારણશક્તિ 31 લિટર હોય.
પ્રશ્ન 8.
એવી સૌથી નાની સંખ્યા શોધો કે જેને 6, 15 અને 18થી ભાગવાથી દરેક સ્થિતિમાં 5 શેષ રહે.
જવાબ:
અહીં સૌપ્રથમ આપણે 6, 15 અને 18નો લ.સા.અ. શોધીશું. (સૌથી નાની સંખ્યા)
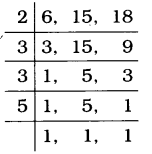
6, 15 અને 18નો લ.સા.અ.
= 2 × 3 × 3 × 5 = 90
6, 15 અને 18થી ભાગતાં શેષ 5 રહે તેવી સંખ્યા શોધવાની છે.
∴ માગ્યા મુજબની સંખ્યા = લ.સા.અ. + શેષ
= 90 + 5 = 95.
માગ્યા મુજબની સંખ્યા 95 છે.
પ્રશ્ન 9.
ચાર અંકોની એવી સૌથી નાની સંખ્યા શોધો જે 18, 24 અને 32થી વિભાજ્ય છે.
જવાબ:
સૌથી નાની સંખ્યા શોધવા આપેલી સંખ્યાઓનો લ.સા.અ. શોધવો પડે. અહીં સૌપ્રથમ આપણે 18, 24 અને 32નો લ.સા.અ. શોધીશું.
હવે ચાર અંકોની નાનામાં નાની સંખ્યા 1000 છે.
1000ને 288 વડે ભાગતાં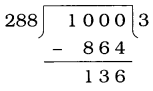 
શેષ 136 મળે.
∴ 18, 24 અને 32 વડે નિઃશેષ ભાગી શકાય તેવી નાનામાં નાની ચાર અંકોની સંખ્યા = 1000 – 136 + 288 = 1152
નોંધ: 1000માંથી 136 બાદ કરતાં મળતી સંખ્યા ત્રણ અંકોની થઈ જાય. તેથી તેમાં 288 ઉમેરવા પડે અને સંખ્યા ચાર અંકોની મળે.
પ્રશ્ન 10.
નીચે આપેલી સંખ્યાઓનો લ.સા.અ. શોધોઃ
(a) 9 અને 4
(b) 12 અને 5
(c) 6 અને 5
(d) 15 અને 4
લ.સા.અ. શોધવાની પદ્ધતિમાં તમને સામાન્ય શું જણાયું? શું દરેક કિસ્સામાં તે બે સંખ્યાનો ગુણાકાર છે?
જવાબ:
(a) 9 અને 4
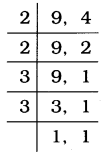
9 અને 4નો લ.સા.અ. = 2 × 2 × 3 × 3 = 36
વળી, 9 અને 4નો ગુણાકાર = 9 × 4 = 36
∴ 9 અને 4નો લ.સા.અ.
= 9 અને 4નો ગુણાકાર
(b) 12 અને 5
12 અને 5નો લ.સા.અ. = 2 × 2 ×3 × 5 = 60
વળી, 12 અને 5નો ગુણાકાર = 12 * 5 = 60
∴ 12 અને 5નો લ.સા.અ.
= 12 અને 5નો ગુણાકાર
(c) 6 અને 5
6 અને 5નો લ.સા.અ. = 2 × 3 × 5 = 30
વળી, 6 અને 5નો ગુણાકાર = 6 × 5 = 30
∴ 6 અને 5નો લ.સા.અ.
= 6 અને 5નો ગુણાકાર
(d) 15 અને 4
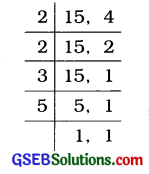
15 અને 4નો લ.સા.અ. = 2 × 2 × 3 × 5 = 60
વળી, 15 અને 4નો ગુણાકાર = 15 × 4 = 60
∴ 15 અને 4નો લ.સા.અ.
= 15 અને 4નો ગુણાકાર
આગળ બધા દાખલામાં લ.સા.અ. શોધતાં જણાય છે કે દરેક લ.સા.અ. એ 2 અને 3 બંનેનો ગુણક છે. વળી, દરેકમાં મળતો લ.સા.અ. એ આપેલી સંખ્યાઓનો ગુણાકાર જેટલો છે.
પ્રશ્ન 11.
નીચે આપેલ સંખ્યાઓનો લ.સા.અ. શોધો કે જેમાં એક સંખ્યા બીજી સંખ્યાનો અવયવ હોય?
(a) 5, 20
(b) 6, 18
(c) 12, 48
(d) 9, 45.
જવાબ:
(a) 5, 20
(b) 6, 18
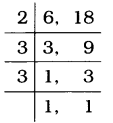
∴ 6 અને 18નો લ.સા.અ. = 2 × 3 × 3
= 18
(c) 12, 48
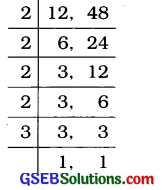
∴ 12 અને 48નો લ.સા.અ. 2 6, 24
= 2 × 2 × 2 × 2 × 3
= 48
(d) 9, 45
∴ 9 અને 45નો લ.સા.અ. = 3 × 3 × 5
= 45.
આગળના દરેક દાખલામાં મળતો લ.સા.અ. એ આપેલી બે સંખ્યાઓમાંની મોટી સંખ્યા જેટલો છે. આમ બનવાનું કારણ એ છે કે નાની સંખ્યા માં મોટી સંખ્યાનો અવયવ છે.
[નોંધઃ આપેલી બે સંખ્યામાં નાની સંખ્યા માં મોટી સંખ્યાનો અવયવ હોય, તો તે બે સંખ્યાનો લ.સા.અ. એ મોટી સંખ્યા જ હોય. વળી આ બે સંખ્યાઓનો ગુ.સા.અ. એ નાની સંખ્યા જ હોય.]