Gujarat Board GSEB Solutions Class 8 Maths Chapter 8 રાશિઓની તુલના InText Questions and Answers.
Gujarat Board Textbook Solutions Class 8 Maths Chapter 8 રાશિઓની તુલના InText Questions
પ્રયત્ન કરો : (પાઠ્યપુસ્તક પાન નંબ 119)
એક પ્રાથમિક શાળાના વિદ્યાર્થીઓના વાલીઓને પૂછવામાં આવ્યું કે તેઓ એક દિવસમાં કેટલા કલાક તેઓનાં બાળકોને ગૃહકાર્યમાં મદદ કરે છે?
90 વાલીઓ એવા હતા કે જેઓ પોતાનાં બાળકને \(\frac {1}{2}\)થી 1\(\frac {1}{2}\) કલાક મદદ કરે છે. નીચેની આકૃતિમાં વાલીઓ પોતાનાં બાળકને મદદ કરવા જે સમય ફાળવે છે, તેના પરથી તેઓનું (વાલીની સંખ્યાનું) વિભાજન કરેલ છે.
20 % વાલીઓ 1\(\frac {1}{2}\) કલાકથી વધારે સમય મદદ કરે છે, 30 % વાલીઓ \(\frac {1}{2}\) થી 1\(\frac {1}{2}\) કલાક મદદ કરે છે અને 50 % વાલીઓ મદદ નથી કરતા.
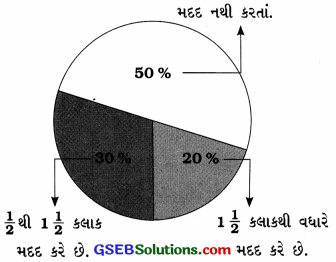
આ પરથી નીચેના પ્રશ્નોના જવાબ આપોઃ
પ્રશ્ન (i).
કુલ કેટલા વાલીઓને પૂછવામાં આવ્યું હતું?
ઉત્તરઃ
90 વાલીઓ પોતાનાં બાળકને \(\frac {1}{2}\) કલાકથી 1\(\frac {1}{2}\) કલાક ગૃહકાર્યમાં મદદ કરે છે.
પાઈ-ચાર્ટમાં આપેલી ટકાવારી = 30 %
ધારો કે સર્વે કરવામાં આવેલી વ્યક્તિઓ x છે.
આમ, xના 30 % વાલીઓ પોતાનાં બાળકને \(\frac {1}{2}\) કલાકથી 1\(\frac {1}{2}\) કલાક ગૃહકાર્યમાં મદદ કરે છે.
∴ xના 30 % = 90
∴ x × \(\frac {30}{100}\) = 90
∴ x = \(\frac{90 \times 100}{30}\)
∴ x = 300
આમ, 300 વાલીઓને પૂછવામાં આવ્યું હતું.
પ્રશ્ન (ii).
કેટલા વાલીઓ મદદ જ નહોતા કરતા?
ઉત્તરઃ
50 % વાલીઓ પોતાનાં બાળકને ગૃહકાર્યમાં મદદ કરતા નથી.
∴ 300ના 50 % વાલીઓ પોતાનાં બાળકને ગૃહકાર્યમાં મદદ કરતા નથી.
∴ વાલીઓની આ સંખ્યા = 300 × \(\frac {50}{100}\)
= 3 × 50 = 150
આમ, 150 વાલીઓ પોતાનાં બાળકને ગૃહકાર્યમાં મદદ નહોતા કરતા.
પ્રશ્ન (iii).
કેટલા વાલીઓ 1\(\frac {1}{2}\) કલાકથી વધારે સમય મદદ કરતા હતા?
ઉત્તરઃ
20 % વાલીઓ પોતાનાં બાળકને 1\(\frac {1}{2}\) કલાકથી વધારે સમય ગૃહકાર્યમાં મદદ કરતા હતા.
∴ 300ના 20 % વાલીઓ પોતાનાં બાળકને 1\(\frac {1}{2}\) કલાકથી વધારે સમય ગૃહકાર્યમાં મદદ કરતા હતા.
∴ વાલીઓની આ સંખ્યા = 300 × \(\frac {20}{100}\)
= 3 × 20 = 60
આમ, 60 વાલીઓ પોતાનાં બાળકને 1\(\frac {1}{2}\) કલાકથી વધારે સમય ગૃહકાર્યમાં મદદ કરતા હતા.
![]()
પ્રયત્ન કરો (પાઠ્યપુસ્તક પાન નંબ 121)
1. એક દુકાનદાર 20 % વળતર આપે છે, તો નીચે આપેલી વસ્તુઓની વેચાણકિંમત શું હશે?
(a) એક ડ્રેસ જેની છાપેલી કિંમત ₹ 120 છે.
ઉત્તરઃ
ડ્રેસની છાપેલી કિંમત = ₹ 120
વળતરની ટકાવારી = 20 %
∴ ડ્રેસની ખરીદીમાં મળતું વળતર = ₹ 120ના 20 %
= ₹ (120 × \(\frac {20}{100}\)) = ₹ 24
∴ ડ્રેસની વેચાણકિંમત = ડ્રેસની છાપેલી કિંમત – વળતર
= ₹ (120 – 24) = ₹ 96
આમ, ડ્રેસની વેચાણકિંમત ₹ 96 છે.
(b) એક જોડી બૂટ જેની છાપેલી કિંમત ₹ 750 છે.
ઉત્તરઃ
બૂટની છાપેલી કિંમત = ₹ 750
વળતરની ટકાવારી = 20 %
∴ બૂટની ખરીદીમાં મળતું વળતર = ₹ 750ના 20 %
= ₹ (750 × \(\frac {20}{100}\)) = ₹ 150
∴ બૂટની વેચાણકિંમત = બૂટની છાપેલી કિંમત – વળતર
= ₹ (750 – 150) = ₹ 600
આમ, બૂટની વેચાણકિંમત ₹ 600 છે.
(c) એક થેલો જેની છાપેલી કિંમત ₹ 250 છે.
ઉત્તરઃ
થેલાની છાપેલી કિંમત = ₹ 250
વળતરની ટકાવારી = 20 %
∴ થેલાની ખરીદીમાં મળતું વળતર = ₹ 250ના 20 %
= ₹ (250 × \(\frac {20}{100}\)) = ₹ 50
∴ થેલાની વેચાણકિંમત = થેલાની છાપેલી કિંમત – વળતર
= ₹ (250 – 50) = ₹ 200
આમ, થેલાની વેચાણકિંમત ₹ 200 છે.
![]()
2. એક ટેબલ જેની છાપેલી કિંમત ₹ 15,000 છે, તે ₹ 14,400માં મળે છે. તેના પર મળેલ વળતર અને વળતરની ટકાવારી શોધો.
ઉત્તરઃ
ટેબલની છાપેલી કિંમત = ₹ 15,000
ટેબલની વેચાણકિંમત = ₹ 14,400
∴ ટેબલની ખરીદીમાં મળતું વળતર = છાપેલી કિંમત – વેચાણકિંમત
= ₹ (15,000 – 14,400)
= ₹ 600
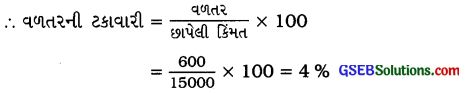
ટેબલના વેચાણમાં વળતર ₹ 600 અને વળતરની ટકાવારી 4 % છે.
3. એક કબાટ 5 % વળતર આપી ₹ 5,225માં વેચેલ છે, તો તેની છાપેલા કિંમત શોધો.
ઉત્તરઃ
કબાટની વેચાણકિંમત = ₹ 5225
વળતરની ટકાવારી = 5 %
∴ ₹ 100ની છાપેલી કિંમત પર મળતું વળતર = ₹ 5
∴ વેચાણકિંમત = ₹ (100 – 5)
= ₹ 95
₹ 95ની વેકિં. હોય, તો છાપેલી કિંમત = ₹ 100
∴ ₹ 5225 વે.કિ. હોય, તો છાપેલી કિંમત = ₹ (100 × \(\frac {5225}{95}\))
= ₹ 5500
આમ, કબાટની છાપેલી કિંમત ₹ 5500 છે.
![]()
પ્રયત્ન કરો (પાઠ્યપુસ્તક પાન નંબ 123)
જો 5% નફો થતો હોય, તો નીચેની વિગતો માટે વેચાણકિંમત શોધોઃ
(a) ₹ 700ની એક સાઈકલ, ₹ 50ના વધારાના ખર્ચ સાથે.
ઉત્તરઃ
સાઈકલની કિંમત = ₹ 700
અને અન્ય ખર્ચ = ₹ 50
∴ સાઇકલની પડતર કિંમત = સાઈકલની કિંમત + અન્ય ખર્ચ
= ₹ (700 + 50) = ₹ 750
નફાની ટકાવારી = 5 %
∴ નફો = પડતર કિંમત × નફાની ટકાવારી
= ₹ 750ના 5 %
= ₹ (750 × \(\frac {5}{100}\))
= ₹ \(\frac {3750}{100}\)
= ₹ 37.50
હવે, સાઇકલની વેકિં. = પડતર કિંમત + નફો
= ₹ (750 + 37.50) = ₹ 787.50
આમ, સાઇકલની વેકિં. ₹ 787.50 છે.
(b) ₹ 150માં ખરીદેલ ઘાસ કાપવાનું મશીન ₹ 50ના પરિવહન ખર્ચ સાથે.
ઉત્તરઃ
ઘાસ કાપવાના મશીનની કિંમત = ₹ 1150
અને પરિવહન ખર્ચ = ₹ 50
ઘાસ કાપવાના મશીનની પડતર કિંમત = ₹ (1150 + 50)
= ₹ 1200
નફાની ટકાવારી = 5 %
∴ નફો = પડતર કિંમતના 5 %
= ₹ 1200ના 5 %
= ₹ (1200 × \(\frac {5}{100}\)) = ₹ 60
∴ ઘાસ કાપવાના મશીનની વેકિં. = પડતર કિંમત + નફો
= ₹ (1200 + 60) = ₹ 1260
આમ, ઘાસ કાપવાના મશીનની વેકિં. ₹ 1260 છે.
(c) ₹ 560માં ખરીદેલ પંખો, ₹ 40ના સમારકામના વધારાના ખર્ચ સાથે.
ઉત્તરઃ
પંખાની કિંમત = ₹ 560
સમારકામનો ખર્ચ = ₹ 40
∴ પંખાની પડતર કિંમત = ₹ (560 + 40) = ₹ 600
નફાની ટકાવારી = 5 %
∴ નફો = પડતર કિંમતના 5 %
= ₹ 600ના 5 %
= ₹ (600 × \(\frac {5}{100}\))
= 30
∴ પંખાની વે,કિં = પડતર કિંમત + નફો
= ₹ (600 + 30) = ₹ 630
આમ, પંખાની વેકિં. ₹ 630 છે.
![]()
પ્રયત્ન કરો (પાઠ્યપુસ્તક પાન નંબ 123)
એક દુકાનદારે દરેકના ₹ 10,000 લેખે બે ટીવી (TV) ખરીદ્યાં. તે પૈકી એક 10%ના નફા સાથે અને બીજું 10%ની ખોટ સાથે વેચે છે. તેને સમગ્ર રીતે નફો થયો કે ખોટ તે શોધો.
ઉત્તરઃ
દુકાનદારે બે ટીવી ખરીદ્યાં છે. દરેક ટીવીની ખરીદ કિંમત ₹ 10,000 છે.
∴ દુકાનદારની કુલ પડતર કિંમત = 2 × ₹ 10,000 = ₹ 20,000
દુકાનદારે પહેલું ટીવી 10 % નફાથી વેચ્યું છે.
∴ નફો = ₹ 10,000ના 10 %
= ₹ (10000 × \(\frac {10}{100}\)) = ₹ 1000
∴ પહેલા ટીવીની વેકિં. = પડતર કિંમત + નફો
= ₹ (10,000 + 1000) = ₹ 11,000
દુકાનદારે બીજું ટીવી 10 % ખોટ સાથે વેચ્યું છે.
∴ ખોટ = ₹ 10,000ના 10 %
= ₹ (10000 × \(\frac {10}{100}\)) = ₹ 1000
∴ બીજા ટીવીની વે,કિં. = પડતર કિંમત – ખોટ
= ₹ (10,000 – 1000) = ₹ 9000
બંને ટીવીની વેકિં. = ₹ (11,000 + 9000)
= ₹ 20,000
આમ, બંને ટીવીની પડતર કિંમત = બંને ટીવીની વેચાણકિંમત
આમ, વેપારીને એકંદરે નફો કે ખોટ થતા નથી.
વિચારો, ચર્ચા કરો અને લખો (પાઠ્યપુસ્તક પાન નંબ 125)
1. કોઈ સંખ્યાની બમણી સંખ્યા એ 100 %નો વધારો છે. જો આપણે તે સંખ્યાનો અડધો ભાગ લઈએ, તો ટકાવારીમાં કેટલો ઘટાડો હશે?
ઉત્તરઃ
ધારો કે તે સંખ્યા x છે. આ સંખ્યાના અડધા \(\frac{x}{2}\) થાય.
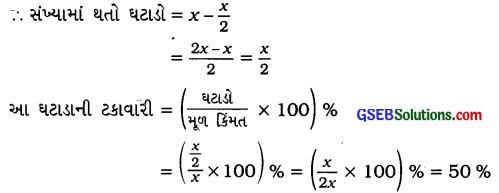
આમ, ટકાવારીમાં 50 %નો ઘટાડો થશે.
2. ₹ 2000 એ ₹ 2400 કરતાં કેટલા ટકા ઓછા છે? ₹ 2400 એ ₹ 2000 કરતાં ટકાવારીમાં કેટલા વધુ છે? શું બંને ફેરફાર સમાન છે?
ઉત્તરઃ
(a) અહીં ₹ 2400 કિંમતને ઘટાડીને ₹ 2000 કરવામાં આવે છે.
મૂળ કિંમત = ₹ 2400, નવી કિંમત = ₹ 2000
∴ કરાયેલો ઘટાડો = ₹ (2400 – 2000) = ₹ 400

આમ, ઘટાડો 16\(\frac {2}{3}\) % છે.
(b) અહીં ₹ 2000 કિંમતને વધારીને ₹ 2400 કરવામાં આવે છે.
મૂળ કિંમત = ₹ 2000, નવી કિંમત = ₹ 2400
કરાયેલો વધારો = ₹ (2400 – 2000) = ₹ 400

આમ, વધારાના 20 % છે.
ટૂંકમાં ઘટાડાની ટકાવારી અને વધારાની ટકાવારી સરખી નથી.
![]()
પ્રયત્ન કરો (પાઠ્યપુસ્તક પાન નંબ 126)
₹ 15,000નું 5 % પ્રતિ વર્ષ વ્યાજ લેખે 2 વર્ષનું વ્યાજ અને વ્યાજમુદ્દલ શોધો.
ઉત્તરઃ
અહીં મુદ્દલ (P) = ₹ 15,000; વ્યાજનો દર (R) = 5 %, મુદત (T) = 2 વર્ષ
SI = \(\frac{P \times R \times T}{100}\)
= \(\frac{15000 \times 5 \times 2}{100}\) = ₹ 1500
100 વ્યાજમુદ્દલ = મુદ્દલ + વ્યાજ
= ₹ (15,000 + 1500) = ₹ 16,500
અથવા
₹ 100નું 1 વર્ષનું વ્યાજ = ₹ 5
∴ ₹ 15,000નું 2 વર્ષનું વ્યાજ = ₹ \(\left(\frac{15000}{100} \times \frac{2}{1} \times \frac{5}{1}\right)\)
= ₹ 1500
વ્યાજમુદ્દલ = મુદ્દલ + વ્યાજ
= ₹ (15,000 + 1500) = ₹ 16,500
આમ, વ્યાજ ₹ 1500 અને વ્યાજમુદ્દલ ₹ 16,500
પ્રયત્ન કરો (પાઠ્યપુસ્તક પાન નંબ 129)
1. ₹ 8000 પર 5% પ્રતિ વર્ષ વ્યાજ દરે 2 વર્ષ માટે ચક્રવૃદ્ધિ વ્યાજ શોધો.
ઉત્તરઃ
અહીં મુદ્દલ (P) = ₹ 8000; વ્યાજનો દર (R) = 5 %, મુદત (T) = 2 વર્ષ
A = \(P\left(1+\frac{R}{100}\right)^{n}\)
= \(8000\left(1+\frac{5}{100}\right)^{2}\)
= \(8000\left(\frac{100+5}{100}\right)^{2}\)
= \(8000\left(\frac{105}{100}\right)^{2}\)
= \(8000 \times \frac{105}{100} \times \frac{105}{100}\)
= 8820
આમ, વ્યાજમુદ્દલ = ₹ 8820
∴ ચક્રવૃદ્ધિ વ્યાજ = વ્યાજમુદ્દલ – મુદ્દલ
= ₹ 8820 – 8000 = ₹ 820
આમ, ચક્રવૃદ્ધિ વ્યાજ CI = ₹ 820
![]()
પ્રયત્ન કરો (પાઠ્યપુસ્તક પાન નંબ 130)
સમયગાળો અને દર શોધોઃ
1. એક રકમ 1\(\frac {1}{2}\) વર્ષ માટે 8%ના દરે અર્ધવાર્ષિક ચક્રવૃદ્ધિ વ્યાજે લેવામાં આવે છે.
ઉત્તરઃ
અહીં મુદત (T) = 1\(\frac {1}{2}\) વર્ષ = \(\frac {3}{2}\) વર્ષ અને વ્યાજનો દર R = 8%
આમ, સમયગાળો n = 1\(\frac {1}{2}\) × 2 = \(\frac {3}{2}\) × 2 = 3
અને વ્યાજનો દર (R) = \(\frac {8}{2}\)% = 4%
2. એક રકમ 2 વર્ષ માટે 4%ના દરે અર્ધવાર્ષિક ચક્રવૃદ્ધિ વ્યાજે લેવામાં આવે છે.
ઉત્તરઃ
અહીં મુદત (T) = 2 વર્ષ અને વ્યાજનો દર (R) = 4 %
આમ, સમયગાળો (n) = 2 × 2 = 4
અને વ્યાજનો દર R = \(\frac {4}{2}\) % = 2 %
વિચારો, ચર્ચા કરો અને લખો (પાઠ્યપુસ્તક પાન નંબ 130)
એક રકમ એક વર્ષ માટે 16 % પ્રતિ વર્ષના દરે લેવામાં આવેલ છે. ચક્રવૃદ્ધિ વ્યાજ દરનો સમય ત્રિમાસિક હોય, તો એક વર્ષમાં કેટલી વાર વ્યાજની ગણતરી કરવામાં આવશે?
ઉત્તરઃ
અહીં વ્યાજની ગણતરી ચક્રવૃદ્ધિ વ્યાજની રીતે કરવાની છે.
વ્યાજની ગણતરી ત્રિમાસિક કરવાની છે. એટલે કે વર્ષમાં 4 વખતે થાય.
આમ, વ્યાજનો દર = \(\frac {16}{4}\) % = 4 %
આમ, વ્યાજની ગણતરી ત્રિમાસિક થતી હોઈ એક વર્ષમાં વ્યાજની ગણતરી 4 વખત થાય.
![]()
પ્રયત્ન કરો (પાઠ્યપુસ્તક પાન નંબ 131)
ચૂક્વવાની રકમ શોધોઃ
1. ₹ 2400નું 2 વર્ષના અંતે 5%ના વાર્ષિક દરે ચક્રવૃદ્ધિ વ્યાજ
ઉત્તરઃ
અહીં મુદ્દલ (P) = ₹ 2400, મુદત (n) = 2 વર્ષ, વ્યાજનો દર (R) = 5 % છે. ધ્યાનમાં રાખીશું કે વ્યાજની ગણતરી વાર્ષિક દરે કરવાની છે.
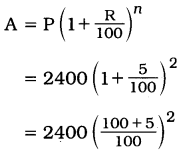

આમ, ચૂકવવાની રકમ ₹ 2646
2. ₹ 1800નું 1 વર્ષના અંતે 8%ના ત્રિમાસિક દરે ચક્રવૃદ્ધિ વ્યાજ
ઉત્તરઃ
અહીં વ્યાજની ગણતરી ત્રિમાસિક એટલે કે વર્ષમાં દર ત્રણ માસે કરવાની છે એટલે કે વર્ષમાં ચાર વખત વ્યાજની ગણતરી થાય.
મુદ્દલ (P) = ₹ 1800, વ્યાજનો દર (R) = \(\frac {8}{4}\) = 2 %,
મુદત (T) = 1 વર્ષ
n = 4 × 1 = 4


આમ, ચૂકવવાની રકમ ₹ 1948.38
![]()
પ્રયત્ન કરો : (પાઠ્યપુસ્તક પાન નંબ 133)
1. ₹ 10,500ની યંત્રસામગ્રીમાં 5%નો ઘટાડો થયો, તો એક વર્ષ પછી તેની કિંમત શોધો.
ઉત્તરઃ
અહીં P = ₹ 10,500; R = -5 %, T = 1 વર્ષ
∴ n = 1

આમ, ₹ 10,500 કિંમત 1 વર્ષને અંતે ₹ 9975 થાય.
2. એક શહેરની હાલની જનસંખ્યા 12 લાખ છે, તેમાં પ્રતિ વર્ષ 4%નો વધારો થાય છે, તો બે વર્ષ પછી શહેરની જનસંખ્યા શોધો.
ઉત્તરઃ
અહીં P = 12,00,000; જનસંખ્યામાં વધારો R = 4%,
મુદત (T) = 2 વર્ષ અહીં, n = 2

આમ, શહેરની જનસંખ્યા 2 વર્ષ પછી 12,97,920 થાય.