Gujarat Board GSEB Solutions Class 10 Maths Chapter 9 ત્રિકોણમિતિના ઉપયોગો Ex 9.1 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 10 Maths Chapter 9 ત્રિકોણમિતિના ઉપયોગો Ex 9.1
પ્રશ્ન 1.
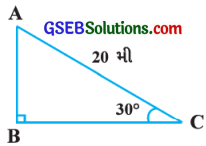
સર્કસના તંબુમાં, જમીન સાથે શિરોલંબ સ્થિતિમાં રહેલા થાંભલાની ટોચથી જમીન સાથે ખેંચીને બાંધેલા 20 મી લાંબા દોરડા પર એક કલાકાર ચડી રહ્યો છે. જો દોરડું જમીન સાથે 30° માપનો ખૂણો બનાવે, તો થાંભલાની ઊંચાઈ શોધો. (જુઓ આકૃતિ).
ઉત્તરઃ
અહીં, AB થાંભલો અને AC દોરડું દર્શાવે છે.
આથી ∆ ABCમાં, ∠B = 90°; ∠C = 30° અને ૨ AC = 20 મી.
હવે, sin C = \(\frac{\mathrm{AB}}{\mathrm{AC}}\)
sin 30° = \(\frac{\mathrm{AB}}{20}\)
AB = 10
આમ, થાંભલાની ઊંચાઈ 10 મી છે.

પ્રશ્ન 2.
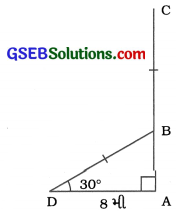
વાવાઝોડાને કારણે એક ઝાડ એ રીતે ભાંગીને વળી જાય છે, જેથી તેની ટોચ, જમીન સાથે 30° માપનો ખૂણો બનાવે તે રીતે જમીનને સ્પર્શે છે. ઝાડની જમીનને સ્પર્શતી ટોચ અને ઝાડના થડ વચ્ચેનું અંતર 8 મી હોય, તો ઝાડની ઊંચાઈ શોધો.
ઉત્તરઃ
અહીં, ઝાડ AC એ સ્થાન B આગળથી ભાંગીને એવી રીતે વળી જાય છે કે તેની ટોચ C જમીનને D બિંદુએ સ્પર્શે છે.
આથી ∆ BADHI, ∠A = 90°; ∠D = 30°; AD = 8 મી અને BC = BD.
હવે, tan D = \(\frac{\mathrm{BA}}{\mathrm{AD}}\)
tan 30° = \(\frac{\mathrm{BA}}{8}\)
\(\frac{1}{\sqrt{3}}=\frac{\mathrm{BA}}{8}\)∴ BA = \(\frac{8}{\sqrt{3}}\) મી,
વળી cos D = \(\frac{\mathrm{AD}}{\mathrm{BD}}\)
cos 30° = \(\frac{8}{\mathrm{BD}}\)
\(\frac{\sqrt{3}}{2}=\frac{8}{B D}\)∴ BD = \(\frac{16}{\sqrt{3}}\) મી
હવે, ઝાડની ઊંચાઈ = AC
= BA + BC = BA + BD
= \(\frac{8}{\sqrt{3}}+\frac{16}{\sqrt{3}}\)
= \(\frac{24}{\sqrt{3}}\)
= \(\frac{24}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}\)
= 8√3 મી આમ, ઝાડની ઊંચાઈ 8/3 મી છે.

પ્રશ્ન 3.
એક ઠેકેદારે બાળકોને રમવા માટે, બગીચામાં બે લપસણી લગાવવાની છે. આ માટે તે 5 વર્ષથી ઓછી ઉંમરનાં બાળકો માટે જમીનથી ઉપરનો છેડો 1.5 મી રહે અને જમીન સાથે 30નો ખૂણો બનાવે તેવી અને તેનાથી વધારે ઉંમરનાં બાળકો માટે 3 મીની ઊંચાઈથી સીધો ઢાળ હોય તથા જમીન સાથે છે 60નો ખૂણો બનાવતી હોય તેવી લપસણીઓ પસંદ કરે છે, તો બંને લપસણીઓની લંબાઈ શોધો.
ઉત્તરઃ
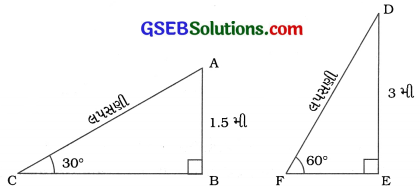
અહીં, AC એ 5 વર્ષથી ઓછી ઉંમરનાં બાળકો માટેની લપસણી દર્શાવે છે.
આથી ∆ ABCમાં, ∠B = 90°, ∠C = 30° અને ૨ AB = 1.5 મી.
હવે, sin C = \(\frac{\mathrm{AB}}{\mathrm{AC}}\)
∴ sin 30° = \(\frac{1.5}{\mathrm{AC}}\)
∴ \(\frac{1}{2}=\frac{1.5}{\mathrm{AC}}\)
∴ AC = 3 મી
તે જ રીતે, D એ 5 વર્ષથી વધારે ઉંમરનાં બાળકો માટેની લપસણી દર્શાવે છે.
આથી ∆ DEFમાં, ∠E = 90°; ∠F = 60° અને DE = 3 મી.
હવે, sin F = \(\frac{\mathrm{DE}}{\mathrm{DF}}\)
sin 60 = \(\frac{3}{\mathrm{DF}}\)
\(\frac{\sqrt{3}}{2}=\frac{3}{\mathrm{DF}}\)DF = \(\frac{3 \times 2}{\sqrt{3}}\)
DF = 2√3 મી આમ, 5 વર્ષથી ઓછી ઉંમરનાં બાળકો માટેની લપસણીની લંબાઈ 3મી અને તેનાથી વધારે ઉંમરનાં બાળકો માટેની લપસણીની લંબાઈ 2√3 મી થાય.

પ્રશ્ન 4.
ટાવરના પાયાથી 30 મી દૂર રહેલા જમીન પરના એક બિંદથી ટાવરની ટોચના ઉસેધકોણનું માપ 30° છે, તો ટાવરની ઊંચાઈ શોધો.
ઉત્તરઃ
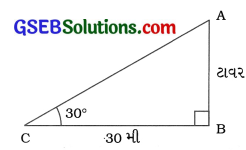
અહીં, AB એ ટાવર દર્શાવે છે. જેમાં A એ ટાવરની ટોચ છે અને બિંદુ C એ નિરીક્ષણ બિંદુ છે.
આથી ∆ ABCમાં, ∠B = 90°; ∠C = 30° અને BC = 30 મી.
હવે, cot C = \(\frac{\mathrm{BC}}{\mathrm{AB}}\)
cot 30 = \(\frac{30}{\mathrm{AB}}\)
√3 = \(\frac{30}{\mathrm{AB}}\)
∴ AB = \(\frac{30}{\sqrt{3}}\)
∴ AB = \(\frac{30}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}\)
AB = 10√3મી
આમ, ટાવરની ઊંચાઈ 10√3 મી છે.
નોંધઃ અહીં, આપણે tan Cનો ઉપયોગ પણ કરી શકીએ.

પ્રશ્ન 5.
એક પતંગ જમીનથી 60 મીની ઊંચાઈ પર ઊડી રહેલ છે. આ પતંગની દોરીનો એક છેડો ક્ષણભર માટે જમીન પરના એક બિંદુ સાથે બાંધેલ છે. આ સ્થિતિમાં દોરીનો જમીન સાથેનો ખૂણો 60° છે. જો દોરીમાં કોઈ ઢીલ નથી તેવું માની લેવામાં આવે, તો દોરીની લંબાઈ શોધો.
ઉત્તરઃ
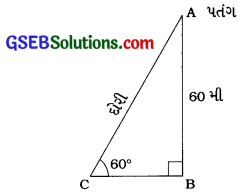
અહીં, A પતંગનું સ્થાન તથા AC ઢીલ વગરની દોરી દર્શાવે છે.
ધારો કે, AB એ સમથળ જમીનને લંબ છે.
આથી ∆ ABCમાં, ∠B = 90°; ∠C = 60° અને AB = 60 મી.
હવે, sin C = \(\frac{\mathrm{AB}}{\mathrm{AC}}\)
sin 60° = \(\frac{60}{\mathrm{AC}}\)
\(\frac{\sqrt{3}}{2}=\frac{60}{\mathrm{AC}}\)AC = \(\frac{60 \times 2}{\sqrt{3}}\)
AC = \(\frac{60 \times 2}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}\)
AC = 40√3 મી
આમ, દોરીની લંબાઈ 40√3 મી હોય.

પ્રશ્ન 6.
1.5 મી ઊંચો એક છોકરો એક 30 મી ઊંચી ઇમારતથી કોઈક અંતરે ઊભેલ છે. હવે જ્યારે તે ઇમારત તરફ ચાલવાનું શરૂ કરે છે ત્યારે કેટલાક સમય પછી તેની આંખથી ઇમારતની ટોચના ઉસેધકોણનું માપ 30થી વધીને 60° થાય છે, તો તે કેટલું અંતર ચાલ્યો હશે?
ઉત્તરઃ
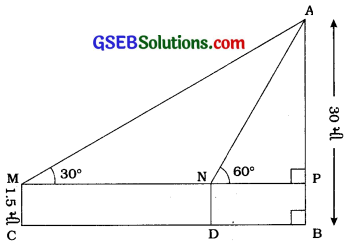
અહીં, AB ઇમારત દર્શાવે છે. C એ છોકરાનું શરૂઆતનું સ્થાન રે તથા D એ છોકરાનું અંતિમ સ્થાન દર્શાવે છે. વળી, M અને N એ બે સ્થાન પરની પરિસ્થિતિમાં છોકરાની આંખો દર્શાવે છે. ધારો કે, લંબાવેલ MN, ABP Pમાં મળે છે.
આથી ∆ APNમાં, ∠P = 90°; ∠N = 60° તથા ∆ APMમાં, ∠P = 90° અને ∠M = 30°.
વળી, CM = DN = BP = 1.5 મી અને
AP = AB – BP = 28.5 મી.
∆ APNમાં, ∠P = 90°
tan N = \(\frac{\mathrm{AP}}{\mathrm{PN}}\)
tan 60° = \(\frac{28.5}{\text { PN }}\)
√3 = \(\frac{28.5}{\text { PN }}\)
PN = \(\frac{28.5}{\sqrt{3}}\) મી
∆ APMમાં, ∠P = 90°
tan M = \(\frac{\mathrm{AP}}{\mathrm{PM}}\)
tan 30° = \(\frac{28.5}{\mathrm{PM}}\)
\(\frac{1}{\sqrt{3}}=\frac{28.5}{\mathrm{PM}}\)
∴ PM = 28.5√3મી
આથી છોકરાએ કાપેલ અંતર = CD
= MN = PM – PN = 28.5√3 – \(\frac{28.5}{\sqrt{3}}\)
= 28.5 (√3 – \(\frac{1}{\sqrt{3}}\))
= 28.5 (\(\left(\frac{3-1}{\sqrt{3}}\right)\))
= 28.5 × \(\frac{2}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}\)
= 9.5 × 2 × √3
= 19√3 મી આમ, છોકરો ઇમારતની દિશામાં 193 મી અંતર ચાલ્યો હશે.

પ્રશ્ન 7.
જમીન પર આવેલ એક બિંદુથી એક 20 મી ઊંચી ઇમારતની ટોચ પર રહેલ એક સંચાર ટાવરના તળિયા અને ટોચના ઉસેધકોણનાં જ માપ અનુક્રમે 45° અને 60° છે, તો ટાવરની ઊંચાઈ શોધો.
ઉત્તરઃ
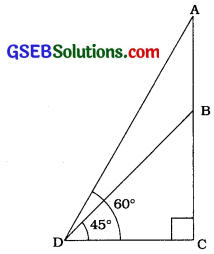
અહીં, AB સંચાર ટાવર, BC ઇમારત અને D નિરીક્ષણ બિંદુ દર્શાવે છે.
આથી ∆ BCDમાં, ∠C = 90°; ∠D = 45° અને BC = 20 મી તથા ∆ BCDમાં, ∠C = 90° અને ∠D = 60°.
∆ BCDમાં, ∠C = 90°
tan D = \(\frac{\mathrm{BC}}{\mathrm{CD}}\)
tan 45 = \(\frac{20}{\mathrm{CD}}\)
1 = \(\frac{20}{\mathrm{CD}}\)
CD = 20 મી
હવે, ∆ ACDમાં, ∠C = 90°
tan D = \(\frac{\mathrm{AC}}{\mathrm{CD}}\)
tan 60° = \(\frac{\mathrm{AC}}{20}\)
√3 = \(\frac{\mathrm{AC}}{20}\)
AC = 20√3 મી
હવે, સંચાર ટાવરની ઊંચાઈ = AB
= AC – BC = 20√3 – 20
= 20(√3 – 1) મી
આમ, સંચાર ટાવરની ઊંચાઈ 20 (√3 – 1) મી છે.

પ્રશ્ન 8.
એક ઊંચી બેઠક પર 1.6 મી ઊંચી એક પ્રતિમા ગોઠવેલ છે. જમીન પરના એક બિંદુએથી પ્રતિમાની ટોચના ઉન્સેધકોણનું માપ 60° અને બેઠકની ટોચના ઉસેધકોણનું માપ 45° છે, તો બેઠકની ઊંચાઈ શોધો.
ઉત્તરઃ
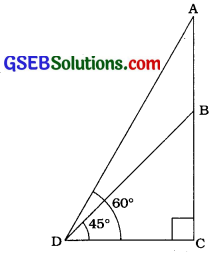
અહીં AB એ પ્રતિમા, BC એ બેઠક અને D એ જમીન પરનું નિરીક્ષણ બિંદુ દર્શાવે છે.
આથી ∆ BCDમાં, ∠C = 90° અને ∠D = 45° તથા ∆ ACDમાં, ∠C = 90° અને ∠D = 60°.
વળી, AB = પ્રતિમાની ઊંચાઈ = 1.6 મી.
ધારો કે, બેઠકની ઊંચાઈ BC = x મી.
હવે, ∆ BCDમાં, ∠C = 90°
tan D = \(\frac{\mathrm{BC}}{\mathrm{CD}}\)
tan 45° = \(\frac{x}{\mathrm{CD}}\)
∴ 1 = \(\frac{x}{\mathrm{CD}}\)
CD = x મી
∆ ACDમાં, ∠C = 90°
tan D = \(\frac{\mathrm{AC}}{\mathrm{CD}}\)
tan 60° = \(\frac{\mathrm{AC}}{x}\)
√3 = \(\frac{\mathrm{AC}}{x}\)
AC = √3x મી
હવે, AB = AC – BC
1.6 = √3x – x
1.6 = x (√3 – 1)
∴ x = \(\frac{1.6}{\sqrt{3}-1}\)
∴ x = \(\frac{1.6}{\sqrt{3}-1} \times \frac{\sqrt{3}+1}{\sqrt{3}+1}\)
∴ x = \(\frac{1.6(\sqrt{3}+1)}{2}\)
∴ x = 0.8 (√3 + 1) મી
આમ, બેઠકની ઊંચાઈ 0.8(√3 + 1) મી છે.

પ્રશ્ન 9.
એક ટાવરના તળિયાથી એક ઇમારતની ટોચના ઉસેધકોણનું માપ 30° છે અને ઇમારતના તળિયાથી ટાવરની ટોચના ઉસેધકોણનું માપ 60° છે. જો ટાવરની ઊંચાઈ 50 મી હોય, તો ઈમારતની ઊંચાઈ શોધો.
ઉત્તરઃ
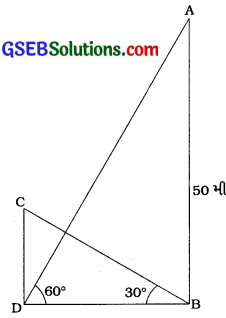
અહીં, AB ટાવર અને CD ઇમારત દર્શાવે છે.
આથી ∆ ABDમાં, ∠B = 90°; ∠D = 60° અને AB = 50 મી તથા ∆ CDBમાં, ∠D = 90° અને ∠B = 30°.
∆ ABDમાં, ∠B = 90°
∴ tan D = \(\frac{\mathrm{AB}}{\mathrm{BD}}\)
∴ tan 60° = \(\frac{50}{\mathrm{BD}}\)
∴ √3 = \(\frac{50}{\mathrm{BD}}\)
∴ BD = \(\frac{50}{\sqrt{3}}\) મી
વળી, ∆ CDBમાં, ∠D = 90°
∴ tan B = \(\frac{\mathrm{CD}}{\mathrm{BD}}\)
tan 30° = \(\frac{\text { CD }}{\left(\frac{50}{\sqrt{3}}\right)}\)
\(\frac{1}{\sqrt{3}}=\frac{C D}{\left(\frac{50}{\sqrt{3}}\right)}\)CD = \(\frac{50}{\sqrt{3}} \times \frac{1}{\sqrt{3}}\)
∴ CD = \(\frac{50}{3}\)
∴ CD = 16\(\frac{2}{3}\) મી
આમ, ઇમારતની ઊંચાઈ 16મી છે.

પ્રશ્ન 10.
એક 80 મી પહોળા માર્ગની બંને બાજુએ સમાન ઊંચાઈના બે સ્તંભ શિરોલંબ સ્થિતિમાં છે. માર્ગ પર વચ્ચે આવેલ કોઈ એક બિંદુએથી બંને સ્તંભની ટોચના ઉસેધકોણનાં માપ 60° અને 30° જણાય છે. તો દરેક સ્તંભની ઊંચાઈ શોધો તથા બંને સ્તંભનું નિરીક્ષણ બિંદુથી અંતર શોધો.
ઉત્તરઃ
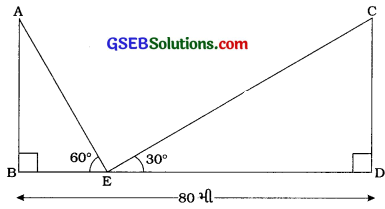
અહીં, AB અને CD સમાન ઊંચાઈના બે સ્તંભ દર્શાવે છે.
BD એ 80 મી પહોળો માર્ગ દર્શાવે છે તથા બિંદુ E એ માર્ગ પરનું નિરીક્ષણ સ્થાન દર્શાવે છે.
આથી ∆ ABEમાં, ∠B = 90° અને ∠E = 60°,
મ્યારે ∆ CDEમાં, ∠D = 90° અને ∠E = 30°.
વધુમાં, BD = માર્ગની પહોળાઈ = 80 મી.
ધારો કે, BE = x મી.
આથી DE = BD – BE = (80 – x) મી.
ધારો કે, AB = CD = h મી.
∆ ABEમાં, ∠B = 90°.
∴ tan E = \(\frac{\mathrm{AB}}{\mathrm{BE}}\)
∴ tan 60° = \(\frac{h}{x}\)
∴ √3 = \(\frac{h}{x}\)
x = \(\frac{h}{\sqrt{3}}\) મી ………….. (1)
∆ CDEમાં ∠D = 90°
tan E = \(\frac{C D}{D E}\)
tan 30° = \(\frac{h}{80-x}\)
\(\frac{1}{\sqrt{3}}=\frac{h}{80-x}\)80 – x = √3h
x = 80 – √3 h મી ………….(2)
(1) અને (2) પરથી,
\(\frac{h}{\sqrt{3}}\) = 80 – √3h
h = 80√3 – 3h
4h = 80√3
h = 20 /3 મી
હવે, x = \(\frac{h}{\sqrt{3}}\)
x = \(\frac{20 \sqrt{3}}{\sqrt{3}}\)
x = 20 મી
અને 80 – x = 80 – 20 = 60 મી આમ, દરેક સ્તંભની ઊંચાઈ 20/3 મી છે, નિરીક્ષણ સ્થાનનું નજીકના સ્તંભથી અંતર 20 મી છે તથા તેનું બીજા સ્તંભથી અંતર 60 મી છે.

પ્રશ્ન 11.
નહેરના એક કિનારા પર ટીવીનો ટાવર શિરોલંબ ઊભો કરવામાં આવેલ છે. ટાવરની સામેના બીજા કિનારા પર રહેલા એક બિંદુથી . ટાવરની ટોચનો ઉલ્લેધકોણ 60° છે. ટાવરના તળિયા અને નિરીક્ષણ બિંને જોડતી રેખા પર આવેલ અને નિરીક્ષણ બિંદુથી 20 મી દૂર બીજા એક બિંદુથી ટાવરની ટોચના ઉસેધકોણનું માપ 30° છે (જુઓ આકૃતિ), તો ટાવરની ઊંચાઈ અને નહેરની પહોળાઈ શોધો.
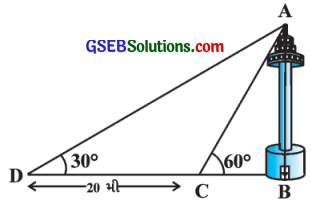
ઉત્તરઃ
અહીં, AB ટીવીનો ટાવર, BC એ નહેરની પહોળાઈ તથા C અને D એકબીજાથી 20 મી દૂર આવેલાં એવાં નિરીક્ષણ બિંદુઓ છે કે જેથી D, C અને B સમરખ થાય.
આથી ∆ ABCમાં, ∠B = 90° અને ∠C = 60° તથા ∆ ABDમાં, ∠B = 90° અને ∠D = 30° થાય, તેમજ CD = 20 મી થાય.
ધારો કે, ટાવરની ઊંચાઈ = AB = h મી અને નહેરની પહોળાઈ = BC = x મી.
આથી BD = BC + CD = (x + 20) મી થાય.
હવે, ∆ ABCમાં, ∠B = 90°
∴ tan C = \(\frac{\mathrm{AB}}{\mathrm{BC}}\)
tan 60° = \(\frac{h}{x}\)
√3 = \(\frac{h}{x}\) …………. (1)
x = \(\frac{h}{\sqrt{3}}\)
∆ ABDમાં, ∠B = 90° છે
tan D = \(\frac{\mathrm{AB}}{\mathrm{BD}}\)
tan 30° = \(\frac{h}{x+20}\)
\(\frac{1}{\sqrt{3}}=\frac{h}{x+20}\)x+ 20 = √3h
x = √3h – 20
(1) અને (2) પરથી,
\(\frac{h}{\sqrt{3}}\) = √3h – 20
h = 3h – 20√3
20√3 = 2h
h = 10√3 મી
હવે, x = \(\frac{h}{\sqrt{3}}\) = [(1) મુજબ]
x = \(\frac{10 \sqrt{3}}{\sqrt{3}}\)
∴ x = 10 મી
આમ, ટાવરની ઊંચાઈ 10√3 મી અને નહેરની પહોળાઈ 10 મી છે.

પ્રશ્ન 12.
7 મી ઊંચી ઇમારત પરથી એક કેબલ’ ટાવરની ટોચનો ઉલ્લેધકોણ 60° અને ટાવરના તળિયાનો અવસેધકોણ 45° છે, તો ટાવરની ઊંચાઈ શોધો.
ઉત્તરઃ
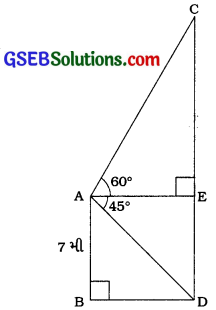
અહીં, AB એ 7 મી ઊંચી ઇમારત, CD એ ‘કેબલ’ ટાવર છે.
AE ⊥ CD દોરો, જેથી E એ CD પરનું બિંદુ હોય.
આથી ચતુષ્કોણ ∆ BDE લંબચોરસ આપેલ પરિસ્થિતિમાં ચોરસ) થાય.
હવે, AB = 7 મી; ∠E = 90°; ∠B = 90°; ∠CAE = 60° અને ∠EAD = 45°.
આથી ED = AB = 7 મી, ∠EAD = ∠ADB અને AE = BD.
∆ ABD, ∠B = 90°
tan D = \(\frac{\mathrm{AB}}{\mathrm{BD}}\)
tan 45 = \(\frac{7}{\mathrm{BD}}\)
1 = \(\frac{7}{\mathrm{BD}}\)
∴ BD = 7 મી
∴ AE = 7 મી
∆ CEAમાં, ∠E = 90°
tan A = \(\frac{\mathrm{CE}}{\mathrm{AE}}\)
tan 60° = \(\frac{\mathrm{CE}}{7}\)
√3 = \(\frac{\mathrm{CE}}{7}\)
CE = 7√3 મી
હવે, CD = CE + ED
= 7√3 + 7 = 7 (√3 + 1) મી
આમ, ટાવરની ઊંચાઈ 7(√3 + 1) મી છે.

પ્રશ્ન 13.
દરિયાની સપાટીથી 75 મી ઊંચી દીવાદાંડી પરથી અવલોકન કરતાં, દરિયામાં રહેલાં બે વહાણના અવસેધકોણનાં માપ 30° અને 45° માલૂમ પડે છે. જો એક વહાણ બીજાની બરાબર પાછળ હોય અને બંને વહાણ દીવાદાંડીની એક જ બાજુ પર આવેલ હોય, તો બંને વહાણ વચ્ચેનું અંતર શોધો.
ઉત્તરઃ
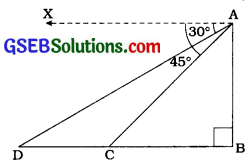
અહીં, AB એ દીવાદાંડી છે તથા C અને D એ દીવાદાંડીની એક જ તરફ રહેલા વહાણ છે.
આથી ∠B = 90°, AB = 75 મી, ∠XAD = 30° અને ∠XAC = 45°.
હવે, ∠ADB = ∠XAD = 30° અને ∠ACB = ∠XAC = 45° (યુગ્મકોણ)
∆ ABDમાં, ∠B = 90°
tanD = \(\frac{A B}{B D}\)
tan 30° = \(\frac{75}{\mathrm{BD}}\)
∴ \(\frac{1}{\sqrt{3}}=\frac{75}{\mathrm{BD}}\)
BD = 75√3 મી
∆ ABCમાં, ∠B = 90°
tan C = \(\frac{\mathrm{AB}}{\mathrm{BC}}\)
tan 45 = \(\frac{75}{\mathrm{BC}}\)
∴ 1 = \(\frac{75}{\mathrm{BC}}\)
∴ BC = 75 મી
હવે, બંને વહાણ વચ્ચેનું અંતર DC = BD – BC
= 75√3 – 75
= 75 (√3 – 1) મી
આમ, બંને વહાણ વચ્ચેનું અંતર 75(√3 – 1) મી છે.

પ્રશ્ન 14.
1.2 મી ઊંચાઈવાળી એક છોકરીને, જમીનથી 88.2 મી ઊંચાઈ પર રહેલું પવનને કારણે સમક્ષિતિજ રેખામાં ગતિ કરતું એક બલૂન જોવા મળે છે. કોઈ એક સમયે છોકરીને તેના ઉસેધકોણનું માપ 60° મળે છે. થોડા સમય બાદ બલૂનના ઉન્સેધકોણનું માપ 30° થાય છે (જુઓ આકૃતિ), તો આ સમય દરમિયાન બલૂને કાપેલું અંતર શોધો.
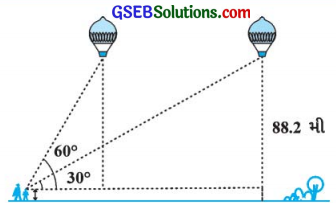
ઉત્તરઃ
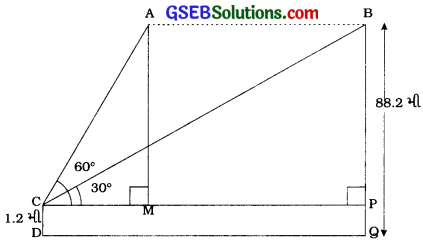
અહીં, A અને B એ બલૂનનાં બે સ્થાન છે.
CD એ 1.2 મી ઊંચાઈવાળી છોકરી છે.
DQ એ સમથળ જમીન છે અને CP એ છોકરીની આંખમાંથી પસાર થતી સમક્ષિતિજ રેખા છે.
AM ⊥ CP દોરો, જેથી M એ CPનું બિંદુ હોય.
આથી ∆ AMCમાં, ∠M = 90° અને ∠C = 60°;
∆ BPCમાં, ∠P = 90° અને ∠C = 30°;
PQ = CD = 1.2 મી, BQ = 88.2 મી અને તેથી
AM = BP = BQ – PQ
= 88.2 – 1.2 = 87 મી
∆ BPCમાં ∠P = 90°
tan C = \(\frac{\mathrm{BP}}{\mathrm{PC}}\).
tan 30° = \(\frac{87}{\mathrm{PC}}\)
\(\frac{1}{\sqrt{3}}=\frac{87}{\mathrm{PC}}\)
PC = 87√3 મી
∆ AMCમાં, ∠M = 90°
tan C = \(\frac{\mathrm{AM}}{\mathrm{MC}}\)
tan 60° = \(\frac{87}{\mathrm{MC}}\)
√3 = \(\frac{87}{\mathrm{MC}}\)
MC = \(\frac{87}{\sqrt{3}}\)
હવે, AB = MP (∵ AMPB લંબચોરસ છે.)
MP = PC – MC
= 87√3 – \(\frac{87}{\sqrt{3}}\)
= 87 (√3 – \(\frac{1}{\sqrt{3}}\))
= 87 \(\left(\frac{3-1}{\sqrt{3}}\right)\)
= 87 × \(\frac{2}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}\)
= 29 × 2 × √3
= 58√3 મી આથી AB = 58√3 મી
આમ, આપેલ સમય દરમિયાન બલૂને કાપેલું અંતર 583મી થાય.

પ્રશ્ન 15.
એક સુરેખ માર્ગ ટાવર તરફ જાય છે. ટાવરની ટોચ પર રહેલ એક વ્યક્તિ, ટાવર તરફ અચળ ઝડપથી આવતી એક મોટરકારના અવસેધકોણનું માપ 30° નોંધે છે. 6 સેકન્ડ પછી આ કારના અવસેધકોણનું માપ 60° થાય છે, તો કારને ટાવર સુધી પહોંચતાં કેટલો સમય લાગશે?
ઉત્તરઃ
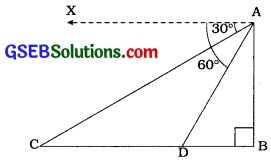
અહીં, AB એ ટાવર છે. C એ મોટરકારનું પ્રથમ સ્થાન છે અને D એ મોટરકારનું 6 સેકન્ડ પછીનું દ્વિતીય સ્થાન છે.
આથી AB = 90°, ∠XAC = 30° અને ∠XAD = 60°.
ધારો કે, AB = h મી.
હવે, ∠ACB = ∠XAC = 30° અને
∠ADB = ∠XAD = 60° (યુગ્મકોણ)
∆ ABCમાં, ∠B = 90°
cot C = \(\frac{B C}{A B}\)
cot 30° = \(\frac{\mathrm{BC}}{h}\)
√3 = \(\frac{\mathrm{BC}}{h}\)
BC = √3h મી
∆ ABDમાં, ∠B = 90°
cot D = \(\frac{\mathrm{BD}}{\mathrm{AB}}\)
cot 60° = \(\frac{\mathrm{BD}}{h}\)
\(\frac{1}{\sqrt{3}}=\frac{\mathrm{BD}}{h}\)BD = \(\frac{h}{\sqrt{3}}\) મી
મોટરકારે 6 સેકન્ડમાં કાપેલ અંતર = Cથી D સુધીનું અંતર
= CD
= BC – BD = √3h – \(\frac{h}{\sqrt{3}}\)
= \(\frac{3 h-h}{\sqrt{3}}\) = \(\frac{2 h}{\sqrt{3}}\) મી
મોટરકારને યવર સુધી પહોંચવા માટે બાકી રહેતું અંતર = BD = \(\frac{h}{\sqrt{3}}\) મી
\(\frac{2 h}{\sqrt{3}}\) મી અંતર (CD) કાપતાં લાગતો સમય = 6 સેકન્ડ
\(\frac{h}{\sqrt{3}}\) મી અંતર (BD) કાપતાં લાગતો સમય = 6 × \(\frac{h}{\sqrt{3}}\) × \(\frac{\sqrt{3}}{2 h}\) = 3 સેકન્ડ
આમ, મોટરકારને તેના દ્વિતીય સ્થાનથી ટાવર સુધી પહોંચતા ૩ સેકન્ડ લાગશે.

પ્રશ્ન 16.
ટાવરના તળિયામાંથી પસાર થતી રેખા પર તળિયાથી 4 મી અને 9 મી દૂર આવેલાં બે બિંદુથી ટાવરની ટોચના ઉર્સેધકોણનાં માપ કોટિકોણનાં માપ છે. સાબિત કરો કે, ટાવરની ઊંચાઈ 6 મી છે.
ઉત્તરઃ
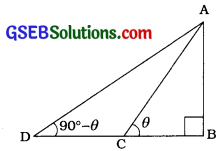
અહીં, AB ટાવર છે. C એ ટાવરના તળિયાથી 4 મી દૂર આવેલ નિરીક્ષણ બિંદુ છે અને D એ ટાવરના તળિયાથી 9 મી દૂર આવેલ નિરીક્ષણ બિંદુ છે.
આથી ∆ ABCમાં, ∠B = 90° અને BC = 4 મી તથા
∆ ABDમાં, ∠B = 90° અને BD = 9 મી.
ધારો કે, ∠ACB = θ
હવે, ∠ACB અને ∠ADB કોટિકોણ હોવાથી,
∠ADB = 90° – θ થાય.
∆ ABCમાં, ∠B = 90°
tan C = \(\frac{\mathrm{AB}}{\mathrm{BC}}\)
tan θ = \(\frac{\mathrm{AB}}{4}\)
∆ ABDમાં, ∠B = 90°
∴ tan D = \(\frac{\mathrm{AB}}{\mathrm{BD}}\)
∴ tan (90° – θ) = \(\frac{\mathrm{AB}}{9}\)
∴ cot θ = \(\frac{\mathrm{AB}}{9}\) [∵ tan (90° – θ) = cot θ] ……….. (2)
(1) અને (2)નો ગુણાકાર લેતાં,
tan θ cot θ = \(\frac{\mathrm{AB}}{4} \times \frac{\mathrm{AB}}{9}\)
∴ 1 = \(\frac{\mathrm{AB}^{2}}{36}\) (∵ tan θ cot θ = 1) .
∴ AB2 = 36 .
∴ AB = 6 (ટાવરની ઊંચાઈ કદી ઋણ ન હોય.) આમ, સાબિત થાય છે કે ટાવરની ઊંચાઈ 6 મી છે.