Gujarat Board GSEB Solutions Class 7 Maths Chapter 1 પૂર્ણાંક સંખ્યાઓ Ex 1.1 Textbook Exercise Questions and Answers.
Gujarat Board Textbook Solutions Class 7 Maths Chapter 1 પૂર્ણાંક સંખ્યાઓ Ex 1.1
1. આપેલ સંખ્યારેખા પર કોઈ એક દિવસનાં જુદાં જુદાં સ્થળોનાં તાપમાન ડિગ્રી સેલ્સિયસ (°C) વડે દર્શાવવામાં આવેલ છેઃ

(a) આ સંખ્યારેખાને જુઓ અને એના પર દર્શાવેલ સ્થળોનાં તાપમાન લખો.
(b) ઉપર આપેલ સ્થળોનાં તાપમાનમાં સૌથી ગરમ અને સૌથી ઠંડાં સ્થળોનાં તાપમાનમાં શું તફાવત છે?
(c) લાહૌલ સ્પિતિ અને શ્રીનગરના તાપમાનમાં શું તફાવત છે?
(d) શું આપણે કહી શકીએ કે શ્રીનગર અને શિમલાનું સંયુક્ત તાપમાન
શિમલાનાં તાપમાન કરતાં પણ ઓછું છે? શું તે શ્રીનગરના તાપમાન કરતાં પણ ઓછું છે?
ઉત્તરઃ
(a) સંખ્યારેખા ઉપર દર્શાવેલ સ્થળોનાં તાપમાન નીચે પ્રમાણે છે :
| સ્થળ | લાહોલ સ્પિતિ | શ્રીનગર | શિમલા | ઊટી | બેંગલૂરુ |
| તાપમાન | -8 °C | -2 °C | 5 °C | 14 °C | 22 °C |
(b) અહીં આપેલાં સ્થળોમાં સૌથી વધુ તાપમાન બેંગલુરુનું (22 °C) અને સૌથી ઓછું તાપમાન લાહોલ સ્થિતિનું -8°C) છે.
∴ આ બે સ્થળોનાં તાપમાનનો તફાવત = [22 – (-8)] °C
= (22 + 8) °C = 30 °C
(c) લાહોલ સ્થિતિનું તાપમાન (-8 °C) અને શ્રીનગરનું તાપમાન (-2 °C)
∴ આ બે સ્થળોનાં તાપમાનનો તફાવત = [(-2) – (-8)] °C
[: (-2) – (8)] = (-2 + 8)° C = 6°C
(d) શ્રીનગર અને શિમલાનાં તાપમાનનો સરવાળો = (-2 + 5) °C
= ૩°C
હવે, શિમલાનું તાપમાન 5°C છે. જુઓ 3 °C < 5 °C
હા, શ્રીનગર અને શિમલાના તાપમાનનો સરવાળો એ શિમલાના તાપમાન કરતાં ઓછો છે.
શ્રીનગરનું તાપમાન (-2 °C) છે. જ્યાં 3°C > (-2°C)
ના, શ્રીનગર અને શિમલાના તાપમાનનો સરવાળો એ શ્રીનગરના તાપમાન કરતાં ઓછો નથી.
![]()
2. કોઈ એક પ્રશ્નોત્તરીમાં સાચા જવાબ માટે ધન અંક આપવામાં આવે છે અને ખોટા જવાબ માટે ત્રણ અંક આપવામાં આવે છે. જો પાંચ ક્રમિક રાઉન્ડમાં જૈકે પ્રાપ્ત કરેલ અંકો (ગુણ) 25, -5, -10, 15 અને 10 છે, તો અંતમાં તેના કુલ ગુણ કેટલા થશે?
ઉત્તરઃ
પહેલા રાઉન્ડમાં મળેલા અંક = 25
બીજા રાઉન્ડમાં મળેલા અંક = – 5
ત્રીજા રાઉન્ડમાં મળેલા અંક = – 10
ચોથા રાઉન્ડમાં મળેલા અંક = 15
પાંચમા રાઉન્ડમાં મળેલા અંક = 10
∴ પાંચેય રાઉન્ડમાં મળેલા કુલ અંક = 25 + (-5) + (-10) + 15 + 10
= 25 + 15 + 10 + (-5) + (-10)
= 50 – 15 = 35
આમ, પાંચ રાઉન્ડમાં મેળવેલા કુલ અંક (ગુણ) 35 થશે.
3. સોમવારે શ્રીનગરનું તાપમાન -5 °C હતું અને મંગળવારનું તાપમાન 2 °C ઓછું થયું, તો મંગળવારે શ્રીનગરનું તાપમાન શું હતું? બુધવારે તાપમાન 4 °C વધી ગયું, તો આ દિવસે તાપમાન કેટલું હતું?
ઉત્તરઃ
સોમવારે શ્રીનગરનું તાપમાન = -5 °C
હવે, મંગળવારે તાપમાન 2°C ઓછું થયું છે.
∴ મંગળવારે શ્રીનગરનું તાપમાન = [(-5) + (-2)] °C = -7 °C … (1)
હવે, બુધવારે તાપમાન 4 °C વધી ગયું છે.
∴ બુધવારનું તાપમાન = [(-7) + 4] °C = -3°C… (2)
આમ, મંગળવારનું તાપમાન -7 °C અને
બુધવારનું તાપમાન -3 °c હોય.
![]()
4. એક વિમાન સમુદ્રતટથી 5000 મીટરની ઊંચાઈએ ઊડે છે. કોઈ એક ચોક્કસ બિંદુ પર આ વિમાન સમુદ્રની સપાટીથી 1200 મીટર નીચે તરતી સબમરીનની બરાબર ઉપર છે. સબમરીન અને વિમાન વચ્ચેનું લંબઅંતર શું થશે?
ઉત્તરઃ
સમુદ્રતટની ઊંચાઈ 0 મીટર છે અને વિમાન તેનાથી 5000 મીટર ઊંચાઈએ ઊડે છે.
∴ વિમાન અને દરિયાની સપાટી વચ્ચેના અંતરનો તફાવત = 5000 મીટર હવે, સમુદ્રની સપાટીથી 1200 મીટર નીચે સબમરીન છે. જે વિમાનની બરાબર નીચે છે.
∴ દરિયાની સપાટીથી સબમરીનના અંતરનો તફાવત = 1200 મીટર
હવે, વિમાન અને સબમરીન વચ્ચેનું લંબઅંતર = વિમાનથી દરિયાની સપાટીનું અંતર + દરિયાની સપાટીથી સબમરીનનું અંતર
= 5000 મી + 1200 મી
= 6200 મી
∴ સબમરીન અને વિમાન વચ્ચે 6200 મીટરનું અંતર થશે.
5. મોહન તેના બૅન્કના ખાતામાં ₹ 2000 જમા કરાવે છે અને બીજે દિવસે તેમાંથી ₹ 1642 ઉપાડે છે. જો ઉપાડેલ રકમને ઋણ પૂર્ણાક વડે દર્શાવાય, તો જમા કરાવેલ રકમને તમે કઈ રીતે દર્શાવશો? ઉપાડ પછી મોહનના ખાતામાં કેટલી સિલક છે તે શોધો.
ઉત્તરઃ
બૅન્કમાં જમા કરાવાતી રકમને ધન પૂર્ણાકમાં અને ઉપાડાતી રકમને ત્રણ પૂર્ણાકમાં દર્શાવાય છે.
મોહને જમા કરાવેલી રકમ = + ₹ 2000
મોહને ઉપાડેલી રકમ = – ₹ 1642
મોહનના ખાતામાં સિલક = ₹ (2000 – 1642) = ₹ 358
:. મોહનના ખાતાની સિલક ₹ 358 છે.
6. રીટા બિંદુ Aથી પૂર્વ દિશા તરફ બિંદુ B સુધી 20 કિલોમીટરનું અંતર કાપે છે. એ જ રસ્તે તે બિંદુ Bથી પશ્ચિમ દિશા તરફ 30 કિલોમીટરનું અંતર કાપે છે. જો પૂર્વ તરફ કાપેલ અંતરને ધન પૂર્ણાક દર્શાવવામાં આવે, તો પશ્ચિમ દિશા તરફ કાપેલ અંતરને તમે કેવી રીતે દર્શાવશો? બિંદુ નથી તેની અંતિમ સ્થિતિને તમે કઈ પૂર્ણાંક સંખ્યા વડે દર્શાવશો?

ઉત્તરઃ
પૂર્વ દિશા અને પશ્ચિમ દિશા પરસ્પર વિરોધી દિશાઓ છે.

જો પૂર્વ દિશામાં ચાલવાના અંતરને ધન પૂર્ણાક ગણીએ, તો પશ્ચિમ દિશામાં પાછા ફરવાનું અંતર ઋણ પૂર્ણાક ગણાય.
રીટા A બિંદુથી પૂર્વ દિશામાં થી B સુધી ચાલી એટલે કે + 20 કિમી ચાલી. હવે, રીટા B બિંદુથી પશ્ચિમ દિશામાં C બિંદુ સુધી ચાલી એટલે કે – 30 કિમી ચાલી.
આમ, રીટાનું અંતિમ સ્થાન (પશ્ચિમમાં) = [+ 20 + (-30)] કિમી
= (- 10) કિમી
∴ રીટા અંતે A બિંદુથી પશ્ચિમમાં (-10) કિમી બિંદુએ હોય.
![]()
7. એક જાદુઈ ચોરસમાં દરેક હરોળ, કૉલમ અને વિકર્ણ સમાન સરવાળો ધરાવે છે. આપેલ ચોરસમાં કયો જાદુઈ ચોરસ છે તે તપાસો:
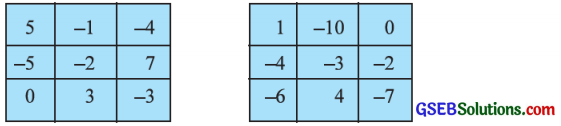
ઉત્તરઃ
ચોરસ (i):
પહેલી હરોળનો સરવાળો = 5 + (-1) + (-4) = 5 + (-5) = 0
બીજી હરોળનો સરવાળો = (-5) + (-2) + 7 = -7 + 7 = 0
ત્રીજી હરોળનો સરવાળો = 0 + 3 + (-3) = 3 + (-3) = 0
પહેલા કૉલમનો સરવાળો = 5 + (-5) + 0 = 5 + (-5) = 0
બીજા કૉલમનો સરવાળો = (-1) + (-2) + 3 = (-3) + 3 = 0
ત્રીજા કૉલમનો સરવાળો = (-4) + 7 + (-3) = (-7) + 7 = 0
એક વિકર્ણની દિશાએ સરવાળો = 5 + (-2) + (-3) = 5 – 5 = 0
બીજા વિકર્ણની દિશાએ સરવાળો = 0 + (-2) + (-4) = 0 + (-6) = -6
અહીં, – 6 ≠ 0 (જુઓ : ઉપરના બધા સરવાળા 0 છે.).
∴ ચોરસ (i) એ જાદુઈ ચોરસ નથી.
ચોરસ (ii):
પહેલી હરોળનો સરવાળો = 1 + (-10) + 0 = 1 – 10 = – 9
બીજી હરોળનો સરવાળો = (-4) + (-3) + (-2) = (-7) + (-2) = -9
પૂર્ણાંક સંખ્યાઓ ત્રીજી હરોળનો સરવાળો = (-6) + 4 + (-7) = (-13) + 4 = – 9
પહેલા કૉલમનો સરવાળો = 1 + (-4) + (-6) = 1 + (-10) = – 9
બીજા કૉલમનો સરવાળો = (-10) + (-3) + 4 = (-13) + 4 = – 9
ત્રીજા કૉલમનો સરવાળો = 0 + (-2) + (-7) = 0 + (-9) = – 9
એક વિકર્ણની દિશાએ સરવાળો = 1 + (-3) + (-7) = 1 + (-10) = – 9
બીજા વિકર્ણની દિશાએ સરવાળો = (-6) + (-3) + 0 = (-9) + 0 = -9
અહીં, દરેક હરોળ, દરેક કૉલમ અને દરેક વિકર્ણની દિશાએ સરવાળો સરખો (-9) મળે છે.
∴ ચોરસ (ii) એ જાદુઈ ચોરસ છે.
8. નીચે આપેલી કિંમતો વ અને b માટે a – (-b) = a + ચકાસો.
(i) a = 21, b = 18
ઉત્તરઃ
અહીં, a = 21 અને b = 18
ડો.બા. = a – (-b)
= 21 – (-18) = 21 + 18 = 39
જ.બા. = a + b
= 21 + 18 = 39
∴ ડા.બા. = જ.બા.
∴ a – (- b) = a + b સાચું છે.
(ii) a = 118, b = 125
ઉત્તરઃ
અહીં, a = 118 અને b = 125
ડા.બા. = a – (- b)
= 118 – (- 125) = 118 + 125 = 243
જ.બા. = a + b
= 118 + 125 = 243
∴ ડા.બા. = જ.બા.
∴ a – (- b) = a + b સાચું છે.
(iii) a = 75, b = 84
ઉત્તરઃ
અહીં, a = 75 અને b = 84
ડા.બો. = a – (- b)
= 75 – (- 84) = 75 + 84 = 159
જ.બા. = a + b
= 75 + 84 = 159
∴ ડા.બા. = જ.બા.
∴ a – (-b) = a + b સાચું છે.
(iv) a = 28, b = 11
ઉત્તરઃ
અહીં, a = 28 અને b = 11
ડો.બા. = a – (- b)
= 28 – (-11) = 28 + 11 = 39
જ.બા. = a + b
= 28 + 11 = 39
ડા.બા. = જ.બા.
∴ a – (-b) = a + b સાચું છે.
![]()
9. વાક્યને સાચું બનાવવા માટે ખાનામાં >, < અથવા = ચિહ્નનો ઉપયોગ કરોઃ
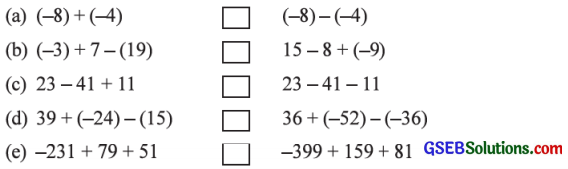
ઉત્તરઃ
(a) ડો.બા. = (-8) + (-4) = – 8 – 4 = – 12
જ.બા. = (-8) – (-4) = – 8 + 4 = – 4
હવે, (- 12) < (4)
![]()
(b) ડો.બા. = (-1) + 7 – (19) = – 3 + 7 – 19 = – 3 – 19 + 7
= – 22 + 7 = – 15
જ.બા. = 15 – 8 + (-9) = 15 + (- 8 – 9)
= 15 + (-17) = -2
હવે, (-15) – (-2)
![]()
(c) ડો.બા. = 23 – 41 + 11 = 23 + 11 – 41 = 34 – 41 = -7
જ.બા. = 23 – 41 – 11 = 23 – 2 = -29
હવે, (-7) > (-29)
![]()
(d) ડો.બા. == 39 + (-24) – (15) = 39 + (-39) = 0
જ.બા. = 36 + (- 52) – – 36) = 36 + (- 52) + 36
= 72 + (- 52) = 20
હવે, 0 < 20
![]()
(e) ડા.બા. = (-231) + 79 + 51 = – 231 + 130 = – 101
જ.બા. = (-399) + 159 + 81 = -399 + 240 = – 159
હવે, (-101) > (-159)
![]()
![]()
10. પાણીની ટાંકીની અંદર પગથિયાં આવેલાં છે. એક વાંદરો સૌથી ઉપરના પગથિયા પર બેઠો છે (અર્થાત્ સૌથી પહેલું પગથિયું). પાણીનું સ્તર નવમા પગથિયા પર છે ?
(i) તે એક કૂદકામાં ત્રણ પગથિયાં નીચે અને પછીના કૂદકામાં 2 પગથિયાં ઉપર આવે છે, તો તે કેટલામાં કૂદકે પાણીના સ્તરે પહોંચશે?
(ii) પાણી પી લીધા પછી તે પાછો ફરે છે. આ માટે તે 4 પગથિયાં ઉપર કૂદકો મારે છે અને તે પછી દરેક ચાલમાં 2 પગથિયાં નીચે કૂદંકો મારે છે, તો તે કેટલામાં કૂદકે ટોચના પગથિયે પાછો પહોંચશે?
(iii) નીચેની તરફનાં પગથિયાંની સંખ્યાને ઋણ પૂર્ણાક દર્શાવીએ અને ઉપરની તરફનાં પગથિયાંની સંખ્યાને ધન પૂર્ણાક દર્શાવીએ. તેની ચાલને દર્શાવવા માટે ભાગ (i) અને (ii) દ્વારા નીચેની બાબતો પૂર્ણ કરો:
(a) -3 + 2 – …….. = – 8
(b) 4 – 2 + ……… = 8.
જેમાં (૧) રકમ (-8) એ આઠ પગથિયાં નીચે જવાનું દર્શાવે છે,
તો (b)માં રકમ 8 શું દર્શાવે છે?
ઉત્તરઃ
(i) વાંદરો પહેલા પગથિયે (સૌથી ઊંચા પગથિયે) બેઠો છે.
પગથિયું
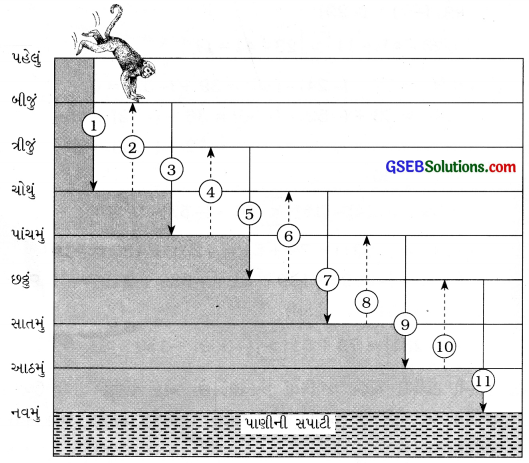
કૂદકા મારતો વાંદરો …
– પહેલ કૂદકે ચોથા પગથિયે હોય.
– બીજે કૂદકે બીજા પગથિયે હોય.
– ત્રીજે કૂદકે પાંચમા પગથિયે હોય.
– ચોથે કૂદકે ત્રીજા પગથિયે હોય.
– પાંચમે કૂદકે છઠ્ઠા પગથિયે હોય.
– છà કૂદકે ચોથા પગથિયે હોય.
– સાતમે કૂદકે સાતમા પગથિયે હોય.
– આઠમે કૂદકે પાંચમા પગથિયે હોય.
– નવમે કૂદકે આઠમા પગથિયે હોય.
– દસમે કૂદકે છઠ્ઠા પગથિયે હોય.
– અગિયારમા કૂદકે નવમા પગથિયે હોય જે પાણીની સપાટી છે.
આમ, વાંદરા માટે પાણીની સપાટી પાસે જવા જરૂરી કૂદકા = 11
(ii) હવે વાંદરો પાણીની સપાટી પાસે નવમા પગથિયે છે.
પગથિયું
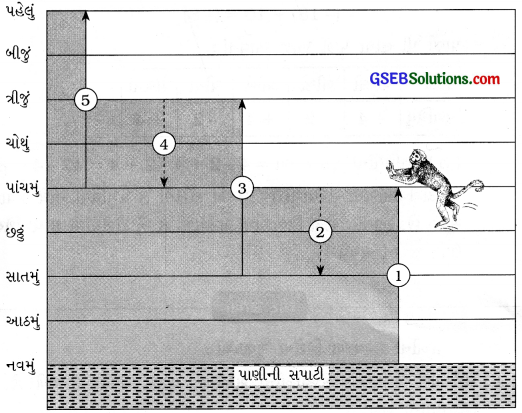
કૂદકા મારતો વાંદરો…
– પહેલ કૂદકે પાંચમા પગથિયે હોય.
– બીજે કૂદકે સાતમા પગથિયે હોય.
– ત્રીજે કૂદકે ત્રીજા પગથિયે હોય.
– ચોથે કૂદકે પાંચમા પગથિયે હોય.
– પાંચમા કૂદકે પહેલે પગથિયે હોય.
આમ, વાંદરા માટે ઉપર આવવા જરૂરી કૂદકા = 5
(iii) વાંદરો ઉપર તરફ કૂદકા મારે તેને ધન પૂર્ણાકમાં અને પાણી તરફ કૂદકા મારે તેને ત્રણ પૂર્ણાકમાં દર્શાવીએ તો –
પાણી પીવા જતાં :

(a) પગથિયાંની કુલ સંખ્યા
= – 3 + 2 – 3 + 2 – 3 + 2 – 3 + 2 – 3 + 2 – 3
= (-18) + 10 = (-8)
પાણી પી લીધા પછી પાછા આવતાં :
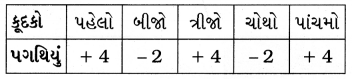
(b) પગથિયાંની કુલ સંખ્યા = 4 – 2 + 4 – 2 + 4 = 12 – 4 = 8
પહેલા વિભાગમાં સરવાળો (-8) એ ટાંકીમાં 8 પગથિયાં નીચે જવાનું સૂચવે છે. આથી, બીજા વિભાગમાં સરવાળો 8 એ ટાંકીમાંથી 8 પગથિયાં ઉપર જવાનું સૂચવે છે.