Gujarat Board GSEB Solutions Class 7 Maths Chapter 3 માહિતીનું નિયમન InText Questions and Answers.
Gujarat Board Textbook Solutions Class 7 Maths Chapter 3 માહિતીનું નિયમન InText Questions
પ્રયત્ન કરો : (પાઠ્યપુસ્તક પાન નંબર 59)
તમારી શાળાના ઓછામાં ઓછા 20 વિદ્યાર્થીઓ(છોકરાઓ અને છોકરીઓ)નું વજન (કિલોગ્રામમાં) કરો. મળેલી માહિતીને ગોક્વો અને નીચે આપેલા પ્રશ્નોના જવાબ માહિતીને આધારે આપો:
(i) બધામાં સૌથી વધુ વજન કોનું છે?
(ii) સૌથી વધુ વખત આવતું હોય તેવું વજન કર્યું?
(iii) તમારા અને તમારા ખાસ મિત્રના વજનમાં શું તફાવત છે?
ઉત્તરઃ
ધારો કે મારા વર્ગના 20 વિદ્યાર્થીઓનાં વજન કિગ્રામાં નીચે પ્રમાણે છે :
36 34 39 33 34 36 37 38 33 32 35 36 38 33 36 35 37 38 39 40
વિદ્યાર્થીઓનાં વજન ઊતરતા ક્રમમાં ગોઠવતાં :
40 39 39 38 38 37 37 36 36 36 36 36 35 35 34 34 33 33 33 32
(i) વર્ગમાં સૌથી વધુ વજનનો એક વિદ્યાર્થી અજય છે. તેનું વજન 40 કિગ્રા છે.
(ii) સૌથી વધુ વખત આવતું હોય તેવું વજન 36 કિગ્રા છે. આવા 5 વિદ્યાર્થી છે.
(iii) મારું વજન 37 કિગ્રા છે. મારા ખાસ મિત્ર વિમલનું વજન 39 કિગ્રા છે.
અમારા બંનેના વજનનો તફાવત = 39 કિગ્રા – 37 કિગ્રા = 2 કિગ્રા છે.
પ્રયત્ન કરો : (પાઠ્યપુસ્તક પાન નંબર 61)
આખા અઠવાડિયા દરમિયાન તમારા ભણવાના કલાકની સરાસરી તમે કેવી રીતે શોધી શકશો?
ઉત્તરઃ
અઠવાડિયાના સાત દિવસનું મારું ભણવાનું સમયપત્રક નીચે પ્રમાણે છે :

અક્વાડિયામાં ભણવાનો કુલ સમય = (2 + 5 + 4 + 5 + 6 + 6 + 7) કલાક
= 35 કલાક
હવે, અઠવાડિયાના 7 દિવસનું આ સમયપત્રક છે.
![]()
કુલ દિવસો આમ, સરેરાશ ભણવાના 5 કલાક છે.
![]()
વિચારો, ચર્ચા કરો અને લખો : (પાઠ્યપુસ્તક પાન નંબર 61)
શું સરાસરી દરેક અવલોકનથી મોટી છે?
ઉત્તરઃ
ના, સરાસરી એ દરેક અવલોકન કરતાં મોટી ન જ હોય.
કારણઃ સરાસરી એ અમુક જ અવલોકનથી મોટી હોય. (અમુક અવલોકનથી નાની પણ હોઈ શકે.)
શું સરાસરી દરેક અવલોકનથી નાની છે?
ઉત્તરઃ
ના, સરાસરી એ દરેક અવલોકનથી નાની ન જ હોય.
કારણ: સરાસરી એ અમુક અવલોકનથી મોટી અને અમુક અવલોકનથી નાની હોય.
પ્રયત્ન કરો : (પાઠ્યપુસ્તક પાન નંબર 61)
1. એક અઠવાડિયા દરમિયાનના તમારા ઊંઘવાના કલાકની સરાસરી શોધો.
ઉત્તરઃ
1. મારા અઠવાડિયામાં ઊંઘવાના કલાકો નીચે પ્રમાણે છે :
સોમવાર : 7 કલાક
મંગળવાર : 8 કલાક
બુધવાર : 10 કલાક
ગુરુવાર : 7 કલાક
શુક્રવાર : 9 કલાક
શનિવાર : 8 કલાક
રવિવાર : 7 કલાક
અઠવાડિયામાં ઊંઘવાનો કુલ સમય = (7 + 8 + 10 + 7 + 9 + 8 + 7) કલાક
= 56 કલાક
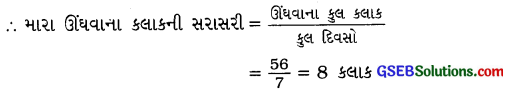
આમ, ઊંઘવાના કલાકની સરાસરી 8 કલાક છે.
2. \(\frac {1}{2}\) અને \(\frac {1}{3}\) વચ્ચેની ઓછામાં ઓછી 5 સંખ્યા શોધો.
ઉત્તરઃ
\(\frac {1}{2}\) અને \(\frac {1}{3}\) વચ્ચેની ઓછામાં ઓછી 5 સંખ્યા નીચે મુજબ છેઃ
\(\frac {1}{2}\) અને \(\frac {1}{3}\) વચ્ચેની સંખ્યા : વચ્ચેની સંખ્યા શોધવા બે અપૂર્ણાંકોના સરવાળાને 2 વડે ભાગવા પડે.

![]()
પ્રયત્ન કરો : (પાઠ્યપુસ્તક પાન નંબર 65)
નીચેનાનો બહુલક શોધોઃ
(i) 2, 6, 5, 3, 0, 3, 4, 8, 2, 4, 5, 2, 4
(ii) 2, 14, 16, 12, 14, 14, 16, 14, 10, 14, 18, 14
ઉત્તરઃ
(i) આપેલ પ્રાપ્તાંકો : 2, 6, 5, 3, 0, 3, 4, 3, 2, 4, 5, 2, 4
આ પ્રાપ્તાંકો ચડતા ક્રમમાં
0, 2, 2, 2, 3, 3, 3, 4, 4, 4, 5, 5, 6
જુઓ અહીં પ્રાપ્તાંકો 2, 3 અને 4 એ સૌથી વધુ વખત (ત્રણ-ત્રણ વખત) છે.
∴ આપેલ પ્રાપ્તાંકોનો બહુલક 2, 3 અને 4 છે.
(ii) આપેલ પ્રાપ્તાંકો 2, 14, 16, 12, 14, 14, 16, 14, 10, 14, 18, 14
આ પ્રાપ્તાંકો ચડતા ક્રમમાં :
2, 10, 12, 14, 14, 14, 14, 14, 14, 16, 16, 18
જુઓ અહીં પ્રાપ્તાંક 14 એ સૌથી વધુ વખત (6 વખત) છે.
∴ આપેલ પ્રાપ્તાંકોનો બહુલક 14 છે.
વિચારો, ચર્ચા કરો અને લખો : (પાઠ્યપુસ્તક પાન નંબર 65)
શું આપેલ માહિતીસમૂહને એક કરતાં વધુ બહુલક હોઈ શકે?
ઉત્તરઃ
હા, આપેલ માહિતીસમૂહને એક કરતાં વધુ બહુલક હોઈ શકે.
![]()
આ કરો : (પાઠ્યપુસ્તક પાન નંબર 65)
1. તમારા વર્ગના વિદ્યાર્થીઓની ઉંમર વર્ષમાં લખો. તેને કોષ્ટકમાં ગોઠવી બહુલક શોધો.
ઉત્તરઃ
મારા વર્ગના 20 વિદ્યાર્થીઓની ઉંમર (વર્ષમાં) આ પ્રમાણે છે :
| રોલ નંબર | ઉંમર (વર્ષમાં) |
| 1 | 12 |
| 2 | 13 |
| 3 | 14 |
| 4 | 14 |
| 5 | 13 |
| 6 | 12 |
| 7 | 13 |
| 8 | 13 |
| 9 | 12 |
| 10 | 12 |
| 11 | 14 |
| 12 | 14 |
| 13 | 13 |
| 14 | 14 |
| 15 | 12 |
| 16 | 13 |
| 17 | 12 |
| 18 | 13 |
| 19 | 12 |
| 20 | 13 |
આ માહિતીનો બહુલક 13 છે.
2. તમારા સહાધ્યાયીઓની ઊંચાઈ સેન્ટિમીટરમાં માપો અને તેનો બહુલક શોધો.
ઉત્તરઃ
મારા વર્ગના 20 વિદ્યાર્થીઓની ઊંચાઈ (સેમીમાં) આ પ્રમાણે છે:
| રોલ નંબર | ઊંચાઈ (સેમીમાં) |
| 1 | 116 |
| 2 | 115 |
| 3 | 114 |
| 4 | 116 |
| 5 | 114 |
| 6 | 116 |
| 7 | 117 |
| 8 | 114 |
| 9 | 118 |
| 10 | 116 |
| 11 | 116 |
| 12 | 117 |
| 13 | 114 |
| 14 | 116 |
| 15 | 115 |
| 16 | 118 |
| 17 | 120 |
| 18 | 116 |
| 19 | 119 |
| 20 | 116 |
આ માહિતીનો બહુલક 116 છે.
![]()
પ્રયત્ન કરો: (પાઠ્યપુસ્તક પાન નંબર 65 – 66)
1. નીચેની માહિતીનો બહુલક શોધોઃ
12, 14, 12, 16, 15, 13, 14, 18, 19, 12, 14, 15, 16, 15, 16, 16, 18, 17, 13, 16, 16, 18, 15, 13, 15, 17, 13, 14, 15, 13, 15, 14
ઉત્તરઃ
આ માહિતીને આવૃત્તિ કોષ્ટકમાં ગોઠવીશું:
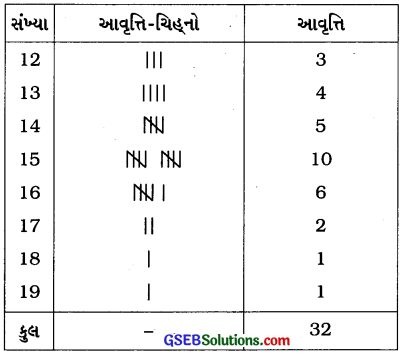
અહીં માહિતીમાં સંખ્યા 15ની સૌથી વધુ આવૃત્તિ છે. (જુઓઃ 10 આવૃત્તિ છે.)
∴ માહિતીનો બહુલક 15 છે.
2. નીચે 25 બાળકોની ઊંચાઈ (સેમીમાં) આપેલ છેઃ
168, 165, 163, 160, 163, 161, 162, 164, 163, 162, 164, 163, 100, 163, 160, 165, 163, 162, 163, 164, 163, 160, 165, 163, 162
તેમની ઊંચાઈનો બહુલક કેટલો હશે? અહીંયા બહુલકથી આપણે શું સમજીએ છીએ?
ઉત્તરઃ
આ માહિતીને આવૃત્તિ કોષ્ટકમાં ગોઠવીએ :
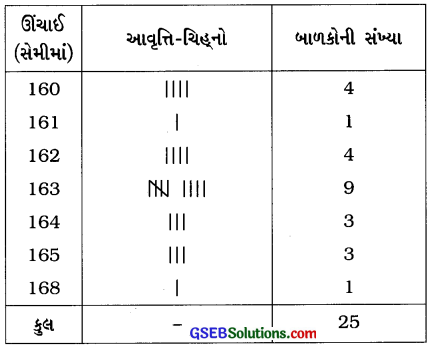
અહીં ઊંચાઈ 163 સેમીની આવૃત્તિ સૌથી વધુ છે. (જુઓઃ 9 આવૃત્તિ છે.)
∴ માહિતીનો બહુલક 163 સેમી છે.
અહીં બહુલક એ બાળકોની ઊંચાઈની સરાસરી દર્શાવે છે. સમજી શકાય કે ઘણાખરાં વિદ્યાર્થીઓની ઊંચાઈ 163 સેમી છે.
![]()
પ્રયત્ન કરો: (પાઠ્યપુસ્તક પાન નંબર 66)
તમારા મિત્રો સાથે ચર્ચા કરો અને જવાબ આપોઃ
(a) એવી બે સ્થિતિ આપો કે જ્યાં સરાસરીનો યોગ્ય પ્રતિનિધિ મૂલ્યના સ્વરૂપે ઉપયોગ થતો હોય.
(b) એવી બે સ્થિતિ આપો કે જેમાં બહુલકના મૂલ્યનો યોગ્ય પ્રતિનિધિ મૂલ્યના સ્વરૂપે ઉપયોગ થતો હોય.
ઉત્તરઃ
(a) (i) ક્રિકેટના ખેલાડીઓએ જુદી જુદી રમતોમાં કરેલા રન
(ii) વિદ્યાર્થીઓએ જુદી જુદી પરીક્ષામાં મેળવેલા ગુણ
(b) (i) એક જ વર્ગના વિદ્યાર્થીઓએ પહેરેલા પગના બૂટની સાઇઝ
(ii) દુકાનદારનું વર્ષ દરમિયાન ચોક્કસ માપનાં ટી-શર્ટનું વેચાણ
પ્રયત્ન કરો : (પાઠ્યપુસ્તક પાન નંબર 67)
તમારા મિત્ર આપેલ માહિતીનો મધ્યસ્થ અને બહુલક શોધે છે. તમારા મિત્રની કોઈ ભૂલ થઈ હોય, તો દર્શાવો અને સુધારોઃ
35, 32, 35, 42, 38, 32, 34
મધ્યસ્થ = 42, બહુલક = 32
ઉત્તરઃ
આપેલી માહિતી : 35, 32, 35, 42, 38, 32, 34
આ માહિતી ચડતા ક્રમમાં : 32, 32, 34, 35, 35, 38, 42
(i) માહિતીમાં બરાબર વચ્ચેનો પ્રાપ્તાંક 35 છે.
∴ આ માહિતીનો મધ્યસ્થ = 35
∴ માહિતીનો સાચો મધ્યસ્થ 35 છે.
(ii) માહિતીમાં 32 બે વખત અને 35 બે વખત છે. જે સૌથી વધુ વખત છે.
∴ માહિતીનો બહુલક 32 અને 35 છે.
∴ માહિતીનો સાચો બહુલક 32 અને 35 બને છે.
![]()
પ્રયત્ન કરો (પાઠ્યપુસ્તક પાન નંબર 71-72)
1. આપવામાં આવેલ લંબ આલેખ જુદી જુદી કંપનીઓ દ્વારા બનાવવામાં આવેલ પાણી અવરોધક ઘડિયાળની તપાસ માટે કરવામાં આવેલા એક સર્વેક્ષણનો છે.
તેમાંની દરેક કંપનીનો દાવો હતો કે તેમની ઘડિયાળ પાણી અવરોધક છે.
તપાસ કર્યા પછી મેળવેલ આ પરિણામ છે?
(a) શું તમે દરેક કંપની માટે લીક થતી હોય તેવી ઘડિયાળ અને કુલ ઘડિયાળની સંખ્યાને અપૂર્ણાંક સ્વરૂપમાં દર્શાવી શકશો?
(b) આ પરથી તમે કહી શકશો કે કઈ કંપનીની ઘડિયાળ વધુ સારી છે?
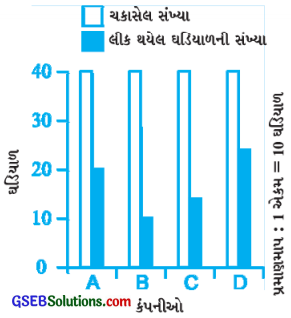
ઉત્તરઃ
(a) આપેલા દ્વિ-લંબ આલેખ પરથી જણાય છે કે –
દરેક કંપનીની તપાસમાં લીધેલી ઘડિયાળ = 40
દરેક કંપનીની લીક થતી હોય તેવી ઘડિયાળ અને કુલ ઘડિયાળનો ગુણોત્તર શોધીએ.

(b) ઉપરના ગુણોત્તરમાં સૌથી નાનો અપૂર્ણાંક B કંપનીનો છે જે સૂચવે છે કે
તેની ઘડિયાળો ઓછી લીક થઈ છે.
[∵ \(\frac{1}{4}<\frac{3}{8}<\frac{1}{2}<\frac{5}{8}\)]
∴ કંપની Bની ઘડિયાળ વધુ સારી છે.
2. નીચે 1995, 1996, 1997 અને 1998માં વેચાયેલ અંગ્રેજી અને હિન્દી વિષયની ચોપડીઓની સંખ્યા દર્શાવેલ છે :
| વર્ષ | 1995 | 1996 | 1997 | 1998 |
| અગ્રેજી | 350 | 400 | 450 | 620 |
| હિન્દી | 500 | 525 | 600 | 650 |
દ્વિ-લંબ આલેખ દોરી નીચેના પ્રશ્નોના જવાબ આપોઃ
(a) ક્યા વર્ષમાં બંને ભાષાનાં પુસ્તકોના વેચાણ વચ્ચેનો તફાવત સૌથી ઓછો હતો?
(b) શું તમે કહી શકશો કે અંગ્રેજી વિષયના પુસ્તકની માંગ ઝડપથી વધી છે?
કારણ આપો.
ઉત્તરઃ
આપેલ માહિતી પરથી દ્વિ-લંબ આલેખ નીચે પ્રમાણે તૈયાર થાય :
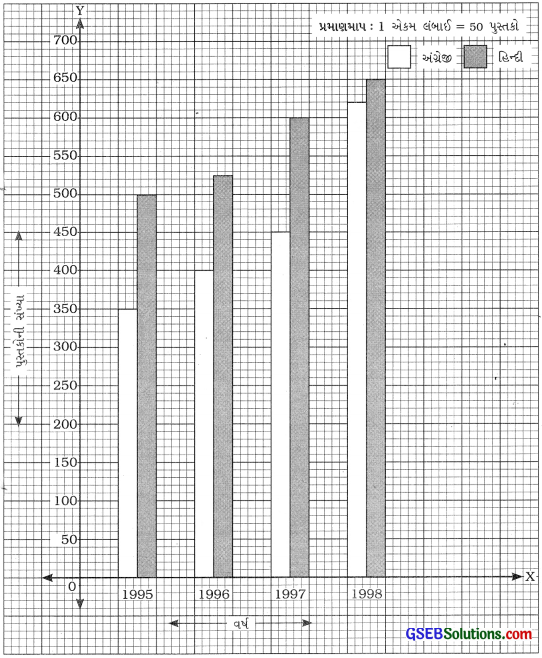
(a) અંગ્રેજી અને હિન્દી ભાષાનાં પુસ્તકોના વેચાણનો તફાવત :
1995 વર્ષમાં : 500 – 350 = 150
1996 વર્ષમાં : 525 – 400 = 125
1997 વર્ષમાં : 600 – 450 = 150
1998 વર્ષમાં : 650 – 620 = 30
આમ, 1998 વર્ષમાં બંને ભાષાનાં પુસ્તકોનો તફાવત સૌથી ઓછો છે.
(b) આલેખ ઉપરથી જણાય છે કે વર્ષ 1995થી વર્ષ 1998 દરમિયાન અંગ્રેજી પુસ્તકોનું તેમજ હિન્દી પુસ્તકોનું વેચાણ વધ્યું છે.
અંગ્રેજી પુસ્તકોનું વેચાણ 350થી 620 એટલે કે 620 – 350 = 270 વધ્યું છે.
હિન્દી પુસ્તકોનું વેચાણ 500થી 650 એટલે કે 650 – 500 = 150 વધ્યું છે.
હવે, 270 > 150 ∴ અંગ્રેજી પુસ્તકોની માંગ વધી છે.
![]()
પ્રયત્ન કરો : (પાઠ્યપુસ્તક પાન નંબર 74)
એવી સ્થિતિ વિચારીને દરેકના ઓછામાં ઓછા ત્રણ ઉદાહરણ આપો કે જે ચોક્કસ થશે, ને થવાની શક્યતા નથી અને જે થાય પણ ખરી અને ન પણ થાય. એટલે કે પરિસ્થિતિ થવાની કેટલીક તક હોય છે.
(i) એવી વિગત જે ચોક્કસ થશે.
ઉત્તરઃ
(a) સૂર્ય પશ્ચિમ દિશામાં આથમે છે.
(b) આકાશ તરફ ફેકેલી વસ્તુ ધરતી તરફ આવે છે.
(c) રમત રમવાનો પાસો ફેંકતાં પાસા ઉપર 1થી 6માંનો કોઈ એક અંક આવે.
(ii) એવી વિગત જે થવાની શક્યતા નથી.
ઉત્તરઃ
(a) ચંદ્ર ગરમ પ્રકાશ આપે.
(b) એક કલાકમાં 200 કિમી / કલાકની ઝડપે દોડતો માણસ
(c) 5 મીટરની ઊંચાઈનો માણસ
(iii) એવી વિગત જે થાય પણ ખરી અને ન પણ થાય.
ઉત્તરઃ
(a) આવતી કાલે વરસાદ પડશે.
(b) 52 પત્તાંના ઢગમાંથી એક પતું ખેંચતાં તે ગુલામ હોય.
(c) રૂપિયાના સિક્કાને ઉછાળતાં ઉપર છાપ આવે.
પ્રયત્ન કરો : (પાઠ્યપુસ્તક પાન નંબર 75)
(સમૂહમાં કરો.)
1. 100 વખત સિક્કાને ઉછાળો. કેટલી વખત હેડ અને ટેલ તેમાં મળે છે તે શોધી કાઢો.
ઉત્તરઃ
આ પ્રવૃત્તિ છે. ગ્રૂપમાં બેસીને આ પ્રવૃત્તિ કરો.
2. આફતાબ 250 વખત પાસો ફેકે છે અને નીચેનું કોષ્ટક મળે છે. આ માહિતી માટે લંબ આલેખ દોરોઃ
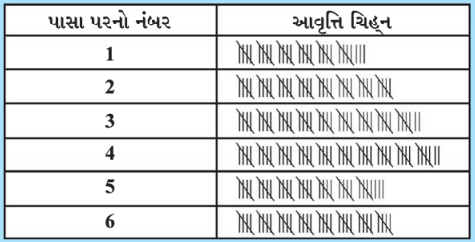
ઉત્તરઃ
ઉપરના કોષ્ટક પરથી લંબ આલેખ રચવા આવૃત્તિની સંખ્યા શોધીને કોષ્ટકમાં દર્શાવીએ.

ઉપર શોધેલ આવૃત્તિ-કોષ્ટક પરથી લંબ આલેખ નીચે પ્રમાણે તૈયાર થાયઃ
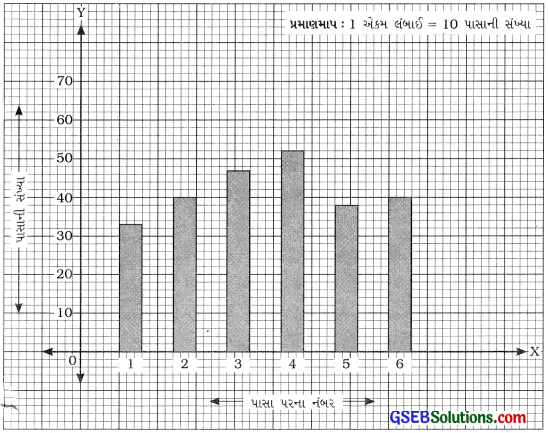
![]()
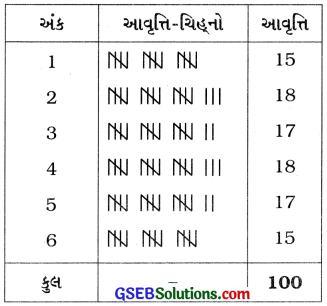
3. પાસાને 100 વખત ફેકો અને માહિતીની નોંધ કરો. 1, 2, 3, 4, 5 અને 6 કેટલી વખત છે તે શોધો.
ઉત્તરઃ
ધારો કે પાસાને 100 વખત ઉછાળતાં મળતા અંકો વિશેની માહિતી નીચે મુજબ છે :