Gujarat Board GSEB Solutions Class 7 Maths Chapter 5 રેખા અને ખૂણા Ex 5.2 Textbook Exercise Questions and Answers.
Gujarat Board Textbook Solutions Class 7 Maths Chapter 5 રેખા અને ખૂણા Ex 5.2
1. નીચેના દરેક વિધાનમાં જે ગુણધર્મનો ઉપયોગ થાય છે તે જણાવો?
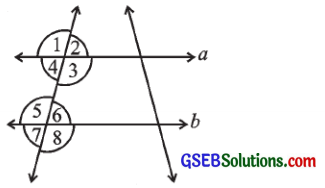
(i) જો a||b, તો ∠1 = ∠5
(ii) જો ∠4 = ∠6, તો a||b
(iii) જો ∠4 + ∠5 = 180°, તો a||b.
ઉત્તરઃ
(i) બે સમાંતર રેખાઓને એક છેદિકા છે, તો તેથી બનતા અનુકોણનાં માપ સરખાં હોય છે.
(ii) જો બે રેખાઓને એક છેદિકા છે, અને તેથી બનતા અંત યુગ્મકોણનાં માપ જો સરખાં હોય, તો તે બે રેખાઓ સમાંતર હોય.
(iii) જો બે રેખાઓને એક છેદિકા છે, અને તેથી બનતા છેદિકાની એક બાજુના બે અંતઃકોણો પૂરકકોણ હોય, તો તે બે રેખાઓ સમાંતર હોય.
2. બાજુની આકૃતિમાંથી કહોઃ
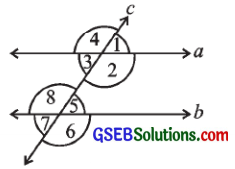
(i) અનુકોણની જોડો
(ii) અંતઃ યુગ્મકોણની જોડો
(iii) છેદિકાની એક જ બાજુના અંતઃકોણની જોડો
(iv) અભિકોણ
ઉત્તરઃ
(i) અનુકોણની જોડ નીચે પ્રમાણે છે :
∠1 અને ∠5; ∠2 અને ∠6; ∠3 અને ∠7; ∠4 અને ∠8
(ii) અંતઃ યુગ્મકોણની જોડ નીચે પ્રમાણે છે :
∠2 અને ∠8; ∠3 અને ∠5
(iii) છેદિકાની એક જ બાજુના અંતઃકોણની જોડ નીચે પ્રમાણે છે :
∠2 અને ∠5; ∠3 અને ∠8
(iv) અભિકોણની જોડ નીચે પ્રમાણે છે :
∠1 અને ∠3; ∠2 અને ∠4; ∠5 અને ∠7; ∠6 અને ∠8
![]()
3. બાજુની આકૃતિમાં p || q છે. અજ્ઞાત ખૂણાઓ શોધો.
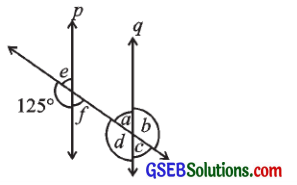
ઉત્તરઃ
અહીં, p || qને છેદિકા છેદે છે.
t અને p છેદે છે. t અને q છેદે છે.
∠e + 125° = 180° (∵ રેખિક જોડના ખૂણા)
∴ ∠e = 180° – 125
∴ ∠e = 55° …. (i)
હવે, ∠e = ∠f (∵ અભિકોણ)
∴ ∠f = 55° …. (ii)
હવે, ∠a = ∠e (∵ અનુકોણ)
∴ ∠a = 55° …. (iii)
જુઓ ∠b = 125° (બાહ્ય યુગ્મકોણ) …(iv)
હવે, ∠b + ∠c = 180° (∵ રેખિક જોડના ખૂણા)
∴ 125° + ∠c = 180°
∴ ∠c = 180° – 125° = 55°… (v)
વળી, ∠d = ∠b (∵ અભિકોણ)
∴ ∠d = 125° (∠b = 125°) …( vi )
આમ, ∠a = 55°, ∠b = 125°, ∠c = 55°
∠d = 125°, ∠e = 55°, ∠f= 55°
4. જો l || m હોય, તો નીચેની દરેક આકૃતિમાં નું મૂલ્ય શોધોઃ
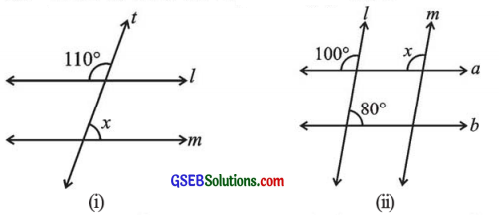
ઉત્તરઃ
(i) અહીં, l || m છે તથા એ l || mની છેદિકા છે.
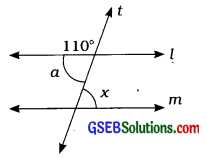
∴ ∠a = ∠x
પરંતુ ∠a + 110° = 180° (∵ રેખિક જોડના ખૂણા)
∴ ∠a = 180° – 110°
∴ ∠a = 70°
હવે, ∠a = 2x (∵ યુગ્મકોણ)
∴ ∠x = 70° (∵ ∠a = 70°)
(ii) અહીં, l || m છે તથા વ એ l || mની છેદિકા છે.
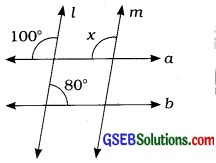
∴ ∠x અને 100° એ અનુકોણની જોડ છે.
∴ ∠x = 100°
![]()
5. બાજુની આકૃતિમાં બંને ખૂણાની બાજુ સમાંતર છે. જો ∠ABC = 70°, તો
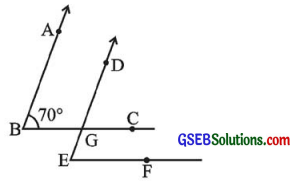
(i) ∠DGC
(ii) ∠DER શોધો.
ઉત્તરઃ
આપેલી આકૃતિમાં બતાવ્યા પ્રમાણે ખૂણાની બાજુ સમાંતર છે.
એટલે કે \(\overleftrightarrow{\mathrm{AB}}\) || \(\overleftrightarrow{\mathrm{ED}}\) અને
\(\overleftrightarrow{\mathrm{BC}}\) || \(\overleftrightarrow{\mathrm{EF}}\) છે.
(i) \(\overleftrightarrow{\mathrm{AB}}\) || \(\overleftrightarrow{\mathrm{ED}}\)ની છેદિકા \(\overleftrightarrow{\mathrm{BC}}\) છે.
∴ ∠DGC = ∠ABC (∵ અનુકોણો)
પણ ∠ABC = 70°
∴ ∠DGC = 70°
(ii) \(\overleftrightarrow{\mathrm{BC}}\) || \(\overleftrightarrow{\mathrm{EF}}\)ની છેદિકા \(\overleftrightarrow{\mathrm{ED}}\) છે.
∴ ∠DEF = ∠DGC (∵ અનુકોણો)
પણ ∠DGC = 70°
∴ ∠DEF = 70°
6. નીચેની આકૃતિઓમાં l અને m સમાંતર છે કે નહીં તે નક્કી કરોઃ
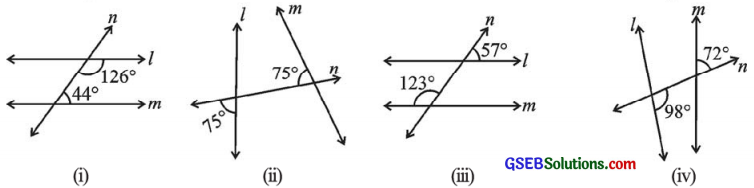
ઉત્તરઃ
(i) આકૃતિ (i)માં જોતાં –
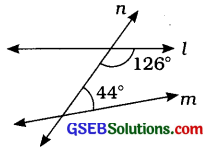
126° + 44° = 170°
પણ 170° ≠ 180°
એટલે કે અહીં l અને mની છેદિકાથી
બનતા છેદિકાની એક જ બાજુના બે અંતઃકોણી પૂરકકોણી નથી.
∴ l અને m સમાંતર રેખાઓ નથી.
(ii) આકૃતિ (ii)માં જોતાં –
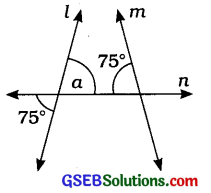
∠a = 75° (∵ અભિકોણ)
હવે, 75° + 75° = 150°
પણ 150° ≠ 180°
એટલે કે અહીં l અને mની છેદિકાથી
બનતા છેદિકાની એક જ બાજુના બે અંતઃકોણો પૂરકકોણો નથી.
∴ l અને m સમાંતર રેખાઓ નથી.
(iii) આકૃતિ (ii)માં જોતાં –
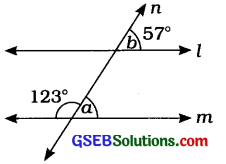
∠a + 123° = 180° (∵ રેખિક જોડના ખૂણા)
∴ ∠a = 180° – 123° = 57°
હવે, ∠a = 57° અને ∠b = 57°
∠a અને ∠b એ l અને m રેખાને n છેદવાથી બનતા સરખા અનુકોણ છે.
∴ l અને m સમાંતર રેખાઓ છે.
![]()
(iv) આકૃતિ (iv)માં જોતાં –
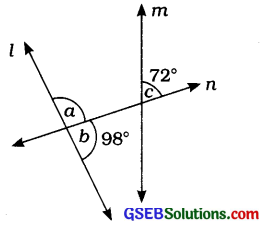
∠a + ∠b = 180° (∵ રેખિક જોડના ખૂણા)
∴ ∠a + 98° = 180°
∴ ∠a = 180° – 98° = 82°
હવે, ∠a અને ∠c એ l અને m રેખાને n એવાથી બનતા અનુકોણ છે. પણ આ ખૂણાનાં માપ સરખાં નથી.
∴ l અને m સમાંતર રેખાઓ નથી.