GSEB Solutions Class 11 Statistics Chapter 5 आवृत्ति वितरण की विषमता Ex 5

Gujarat Board Statistics Class 11 GSEB Solutions Chapter 5 आवृत्ति वितरण की विषमता Ex 5 Textbook Exercise Questions and Answers.

Gujarat Board Textbook Solutions Class 11 Statistics Chapter 5 आवृत्ति वितरण की विषमता Ex 5

विभाग – A

निम्न विकल्प के लिए सही विकल्प का चयन कीजिए ।

प्रश्न 1.
यदि सूचना में भूयिष्ठक अव्याख्यायित हो तो सामान्य संयोगों में उसकी विषमता का विस्तार कितना होगा ?
(A) 0 से 1 तक
(B) -1 से +1 तक
(C) -3 से +3 तक
(D) शून्य
उत्तर :
(C) -3 से +3 तक

प्रश्न 2.
एक आवृत्ति वितरण ऋण विषमतावाला है, तो आवृत्ति वितरण की मध्यका (M) का मूल्य कितना होगा ?
(A) भूयिष्ठक से अधिक
(B) भूयिष्ठक से कम
(C) भूयिष्ठक जितना
(D) भूयिष्ठक के बारे में कुछ नहि कह सकते
उत्तर :
(B) भूयिष्ठक से कम

प्रश्न 3.
दो वितरण के माप निम्न है । निम्न में से कौन-सा विधान सही है ?
वितरण
(i) माध्य = 44, मध्यका = 48 और प्र.विचलन = 20 वितरण
(ii) माध्य = 44, मध्यका = 50 और प्र.विचलन = 24

(A) वितरण (i) और (ii) दोनों समान प्रमाण में विषमतावाला है ।
(B) वितरण (i) यह वितरण (ii) से अधिक विषम है ।
(C) वितरण (i) यह (ii) से कम विषम है ।
(D) दी गई सूचना की विषमता के बारे में कुछ नहि कहा जाता ।
उत्तर :
(C) वितरण (i) यह (ii) से कम विषम है ।

प्रश्न 4.
निम्नानुसार तीन आवृत्ति वितरण के लिए केन्द्रिय स्थिति के दो माप दिये गये है। तीनों आवृत्ति वितरण एक भूयिष्ठकीय है ।
यह तीनों आवृत्ति वितरण में किस प्रकार की विषमता है वह बताइए ।
(i) आवृत्ति वितरण A में भूयिष्ठक = 100 और माध्य = 116
(ii) आवृत्ति वितरण B में मध्यका = 142.8 और माध्य = 142.8
(iii) आवृत्ति वितरण C में मध्यका = 208 और माध्य = 192

(A) आवृत्ति वितरण A संमित, आवृत्ति वितरण B ऋण विषम और आवृत्ति वितरण C धन विषम
(B) आवृत्ति वितरण A ऋण विषम, आवृत्ति वितरण B धन विषम और आवृत्ति वितरण C संमित
(C) आवृत्ति वितरण A धन विषम, आवृत्ति वितरण B संमित और आवृत्ति वितरण C ऋण है ।
(D) आवृत्ति वितरण A धन विषम, आवृत्ति वितरण B ऋण विषम और आवृत्ति वितरण C संमित है ।
उत्तर :
(C) आवृत्ति वितरण A धन विषम, आवृत्ति वितरण B संमित और आवृत्ति वितरण C ऋण है ।

प्रश्न 5.
एक आवृत्ति वितरण में भूयिष्ठक माध्य से 2 अधिक है आवृत्ति वितरण का प्रकार बताइए ।
(A) ऋण विषम है
(B) संमित है
(C) धन विषम है
(D) कुछ नहि कह सकते ।
उत्तर :
(A) ऋण विषम है

प्रश्न 6.
आवृत्ति वितरण में यदि Q₃ + Q₁ = 60 और M = 30 हो, तो उसकी विषमता के लिए कौन-सा विधान सत्य है :
(A) आवृत्ति वितरण अधिक विषम है।
(B) आवृत्ति वितरण कम विषम है।
(C) आवृत्ति वितरण में संमितता की कमी है।
(D) आवृत्ति वितरण संमित है ।
उत्तर :
(D) आवृत्ति वितरण संमित है ।

प्रश्न 7.
एक साधारण असंमित आवृत्ति वितरण में (माध्य – माध्यिका) यह (माध्य – भूयिष्ठक) से कितना गुणा होता है ?
(A) 3
(B) -1
(C) \(\frac{1}{3}[latex]
(D) 0
उत्तर :
(C) [latex]\frac{1}{3}[latex]

प्रश्न 8.
ऋण विषम आवृत्ति वितरण के लिए कौन-सा विधान असत्य है ?
(A) माध्य का मूल्य माध्यिका और भूयिष्ठक के मूल्य से कम होती है ।
(B) तृतीय चतुर्थक और माध्यिका के बीच का मूल्य, माध्यिका और प्रथम चतुर्थक के बीच का अंतर से कम होता है ।
(C) आवृत्ति वक्र में शिरा बाँयी ओर खींचा हुआ होता है ।
(D) तृतीय चतुर्थक और माध्यिका के बीच का मूल्य का अंतर, माध्यिका और प्रथम चतुर्थक के बीच का अंतर के मूल्य से अधिक होता है ।
उत्तर :
(D) तृतीय चतुर्थक और माध्यिका के बीच का मूल्य का अंतर, माध्यिका और प्रथम चतुर्थक के बीच का अंतर के मूल्य से अधिक होता है ।

प्रश्न 9.
संमित आवृत्ति वितरण के लिए कौन-सा विधान सत्य है ? ।
(A) Q₃ = 2M – Q₁
(B) Q₂ – Q₃ = Q₂ – Q₁
(C) Q₃ + Q₁ > 2M
(D) Q₃ + Q₁ < 2M
उत्तर :
(A) Q₃ = 2M – Q₁

प्रश्न 10.
यदि (M – [latex]\overline{\mathrm{X}}\)) = – \(\frac{1}{2}\)S हो, तो j का मूल्य कितना होगा ?
(A) \(\frac{1}{3}\)
(B) \(\frac{3}{2}\)
(C) – 1.5
(D) 0.15
उत्तर :
(B) \(\frac{3}{2}\)

प्रश्न 11.
(i) ऋण विषम आवृत्ति वितरण में और (ii) धन विषम आवृत्ति वितरण में केन्द्रिय प्रवृति के कौन से माप का मूल्य सब अधिक होता है ?
(A) (i) माध्य (ii) भूयिष्ठक
(B) (i) माध्यिका (ii) भूयिष्ठक
(C) (i) भूयिष्ठक (ii) माध्य
(D) माध्य, माध्यिका, भूयिष्ठक के मूल्य के लिए कुछ नहीं कहा जाता ।
उत्तर :
(C) (i) भूयिष्ठक (ii) माध्य

प्रश्न 12.
वितरण X की विषमतांक -0.99 और वितरण Y की विषमतांक 0.90 हो, तो कौन-सा वितरण अधिक विषम है ?
(A) वितरण X अधिक विषम है ।
(B) वितरण Y अधिक विषम है ।
(C) कुछ नहि कहा जाता
(D) वितरण X और Y की विषमता समान है ।
उत्तर :
(A) वितरण X अधिक विषम है ।

प्रश्न 13.
निम्न में से कौन-सा विधान असत्य है ?
(A) Q₃ + Q₁ > 2M हो, तो वितरण में धन विषमता है ।
(B) स्थानीय औसत के उपयोग से बाउली का विषमतांक ज्ञात किया जाता है ।
(C) कार्ल पियर्सन की विधि में चर की इकाई का प्रभाव दूर करने के लिए निरपेक्ष माप को प्रमाप विचलन से भाग दिया जाता है । जब कि बाउली की विधि में निरपेक्ष माप को चतुर्थक के अंतर से भाग दिया जाता है ।
(D) विषम आवृत्ति वितरण में भूयिष्ठक के दोनों ओर समान दूरी पर आये अवलोकन में आवृत्ति समान रीति से वितरीत हुई है ।
उत्तर :
(D) विषम आवृत्ति वितरण में भूयिष्ठक के दोनों ओर समान दूरी पर आये अवलोकन में आवृत्ति समान रीति से वितरीत हुई है ।

प्रश्न 14.
निम्न में से कौन-सा विधान सत्य है ? बताइए ।
(A) यदि समष्टि के अवलोकन भूयिष्ठक के मूल्य से दोनों और समान रीति से वितरीत हो उसे विषम आवृत्ति वितरण कहते है।
(B) माध्यिका से अंतिम चतुर्थकों का अंतर के मूल्य संमित आवृत्ति वितरण में समान होते है ।
(C) यदि S_K > 0, तो \(\overline{\mathrm{X}}\) > M और \(\overline{\mathrm{X}}\) < M_O होगा ।
(D) यदि S_K < 0, हो तो \(\overline{\mathrm{X}}\) < M और \(\overline{\mathrm{X}}\) > M_O होगा ।
उत्तर :
(B) माध्यिका से अंतिम चतुर्थकों का अंतर के मूल्य संमित आवृत्ति वितरण में समान होते है ।

विभाग – B

निम्न प्रश्नों के उत्तर एक वाक्य में दीजिए ।

प्रश्न 1.
विषमता अर्थात् क्या ?
उत्तर :
सममितियता का अभाव अर्थात् विषमता ।

प्रश्न 2.
संमित आवृत्ति वितरण किसे कहते है ?
उत्तर :
यदि समष्टि के अवलोकन भूयिष्ठक के मूल्य से दोनों ओर समान रीति से वितरित हुए हो एसे आवृत्ति वितरण को संमित आवृत्ति वितरण कहते है।

प्रश्न 3.
आवृत्ति वितरण में विषमता है ऐसा कब कहा जाता है ?
उत्तर :
संमितता या सुडोलता की कमीवाले आवृत्ति वितरण में विषमता है ऐसा कहेंगे ।

प्रश्न 4.
विषम आवृत्ति वितरण में माध्यिका के स्थान के बारे में क्या कहोगे ?
उत्तर :
विषम आवृत्ति वितरण में माध्यिका माध्य और भूयिष्ठक के बीच प्राप्त होगा । \(\bar{x}\) > M > M _O अथवा \(\bar{x}\) < M < M_O

प्रश्न 5.
आवृत्तिवक्र द्वारा विषमता कैसे निश्चित होता है समझाइए ।
उत्तर :
आवृत्तिवक्र का किनार किस तरफ खिंचा हुआ है उस पर से विषमता धन है या ऋण वह निश्चित होता है ।

प्रश्न 6.
विषमतांक अर्थात् क्या ? विषमतांक की किंमत का विस्तार बताइए ।
उत्तर :
विषमता के सापेक्ष माप को विषमतांक कहते है । उसका विस्तार -1 से +1 और -3 से +3 प्राप्त होता है ।

प्रश्न 7.
कार्लपियर्सन की पद्धति में विषमता का माप ज्ञात करने के लिए कौन-कौन से मापों का उपयोग किया जाता है ?
उत्तर :
कार्ल पियर्सन की पद्धति में विषमता ज्ञात करने के लिए माध्य, माध्यिका, भूयिष्ठक और प्रमाप विचलन का उपयोग किया जाता है ।

प्रश्न 8.
बाउली की पद्धति में विषमता का माप प्राप्त करने का आधार बताइए ।
उत्तर :
बाउली का माप चतुर्थकों की स्थिति पर आधारित है ।

प्रश्न 9.
कौन-सी पद्धति से प्राप्त विषमतांक का मूल्य अधिक विश्वसनीय है ?
उत्तर :
कार्लपियर्सन की पद्धति से प्राप्त विषमतांक का मूल्य अधिक विश्वसनीय है ।

प्रश्न 10.
विषमतांक सापेक्ष माप है या निरपेक्ष माप ? कारण दीजिए।
उत्तर :
विषमतांक सापेक्ष माप है । क्योंकि सापेक्ष माप प्राप्त करने के लिए विषमता के निरपेक्ष माप को अपकिरण के योग्य माप से भाग दिया जाता है।

प्रश्न 11.
जब खुल्ला शिरावाला आवृत्ति वितरण और एक से अधिक भूयिष्ठक हो तब विषमतांक कौन से सूत्र से प्राप्त करोगे?
उत्तर :
एक से अधिक भूयिष्ठकवाला आवृत्ति वितरण हो तब भूयिष्ठक के स्थान पर माध्यिका ज्ञात करके निम्न सूत्र का उपयोग करेंगे ।
j = \(\frac{3(\overline{\mathrm{X}}-\mathrm{M})}{\mathrm{S}}\)

प्रश्न 12.
असमान वर्गलम्बाईवाला आवृत्ति वितरण में कार्लपियर्सन पद्धति से विषमतांक का मूल्य का विस्तार बताइए ।
उत्तर :
असमान वर्गलम्बाईवाला आवृत्ति वितरण में कार्लपियर्सन पद्धति से विषमतांक का मूल्य -3 से +3 के बीच प्राप्त होगा ।

प्रश्न 13.
एक आवृत्ति वितरण के तीन चतुर्थक 42, 36 और 40 है, तो आवृत्ति वितरण का प्रकार बताइए ।
उत्तर :
यहा Q₁ = 36, Q₃ = 42, M = 40 होगा । Q₃ – M > M – Q₁ है इसलिए ऋण विषमतावाला आवृत्ति वितरण है ।

प्रश्न 14.
यदि किसी आवृत्ति वितरण में (Q₃ – Q₂) < (Q₂ – Q₁) हो, तो आवृत्ति वितरण का प्रकार बताइए ।
उत्तर :
ऋण आवृत्ति वितरण होगा ।

प्रश्न 15.
एक सूचना का आवृत्ति वितरण का माध्य उसकी मध्यका से 2 जितना कम है, तो आवृत्ति वितरण का प्रकार बताइए।
उत्तर :
यहाँ \(\overline{\mathrm{X}}\) < M है इसलिए ऋण विषमवाला आवृत्ति वितरण है ।

प्रश्न 16.
एक आवृत्ति वितरण के लिए Q₃ + Q₁ = 125 और M = 62.5 है, तो आवृत्ति वितरण की विषमता के बारे में क्या कह सकते हो ?
उत्तर :
यहाँ Q₃ + Q₁ – 2M = 0 होता है । 125 – 2 × 62.5 = 125 – 125 = 0 इसलिए संमित आवृत्ति वितरण है ।

प्रश्न 17.
एक आवृत्ति वितरण में \(\overline{\mathrm{X}}\) = M = M_O = 48 है । आवृत्ति वितरण के बारे में क्या कह सकते है ?
उत्तर :
यहाँ माध्य, माध्यिका, भूयिष्ठक के मूल्य समान है इसलिए संमित आवृत्ति वितरण है ।

विभाग – C

निम्न प्रश्नों के उत्तर दीजिए ।

प्रश्न 1.
विषमता के प्रकार कितने है ? कौन कौन से बताइए ।
उत्तर :
विषमता के मुख्य दो प्रकार है :

1. धन विषमता
2. ऋणात्मक विषमता

प्रश्न 2.
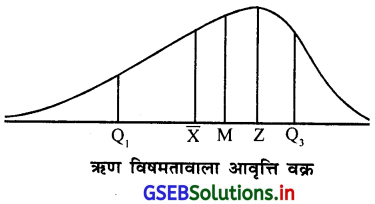
विषमता के प्रकार, औसत के माप तथा चतुर्थकों के स्थान आकृति में दर्शाइए ।
उत्तर :
(i) धन विषमता में औसत के माप :

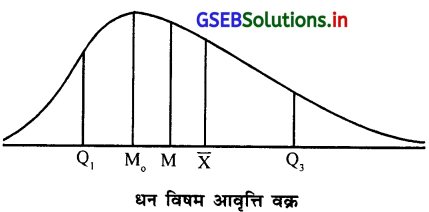
(ii) ऋण विषमता में औसत के माप :

प्रश्न 3.
संमित आवृत्ति वितरण के कोई भी दो लक्षण बताइए ।
उत्तर :
संमित आवृत्ति वितरण में निम्न लक्षण दृष्टिगोचर होता है :

1. सममितीय आवृत्ति वितरण का आवृत्ति वक्र संपूर्ण घंटाकार का होता है ।
2. सममितीय आवृत्ति वितरण में माध्य, मध्यका और भूयिष्ठक के मूल्य समान होते है, अर्थात् \(\bar{x}\) = M = M_O

प्रश्न 4.
विषम आवृत्ति वितरण के कोई दो लक्षण बताइए ।
उत्तर :
विषम आवृत्ति वितरण में निम्न लक्षण दिखाई देते है :

1. जिस आवृत्ति वितरण का माध्य, मध्यका और भूयिष्ठक के मूल्य समान न हो अर्थात् \(\bar{x}\) ≠ M ≠ M_O
2. जिस आवृत्ति वितरण में चतुर्थक मध्यका से समान अन्तर पर न आये हो अर्थात् Q₃ – M ≠ M – Q₁ होगा ।

प्रश्न 5.
एक आवृत्ति वितरण की विषमता S_K = – 2.8 है । यदि उसका भूयिष्ठक 48.8 हो, तो माध्य ज्ञात करो ।
उत्तर :
SK = \(\overline{\mathrm{X}}\) – M_O M_O = 48.8 दिया है ।
∴ – 2.8 = \(\overline{\mathrm{X}}\) – 48.8
∴ – 2.8 + 48.8 = \(\overline{\mathrm{X}}\)
∴ \(\overline{\mathrm{X}}\) = 46 माध्य = 46

प्रश्न 6.
संमित आवृत्ति वितरण में दो अंतिम चतुर्थक का योग 138 है, तो उसकी मध्यका ज्ञात करो ।
उत्तर :
संमित आवृत्ति वितरण में विषमता SK = 0 होगा और Q₃ + Q₁ = 138 है ।
∴ SK = Q₃ + Q₁ – 2M
O = 138 – 2M
∴ 2M = 138
∴ M = \(\frac{138}{2}\)
∴ M = 69

प्रश्न 7.
एक धन विषम आवृत्ति वितरण का विषमतांक 0.75 है । यदि प्र. विचलन 20 और माध्य 37.50 हो, तो M ज्ञात करो।
उत्तर :
यहाँ j = 0.75, S = 20, \(\bar{X}\) = 37.50 है ।
∴ j = \(\frac{3(\bar{X}-M)}{S}\)
0.75 = \(\frac{3(37.50-M)}{20}\) \(\frac{0.75 \times 20}{3}\) = 37.50 – M
5 = 37.50 – M
∴ M = 37.50 – 5
∴ M = 32.50

प्रश्न 8.
एक आवृत्ति वितरण का माध्य उसकी मध्यका से 3 जितना अधिक है । यदि आवृत्ति वितरण का विषमतांक 0.75 हो, तो प्रमाप विचलन ज्ञात करो ।
उत्तर :
यहाँ \(\overline{\mathrm{X}}\) – M = 3, j = 0.75
∴ j = \(\frac{3(\overline{\mathrm{X}}-\mathrm{M})}{\mathrm{S}}\)
0.75 = \(\frac{3(3)}{S}\)
∴ S = \(\frac{9}{0.75}\)
∴ S = 12

प्रश्न 9.
एक आवृत्ति वितरण में Q₃ – Q₂ = 2 (Q₂ – Q₁) हो, तो j ज्ञात करो ।
उत्तर :
j = \(\frac{\left(Q_3-Q_2\right)-\left(Q_2-Q_1\right)}{\left(Q_3-Q_2\right)+\left(Q_2-Q_1\right)}\)
Q₃ – Q₂ के स्थान पर 2 (Q₂ – Q₁) रखने पर
∴ j = \(\frac{2\left(Q_2-Q_1\right)-1\left(Q_2-Q_1\right)}{2\left(Q_2-Q_1\right)+1\left(Q_2-Q_1\right)}\) = \(\frac {1}{2}\)
j = 0.33

प्रश्न 10.
एक आवृत्ति वितरण में SK = – 6.6 और चतुर्थक विचलन = 22 हो, तो j ज्ञात करो ।
उत्तर :
SK = Q₃ + Q₁ – 2M
-6.6 = Q₃ + Q₁ – 2M
Qd = \(\frac{\mathrm{Q}_3-\mathrm{Q}_1}{2}\)
22 × 2 = Q₃ – Q₁
∴ Q₃ – Q₁ = 44
∴ j = \(\frac{\mathrm{Q}_3+\mathrm{Q}_1-2 \mathrm{M}}{\mathrm{Q}_3-\mathrm{Q}_1}=\frac{-6.6}{44}\)
j = – 0.15

प्रश्न 11.
एक विषम आवृत्ति वितरण में माध्य = 40, भूयिष्ठक = 46, Q₃ + Q₁ = 76 और Q₃ – Q₁ = 20 है, तो बाउली का विषमतांक ज्ञात करो ।
उत्तर :
बाउली का विषमतांक ज्ञात करने के लिए भूयिष्ठक का अनुमानिततायुक्त सूत्र M_O = 3M – 2\(\bar{X}\) से मध्यका ज्ञात करेंगे ।
M_O = 3M – 2\(\bar{X}\)
46 = 3M – 2 × 40
46 + 80 = 3M
∴ 3M = 126
M = \(\frac{126}{3}\)
M = 42

j = \(\frac{\mathrm{Q}_3+\mathrm{Q}_1-2 \mathrm{M}}{\mathrm{Q}_3-\mathrm{Q}_1}\)
= \(\frac{76-2 \times 42}{20}\)
= \(\frac{76-84}{20}\)
= \(\frac{-8}{20}\)
∴ j = – 0.4 3

प्रश्न 12.
‘बाउली की पद्धति से प्राप्त विषमतांक कार्लपियर्सन की पद्धति से प्राप्त विषमतांक से अधिक विश्वसनीय नहि है ।’ समझाइए ।
उत्तर :
कार्लपियर्सन की विधि की गणना में माध्य और प्रमाप विचलन जैसे मापों का उपयोग किया जाता है और उसकी गणना में सभी अवलोकन का उपयोग किया जाता है जब कि बाउली का सूत्र चतुर्थक पर आधारित है और उसकी गणना में मध्य के 50% अवलोकन का ही उपयोग होता है इसलिए बाउली की पद्धति से कार्लपियर्सन की पद्धति अधिक विश्वसनीय है ।

प्रश्न 13.
एक आवृत्ति वितरण का तीनों चतुर्थक 76, 98 और 40 है, तो j ज्ञात करो और प्रकार बताइए ।
उत्तर :
यहाँ Q₃ = 98, Q₁ = 40, M = 76
j = \(\frac{\mathrm{Q}_3+\mathrm{Q}_1-2 \mathrm{M}}{\mathrm{Q}_3-\mathrm{Q}_1}\)
= \(\frac{98+40-2 \times 76}{98-40}\) = \(\frac{138-152}{58}=\frac{-14}{58}\)
= – 0.24
आवृत्ति वितरण में ऋण विषमता है ।

प्रश्न 14.
एक आवृत्ति वितरण का j= 0.85 है । यदि उसका माध्य भूयिष्ठक से 3.4 जितना अधिक हो, तो उसका विचरण ज्ञात करो ।
उत्तर :
माध्य भूयिष्ठिक से 3.4 जितना अधिक है ।
∴ \(\overline{\mathrm{X}}\) – Mo = + 3.4 .
j = \(\frac{X-M_0}{S}\)
0.85 = \(\frac{3.4}{\mathrm{~S}}\)
S = \(\frac{3.4}{0.85}\)
∴ = 4
∴ विचरण S² = 4²
∴ विचरण S² = 16

प्रश्न 15.
एक आवृत्ति वितरण में \(\overline{\mathrm{X}}\) + M_O = 82, \(\overline{\mathrm{X}}\) = 44 और S = 12 हो, तो j ज्ञात करो ।
उत्तर :
j = \(\frac{\bar{X}-M_0}{S}\)
= \(\frac{44-38}{12}\)
= \(\frac{6}{12}\)
j = 0.5
यहाँ \(\overline{\mathrm{X}}\) + M_O = 82
44 + M_O = 82
∴ M_O = 82 – 44
M_O = 38

विभाग – D

निम्न प्रश्नों के उत्तर दीजिए ।

प्रश्न 1.
कार्लपियर्सन की विषमतांक ज्ञात करने की विधि संक्षिप्त में समझाइए ।
उत्तर :
विषम आवृत्ति वितरण में माध्य, मध्यका और भूयिष्ठक के मूल्य समान नहीं होते है और मध्यका का मूल्य हमेशां माध्य और भूयिष्ठक के बीच होता है । इसलिए सामान्य रूप से माध्य और भूयिष्ठक के बीच के अंतर को विषमता के माप के रूप में लिया जाता है । अर्थात् SK = \(\overline{\mathrm{X}}\) – M_O इस अन्तर को अपकिरण का श्रेष्ठ माप प्रमाप विचलन से भाग देने पर कार्लपियर्सन का विषमतांक प्राप्त होता है ।
j = \(\frac{\bar{X}-M_0}{S}\)

जब आवृत्ति वितरण में एक से अधिक भूयिष्ठक हो तब कार्लपियर्सन का विषमता और विषमतांक ज्ञात करने के लिए अनुमानितता युक्त सूत्र का उपयोग करेंगे ।

M_O = 3M – 2\(\overline{\mathrm{X}}\)
∴ 3(\(\overline{\mathrm{X}}\) – M)
j = \(\frac{3(\bar{X}-M)}{S}\)

प्रश्न 2.
विषमतांक ज्ञात करने की बाउली की विधि पर टिप्पणी लिखिए ।
उत्तर :
बाउली का सूत्र चतुर्थक पर आधारित है । विषम आवृत्ति वितरण में दोनों चतुर्थक मध्यका से समान अंतर पर होता नहि है । विषमता का निरपेक्ष माप SK प्राप्त करने के लिए Q₃ – M और M – Q का उपयोग करेंगे ।
अर्थात् SK = (Q₃ – M) – (M – Q₁)
∴ SK = Q₃ + Q₁ – 2M
यदि आवृत्ति वितरण की विषमतांक ज्ञात करने के लिए
j = \(\frac{\left(Q_3-M\right)-\left(M-Q_1\right)}{\left(Q_3-M\right)+\left(M-Q_1\right)}\)
j = \(\frac{\mathrm{Q}_3+\mathrm{Q}_1-2 \mathrm{M}}{\mathrm{Q}_3-\mathrm{Q}_1}\)

प्रश्न 3.
कार्लपियर्सन का सूत्र j = 3(\(\frac{\bar{x}-M}{S}\)) का उपयोग कौन से संयोगों में करके विषमतांक ज्ञात किया जाता है बताइए ।
उत्तर :
जब आवृत्ति वितरण में भूयिष्ठक का मूल्य एक से अधिक हो अथवा मिश्र आवृत्ति वितरण हो या आवृत्ति वितरण में वर्गलम्बाई असमान हो तब j = 3 (\(\frac{\overline{\mathrm{X}}-\mathrm{M}}{\mathrm{S}}\)) सूत्र का उपयोग करके विषमतांक ज्ञात किया जाता है ।

प्रश्न 4.
धन विषमता और ऋण विषमता का अंतर पद्धति सह और आकृति सह समझाइए ।
उत्तर :
धन विषमता की आकृति :

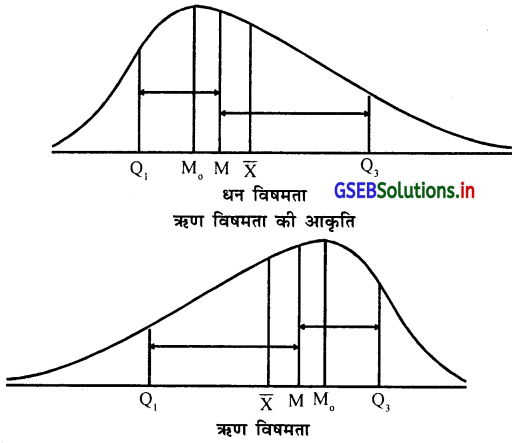
धन विषमता और ऋण विषमता का अंतर :

धन विषमता	ऋण विषमता
(1) इस में माध्य, मध्यका और भूयिष्ठक के मूल्य उतरते क्रम में होते है अर्थात् \(\bar{x}\) > M > MO	(1) इस में माध्य, मध्यका और भूयिष्ठक के मूल्य चढ़ते क्रम में होते है । अर्थात् \(\bar{x}\) < M < MO
(2) उसमें तृतीय चतुर्थक और मध्यक के बीच के अंतर से मध्यका और प्रथम चतुर्थक के बीच का अन्तर कम होता है । अर्थात् Q3 – M > M – Q1	(2) इसमें तृतीय चतुर्थक और मध्यका के बीच के अंतर मध्यका और प्रथम चतुर्थक के अन्तर से कम होता है । अर्थात् Q3 – M < M – Q1
(3) इसमें आवृत्तिवक्र के दाहिनी ओर की किनार अधिक खिची होती है ।	(3) इसमें आवत्तिवक्र का किनार बायी ओर खिचा हआ होता है ।

प्रश्न 5.
निम्न में से कौन-सी समष्टि संमितता के अधिक समीप है ?
समष्टि A : \(\bar{x}\) = 56, Mo = 60 और S = 24
समष्टि B : \(\bar{x}\) = 56, M = 60 और S = 30
उत्तर :

समष्टि A
j = \(\frac{\bar{X}-M_0}{S}\)
= \(\frac{56-60}{24}\)
= \(\frac{-4}{24}\)
= – 0.17

समष्टि B
j = \(\frac{3(\bar{X}-M)}{S}\)
= \(\frac{3(56-60)}{30}\)
= \(\frac{3(-4)}{30}\)
= – 0.4

प्रश्न 6.
यहाँ समष्टि A में विषमतांक B की अपेक्षा कम है इसलिए समष्टि A संमितियता के अधिक समीप है । निम्न सूचना पर से योग्य पद्धति का उपयोग करके विषमतांक. ज्ञात करो और समष्टि A और समष्टि B में से कौनसा समूह अधिक विषम है वह निश्चित कीजिए ।
समष्टि A : 4Q₁ = 3Q₂ = 2Q₃ = 144
समष्टि B : Q₁ = 34.8, Q₂ = 45.5 और Q₃ = 70
उत्तर :


j = 0.33

समष्टि B का विषमतांक समष्टि A से अधिक है इसलिए समष्टि B विषमता के अधिक समीप है अर्थात् B विषम है ।

प्रश्न 7.
एक आवृत्ति वितरण में मध्यका से तृतीय चतुर्थक 128 जितना अंतर पर और मध्यका से प्रथम चतुर्थक 11.2 जितना अंतर पर है, तो विषमता और विषमतांक ज्ञात करो ।
उत्तर :
यहाँ Q₃ – M = 12.8 और M – Q₁ = 11.2
∴ SK = (Q₃ – M) – (M – Q₁)
= 12.8 – 11.2 = 1.6
∴ j = \(\frac{\left(Q_3-M\right)-\left(M-Q_1\right)}{\left(Q_3-M\right)+\left(M-Q_1\right)}\)
= \(\frac{12.8-11.2}{12.8+11.2}=\frac{1.6}{24}\)
= 0.07

प्रश्न 8.
एक आवृत्ति वितरण का C.V = 25%, \(\bar{X}\) = 32 और M = 32.2 है, तो विषमतांक ज्ञात करो ।
उत्तर :
C.V = \(\frac{S}{\bar{X}}\) × 100
25 = \(\frac{S}{32}\) × 100
∴ = \(\frac{25 \times 32}{100}\) = S
∴ S = \(\frac{800}{100}\)
S = 8

∴ j = \(\frac{\overline{\mathrm{X}}-\mathrm{M}_0}{\mathrm{~S}}\)
= \(\frac{32-32.2}{8}\)
= \(\frac{-0.2}{8}\)
j = – 0.025

प्रश्न 9.
निम्न सूचना का उपयोग करके विषमतांक ज्ञात करो ।
n = 20, Σx = 640, Σx² = 20,800 और M = 32.2
उत्तर :
\(\frac{\Sigma x}{n}=\frac{640}{20}\) = 32

j = – 0.15

प्रश्न 10.
एक सूचना के लिए कार्लपियर्सन का j = – 0.60 है । यदि \(\overline{\mathrm{x}}\) = 60, S = 10 हो, तो M और M_O ज्ञात करो ।
उत्तर :

-0.60 × 10 = 3(60 – M) = \(\frac{-6}{3}\) = 60 – M
– 2 + M = 60
∴ M = 60 + 2
∴ M = 62

प्रश्न 11.
एक आवृत्ति वितरण के लिए कार्लपियर्सन की विषमता 8 और विषमतांक = \(\frac{4}{6}\) है । यदि \(\overline{\mathrm{X}}\) = 64 हो, तो उसका मध्यका और विचरण गुणांक ज्ञात करो ।

यहाँ SK = 8 और j = \(\frac{4}{6}\), \(\overline{\mathrm{X}}\) = 64 दिया है ।

∴ C.V. = 18.75

प्रश्न 12.
एक आवृत्ति वितरण में Q₃ + Q₁ = 1.5 M और 3(Q₃ – Q₁) = 2M हो, तो j ज्ञात करो ।
उत्तर :
यहाँ Q₃ + Q₁ = 1.5 M रखने पर और Q₃ – Q₁ = =\(\frac{2 \mathrm{M}}{3}\) रखने पर
∴ j = \(\frac{\mathrm{Q}_3+\mathrm{Q}_1-2 \mathrm{M}}{\mathrm{Q}_3-\mathrm{Q}_1}=\frac{1.5-2 \mathrm{M}}{0.67 \mathrm{M}}=\frac{-0.5 \mathrm{M}}{0.67 \mathrm{M}}\)
∴ j = – 0.75

प्रश्न 13.
एक आवृत्ति वितरण के लिए 4\(\overline{\mathrm{X}}\) = 6M_O = 144, S = 64 और Q₃ + Q₁ = 6(Q₃ – Q₁) = 60 हो, तो कार्लपियर्सन और बाउली का j ज्ञात करो ।
उत्तर :

विभाग – E

निम्न प्रश्नों के उत्तर दीजिए ।

प्रश्न 1.
विषम आवृत्ति वितरण की परिभाषा दीजिए और उसके लक्षण बताइए ।
उत्तर :
सममितियता का अभाव अर्थात् विषमता । उसके लक्षण निम्नलिखित है :

1. जिस आवृत्ति वितरण का आवृत्तिवक्र संपूर्ण घंटाकार का न हो ऐसा आवृत्ति वितरण विषम है ।
2. जिस आवृत्ति वितरण का माध्य, मध्यका और भूयिष्ठक समान नहीं अर्थात् \(\overline{\mathrm{X}}\) # M # M_O वह विषम आवृत्ति वितरण है ।
3. जिस आवृत्ति वितरण में चतुर्थक मध्यका से समान अन्तर पर न आये हो उस आवृत्ति वितरण विषम है ऐसा कहेंगे । .
4. यदि मध्य में आये वर्ग का महत्तम आवृत्ति से दोनों ओर समान अन्तर पर आये वर्गों की आवृत्तियाँ समान न हो वह
   विषम आवृत्ति वितरण है ।
5. जिस आवृत्तिवक्र का आवृत्तिवक्र के दोनों किनार अधिक खिचा हुआ होता है ।

प्रश्न 2.
संमित आवृत्ति वितरण की परिभाषा दीजिए और उसके लक्षण बताइए ।
उत्तर :
जिस आवृत्ति वितरण का आवृत्तिवक्र संपूर्ण घंटाकार स्वरूप का हो उसे संमित आवृत्ति वितरण कहते है । संमित आवृत्ति
वितरण की विशेषताएँ (लक्षण) निम्नलिखित रूप से है :

1. संमित आवृत्ति वितरण में माध्य, मध्यका और भूयिष्ठक के मूल्य समान होते है अर्थात् \(\bar{x}\) = M = Z .
2. संमित आवृत्ति वितरण में प्रथम चतुर्थक और तृतीय चतुर्थक मध्यका से समान अन्तर पर स्थित होता है । अर्थात् Q₃ – M = M – Q₁
3. उसमें महत्तम आवृत्ति बीच के वर्ग में होती है और बीच के वर्ग के दोनों ओर के समान दूरी पर आये वर्गों में आवृत्तियाँ समान होती है। उसका आवृत्तिवक्र घंटाकार स्वरूप का होता है ।

प्रश्न 3.
विषमतांक के लिए कार्लपियर्सन और बाउली की विधि का अंतर दीजिए ।
उत्तर :

कार्लपियर्सन की विधि	बाउली की पद्धति
(1) कार्ल पियर्सन की विधि माध्य, मध्यका, भूयिष्ठक और प्रमाप विचलन पर आधारित है ।	(1) बाउली की विधि चतुर्थक पर आधारित है ।
(2) कार्लपियर्सन की विधि में माध्य और प्रमाप विचलन की गणना में सभी अवलोकनों का उपयोग होता है ।	(2) चतुर्थक की गणना में मध्य के 50% अवलोकनों का उपयोग होता है ।
(3) कार्ल पियर्सन की विधि में माध्य और प्रमाप विचलन का उपयोग होता है इसलिए यह विधि बाउली की अपेक्षा अधिक विश्वसनीय है ।	(3) बाउली की विधि में सिर्फ मध्य के 50% अवलोकनों का उपयोग होता है इसलिए कार्लपियर्सन जितनी विश्वसनीय नहीं है ।

प्रश्न 4.
विषमता और विषमतांक समझाइए ।
उत्तर :
विषमता : विषमता अर्थात् आवृत्ति वितरण में सममितियता की कमी
वैषमतांक : वैषमतांक अर्थात् विषमता का सापेक्ष माप

प्रश्न 5.
विषमता के अभ्यास के मुख्य उद्देश्य क्या-क्या है ?
उत्तर :
विषमता के अभ्यास के मुख्य उद्देश्य निम्न है :

1. विषमता के अभ्यास से दो संबंधित सूचना की तुलना कर सकते है ।
2. कार्लपियर्सन और बाउली की पद्धति में विषमतांक समान प्राप्त होता नहि है ।

प्रश्न 6.
दो उत्पादक पेढ़ीओं के मासिक वेतन का उत्पादन का आवृत्ति वितरण के माप निम्न है । बाउली और कार्लपियर्सन की विधि से विषमतांक ज्ञात करके दोनों पेढ़ी की तुलना करो ।

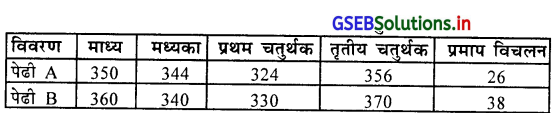
उत्तर :

कार्लपियर्सन की पद्धति में पेढ़ी A से B अधिक विषम है । बाउली की पद्धति में पेढ़ी A से पेढ़ी B अधिक विषम है ।

प्रश्न 7.
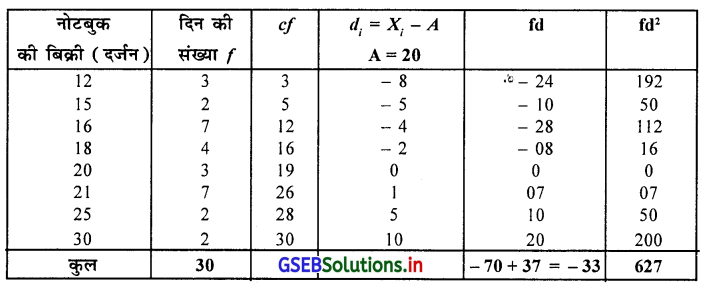
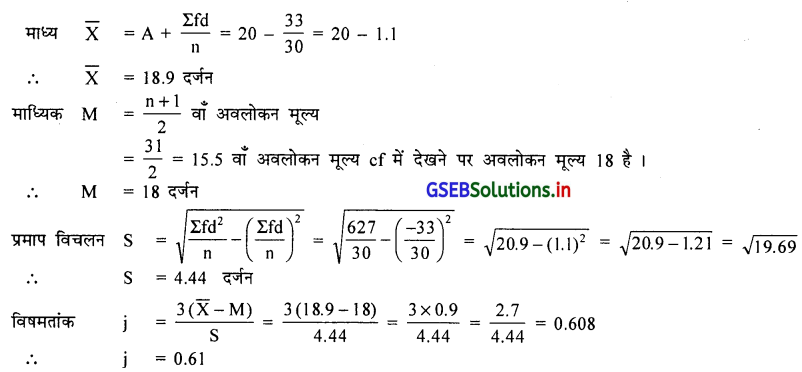
वर्ष 2014 के जून मास के दौरान एक स्टेशनरी की दुकान में हुई नोटबुक की बिक्री का आवृत्ति वितरण निम्नानुसार है, तो उस पर से कार्लपियर्सन की पद्धति से विषमतांक ज्ञात करो ।

उत्तर :

आवृत्ति वितरण में द्वि भूयिष्ठक है इसलिए विषमतांक ज्ञात करने के लिए माध्य, मध्यका और प्रमाप विचलन की गणना करेंगे ।

प्रश्न 8.
500 स्टेपलर के एक ऐसे 50 पेकेट की जाँच करने पर दोषयुक्त स्टेपलर की सूचना निम्नानुसार है। उस पर से कार्लपियर्सन की पद्धति से विषमतांक ज्ञात करो ।

उत्तर :
आवृत्ति वितरण एक भूयिष्ठिकवाला है इसलिए विषमतांक ज्ञात करने के लिए माध्य, भूयिष्ठक और प्रमाप विचलन की गणना करेंगे ।

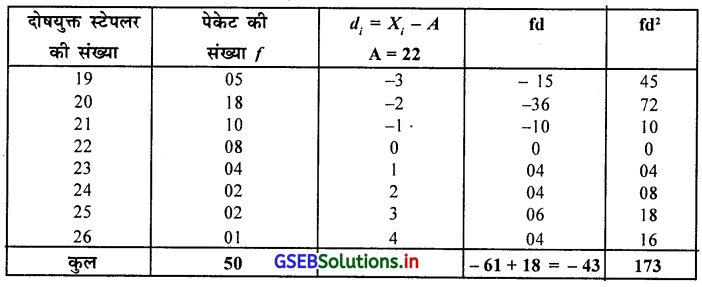
माध्य \(\bar{X}\) = A + \(\frac{\Sigma \mathrm{fd}}{\mathrm{n}}\) = 22 + \(\frac{-43}{50}\) = 22 – 0.86
∴ \(\bar{X}\) = 21.14 इकाई
महत्तम आवृति 18 के अनुरूप अवलोकन 20 है । इसलिए भूयिष्ठक 20 है ।
∴ M_O = 20 इकाई
प्रमाप विचलन S = \(\sqrt{\frac{\Sigma \mathrm{fd}^2}{\mathrm{n}}-\left(\frac{\Sigma \mathrm{fd}}{\mathrm{n}}\right)^2}\) = \(\sqrt{\frac{173}{50}-\left(\frac{-43}{50}\right)^2}\) = \(\sqrt{3.46-(-0.86)^2}\)
= \(\sqrt{3.46-0.7396}=\sqrt{2.7204}\)
∴ S = 1.65 इकाई
विषमतांक j = \(\frac{\bar{X}-M_0}{S}=\frac{21.14-20}{1.65}=\frac{1.14}{1.65}\)
∴ j = 0.69

प्रश्न 9.
एक आवृत्ति वितरण के लिए n = 200, Σf (\(\bar{X}\) – 240) = 0, Σf (x – 240)² = 11250 और मध्यका = 246 हो, तो विषमतांक ज्ञात और उसका प्रकार बताइए ।
उत्तर :
यहाँ Σf (x – 240) = 0 है अर्थात् \(\bar{X}\) = 240 Σf (x – 240)² = 11250 है अर्थात् Σf (x – \(\bar{X}\)) = 11250
∴ S = \(\sqrt{\frac{\Sigma f(X-\bar{X})^2}{n}}\)
= \(\sqrt{\frac{11250}{200}}\)
= \(\sqrt{56.25}\)
∴ S = 7.5

j = \(\frac{3(\bar{X}-M)}{S}\)
= \(\frac{3(240-246)}{7.5}\)
= \(\frac{3(-6)}{7.5}\)
= \(\frac{-18}{7.5}\)
∴ j = – 2.4
आवृत्ति वितरण में ऋण विषमता है ।

विभाग – F

निम्न प्रश्नों के उत्तर दीजिए ।

प्रश्न 1.
निर्धारित समय से अधिक समय ड्राइविंग करने से हुए दुर्घटनाओं की संख्या का आवृत्ति वितरण निम्नानुसार है । उस पर से बाउली की विधि से विषमतांक ज्ञात करो ।

उत्तर :
बाउली की पद्धति में तृतीय चतुर्थक, द्वितीय चतुर्थक और प्रथम चतुर्थक ज्ञात करेंगे । इसके लिए आवृत्ति वितरण को चढ़ते ।
क्रममें गठित करेंगे और संचयी आवृत्ति cf की सारणी बनायेंगे ।

निर्धारित समय से अधिक समय ड्राइविंग घण्टों में	दुर्घटनाओं की संख्या	cf
0	1	1
1.0	2	3
1.5	2	5
2.0	1	6
2.5	2	8
3.0	3	11
3.5	4	15
4.0	5	20

प्रथम चतुर्थक Q₁ = \(\frac{n+1}{4}\) वाँ अवलोकन मूल्य
= \(\frac{20+1}{4}=\frac{21}{4}\) = 5.25 वाँ अवलोकन मूल्य संचयी आवृत्ति वितरण में देखने पर अवलोकन 5.25 का मूल्य 2 है ।
∴ Q₁ = 2 घण्टे
द्वितीय चतुर्थक = माध्यिका = M = \(\frac{\mathrm{n}+1}{2}\) वाँ अवलोकन मूल्य
= \(\frac{20+1}{2}=\frac{21}{2}\) = 10.5 वाँ अवलोकन मूल्य संचयी आवृत्ति की सारणी में देखने पर अवलोकन 10.5 का मूल्य 3 है ।
∴ M = 3 घण्टे
तृतीय चतुर्थक Q₃ = \(\frac{3(n+1)}{4}\) वाँ अवलोकन मूल्य
\(\frac{3(20+1)}{4}=\frac{3 \times 21}{4}\) = 15.75 वाँ अवलोकन मूल्य cf की सारणी में देखने पर 15.75 के अनुरूप अवलोकन का मूल्य 4 है ।
∴ Q₃ = 4 घण्टे
बाउली का विषमतांक j = \(\frac{\mathrm{Q}_3+\mathrm{Q}_1-2 \mathrm{M}}{\mathrm{Q}_3-\mathrm{Q}_1}\)
= \(\frac{4+2-2 \times 3}{4-2}=\frac{6-6}{2}=\frac{0}{2}\)
∴ j = 0

प्रश्न 2.
वर्ष 2015 में एक शहर का तापमान निम्नानुसार दर्ज किया गया है । एक दिन का तापमान – 10° से कम दर्ज नहि हुआ। इस सूचना पर से कार्लपियर्सन की विधि से विषमतांक ज्ञात करो और प्रकार बताइए ।

उत्तर :
मध्यमूल्य दिया है उस पर से मूल आवृत्ति वितरण प्राप्त करके आवृत्ति वितरण में वर्गलम्बाई असमान है । कार्लपियर्सन का विषमतांक ज्ञात करने के लिए माध्य, माध्यिका और प्रमाप विचलन ज्ञात करेंगे ।

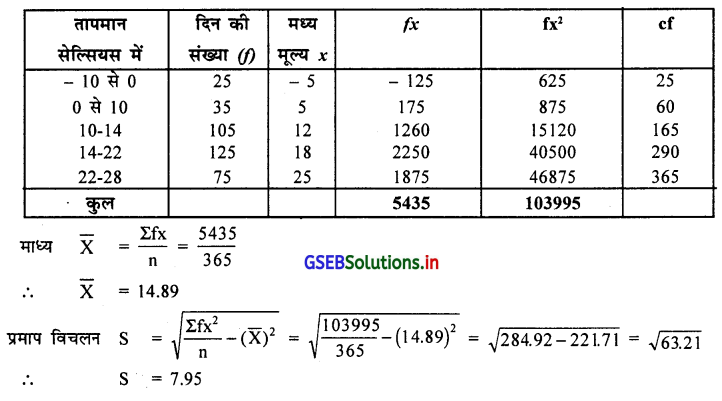
M = \(\frac{n}{2}\) वाँ अवलोकन मूल्य
= \(\frac{365}{2}\)
= 182.5 वाँ अवलोकन मूल्य cf की सारणी में देखने पर 182.5 के अनुरूप M वर्ग = 14 – 22 प्राप्त होगा।
∴ M = L + \(\frac{\frac{n}{2}-c f}{f}\) × c
जहा L = 14, \(\frac{\mathrm{n}}{2}\) = 182.5 cf = 165, f = 125, c = 8
M = 14 + \(\frac{182.5-165}{125}\) × 8
= 14 + 17.5 × 8
= 14 + \(\frac{140}{125}\) = 14 + 1.12
M = 15.12 सेल्सियस
विषमतांक j  = \(\frac{3(\overline{\mathrm{X}}-\mathrm{M})}{\mathrm{S}}=\frac{3(14.89-15.12)}{7.95}\) = \(\frac{3(-0.23)}{7.95}=\frac{-0.69}{7.95}\) = – 0.087
∴ j = – 0.09
आवृत्ति वितरण में ऋण विषमता है ।

प्रश्न 3.
60 नंबर की एक परीक्षा में विद्यार्थियों द्वारा प्राप्त नंबर का आवृत्ति वितरण निम्नानुसार है । कार्लपियर्सन की पद्धति से विषमतांक ज्ञात करो और विषमता का प्रकार बताइए ।

उत्तर :
आवृत्ति वितरण द्वि भूयिष्ठकवाला है इसलिए माध्य, मध्यका और प्रमाप विचलन की गणना करें ।

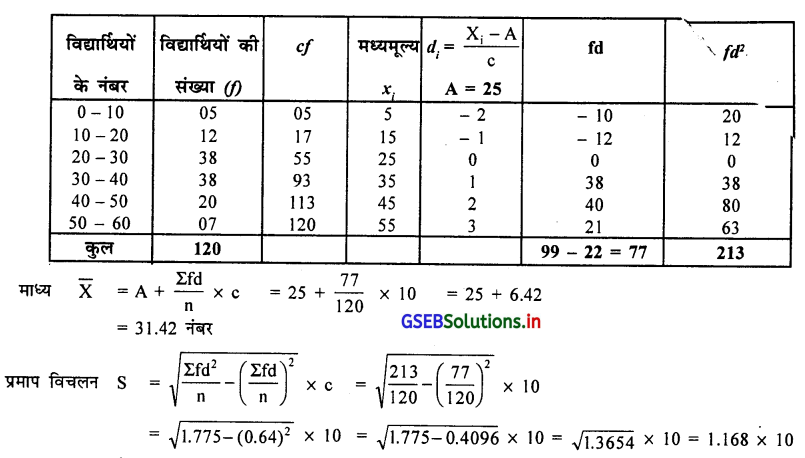
मध्यका M = \(\frac{n}{2}\) वाँ अवलोकन मूल्य
मध्यका M = \(\frac{120}{2}\)
= 60 वाँ अवलोकन मूल्य cf की सारणी में देखने पर M वर्ग 30-40 प्राप्त होगा।
मध्यका M = L + \(\frac{\frac{n}{2}-c f}{f}\) × c
जहा L = 30, \(\frac{\mathrm{n}}{2}\) = 60, cf = 55, f = 38, c = 10
= 30 + \(\frac{60-55}{38}\) × 10 = 30 + \(\frac{50}{38}\) = 30 + 1.32
∴ M = 31.32 नंबर
j = \(\frac{3(\overline{\mathrm{X}}-\mathrm{M})}{\mathrm{S}}=\frac{3(31.42-31.32)}{11.68}\) = \(\frac{3(0.1)}{11.68}=\frac{0.3}{11.68}\)
∴ j = 0.026
आवृत्ति वितरण संमितता के समीप है ।

प्रश्न 4.
वर्ष 2015-16 में 150 कंपनियाँ द्वारा किया गया लाभ का निम्न आवृत्ति वितरण पर से योग्य पद्धति से विषमतांक ज्ञात करो और विषमता का प्रकार बताइए ।

उत्तर :
आवृत्ति वितरण खुल्ले शिरावाला है इसलिए बाउली की पद्धति से विषमतांक ज्ञात करेंगे इसके लिए Q₃ M, Q₁ ज्ञात करेंगे ।

लाभ (लाख रु.)	कंपनीयों की संख्या	cf
10 से कम	15	15
10-20	30	45
20 -30	50	95
30-40	40	135
40 से अधिक	15	150
कुल	150

प्रथन चतुर्थक Q₁ = \(\frac{n}{4}\) वाँ अवलोकन मूल्य
= \(\frac{150}{4}\) = 37.5 वाँ अवलोकन मूल्य cf की सारणी में देखने पर 37.5 के अनुरूप वर्ग 10 – 20 होगा ।
∴ Q₁ वर्ग = 10-20
∴ Q₁ = L + \(\frac{\frac{n}{4}-c f}{f}\) × c
जहा L = 10, \(\frac{n}{4}\) = 37.5, cf = 15, f = 30, c = 10
Q₁ = 10 + \(\frac{37.5-15}{30}\) × 10 = 10 + \(\frac{22.5 \times 10}{30}\) = 10 + 7.5
∴ Q₁ = 17.5 लाख रु.
तृतीय चतुर्थक Q₃ = 3(\(\frac{\mathrm{n}}{4}\)) वाँ अवलोकन मूल्य
= \(\frac{3 \times 150}{4}\)
= 112.5 वाँ अवलोकन मूल्य cf की सारणी में देखने पर Q₃ वर्ग 30 – 40 प्राप्त होगा ।
Q₃ = L + \(\frac{3\left(\frac{n}{4}\right)-c f}{f}\) × c
जहाँ L = 30, 3 (\(\frac{n}{4}\)) = 112.5, cf = 95, f = 40, c = 10
Q₃ = 30 + \(\frac{112.5-95}{40}\) × 10 30 + \(\frac{17.5 \times 10}{40}\) = 30 + 4.375
∴ Q₃ = 34.38 लाख रु.
मध्यका M = \(\frac{\mathrm{n}}{2}\) वाँ अवलोकन मूल्य
= \(\frac{150}{2}\)
= 75 वाँ अवलोकन मूल्य cf की सारणी में देखने पर M वर्ग 20 – 30 प्राप्त होगा ।

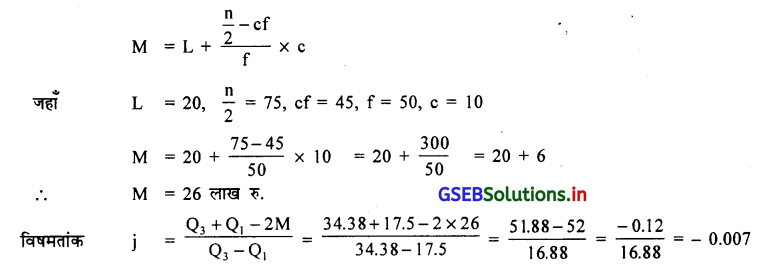
आवृत्ति वितरण में ऋण विषमता है ।

प्रश्न 5.
किसी एक वस्तु की माँग का आवृत्ति वितरण निम्नानुसार है । उस पर से कार्लपियर्सन की पद्धति से विषमता और विषमतांक ज्ञात करो ।

उत्तर :
आवृत्ति वितरण मिश्र प्रकार का है इसलिए माध्य, मध्यका और प्रमाप विचलन की गणना करेंगे ।

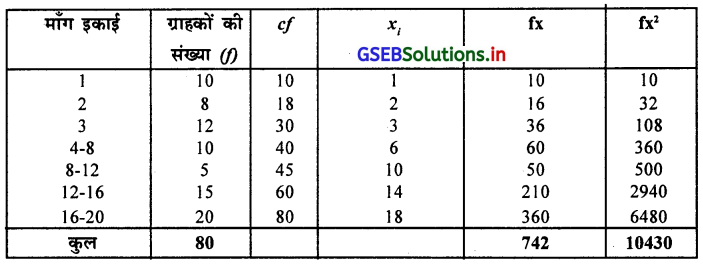
माध्य \(\frac{\Sigma \mathrm{fx}}{\mathrm{n}}=\frac{742}{80}\) = 9.275
∴ \(\bar{X}\) = 9.28 इकाई
प्रमाप विचलन S = \(\sqrt{\frac{\Sigma \mathrm{fx}^2}{\mathrm{n}}-(\overline{\mathrm{X}})^2}\) = \(\sqrt{\frac{10430}{80}-(9.28)^2}\)
= \(\sqrt{130.375-86.118}=\sqrt{44.257}\)
∴ S = 6.65 इकाई
मध्यका M = \(\frac{\mathrm{n}}{2}\) वाँ अवलोकन मूल्य
= \(\frac{80}{2}\)
= 40 वाँ अवलोकन मूल्य cf की सारणी में देखने पर मध्यका वर्ग 4-8 प्राप्त होगा ।
∴ M = L + \(\frac{\frac{\mathrm{n}}{2}-\mathrm{cf}}{\mathrm{f}}\) × c
जहाँ L = 4, \(\frac{\mathrm{n}}{2}\) = 40, cf = 30, f = 10, c = 4
M = 4 + \(\frac{40-30}{10}\) × 4 = 4 + \(\frac{40}{10}\) = 4 + 4
∴ M = 8 इकाई
विषमतांक j = \(\frac{3(\overline{\mathrm{X}}-\mathrm{M})}{\mathrm{S}}=\frac{3(9.28-8)}{6.65}\) = \(\frac{3 \times 1.28}{6.65}=\frac{3.84}{6.65}\)
∴ j = 0.58
विषमता SK = 3 (\(\overline{\mathrm{X}}\) – M) = 3 (9.28 – 8) = 3 × 1.28
∴ SK = 3.84

प्रश्न 6.
निम्न आवृत्ति वितरण एक कारखाना में उत्पादित हुए स्क्रू का है । उस पर से बाउली की पद्धति से विषमतांक ज्ञात करो और अर्थघटन करो ।

उत्तर :
आवृत्ति वितरण ‘से कम’ प्रकार है इसलिए मूल आवृत्ति वितरण ज्ञात करके Q₁, Q₂ = M, Q₃ ज्ञात करेंगे ।

स्क्रू के व्यास का माप (मि.मि.)	स्क्रू की संख्या (f)	cf
4 – 4.1	06	6
4.1 – 4.2	07	13
4.2 – 4.3	10	23
4.3 – 4.4	10	33
4.4 – 4.5	08	41
4.5 – 4.6	05	46
4.6 – 4.7	02	48
4.7 – 4.8	02	50

प्रथम चतुर्थक Q₁ = \(\frac{n}{4}\) वा अवलोकन मूल्य
= \(\frac{50}{4}\) = 12.5 वाँ अवलोकन मूल्य of की सारणी में देखने पर Q₁ वर्ग 4.1 से 4.2 प्राप्त होगा ।
∴ Q₁ = L + \(\frac{\frac{n}{4}-c f}{f}\) × C
जहाँ L = 4.1, \(\frac{n}{4}\) = 12.5, cf = 6, = 07, c = 0.1
Q₁ = 4.1 + \(\frac{12.5-6}{7}\) × 0.1 = 4.1 + \(\frac{6.5 \times 0.1}{7}\) + 0.09
∴ Q₁ = 4.19 मि.मि.
मध्यका M = \(\frac{\mathrm{n}}{2}\) वाँ अवलोकन मूल्य M = \(\frac{50}{2}\) = 25 cf की सारणी मे देखने पर M वर्ग 4.3 – 4.4
M = L + \(\frac{\frac{n}{2}-c f}{f}\) × c
जहाँ L = 4.3, \(\frac{n}{2}\) = 25, cf = 23, f = 10, c = 0.1
M = 4.3 +\(\frac{25-23}{10}\) × 0.1 = 4.3 + \(\frac{2 \times 0.1}{10}\) = 4.3 + 0.02
∴ M = 4.32 मि.मि.
तृतीय चतुर्थक Q₃ = 3 (\(\frac{\mathrm{n}}{4}\)) वाँ अवलोकन मूल्य
= \(\frac{3 \times 50}{4}\) = 3 × 12.5
= 37.5 वाँ अवलोकन मूल्य cf की सारणी में देखने पर Q₃ वर्ग 4.4 से 4.5 प्राप्त होगा ।
Q₃ L + \(\frac{3\left(\frac{n}{4}\right)-c f}{f}\) × C
जहाँ L = 4.4, 3(\(\frac{n}{4}\)) = 37.5, cf = 33, f = 8, c = 0.1
Q₃ = 4.4 + \(\frac{37.5-33}{8}\) × 0.1 = 4.4 + \(\frac{4.5 \times 0.1}{8}\) = 4.4 + 0.06
∴ Q₃ = 4.46 मि.मि.

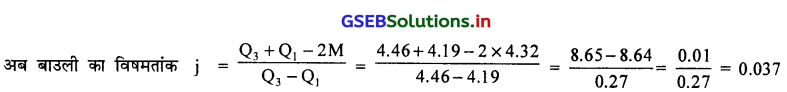
आवृत्ति वितरण में विषमतांक का मूल्य 0.037 प्राप्त हुआ है जो संमितता के अधिक समीप है ।

प्रश्न 7.
एक डिपार्टमेन्ट स्टोर्स में एक दिन ब्रेड के पेकेट की बिक्री का आवृत्ति वितरण पर से कार्लपियर्सन की पद्धति से विषमतांक ज्ञात करके अर्थघटन करो ।

उत्तर :
आवृत्ति वितरण में वर्गलम्बाई असमान है इसलिए माध्य, मध्यका और प्रमाप विचलन ज्ञात करेंगे ।

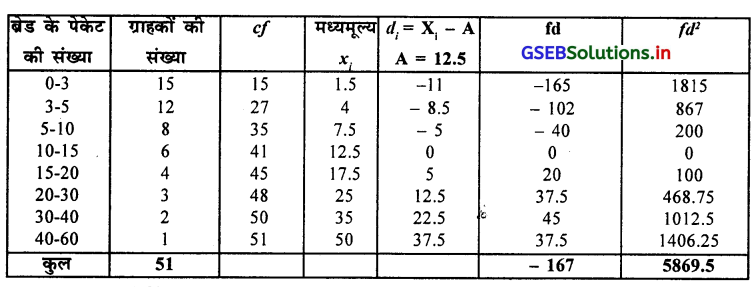
माध्य \(\overline{\mathrm{x}}\) A + \(\frac{\Sigma \mathrm{fd}}{n}\) = 12.5 – \(\frac{167}{51}\) = 12.5 – 3.27
= 9.23 पेकेट
मध्यका M = \(\frac{n}{2}\) वाँ अवलोकन मूल्य
= \(\frac{51}{2}\)
= 25.5 वाँ अवलोकन मूल्य cf की सारणी में देखने पर M वर्ग 3-5 . .
M = L + \(\frac{\frac{n}{2}-c f}{f}\) x c
जहाँ L = 3, \(\frac{n}{2}\) = 25.5, cf = 15, f = 12, c = 2
M = 3 + \(\frac{25.5-15}{12}\) x 2 = 3 + \(\frac{10.5 \times 2}{12}\) = 3 + 1.75
∴ M = 4.75 पेकेट

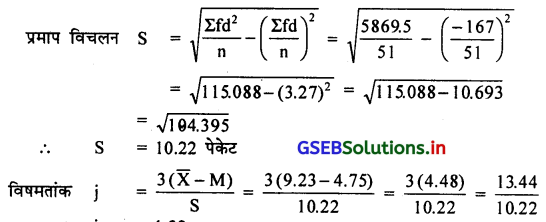
j = 1.32
भूयिष्ठक के स्थान पर मध्यका का उपयोग करने से विषमतांक का मूल्य – 3 से + 3 के बीच आ सकता है ।

प्रश्न 8.
काँच की बिक्री करनेवाली एक दुकान में बिक्री का आवृत्ति वितरण निम्नानुसार है । बाउली की पद्धति से विषमतांक ज्ञात करो और उसका अर्थघटन करो ।

उत्तर :
बाउली का विषमतांक ज्ञात करने के लिए Q₃, Q₂, Q₁ ज्ञात करेंगे ।

कांच का कद (चो.मी.मी.)	ग्राहकों की संख्या	cf
1 – 1.9	10	10
2 – 2.9	40	50
3 – 3.9	20	70
4 – 4.9	50	120
5 – 5.9	30	150
6 – 6.9	30	180
7 – 7.9	20	200

प्रथम चतुर्थक Q₁ = \(\frac{n}{4}\) वाँ अवलोकन मूल्य
= \(\frac{200}{4}\) = 50 वाँ अवलोकन मूल्य cf की सारणी में देखने पर Q₁ वर्ग 2-2.9 प्राप्त होगा । वर्ग अनिवारक है इसलिए सीमाबिंदु ज्ञात करने पर 1.95 – 2.95 प्राप्त होगा ।
∴ Q₁ = L + \(\frac{\frac{n}{4}-c f}{f}\) × c
जहाँ L = 1.95, \(\frac{n}{4}\) = 50, cf = 10, f = 40, c = 1
Q₁ = 1.95 + \(\frac{50-10}{40}\) × 1 = 1.95 + 1
∴ Q₁ = 2.95 चो.मी.
मध्यका M = \(\frac{\mathrm{n}}{2}\) वाँ अवलोकन मूल्य
= \(\frac{200}{2}\) = 100 वाँ अवलोकन मूल्य cf की सारणी में देखने पर M वर्ग 4 – 4.9 प्राप्त होगा। वर्ग अनिवारक है इसलिए सीमाबिंदु प्राप्त करने पर 3.95 – 4.95 वर्ग प्राप्त होगा ।
M = L + \(\frac{\frac{n}{2}-c f}{f}\) × C = 3.95 + \(\frac{100-70}{50}\) × 1 = 3.95 + \(\frac{30}{50}\) + 0.6
∴ M = 4.55 चो.मी.
तृतीय चतुर्थक Q₃ = 3 (\(\frac{n}{4}\)) वाँ अवलोकन मूल्य
= \(\frac{3 \times 200}{4}\)
= 150 वाँ अवलोकन मूल्य cf की सारणी में देखने पर Q₃ वर्ग = 5-5.9 प्राप्त होगा। वर्ग अनिवारक प्रकार का है इसलिए सीमाबिंदु प्राप्त करने पर 4.95 – 5.95 प्राप्त होगा ।
Q₃ = L + \(\frac{3\left(\frac{n}{4}\right)-c f}{f}\) × c
जहाँ L = 4.95, 3(\(\frac{n}{4}\)) = 150, cf = 120, f = 30, c = 1

⇒ आवृत्ति वितरण में ऋण विषमता है।

प्रश्न 9.
एक कन्स्ट्रक्शन कंपनी द्वारा भिन्न-भिन्न क्षेत्रफलवाले मकान तैयार किये है । उसका आवृत्ति वितरण निम्नानुसार है ।

उत्तर :
आवृत्ति वितरण में एक भूयिष्ठक है इसलिए \(\bar{x}\), M_O, S ज्ञात करेंगे ।

मकान का क्षेत्रफल (चो.मी.)	मकानों की संख्या f	fx	fx2
100	10	1000	100000
140	25	3500	490000
180	50	9000	1620000
220	25	5500	1210000
260	10	2600	676000
कुल	120	fx	4096000

माध्य \(\overline{\mathrm{X}}=\frac{\Sigma \mathrm{fx}}{\mathrm{n}}=\frac{21600}{120}\)
\(\bar{X}\) = 180 चो.मी. क्षेत्रफल
भूयिष्ठक महत्तम आवृत्ति 50 के अनुरूप अवलोकन 180 है ।
∴ M_O = 180 चो.मी. क्षेत्रफल
प्रमाप विचलन S = \(\sqrt{\frac{\Sigma \mathrm{fx}^2}{\mathrm{n}}-(\overline{\mathrm{X}})^2}=\sqrt{\frac{4096000}{120}-(180)^2}\) = \(\sqrt{3413333-32400}=\sqrt{173333}\)
S = 41.63 चो.मी. क्षेत्रफल
विषमतांक j = \(\frac{\overline{\mathrm{X}}-\mathrm{M}_0}{\mathrm{~S}}=\frac{180-180}{41.63}=\frac{0}{41.63}\)
j = 0
आवृत्ति वितरण सममितिय है ।

प्रश्न 10.
फैक्टरी में उत्पादन के दौरान एक घण्टे में भिन्न-भिन्न मशीन में उपयोग में लिए गए पावर युनिट का आवृत्ति वितरण पर से बाउली की विधि से विषमतांक ज्ञात करो ।

उत्तर :
बाउली का विषमतांक ज्ञात करने के लिए Q₃, Q₁, M ज्ञात करेंगे ।

उपयोग में लिए गए युनिट	यंत्रों की संख्या f	cf
10 – 15	5	5
15 – 20	10	15
20 – 25	15	30
25 – 30	20	50
30 – 35	25	75
35 – 40	30	105
कुल	105

मध्यका M = \(\frac{n}{2}\) वाँ अवलोकन मूल्य
M = \(\frac{105}{2}\) = 52.5 वाँ अवलोकन मूल्य cf की सारणी में देखने पर M वर्ग 30 – 35
∴ M = L + \(\frac{\frac{n}{2}-c f}{f}\) × c
जहाँ L = 30, \(\frac{\mathrm{n}}{2}\) = 52.5, cf = 50, f = 25, c = 5
30 + \(\frac{52.5-50}{25}\) × 5 = 30 + \(\frac{2.5 \times 5}{25}\) = 30 + 0.5
∴ M = 30.5
प्रथम चतुर्थक Q₁ = \(\frac{n}{4}\) वाँ अवलोकन मूल्य
= \(\frac{105}{4}\) = 26.25 वाँ अवलोकन मूल्य cf की सारणी में देखने पर 26.25 के अनुरूप Q₁ वर्ग = 20-25
Q₁ = L + \(\frac{\frac{n}{4}-\mathrm{cf}}{\mathrm{f}}\) × c
जहाँ L = 20, \(\frac{n}{4}\) = 26.25, cf = 15, f = 15, c = 5
∴ Q₁ = 20 + \(\frac{26.25-15}{15}\) × 5 = 20 + \(\frac{11.25 \times 5}{15}\) = 20 + 3.75
Q₁ = 23.75
तृतीय चतुर्थक Q₃ = 3 (\(\frac{\mathrm{n}}{4}\)) वाँ अवलोकन मूल्य
= \(\frac{3 \times 105}{4}\) = 3 × 26.25
= 78.75 वाँ अवलोकन मूल्य cf की सारणी में देखने पर Q₃ वर्ग = 35-40

विषमता के सूत्र (Formulae)

(1) कार्लपियर्सन की पद्धति (Method of Karl Pearson) :
विषमता SK = \(\bar{x}\) – M_O
विषमतांक j = \(\frac{\bar{X}-M_0}{S}\)

अथवा
यदि भूयिष्ठक प्राप्त नहीं हो सकता तब इस सूत्र का उपयोग करते है ।
विषमता SK = 3 (\(\bar{X}\) – M)
विषमतांक j = \(\frac{3(\overline{\mathrm{X}}-\mathrm{M})}{\mathrm{S}}\)

(2) बाउली की विधि (Bowley’s Method) :
विषमता SK = (Q₃ – M) – (M – Q₁)
अथवा
Q₃ + Q₁ – 2M
विषमता j = \(\frac{\left(Q_3-M\right)-\left(M-Q_1\right)}{\left(Q_3-M\right)+\left(M-Q_1\right)}\)
अथवा
j = \(\frac{\mathrm{Q}_3+\mathrm{Q}_1-2 \mathrm{M}}{\mathrm{Q}_3-\mathrm{Q}_1}\)