GSEB Solutions Class 11 Statistics Chapter 9 गुणोत्तर श्रृंखला Ex 9

Gujarat Board Statistics Class 11 GSEB Solutions Chapter 9 गुणोत्तर श्रृंखला Ex 9 Textbook Exercise Questions and Answers.

Gujarat Board Textbook Solutions Class 11 Statistics Chapter 9 गुणोत्तर श्रृंखला Ex 9

विभाग – A

निम्न विकल्प में से सहि विकल्प पसंद करके लिखो ।

प्रश्न 1.
गुणोत्तर-श्रेणी 0.2, 1, 5 ……………. का छठ्ठा पद बताइए ।
(A) 25
(B) 0.25
(C) 0.1
(D) 625
उत्तर :
(D) 625

प्रश्न 2.
एक गुणोत्तर-श्रेणी का प्रथमपद a और सामान्य गुणोत्तर b है तो (n + 1) वाँ पद बताइए ।
(A) abⁿ
(B) arⁿ
(C) ab^{n – 1}
(D) ar^{n – 1}
उत्तर :
(A) abⁿ

प्रश्न 3.
गुणोत्तर-श्रेणी 1, √3, 3, 3√3………. का पाँचवा पद ज्ञात करो ।
(A) 9
(B) 9√3
(C) 27
(D) \(\frac{(\sqrt{3})^5-1}{(\sqrt{3}-1)}\)
उत्तर :
(A) 9

प्रश्न 4.
एक गुणोत्तर-श्रेणी में T₁ = a और T₅ = \(\frac{1}{a}\) जहाँ a > 0 हो, तो तीसरा पद ज्ञात करो ।
(A) a²
(B) 1
(C) = \(\frac{1}{\mathrm{a}^2}\)
(D) a
उत्तर :
(B) 1

प्रश्न 5.
गुणोत्तर-श्रेणी \(\frac{1}{9}\), \(\frac{1}{3}\), 1 का सातवा पद ज्ञात करो ।
(A) 6561
(B) 243
(C) 81
(D) \(\frac{1}{81}\)
उत्तर :
(C) 81

प्रश्न 6.
एक गुणोत्तर-श्रेणी का n वा पद 3(2n – 1) हो, तो सामान्य अनुपात ज्ञात करो ।
(A) 3
(B) 2
(C) 6
(D) 1
उत्तर :
(B) 2

प्रश्न 7.
गुणोत्तर-श्रेणी 0.4, 0.04, 0.004……… का सामान्य अनुपात बताइए ।
(A) 10
(B) 0.4
(C) 4
(D) 0.1
उत्तर :
(D) 0.1

प्रश्न 8.
यदि x, 10, – 25 गुणोत्तर-श्रेणी में हो तो x का मूल्य ज्ञात करो ।
(A) 4
(B) – 25
(C) – 4
(D) 2
उत्तर :
(C) – 4

प्रश्न 9.
यदि गुणोत्तर-श्रेणी का सामान्य गुणोत्तर-1 और प्रथमपद 1 हो, तो प्रथम 6 पदों का योग ज्ञात करो ।
(A) 0
(B) -1
(C) 1
(D) 6
उत्तर :
(A) 0

प्रश्न 10.
यदि गुणोत्तर-श्रेणी का सामान्य गुणोत्तर 1 हो और S₁₀ = 40 हो, तो प्रथमपद ज्ञात करो ।
(A) 0
(B) 10
(C) 4
(D) 400
उत्तर :
(C) 4

विभाग – B

निम्न प्रश्नों के उत्तर एक वाक्य में लिखिए ।

प्रश्न 1.
गुणोत्तर-श्रेणी ar, ar², ar³…… का n वाँ पद क्या होगा ?
उत्तर :
गुणोत्तर-श्रेणी ar, ar², ar³….. का n वा पद ar” होगा ।

प्रश्न 2.
गुणोत्तर-श्रेणी 0.1, 0.01, 0.001…. का सामान्य गुणोत्तर ज्ञात करो ।
उत्तर :
यहाँ T₁ = 0.1 : T₂ = 0.01
∴ r = \(\frac{\mathrm{T}_2}{\mathrm{~T}_1}=\frac{0.01}{0.1}\) = 0.1
सामान्य अनुपात r = 0.1 होगा ।

प्रश्न 3.
गुणोत्तर-श्रेणी 7, 7, 7…. के लिए प्रथम 20 पदों का योग ज्ञात करो।
उत्तर :
यहाँ a = 7 सामान्य अनुपात r = \(\frac {7}{7}\) = 1 है ।
प्रथम 20 पदों का योग ज्ञात करना है । ∴ n = 20 ∴ r = 1 है ।
S_n = n_a
∴ S₂₀ = 20 × 7
∴ S₂₀ = 140 प्रथम 20 पदों का योग 140 होगा ।

प्रश्न 4.
यदि गुणोत्तर-श्रेणी का n वाँ पद T_n = 2^{n + 1} हो, तो सामान्य गुणोत्तर ज्ञात करो ।
उत्तर :
T_n = 2^{n + 1} दिया है ।

∴ T₁ = 2^{1 + 1}
= 2²
∴ T₁ = 4

∴ T₂ = 2^{2 + 1}
T₂ = 2³
∴ T₂ = 4

अब r = \(\frac{T_2}{T_1}\)
= \(\frac{4}{2}\)
= 2
∴ सामान्य अनुपात 2 होगा ।

प्रश्न 5.
यदि संख्याएँ 4, 1, y गुणोत्तर-श्रेणी में हो, तो y का मूल्य ज्ञात करो ।
उत्तर :
यहाँ T₁ = 4, T₂ = 1, T₃ = y है ।
सामान्य अनुपात = \(\frac{T_2}{T_1}=\frac{T_3}{T_2}\)
∴ = \(\frac{1}{4}=\frac{y}{1}\)
∴ 4y = 1
∴ y = \(\frac{1}{4}\)
y का मूल्य = \(\frac{1}{4}\) होगा ।

प्रश्न 6.
एक गुणोत्तर-श्रेणी में किसी भी दो क्रमिक पदों का योग शून्य हो तो सामान्य गुणोत्तर क्या होगा ?
उत्तर :
क्रमिक पदों का योग शून्य होता है अर्थात् एक संख्या ऋण और एक संख्या धन होगी दोनों संख्या समान होगी इसलिए सामान्य अनुपात = – 1 होगा ।
उदा. : एक संख्या – 5 है तो दूसरी संख्या 5 होगी ।
∴ r = \(\frac{5}{-5}\) = – 1

प्रश्न 7.
एक गुणोत्तर-श्रेणी में S₆ = 15 और S₅ = 11 हो, तो छठा पद ज्ञात करो ।
उत्तर :
T_{N + 1} = S_{n + 1} – S_n
T_{5 + 1} = S_{5 + 1} – S₅
T₆ = S₆ – S₅
∴ T₆ = 15 – 11
∴ T₆ = 4
∴ छठ्ठा पद 4 होगा ।

प्रश्न 8.
विधान “यदि a, b, c, d गुणोत्तर-श्रेणी में हो, तो ad = bc होगा” सत्य है या असत्य ?
उत्तर :
a, b, c, d गुणोत्तर-श्रेणी में है ।
∴ \(\frac{\mathrm{b}}{\mathrm{a}}=\frac{\mathrm{c}}{\mathrm{b}}=\frac{\mathrm{d}}{\mathrm{c}}\) = r होगा ।
∴ \(\frac{\mathrm{b}}{\mathrm{a}}=\frac{\mathrm{d}}{\mathrm{c}}\) होगा ।
∴ bc = ad
∴ ad = bc
विधान सत्य है ।

प्रश्न 9.
गुणोत्तर-श्रेणी के लिए विधान “T₁ = S₁” सत्य है या असत्य बताइए ।
उत्तर :
T₁ = प्रथम पद होता है ।
S₁ = प्रथम पद होता है ।
इसलिए T₁ = S₁ विधान सत्य है ।

विभाग – C

निम्न प्रश्नों के उत्तर दीजिए ।

प्रश्न 1.
गुणोत्तर-श्रेणी की परिभाषा दीजिए ।
उत्तर :
यदि a और r शून्येतर वास्तविक संख्याएँ हो तो धनपूर्णांक n ≥ 1 के लिए श्रृंखला का n वा पद T_n = ar^{n – 1} हो तो ऐसी श्रृंखला को गुणोत्तर-श्रेणी कहते है । a यह श्रृंखला का प्रथमपद और यह श्रृंखला का सामान्य गुणोत्तर (Common Ratio) कहा जाता है। श्रृंखला का सामान्य गुणोत्तर समान होने से गुणोत्तर-श्रेणी को समानुपातिक श्रृंखला भी कहते है ।

प्रश्न 2.
आनुपातिक श्रेढ़ी की परिभाषा दीजिए।
उत्तर :
यदि सभी पदों a और r के स्वरूप में प्रदर्शित करे, तो S_n = a + ar + ar² + ….. + ar^{n – 1} S_n को आनुपातिक श्रेढी (Geometric Series) कहा जाता है ।

प्रश्न 3.
एक गुणोत्तर-श्रेणी में सामान्य गुणोत्तर 1 हो और S₈ = 24 हो तो प्रथमपद ज्ञात करो।
उत्तर :
यहाँ सामान्य अनुपात r = 1 और S₈ = 24 दिया है । प्रथमपद = a ज्ञात करना है ।
r = 1 है । ∴ S_n = na होगा
∴ S₈ = 8 × a
∴ 24 = 8 × a
∴ a = \(\frac{24}{8}\)
∴ a = 3
इसलिए प्रथमपद 3 होगा ।

प्रश्न 4.
गुणोत्तर-श्रेणी में T₁ = 2 और प्रथम तीन पदों का गुणाकार 1000 हो, तो सामान्य गुणोत्तर ज्ञात करो ।
उत्तर :
यहाँ T₁ = 2 है ∴ प्रथमपद a = 2 होगा ।
तीन पदों का गुणाकार 1000 है ।
∴ प्रथम तीन पद T₁, T₂, T₃ होगा T₁ = a, T₂, ar, T₃ = ar²

∴ T₁ × T₂ × T₃ = 1000
∴ a × ar × ar² = 1000
∴ a³r³ = 1000
∴ (ar)³ = (10)³
∴ ar = 10 a = 2 रखने पर
∴ 2 × r = 10
∴ r = \(\frac{10}{2}\)
∴ r = 5
सामान्य अनुपात 5 होगा ।

प्रश्न 5.
यदि गुणोत्तर श्रृंखला में a = 2 और r = 3 हो, तो प्रथम 4 पदों का योग ज्ञात करो ।
उत्तर :
यहाँ a = 2, सामान्य गुणोत्तर r = 3 दिया है । प्रथम 4 पदों का योग ज्ञात करना है । ∴ n = 4
सामान्य गुणोत्तर = 3 r > 1 दिया है ।
इसलिए S_n = \(\frac{a\left(r^n-1\right)}{r-1}\)
∴ S₄ = \(\frac{2\left(3^4-1\right)}{3-1}\)
∴ S₄ = \(\frac{2(81-1)}{2}\)
∴ S₄ = \(\frac{2 \times 80}{2}\)
∴ S₄ = 80
इसलिए प्रथम चार पदों का योग 80 होगा ।

प्रश्न 6.
गुणोत्तर-श्रेणी 4, 12, 36….. का कौन-सा पद 324 होगा ?
उत्तर :
यहाँ a = 4 और सामान्य गुणोत्तर r = \(\frac{T_2}{T_1}\)
∴ r = \(\frac{12}{4}\)
∴ r = 3

अब T_n = 324
∴ T_n = ar^{n – 1} में a = 4, r = 3, T_n = 324 रखने पर
∴ 324 = 4 × 3^{n – 1}
∴ \(\frac{324}{4}\) = 3^{n – 1}
∴ 81 = 30 – 1
∴ 3⁴ = 3^{n – 1} दोनों ओर घात की तुलना करने पर
∴ n – 1 = 4
∴ n = 4 + 1
∴ n = 5
इसलिए श्रृंखला का 5 वाँ पद 324 होगा ।

प्रश्न 7.
एक गुणोत्तर-श्रेणी a = \(\frac {4}{9}\) और r = \(\frac{-3}{2}\) हो तो T₃ = ……
उत्तर :
यहाँ a = \(\frac {4}{9}\) और r = \(\frac{-3}{2}\) दिया है T₃ ज्ञात करना है । ∴ n = 3
यहाँ T_n = ar^{n – 1} का उपयोग करेंगे ।
∴ T₃ = \(\frac {4}{9}\) × (\(\frac{-3}{2}\))^{3 – 1}
∴ = \(\frac {4}{9}\) × (\(\frac{-3}{2}\))²
= \(\frac {4}{9}\) × \(\frac {9}{4}\)
इसलिए T₃ = 1 होगा।

प्रश्न 8.
यदि गुणोत्तर-श्रेणी का सामान्य अनुपात 2 हो तो सातवाँ और तीसरा पद का अनुपात ज्ञात करो ।
उत्तर :
यहाँ सामान्य अनुपात = r = 2 T₇ और T₃ का अनुपात ज्ञात करना है ।
∴ T_n = ar^{n – 1}
∴ T₇ = a × 2^{7 – 1}
= a × 2⁶
= a × 64
∴ T₇ = 64a
∴ T₃ = a × 2^{3 – 1}
T₃ = a × 2²
∴ T₃ = 49

T₇ और T₃ का अनुपात
T₇ = 64a : T₃ : 49
∴ \(\frac{T_7}{T_3}=\frac{649}{49}\)
∴ \(\frac{\mathrm{T}_7}{\mathrm{~T}_3}=\frac{16}{1}\)
∴ T₇ और T₃ का अनुपात 16 : 1 होगा ।

प्रश्न 9.
निम्न श्रृंखला के पद श्रृंखला सूत्र से प्राप्त करो ।
उत्तर :
(1) 2, 10, 50 …. (छठ्ठा पद)
यहाँ a = 2, r = \(\frac {10}{2}\) = 5 और n = 6
T_n = ar^{n – 1} में a = 2, r = 5 और n = 6 रखने पर
T₆ = 2 × 5^{6 – 1}
= 2 × 5⁵
= 2 × 3125
T₆ = 6250

(2) 100, 50, 25…. (सातवाँ पद)
यहाँ प्रथम पद a = 100, सामान्य अनुपात r = \(\frac {50}{100}\) = \(\frac {1}{2}\) और T₇ ज्ञात करना है । ∴ n = 7
T_n = ar^{n – 1} में a = 100, r = \(\frac {1}{2}\) और n = 7 रखने पर
T₇ = 100 × (\(\frac {1}{2}\))^{7 – 1}
= 100 × \(\frac {1}{64}\)
= \(\frac {100}{64}\)
T₇ = \(\frac {25}{16}\)
इसलिए सातवाँ पद T₇ = \(\frac {25}{16}\) होगा ।

(3) \(\frac {1}{3}\), \(\frac {2}{9}\), \(\frac {4}{27}\) ….. (आठवा पद)

इसलिए आठवाँ पद \(\frac{128}{6561}\) होगा ।

(4) 2, 2√2, 4 …. (पाँचवाँ पद)
यहाँ प्रथम पद a = 2, सामान्य अनुपात r = \(\frac{T_2}{T_1}=\frac{2 \sqrt{2}}{2}\) ∴ r = √2 T₅ ज्ञात करना है । ∴ n = 5
T_n = ar^{n – 1} में a = 2, r = √2, n = 5 रखने पर
T₅ = 2 × (√2)^{5 – 1}
= 2 × (√2)⁴
= 2 × 4
T₅ = 8
इसलिए पाँचवा पद 8 होगा ।

विभाग – D

निम्न के हल प्राप्त करो ।

प्रश्न 1.
T₅ 405 और T₇ = 3645 हो तो T₄ ज्ञात करो ।
उत्तर :
मानाकि गुणोत्तर-श्रेणी का प्रथमपद = a और सामान्य गुणोत्तर = r है ।
T₅ = 405 और T₇ = 3645 दिया है ।
इसलिए \(\frac{\mathrm{T}_7}{\mathrm{~T}_5}=\frac{\mathrm{ar}^6}{\mathrm{ar}^4}\) = r²
\(\frac{\mathrm{ar}^6}{\mathrm{ar}^4}=\frac{3645}{405}\)
∴ r² = 9
∴ r = ± 3
अब r = ± 3 को T₅ = ar⁴ = 405 में रखने पर
∴ a × (± 3)⁴ = 405
∴ a × 81 = 405
∴ a = \(\frac{405}{81}\)
∴ a = 5
श्रृंखला का 4 पद ज्ञात करना है यहा n = 4, a = 5, r = ± 3 का मूल्य
T_n = ar^{n – 1} में रखने पर
T₄ = 5 × (± 3)^{4 – 1}
= 5 × (± 3)3 = 5 × ± 27
T₄ = ± 135
श्रृंखला का 4 पद – 135 अथवा 135 होगा ।

प्रश्न 2.
यदि गुणोत्तर-श्रेणी का प्रथमपद \(\frac {27}{16}\) और सामान्य गुणोत्तर \(\frac {2}{3}\) हो, तो T₅ और S₄ ज्ञात करो ।
यहाँ प्रथमपद a = \(\frac {27}{16}\) और सामान्य गुणोत्तर r = \(\frac {2}{3}\) है, T₅ ज्ञात करना है । ∴ n = 5

प्रश्न 3.
दी गई गुणोत्तर-श्रेणी में a = 4 और T₅ = \(\frac {1}{4}\) हो, तो T₇ ज्ञात करो ।
उत्तर :
प्रथमपद a = 4, T₅ = \(\frac {1}{4}\) दिया है ।
T₅ = ar⁴
\(\frac {1}{4}\) = 4 × r⁴
∴ \(\frac {1}{4}\) × \(\frac {1}{4}\) = r⁴
∴ r⁴ = \(\frac {1}{16}\)
∴ r⁴ = (\(\frac {1}{2}\))⁴
∴ r = \(\frac {1}{2}\)

T₇ ज्ञात करना है ।
∴ T_n = ar^{n – 1} में a = 4, r = \(\frac {1}{2}\), n = 7 रखने पर
T₇ = 4 × (\(\frac {1}{2}\))^{7 – 1}
= 4 × (\(\frac {1}{2}\))⁶
= 4 × \(\frac {1}{64}\)
= \(\frac {4}{64}\)
T₇ = \(\frac {1}{16}\)
इसलिए T₇ = \(\frac {1}{16}\) होगा ।

प्रश्न 4.
दी गई गुणोत्तर-श्रेणी में T₂ = 9 और T₅ = 243 हो, तो S₄ ज्ञात करो ।
उत्तर :
T_n = a.r^{n – 1}
∴ T₂ = a.r^{2 – 1}
∴ 9 = a.r ……………. (i)
T₅ = a.r^{5 – 1}
∴ 243 = a.r⁴……………. (ii)
परिणाम (i) का मान परिणाम (ii) में रखने पर

∴ 243 = ar.r³
∴ 243 = 9.r³
∴ r³ = \(\frac{243}{9}\)
∴ r³ = 27
∴ r³ = (3)³
∴ r = 3

परिणाम (i) में r = 3 रखने पर
ar = 9
∴ a × 3 = 9
∴ a = \(\frac {9}{3}\)
∴ a = 3
अब S₄ ज्ञात करना है इसलिए a = 3, r = 3 और n = 4 S_n के सूत्र में रखने पर यहाँ |r| > 1 है ।
∴ S_n = \(\frac{a\left(r^n-1\right)}{r-1}\)
S₄ = \(\frac{3\left(3^4-1\right)}{3-1}\)
= \(\frac{3(81-1)}{2}\)
= \(\frac{3 \times 80}{2}\)
∴ S₄ = 120
इसलिए S₄ = 120 होगा ।

प्रश्न 5.
गुणोत्तर-श्रेणी में प्रथमपद 10 है और T₄ = 0.08 हो, तो प्रथम तीन पदों का योग ज्ञात करो ।
उत्तर :
यहाँ प्रथमपद a = 10 और T₄ = ar³ = 0.08 दिया है ।
T_n = ar^{n – 1} में a = 10, T_n = 0.08, n = 4 रखने पर
0.08 = 10 × r^{4 – 1}
\(\frac{0.08}{10}\) = r³
0.008 = r³
(0.2)³ = r³ दोनों ओर घात की तुलना करने पर
∴ r = 0.2
अब प्रथम तीन पदों का योग करना है इसलिए
S_n = \(\frac{a\left(1-r^n\right)}{1-r}\) में a = 10, r = 0.2, n = 3 रखने पर
S₃ = \(\frac{10\left(1-(0.2)^3\right)}{1-0.2}=\frac{10(1-0.008)}{0.8}\) = \(\frac{10(0.992)}{0.8}=\frac{9.92}{0.8}\)
S₃ = 12.4
इसलिए प्रथम तीन पदों का योग = 12.4 होगा।

प्रश्न 6.
गुणोत्तर-श्रेणी के लिए T₁² = T₂ और T₃ = 64 हो, तो गुणोत्तर-श्रेणी लिखो ।
उत्तर :
T₁ = a और T₂ = ar, T₃ = ar² है
T₁² = T₂
∴ a² = ar
∴ \(\frac{\mathrm{a}^2}{\mathrm{a}}\) = r
∴ r = a
∴ T₃ = ar² = 64 a = r रखने पर
∴ r × r² = 64
∴ r³ = 64
∴ r³ = (4)³ दोनों ओर घात की तुलना करने पर
∴ r = 4

ar² = 64 में r = 4 रखने पर a × 4² = 64
∴ a × 16 = 64
∴ a = \(\frac{64}{16}\)
∴ a = 4

गुणोत्तर-श्रेणी T₁, T₂, T₃…….. के लिए श्रृंखला a, ar, ar² ….. बनेगी । a = 4 और r = 4 रखने पर श्रृंखला प्राप्त होगी ।
∴ 4, 4 × 4, 4 × (4)² …..
∴ 4, 16, 64 ….. श्रृंखला प्राप्त होगी ।

प्रश्न 7.
यदि 5, M, 20, t गुणोत्तर-श्रेणी में हो, तो m और t ज्ञात करो ।
उत्तर :
यहाँ 5, M, 20, t गुणोत्तर-श्रेणी में है ।
इसलिए \(\frac{T_2}{T_1}=\frac{T_3}{T_2}=\frac{T_4}{T_3}\) सामान्य अनुपात r होगा ।
\(\frac{T_2}{T_1}=\frac{T_3}{T_2}\)
∴ \(\frac{M}{5}=\frac{20}{M}\)
∴ m² = 100
∴ m = ± 10
∴ m = – 10 अथवा + 10
अब \(\frac{T_3}{T_2}=\frac{T_4}{T_3}\)
∴ \(\frac{20}{\mathrm{~m}}=\frac{\mathrm{t}}{20}\)
∴ mt = 20 × 20
∴ mt = 400
अब m = 10 रखने पर अथवा m = – 10 रखने पर
∴ 10 × t = + 400
∴ t = \(\frac{400}{10}\)
∴ t = 40

∴ -10 × t = 400
∴ t = \(\frac{400}{-10}\)
∴ t = -40
इस तरह m = 10 और t = 40 अथवा m = – 10 और t = – 40

प्रश्न 8.
दी गई गुणोत्तर-श्रेणी में a = 10, r = 0.1 और Tn = 0.01 हो, तो n ज्ञात करो।
उत्तर :
यहाँ a = 10, r = 0.1, T_n = 0.01 दिया है ।
T_n = ar^{n – 1} में a = 10, r = 0.1, T_n = 0.01 रखने पर
0.01 = 10 x (0.1)^{n – 1}
\(\frac{0.01}{10}\) = (0.1)^{n – 1}
0.001 = (0.1)^{n – 1}
= (0.1)³ = (0.1)^{n – 1} दोनों ओर घात की तुलना करने पर
n – 1 = 3
∴ n = 3 + 1 ∴ n = 4

प्रश्न 9.
दी गई गुणोत्तर-श्रेणी में a = 1, r = 3 और S_n = 121 हो, तो n ज्ञात करो ।
उत्तर :
यहाँ a = 1, r = 3, S_n = 121 दिया है ।
S_n = \(\frac{a\left(r^n-1\right)}{r-1}\) में a = 1, r = 3, S_n = 121 रखने पर
∴ 121 = \(\frac{1\left(3^n-1\right)}{3-1}\)
∴ 121 = \(\frac{1\left(3^n-1\right)}{2}\)
∴ 121 × 2 = 3^{n – 1}
∴ 242 + 1 = 3ⁿ
∴ 243 = 3ⁿ
∴ 3⁵ = 3ⁿ दोनों ओर घात की तुलना करने पर
n = 5
प्रथम चार पदों का योग 121 होगा अर्थात् S₅ = 121

प्रश्न 10.
यदि S_n = \(\frac{2}{3}\) (2ⁿ – 1) हो, तो T₄ ज्ञात करो ।
उत्तर :
हम जानते है कि T_{n + 1} = S_{n + 1} – S_n
∴ T₄ = S_{3 + 1} – S₃

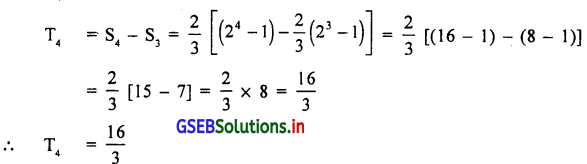
प्रश्न 11.
यदि S_n = 4 (3ⁿ – 1) हो, तो T_{n + 1} ज्ञात करो ।
उत्तर :
हम जानते है कि T_{n + 1} = S_{n + 1} – S_n
T_{n + 1} = 4 (3^{n + 1} – 1) – 4 (3ⁿ – 1)
= 4 (3^{n + 1} – 1 – 3ⁿ + 1) = 4 (3^{n + 1} – 3ⁿ)
= 4 (3ⁿ) (3 – 1) = 4 (3ⁿ) (2)
∴ T_{n + 1} = 8 (3ⁿ)

प्रश्न 12.
यदि गुणोत्तर-श्रेणी का दूसरा पद 5 हो, तो प्रथम तीन पदों का गुणनफल ज्ञात करो ।
उत्तर :
मानाकि प्रथमपद = a और सामान्य अनुपात = r है ।
दूसरा पद 5 है अर्थात् T₂ = 5
n = 1, n = 2, n = 3 को T_n = ar^{n – 1} में रखने पर T₁ = a, T₂ = ar, T₃ = ar² प्राप्त होगा ।
T₁ × T₂ × T₃ = a × ar × ar² T₂ = 5
= a³ × r³ ∴ ar = 5 रखने पर
= (ar)³ = (5)³ = 125
प्रथम तीन पदों का गुणनफल 125 है ।

प्रश्न 13.
गुणोत्तर-श्रेणी 2, 4, 8, 16 …. के कितने पदों का योग 126 होगा ?
उत्तर :
यहाँ a = 2 और सामान्य अनुपात r = \(\frac{\mathrm{T}_2}{\mathrm{~T}_1}=\frac{4}{2}\) = 2
प्रथम n पदों का योग 126 है ।
∴ S_n = \(\frac{a\left(r^n-1\right)}{r-1}\) में a = 2, r = 2, S_n = 126 रखने पर
∴ 126 = \(\frac{2\left(2^n-1\right)}{2-1}\)
∴ \(\frac{126}{2}\) = 2ⁿ – 1
∴ 63 + 1 = 2ⁿ
∴ 2ⁿ = 64
∴ 2ⁿ = 2⁶ दोनों ओर घात की तुलना करने पर
n = 6
प्रथम 6 पदों का योग 126 होगा ।

प्रश्न 14.
एक गुणोत्तर-प्रेणी में T_n – 324, S_n – 484 और r = 3 हो, तो a और n ज्ञात करो ।
उत्तर :
यहां T_n = 324, S_n = 484 और = 3 दिया है ।
इसलिए S_n = \(\frac{r_0 T_n-a}{r-1}\) यहाँ ।r। > 3 है ।
∴ 484 = \(\frac{3 \times 324-\mathrm{a}}{3-1}\)
∴ 484 × 2 = 972 – a
∴ 968 = 972 – a
∴ a = 972 – 968
∴ a = 4

अब T_n = ar^{n – 1} – 1 में a = 4, r = 3, T_n = 324 रखने पर
324 = 4 × 3^{n – 1}
∴ \(\frac{324}{4}\) = 3^{n – 1}
∴ 81 = 3^{n – 1}
∴ 3⁴ = 3^{n – 1}
4 = n – 1
∴ n – 1 = 4
∴ n = 4 + 1
∴ n = 5
दोनों ओर घात की तुलना करने पर
a = 4 और n = 5 प्राप्त होगा ।

प्रश्न 15.
निम्न दी गई गुणोत्तर-श्रेणी का मान श्रेढीसूत्र से ज्ञात करो ।
उत्तर :
(1) 4, 16, 64… (4 पदों का योग)

(2) 2, 3, \(\frac {9}{2}\)… (5 पदों का योग)
यहाँ a = 2 सामान्य गुणोत्तर r = \(\frac{T_2}{T_1}=\frac{3}{2}\), n = 5
S_n = \(\frac{a\left(r^n-1\right)}{r-1}\) यहाँ |r| > 1 है ।

(3) 100, 20, 4… (5 पदों का योग) ।
यहाँ a = 100, सामान्य गुणो ‘ सामान्य गुणोत्तर r = \(\frac{\mathrm{T}_2}{\mathrm{~T}_1}=\frac{20}{100}\) = 0.2 n = 5
यहाँ |r| < 1 है ।

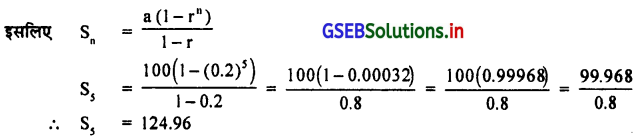
(4) \(\frac {1}{2}\), \(\frac {1}{4}\), \(\frac {1}{8}\) … (10 पदों का योग)

विभाग – E

निम्न के हल प्राप्त करो ।

प्रश्न 1.
तीन पन संख्याएँ K + 4, 4K – 2 और 7K + 1 गुणोत्तर-श्रेणी में है तो K ज्ञात करो ।
उत्तर :
यहाँ K + 4, 4K – 2, 7K + 1 गुणोत्तर-श्रेणी में है । इसलिए \(\frac{\mathrm{T}_2}{\mathrm{~T}_1}=\frac{\mathrm{T}_3}{\mathrm{~T}_2}\) = सामान्य गुणोत्तर r होगा ।
∴ \(\frac{4 K-2}{K+4}=\frac{7 K+1}{4 K-2}\)
∴ (4K – 2)² = (7K + 1) (K + 4)
∴ 16K² – 16K + 4 = 7K² + 29K + 4
∴ 16K² – 16K + 4 – 7K² – 29K – 4 = 0
∴ 9K² – 45K = 0
∴ 9K (K – 5) = 0
∴ 9K = 0 अथवा K – 5 = 0
∴ K = 0 अथवा K = 5

K = 0 के लिए 4K – 2 का मूल्य -2 प्राप्त होता है जो ऋण है इसलिए K = 0 स्वीकार्य मान नहि है । इसलिए K = 5 होगा ।

प्रश्न 2.
गुणोत्तर-श्रेणी 1, 3, 3², 3³ के प्रथम n पदों का योग 365 से बढ़े नहि ऐसा n का महत्तम मूल्य ज्ञात करो ।
उत्तर :

यहाँ प्रथमपद a = 1, सामान्य अनुपा r = \(\frac{T_2}{T_1}=\frac{3}{1}\) = 3 n पदों का योग 365 से बढ़े नहि अर्थात् S_n ≤ 365
S_n = \(\frac{\mathrm{a}\left(\mathrm{r}^{\mathrm{n}}-1\right)}{\mathrm{r}-1}\) में a, r, S_n रखने पर
S_n = \(\frac{1\left(3^n-1\right)}{3-1}=\frac{3^n-1}{2}\)
S_n ≤ 365 होने से
∴ \(\frac{3^n-1}{2}\) ≤ 365
∴ 3ⁿ ≤ 365 × 2 + 1
∴ 3ⁿ ≤ 731

n के विविध धन पूर्णांक मूल्यों के लिए 3″ का मूल्य की सारणी प्राप्त करेंगे और n की जिस मूल्य के लिए 3ⁿ ≤ 731 हो ऐसी n की महत्तम मूल्य लेंगे ।

सारणी पर से n = 5 के लिए 3ⁿ = 243, n = 6 के लिए 3ⁿ = 729 और n = 7 के लिए 2187 है जो 731 से अधिक है ।
n = 6 के लिए n की महत्तम किंमत है जिससे 3ⁿ ≤ 731 है ।
∴ n = 6

प्रश्न 3.
गुणोत्तर-श्रेणी 1, 2, 2², 2³…. के प्रथम n पदों का योग 2000 या उससे अधिक हो ऐसी n की लघुत्तम मूल्य ज्ञात करो ।
उत्तर :
यहाँ प्रथमपद a = 1 सामान्य अनुपात r = \(\frac{2}{1}\) = 2 n पदों का योग 2000 या उससे अधिक हो अर्थात् S_n ≥ 2000
a और r को S_n = \(\frac{a\left(r^n-1\right)}{r-1}\) में रखने पर
S_n = \(\frac{1\left(2^n-1\right)}{2-1}\) = 2ⁿ – 1
अब S_n ≥ 2000 है ।
∴ 2ⁿ – 1 ≥ 2000
∴ 2ⁿ ≥ 20001
अब n के विविध मूल्यों के लिए 2″ के मूल्यों की सारणी निम्नानुसार बनेगी और n की जो धन पूर्णांक मूल्य के लिए 2ⁿ ≥ 20001 हो ऐसी लघुतम किंमत प्राप्त करेंगे ।

कोष्टक पर से देखा जाता है कि n = 11, 12… के लिए 2ⁿ ≥ 20001 है ।
∴ n की लघुतम किंमत 11 है ।
∴ n = 11

प्रश्न 4.
गुणोत्तर-श्रेणी x, \(\frac{x}{3}, \frac{x}{9}\)……. (जहाँ x > 0) के प्रथम 5 पदों का योग 121 हो, तो x ज्ञात करो ।
उत्तर :

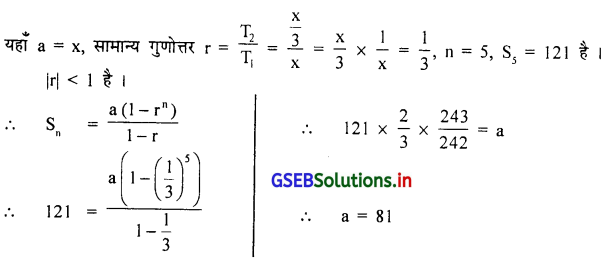
प्रश्न 5.
गुणोत्तर-श्रेणी में S₄ = 1052 हो, तो सामान्य गुणोत्तर ज्ञात करो ।
उत्तर :
यहाँ S₄ = 1052 दिया है ।

प्रश्न 6.
गुणोत्तर-श्रेणी में पाँचवा और तीसरा पदों का योग और अंतर 5 : 3 के अनुपात में है, तो सामान्य गुणोत्तर ज्ञात करो ।
उत्तर :
पाँचवा और तीसरा पदों का योग T₅ + T₃ होगा ।
पाँचवा और तीसरा पदों का अंतर T₅ – T₃ होगा ।
अब T₅ + T₃ : T₅ – T₃ = 5 : 3

प्रश्न 7.
एक गुणोत्तर-श्रेणी में तीन क्रमिक पदों का योग 31 तथा गुणाकार 125 है, तो उस श्रेणी के तीन पदों को ज्ञात करो ।
उत्तर :
मानाकि वे संख्याएँ =, \(\frac{a}{r}\), a, ar है ।
उनका गुणनफल = \(\frac{a}{r}\) × a × ar = 125
∴ a³ = 125
∴ a³ = 5³
∴ a = 5
उनका योगफल \(\frac{a}{r}\) + a + ar = 31
∴ \(\frac{5}{r}\) + 5 + 5r = 31
∴ \(\frac{5}{r}\) + 5r = 31 – 5
∴ \(\frac{5}{r}\) + 5r = 26
∴ 5 + 5r² – 26r = 0
5r² – 26r + 5 = 0
5r² – 25r – r + 5 = 0
5r (r – 5) – 1 (r – 5) = 0
5r – 1 = 0 अथवा r – 5 = 0
∴\(\frac{1}{5}\) अथवा r = 5
\(\frac{a}{r}\) a, a, ar में r = 5 और a = 5 रखने पर
\(\frac{5}{5}\), 5, 5 × 5
1, 5, 25
a = 5 r = \(\frac{1}{5}\) लेने पर
25, 5, 1 मिलेगी ।

प्रश्न 8.
एक गुणोत्तर-श्रेणी में तीन क्रमिक पदों का योग 6 और गुणनफल -64 है, तो श्रृंखला के तीनों पद ज्ञात करो ।
उत्तर :
माना कि श्रृंखला के पद \(\frac{a}{r}\), a, ar है ।
इन पदों का गुणनफल = \(\frac{a}{r}\) × a × ar = – 64
∴ a³ = – 64 घनमूल लेने पर
a = – 4
पदों का योगफल = \(\frac{a}{r}\) + a + ar = 6 a = – 4 लेने से
\(\frac{-4}{r}\) + (-4) + (-4r) = 6
∴ \(\frac{-4}{r}\) – 4r = 6 + 4
∴ \(\frac{-4}{r}\) – 4r = 10 r से गुणा करने पर
∴ – 4 – 4r² = 10r
∴ – 4r² – 10r – 4 = 0 चिह्न बदलने पर
4r² + 10r + 4 = 0 2 से भाग देने पर
2r² + 5r + 2 = 0
∴ 2r² + 4r + r + 2 = 0
2r (r + 2) + 1 (r + 2) = 0
2r + 1 = 0 अथवा r + 2 = 0
∴ r = \(\frac{-1}{2}\) अथवा r = – 2

अंब \(\frac{\mathbf{a}}{r}\), a, ar में a = – 4 और r = – 2 रखने पर
\(\frac{-4}{-2}\), -4, -4 × -2
2, -4, 8 होंगे ।
a = – 4 और r = –\(\frac{1}{2}\) बने पर गुणोत्तर-श्रेणी के पद 8, -4, 2 होंगे ।

प्रश्न 9.
एक भवन-निर्माण व्यवसाय में कार्यरत कंपनी ग्राहकों को आकर्षित करने हेतु फ्लैट्स की एक योजना प्रस्तुत करती है । इस योजना में ग्राहक को प्रथम किश्त में 10,000 रुपिया एवं तत्पश्चात् प्रत्येक वार्षिक किश्त उससे पहले चुकाए गए किश्त से दुगनी राशि चुकाना है । 10 किश्तों के अंत में उस ग्राहक ने कुल कितनी राशि चुकाई होगी ?
उत्तर :
प्रथम किश्त 10,000 रु. है ∴ a = 10,000
प्रत्येक किश्त की राशि उससे पहले चुकाए गए किश्त की राशि से दुगुनी है । ∴ r = 2
10 किश्तों के अंत में चुकाई कुल रकम
S_n = \(\frac{\mathrm{a}\left(\mathrm{r}^{\mathrm{n}}-1\right)}{\mathrm{r}-1}\)
∴ S₁₀ = \(\frac{10000\left(2^{10}-1\right)}{2-1}\)
S₁₀ = 10000 (1024 – 1)
= 10000 (1023)
= 10230000
इस प्रकार ग्राहक द्वारा चुकाई गई दस हप्तों की कुल रकम 10230000 रु. होगी ।

प्रश्न 10.
एक बेंकर प्रथम मिनिट में 128 नोट की गिनती करता है । और उसके बाद वह प्रत्येक मिनिट उससे पहले की अपेक्षा आधी नोटों की गिनती करता है । तो वह 5 मिनिट में कितनी नोट की गिनती करेगा ?
उत्तर :
प्रथम मिनिट में 128 नोटो की गिनती करता है । ∴ a = 128
उसके बाद उससे पहले की मिनिट से आधि गिनती करता है ।
∴ r = \(\frac{064}{128}\) = 0.5 प्रथम 5 मिनिट का योग ज्ञात करना है । ∴ n = 5
128 यहाँ |r| < 1 है ।

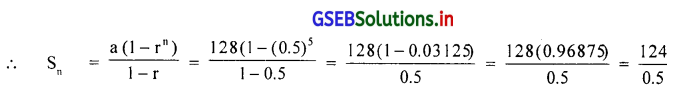
∴ S₅ = 248 नोटो
प्रथम 5 मिनिट में 248 नोटो की गिनती करेगा ।

प्रश्न 11.
एक गाँव की जनसंख्या 5000 है । यदि जनसंख्या में प्रति वर्ष 2 प्रतिशत की वृद्धि हो, तो दस साल के बाद उस गाँव की जनसंख्या कितनी होगी ?
उत्तर :
गाव की जनसंख्या 5000 है । ∴ a = 5000
2 प्रतिशत की वृद्धि होती है । T₂ = 5000 × 1.02
∴ r = \(\frac{100+2}{100}\) = 1.02 T₂ = 5100
10 वर्ष के बाद की जनसंख्या ज्ञात करना है n = 11
a, r, n का मूल्य T₁₁ = ar^{n – 1} में रखने पर
T₁₁ = 5000 × (1.02)^{11 – 1}
= 5000 × (1.02)¹⁰
= 5000 × 1.218994
T₁₁ = 6095
दस साल के बाद उस गाँव की जनसंख्या 6095 होगी ।

प्रश्न 12.
एक कार के मूल्य में प्रतिवर्ष 10% घिसाई होती है। यदि कार की क्रयमूल्य 5,00,000 रुपिया हो, तो 6 वर्ष के बाद कार का मूल्य कितना होगा ?
उत्तर :
कार का क्रयमूल्य 5,00,000 रुपिया है । ∴ a = 5,00,000
घिसाई प्रति वर्ष 10% है । ∴ r = \(\frac{100-10}{100}=\frac{90}{100}\) = 0.9
6 वर्ष के बाद कार का मूल्य ज्ञात करना है अर्थात् n = 7
a, r, n का मूल्य T_n = ar^{n – 1} में रखने पर
T₇ = 500000 (0.90)^{7 – 1}
= 500000 (0.90)⁶
= 500000 × 0.531441
= 265720.5 6 वर्ष के बाद कार का मूल्य 2,65,720.50 रुपिया होगा ।