Gujarat Board Statistics Class 12 GSEB Solutions Part 1 Chapter 3 रैखिक नियत-सम्बन्ध Ex 3.2 Textbook Exercise Questions and Answers.
Gujarat Board Textbook Solutions Class 12 Statistics Part 1 Chapter 3 रैखिक नियत-सम्बन्ध Ex 3.2
प्रश्न 1.
कपास की फसल पर खाद का उपयोग का प्रभाव जानने हेतु एक अभ्यास में से निम्नानुसार सूचना प्राप्त हुई है ।

उपयु क्त सूचना से y की x पर की नियत सम्बन्ध रेखा प्राप्त कीजिए और खाद का उपयोग 300 किग्रा हुआ हो, तो प्रति हेक्टर कपास की फसल का अनुमान कीजिए ।
उत्तर :
यहाँ n = 7, \(\bar{x}=\frac{\sum x}{n}=\frac{177}{7}\) = 25.29, \(\overline{\mathrm{y}}=\frac{\sum \mathrm{y}}{\mathrm{n}}=\frac{830}{7}\) = 118.57
हम A = 25, B = 118 लेकर u और v निम्नानुसार पारिभाषित करेंगे । u = x – A = x – 25, v = y – B = y – 118
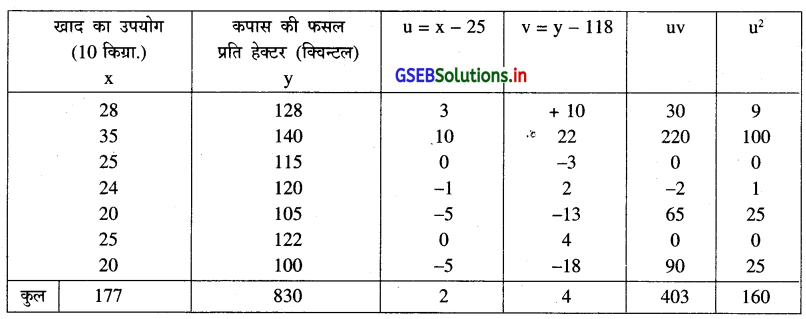
संक्षिप्त विधि से b का मूल्य निम्नानुसार ज्ञात करेंगे ।
b = byx = bvu = \(\frac{\mathrm{n} \sum u \mathrm{u}-\left(\sum \mathrm{u}\right)\left(\sum \mathrm{v}\right)}{\mathrm{n} \sum \mathrm{u}^2-\left(\sum \mathrm{u}\right)^2}\)
= \(\frac{7 \times 403-(2)(4)}{7 \times 160-(2)^2}\)
= \(\frac{2821-8}{1120-4}\)
= \(\frac{2813}{1116}\)
∴ b = 2.52
अब a = \(\overline{\mathrm{y}}\) – b\(\overline{\mathrm{x}}\)
= 118.57 – 2.52 (25.29)
= 118.57 – 63.73
= 54.84
∴ a = 54.84
अत: y की x पर की नियत संबंध रेखा
ŷ = a + bx
= 54.84 + 2.52x
∴ ŷ = 54.84 + 2.52x
x = \(\frac{300}{10}\) = 30 रखने पर (खाद का उपयोग 10 किग्रा में है ।)
ŷ = 54.84 + 2.52 (30)
= 54.84 + 75.6
= 130.44 (क्विन्टल)
यदि खाद का उपयोग 300 किग्रा किया जाय तो कपास की फसल प्रतिहेक्टर 130.44 (क्विन्टल) होने का अनुमान है ।
![]()
प्रश्न 2.
पिता और पुत्र की ऊँचाई के बीच का सम्बन्ध की जाँच के लिए पिता और उसके वयस्क पुत्र की आठ युग्मों की निम्न सूचना पर से पुत्र की ऊँचाई की पिता की ऊँचाई पर से नियत संबंध रेखा प्राप्त कीजिए । जब किसी पिता की ऊँचाई 170 सेमी हो तब उसके पुत्र की ऊँचाई का अनुमान क्या ?

उत्तर :
यहाँ n = 8, \(\bar{x}=\frac{\sum x}{n}=\frac{1346}{8}\) = 168.25, \(\bar{y}=\frac{\sum y}{n}=\frac{1338}{8}\) = 167.25 । हम A = 168 और B = 167 लेकर u और v को निम्नानुसार पारिभाषित करेंगे । u = x – A = x – 168, v = y – B = y – 167
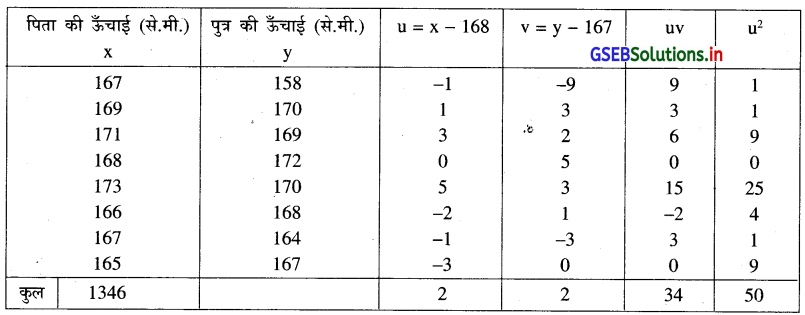
संक्षिप्त विधि से b का मूल्य निम्नानुसार ज्ञात करेंगे ।
b = byx = bvu = \(\frac{\mathrm{n} \sum u v-\left(\sum u\right)\left(\sum v\right)}{n \sum u^2-\left(\sum u\right)^2}\)
= \(\frac{8 \times 34-(2)(2)}{8 \times 50-(2)^2}\)
= \(\frac{272-4}{400-4}\)
= \(\frac{268}{396}\)
= 0.677
∴ b = 0.68
\(\overline{\mathrm{x}}\), \(\overline{\mathrm{y}}\) और b के मान a के सूत्र में रखने पर a = \(\overline{\mathrm{y}}\) – b\(\overline{\mathrm{x}}\)
= 167.25 – 0.68 (168.25)
= 167.25 – 114.41
= 52.84
∴ a = 52.84
अतः y की x पर की नियत सम्बन्ध रेखा
ŷ = a + bx
ŷ = 52.84 + 0.68x
∴ ŷ = 52.84 + 0.68x
x = 170 रखने पर
ŷ = 52.84 + 0.68 (170)
= 52.84 + 115.6
= 168.44 सेमी
पिता की ऊँचाई 170 सेमी हो तब पुत्र की ऊँचाई 168.44 सेमी होने का अनुमान है ।
प्रश्न 3.
समुद्री स्तर से स्थान की ऊँचाई (attitude) और उस स्थान पर हवा में असरकारक ओक्सिजन का प्रमाण की निम्न सूचना पर से प्रभावक ऑक्सिजन का प्रमाण y की समुद्री स्तर से ऊँचाई (x) पर की नियतसंबंध रेखा प्राप्त कीजिए । (305 मीटर = 1000 फिट) स्थान की ऊँचाई (305 मीटर)

जब किसी स्थान की समुद्री सतह से ऊँचाई 7 इकाई (1 इकाई = 305 मीटर) हो, तो हवा में ऑक्सिजन के प्रतिशत अनुमान प्राप्त कीजिए।
उत्तर :
यहाँ n = \(\bar{x}=\frac{\sum x}{n}=\frac{21}{7}\) = 3, \(\overline{\mathrm{y}}=\frac{\Sigma \mathrm{y}}{\mathrm{n}}=\frac{130.1}{7}\) = 18.59 । \(\overline{\mathrm{x}}\) और \(\overline{\mathrm{y}}\) अपूर्णांक में प्राप्त होता है y के मूल्य में दशांश के बाद एक अंक है । A = 3 और B = 18.6, Cx = 1 और Cy = \(\frac{1}{0.1}\) लेकर सारणी बनायेंगे ।
u = \(\frac{\mathrm{x}-\mathrm{A}}{\mathrm{Cx}}=\frac{\mathrm{x}-3}{1}\), v = \(\frac{\mathrm{y}-\mathrm{B}}{\mathrm{Cy}}\) = v = \(\frac{y-18.6}{0.1}\)
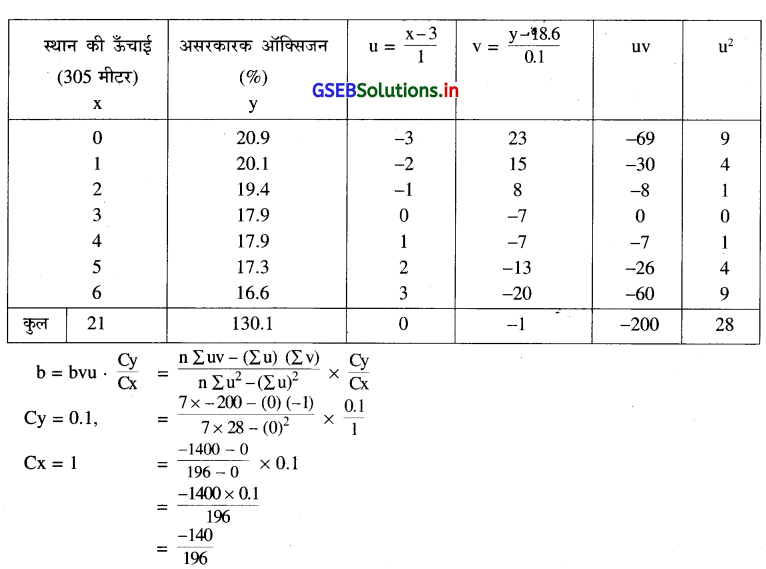
= -0.71
∴ b = -0.71
\(\overline{\mathrm{x}}\), \(\overline{\mathrm{y}}\) और b का मान a के सूत्र में रखने पर a = \(\overline{\mathrm{y}}\) – b\(\overline{\mathrm{x}}\)
= 18.59 – (-0.71)(3)
= 18.59 + 2.13
∴ a = 20.72
अत: y की x पर की नियत सम्बन्ध रेखा
ŷ = a + bx
= 20.72 – 0.71x
∴ ŷ = 20.72 – 0.71x
x = 7 रखने पर
ŷ = 20.72 – 0.71(7)
= 20.72 – 4.97
= 15.75
∴ ŷ = 15.75%
जब किसी स्थान समुद्री स्तर से 7 फूट ऊँचाई पर हो तब उस स्थान पर ऑक्सिजन का प्रतिशत 15.75% होने का अनुमान है ।
![]()
प्रश्न 4.
एक बड़े शहर में मकान में उपयोग का स्थान और मासिक किराया के बीच संबंध जानने के लिए निम्नानुसार सूचना एकत्रित की गई।

उस सूचना पर से y की x पर का नियतसंबंध रेखा ज्ञात कीजिए । यदि किसी मकान का उपयोग 110 वर्ग मीटर हो, तो उसका मासिक किराया कितना होगा, उसका अनुमान करो ।
उत्तर :
यहाँ n = 7, \(\bar{x}=\frac{\sum x}{n}=\frac{630}{7}\) = 90, \(\bar{y}=\frac{\sum y}{n}=\frac{182000}{7}\) = 26000 है । इसलिए संक्षिप्त विधि से b की गणना करेंगे ।
A = 90 और B = 26000 लेंगे । Cx = 5 और Cy = 1000
अब u = \(\frac{\mathrm{x}-\mathrm{A}}{\mathrm{Cx}}=\frac{\mathrm{x}-90}{5}\) और v = \(\frac{y-B}{C y}=\frac{y-26000}{1000}\) लेकर सारणी निम्नानुसार तैयार करेंगे ।
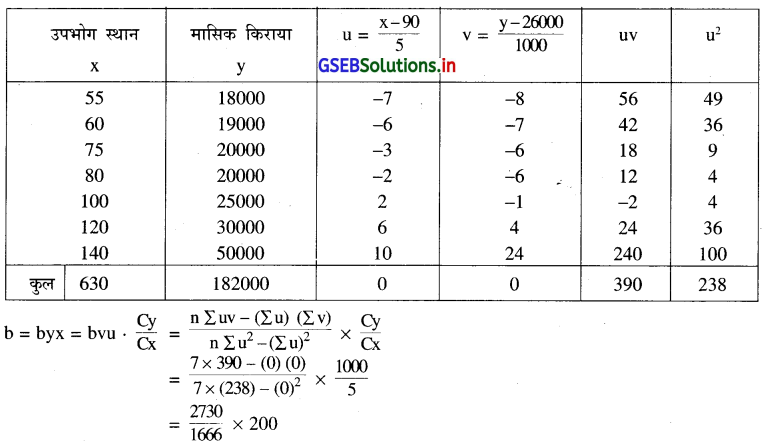
= 327.73
∴ b = 327.73
\(\overline{\mathrm{x}}\), \(\overline{\mathrm{y}}\) और b के मान a के सूत्र में रखने पर a = \(\overline{\mathrm{y}}\) – b\(\overline{\mathrm{x}}\)
= 26000 – 327.73 (90)
= 26000 – 29495.7
= 3495.7
a = -3495.7
अत: y की x पर की नियतसंबंध रेखा
ŷ = a + bx
ŷ = -3495.7 + 327.73 x
∴ ŷ = -3495.7 + 327.73x
x = 110 रखने पर
ŷ = -3495.7 + 327.73 (110)
= -3495.7 + 36050.3
ŷ = 32554.6 (रु.)
जब मकान का उपभोग 110 वर्ग मीटर होगा तब मकान का आकलित मासिक किराया 32554.6 रु. होगा ।
प्रश्न 5.
एक मोल में प्रतिदिन आनेवाले ग्राहकों की संख्या और बिक्री (दस हजार रु.) के बीच का संबंध जानने हेतु निम्नानुसार न्यादर्श जानकारी प्राप्त हुई है ।

इस जानकारी से y की x पर की नियतसम्बन्ध रेखा प्राप्त कीजिए । यदि किसी एक दिन 80 ग्राहक मोल की मुलाकात ले तो मोल में कितनी बिक्री हुई होगी ? उसका अनुमान कीजिए ।
उत्तर :
n = 6, \(\bar{x}=\frac{\sum x}{n}=\frac{560}{6}\) = 93.33, \(\overline{\mathrm{y}}=\frac{\sum \mathrm{y}}{\mathrm{n}}, \overline{\mathrm{y}}=\frac{14.4}{6}\) = 2.4
\(\overline{\mathrm{x}}\) और \(\overline{\mathrm{y}}\) अपूर्णांक में है । इसलिए संक्षिप्त विधि से b की गणना करेंगे । A = 100 और B = 2.4, Cx = 10 और Cy = 0.1
लेकर नया चर u = \(\frac{\mathrm{x}-\mathrm{A}}{\mathrm{Cx}}\) और v = \(\frac{\mathrm{y}-\mathrm{B}}{\mathrm{Cy}}\), u = \(\frac{x-100}{10}\), v = \(\frac{y-2.4}{0.1}\) लेकर निम्नानुसार सारणी तैयार करेंगे ।
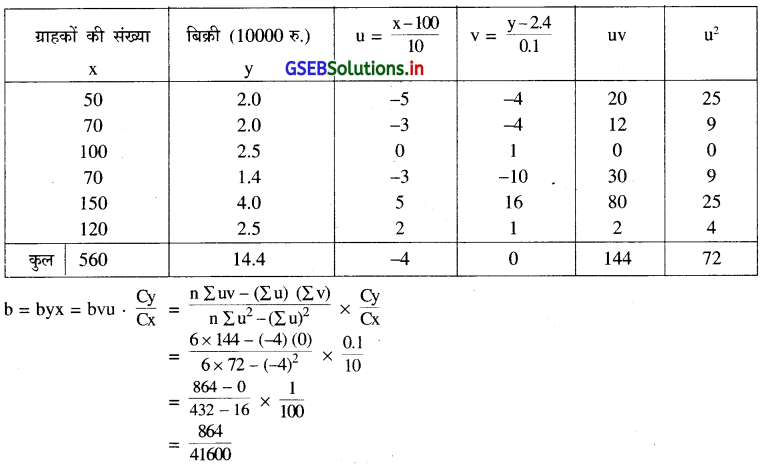
= 0.02
∴ b = 0.02
\(\overline{\mathrm{x}}\), \(\overline{\mathrm{y}}\) और b का मान a के सूत्र में रखने पर a = \(\overline{\mathrm{y}}\) – b\(\overline{\mathrm{x}}\)
= 2.4 – 0.02 (93.33)
= 2.4 – 1.87
= 0.53
∴ a = 0.53
अत: y की x पर की नियतसंबंध रेखा
ŷ = a + bx
ŷ = 0.53 + 0.02x
∴ ŷ = 0.53 + 0.02x
अब x = 80 रखने पर
ŷ = 0.53 + 0.02 (80)
= 0.53 + 1.6
= 2.13 (हजार रु.)
ŷ = 2.13 × 1000 = 2130 रु.
ग्राहकों की संख्या 80 हो तब ग्राहकों द्वारा की गई बिक्री
रु. 2130 होगा ।
![]()
प्रश्न 6.
एक शहर में कपड़े का व्यवसाय में कार्यरत दस पेढ़ीओं का औसत वार्षिक लाभ (लाख रु. में) और औसत वार्षिक प्रशासनिक खर्च (लाख्न रु. में) निम्नानुसार है ।
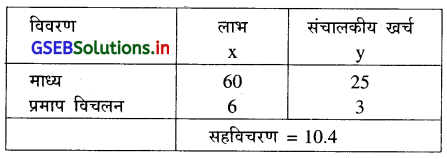
इस जानकारी से y का x पर का नियत संबंध रेखा ज्ञात कीजिए ।
उत्तर :
यहाँ \(\overline{\mathrm{x}}\) = 60, \(\overline{\mathrm{y}}\) = 25, Sx = 6, Sy = 3, Cov (x, y) = 10.4 दिया है ।
b = \(\frac{{Cov}(\mathrm{x}, \mathrm{y})}{\mathrm{Sx}^2}\)
= \(\frac{10.4}{(6)^2}\)
= \(\frac{10.4}{36}\)
= 0.289
∴ b = 0.29
और a = \(\overline{\mathrm{y}}\) – b\(\overline{\mathrm{x}}\)
= 25 – 0.29 (60)
= 25 – 17.4
= 7.6
∴ a = 7.6 अतः y की x पर की नियत संबंध रेखा
ŷ = a + bx
= 7.6 + 0.29x
∴ y = 7.6 + 0.29x
प्रश्न 7.
गुजरात के भिन्न भिन्न तहसील में गीरी वर्षा (सेमी में) और मक्के की फसल की उपज (क्विन्टल प्रति हेक्टर में) बीच संबंध जानने हेतु एकत्रित की गई सूचना पर से निम्न परिणाम प्राप्त हुए है ।
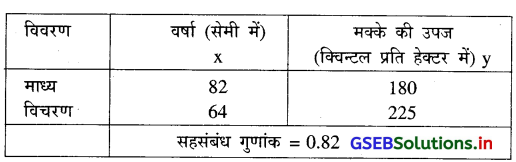
जब वर्षा 60 सेमी गीरे तब मक्के की उपज का अनुमान प्राप्त कीजिए ।
उत्तर :
यहाँ \(\overline{\mathrm{x}}\) = 82, \(\overline{\mathrm{y}}\) = 180, Sx2 = 64 .:. Sx = 8, Sy2 = 225 ∴ Sy = 15 और r = 0.82 दिया है ।
∴ b = r × \(\frac{\mathrm{Sy}}{\mathrm{Sx}}\)
= 0.82 × \(\frac{15}{8}\)
= 1.5375
∴ b = 1.54
और \(\overline{\mathrm{x}}\), \(\overline{\mathrm{y}}\) और b के मान a के सूत्र में रखने पर
a = \(\overline{\mathrm{y}}\) – b\(\overline{\mathrm{x}}\)
= 180 – 1.54 (82)
= 180 – 126.28
= 53.72
∴ a = 53.72
अत: y की x पर की नियतसंबंध रेखा
ŷ = a + bx
= 53.72 + 1.54x
∴ ŷ = 53.72 + 1.54x
अब x = 60 रखने पर
ŷ = 53.72 + 1.54 (60)
= 53.72 + 92.4
ŷ = 146.12 क्विन्टल
जब वार्षिक वर्षा 60 सेमी हो, तो होनेवाली आकलित उपज 146.12 क्विन्टल होगी ।
![]()
प्रश्न 8.
घडी की बेटरी (सेल) का मूल्य रु. में (x) और उसकी पूर्ति सो इकाई में (y) के बीच सम्बन्ध का अभ्यास करने के लिए एकत्रित की गई सूचना सार निम्नानुसार है ।
n = 10, Σx = 130, Σy = 220, Σx2 = 2288, Σxy = 3467
इस जानकारी से y का x के प्रति नियतसम्बन्ध रेखा ज्ञात कीजिए और मूल्य रु. 16 हो तब पूर्ति का अनुमान कीजिए ।
उत्तर :
यहाँ n = 10, \(\bar{x}=\frac{\sum x}{n}=\frac{130}{10}\) = 13, \(\overline{\mathrm{y}}=\frac{\Sigma \mathrm{y}}{\mathrm{n}}=\frac{220}{10}\) = 22, Σxy और Σx2 दिया है । इसलिए निम्नानुसार सूत्र का उपयोग करेंगे ।
b = \(\frac{n \Sigma x y-(\Sigma x)(\Sigma y)}{n \Sigma x^2-(\Sigma x)^2}\)
= \(\frac{10 \times 3467-(130)(220)}{10 \times 2288-(130)^2}\)
= \(\frac{34670-28600}{22880-16900}\)
= \(\frac{6070}{5980}\)
= 1.015
∴ b = 1.02
a = \(\overline{\mathrm{y}}\) – b\(\overline{\mathrm{x}}\)
= 22 – 1.02 (13)
= 22 – 13.26
= 8.74
∴ a = 8.74
अत: y की x पर की नियत सम्बन्ध रेखा
ŷ = a + bx
= 8.74 + 1.02x
∴ y = 8.74 + 1.02x
अब x = 16 रखने पर
ŷ = 8.74 + 1.02 (16)
= 8.74 + 16.32
∴ ŷ = 25.06 (सो इकाई) जब मूल्य 16 (रु.) हो तब पूर्ति 25.06 (सो इकाई) होने का अनुमान है ।
![]()
प्रश्न 9.
एक शहर में गर्मी में भिन्न-भिन्न छ दिनों दौरान महत्तम तापमान x और आईसक्रीम की बिक्री (y) की निम्न सूचना प्राप्त हुई है ।
महत्तम तापमान = x (सेल्सियस में)
आइस्क्रीम की बिक्री = y (लाख रु. में)
\(\overline{\mathrm{x}}\) = 40, \(\overline{\mathrm{y}}\) = 1.2, Σxy = 306, Sx2 = 20
इस जानकारी से आईसक्रीम की बिक्री का महत्तम तापमान प्रति नियतसम्बन्ध रेखा प्राप्त कीजिए । यदि किसी दिन महत्तम
तापमान 42 डिग्री सेल्सियस हो, तो उस दिन आईसक्रीम की बिक्री का आकलित मूल्य ज्ञात कीजिए ।
उत्तर :
यहाँ n = 6, \(\overline{\mathrm{x}}\) = 40, \(\overline{\mathrm{x}}\) = 1.2, Σxy = 306, Sx2 = 20 दिया है ।
अब b = \(\frac{{Cov}(\mathrm{x}, \mathrm{y})}{\mathrm{Sx}^2}\)
= \(\frac{\sum x y-n \bar{x} \bar{y}}{n \cdot S x^2}\)
= \(\frac{306-6 \times 40 \times 1.2}{6 \times 20}\)
= \(\frac{306-288}{120}\)
= \(\frac{18}{120}\)
= 0.15
∴ b = 0.15
a = \(\overline{\mathrm{y}}\) – b\(\overline{\mathrm{x}}\)
= 1.2 – 0.15 (40)
= 1.2 -6
= -4.8
∴ a = -4.8
अत: y की x पर की नियतसंबंध रेखा
ŷ = a + bx
= -4.8 + 0.15x
∴ ŷ = -4.8 + 0.15x
अब x = 42 रखने पर
ŷ = -4.8 + 0.15 (42)
= -4.8 + 6.3
ŷ = 1.5 (लाख रु.)
जब किसी दिन तापमान 42 डिग्री सेल्सीयस हो, तो उस दिन आईसक्रीम की बिक्री 1.5 (लाख रु.) होगी ।