GSEB Solutions Class 8 Maths Chapter 9 Algebraic Expressions and Identities InText Questions

/ By

Gujarat Board GSEB Textbook Solutions Class 8 Maths Chapter 9 Algebraic Expressions and Identities InText Questions and Answers.

Gujarat Board Textbook Solutions Class 8 Maths Chapter 9 Algebraic Expressions and Identities InText Questions

Try These (Page 138)

Question 1.
Give five examples of expressions containing one variable and five examples of expressions containing two variables?
Solution:
(a) Five examples containing one variable are:

  • x – 4
  • 5 – y
  • 2x + 5
  • 10x + 4
  • 11 – z

(b) Five examples containing two variables are:

  • 7x – 2y
  • 5x + 2y – 10
  • 6x + z – 2
  • 15y – z
  • 9x – 10z

GSEB Solutions Class 8 Maths Chapter 9 Algebraic Expressions and Identities InText Questions

Question 2.
Show on the number line x, x – 4, 2x + 1, 3x – 2.
Solution:
(i)
GSEB Solutions Class 8 Maths Chapter 9 Algebraic Expressions and Identities InText Questions img 1
The point X represent the variable ‘x’.

(ii)
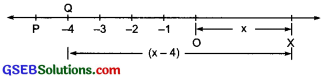
GSEB Solutions Class 8 Maths Chapter 9 Algebraic Expressions and Identities InText Questions img 2

(iii)
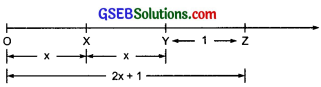
GSEB Solutions Class 8 Maths Chapter 9 Algebraic Expressions and Identities InText Questions img 3

(iv)
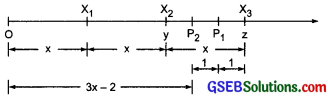
GSEB Solutions Class 8 Maths Chapter 9 Algebraic Expressions and Identities InText Questions img 4

Try These (Page 138)

Question 1.
Identify the coefficient of each term in the expression
x2y2 – 10x2y + 5xy2 – 20?
Solution:
Coefficient of x2y2 is 1.
Coefficient of x2y is -10.
Coefficient of xy2 is 5.

Try These (Page 138)

Question 1.
Classify the following polynomials as monomials, binomials, trinomials -z + 5, x + y + z, y + z + 100, ab – ac, 17
Solution:
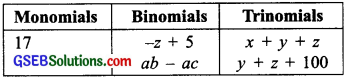
GSEB Solutions Class 8 Maths Chapter 9 Algebraic Expressions and Identities InText Questions img 5

GSEB Solutions Class 8 Maths Chapter 9 Algebraic Expressions and Identities InText Questions

Question 2.
Construct:
(a) 3 binomials with only x as a variable
(b) 3 binomials with x and y as variable
(c) 3 monomials with x and y as variables
(d) 2 polynomials with 4 or more terms
Solution:
(a)

  • 5x – 4
  • 3x + 2
  • 10 + 2x

(b)

  • 2x + 3y
  • 5x – y
  • x – 3y

(c)

  • 2xy
  • xy
  • -7xy

(d)

  • 2x3 – x2 + 6x – 8
  • 10 + 7x – 2x2 + 4x3

Try These (Page 139)

Question 1.
Write two terms which are like

  1. 7xy
  2. 4mn2
  3. 2l

Solution:

  1. Two terms like 7xy are: -3xy and 8xy.
  2. Two terms like 4mn2 are: 6mn2 and -2n2m.
  3. Two terms like 2l are: 5l and -7b.

Try These (Page 143)

Question 1.
Find 4x × 5y × 7z. First find 4x × 5y and multiply it by 7z; or fIrst find 5y × 7z and multiply it by 4x. Is the result the same? What do you observe? Does the order in which you carry out the multiplication marier?
Solution:
We have
4x × 5y × 7z = (4x × 5y) × 7z
= 20xy × 7z = 140 xyz
Also 4x × 5y × 7z = 4x × (5y × 7z)
= 4x × 35yz = 140 xyz
We observe that
(4x × 5y) × 7x = 4 × (5y × 7z)
∴ The product of monomials is associative, i.e. the order in which we multiply the monomials does not matter.

Try These (Page 144)

Question 1.
Find the product

  1. 2 x (3x + 5xy)
  2. a2 (2ab – 5c)

Solution:
1. 2x(3x + 5xy) = 2x × 3x + 2x × 5xy
= (2 × 3) × x × x + (2 × 5) × x × xy

2. a2(2ab – 5c) = a2 × 2ab + a2 × (-5c)
= (1 × 2) × a2 × ab + [1 × (-5)] × a2 × c
= 2 × a3b + (-5) × a2c = 2a3b – 5a2c

Try These (Page 145)

Question 1.
Find the product: (4p2 + 5p + 7) × 3p
Solution:
(4p2 + 5p + 7) × 3p
= (4p2 × 3p) + (5p × 3p) + (7 × 3p)
= [(4 × 3) × p2 × p] + [(5 × 3) × p × p] + (7 × 3) × p
= 12 × p3 + 15 × p2 + 21 × p
= 12p3 + 15p2 + 21p

GSEB Solutions Class 8 Maths Chapter 9 Algebraic Expressions and Identities InText Questions

Question 2.
Simplify: 2x(x – 1) + 5 and find its value at x = -1.
Solution:
2x(x – 1) + 5 = [2x × x] + [2x × (-1)] + 5
= [(2 × 1) × x × x] + [2 × (-1) × x] + 5
= [2 × x2] + [-2 × x] + 5
= 2x2 – 2x + 5
For x = -1, 2x2 – 2x + 5
= 2(-1)2 – 2(-1) + 5
= (2 × 1) – (-2) + 5
= 2 + 2 + 5 = 9

GSEB Solutions Class 8 Maths Chapter 9 Algebraic Expressions and Identities InText Questions

Question 3.
Carry out the multiplication of the expressions in each of the following pairs?

  1. 4p, q + r
  2. ab, a – b
  3. a + b, 7a2b2
  4. a2 – 9, 4a
  5. pq + qr + rp, 0

Solution:
1. 4p × (q + r) = (4p × q) + (4p × r)
= (4 × 1) × p × q + (4 × 1) × p × r
= 4 × pq + 4 × pr = 4pq + 4pr

2. ab × (a – b) = ab × a + ab × (-b)
= (1 × 1) × ab × a + [1 × (-1)] × ab × b
= 1 × a2 × b + (-1) × a × b2
= a2b – ab2

3. (a + b) × 7a2b2 = a × 7a2b2 + b + 7a2b2
= (1 × 7) × a × a2b2 + (1 × 7) × b × a2b2
= 7 × a3b2 + 7 × a2b3 = 7a3b2 + 7a2b3

4. (a2 – 9) × 4a = a2 × 4a + (-9) × 4a
= (1 × 4) × a2 × a + (-9 × 4) × a
= 4 × a3 + (-36) × a
= 4a3 – 36a

5. (pq + qr + rp) × 0
= pq × 0 + qr × 0 + rp × 0
= 0 + 0 + 0 = 0

Try These (Page 148)

Question 1.
Multiply the binomials.

  1. (2x + 5) and (4x – 3)
  2. (y – 8) and (3y – 4)
  3. (2.51 – 0.5m) and (2.51 + 0.5m)
  4. (a + 3b) and (x + 5)
  5. (2pq + 3q2) and (3pq – 2q2)
  6. (\(\frac{3}{4}\) a2 + 3b2) and 4 (a2 – \(\frac{2}{3}\)b2)

Solution:
1. (2x + 5) × (4x – 3)
= 2x(4x – 3) + 5(4x – 3)
= (2x × 4x) – (2x × 3) + (5 × 4x) – (5 × 3)
= (8x2) – 6x + 20x – 15
= 8x2 + (-6 + 20)x – 15
= 8x2 + 14x – 15

2. (y – 8) × (3y – 4) = y(3y – 4) – 8(3y – 4)
= (3y × y) – (4 × y) – 8 × 3y – 8 × (-4)
= 3y2 – 4y – 24y + 32
= 3y2 – 28y + 32

3. (2.5l – 0.5m) × (2.5l + 0.5m)
= 2.5l(2.5l + 0.5m) – 0.5m(2.5l + 0.5m)
= (2.5l × 2.5l) + (2.5l × 0.5m) – (2.5l × 0.5m) – (0.5m × 0.5m)
= 6.25l2 + 1.25lm – 1.25lm – 0.25m2
= 6.25l2 + (0)lm – 0.25m2 = 6.25l2 – 0.25m2

4. (a + 3b) × (x + 5)
= a × (x × 5) + 3b × (x + 5)
= (a × x) + (a × 5) + (3b × x) + (3b × 5)
= ax + 5a + 3bx + 15b

5. (2pq + 3q2) × (3pq – 2q2)
= 2pq(3pq – 2q2) + 3q2(3pq – 2q2)
= (2pq × 3pq) – (2pq × 2q2) + (3q2 × 3pq) – (3q2 × 3pq) – (3q2 × 2q2)
= 6p2q2 – 4pq3 + 9pq3 – 6q4
= 6p2q2 + (-4 + 9)pq3 – 6q4
= 6p2q2 + 5pq3 – 6q4

6. (\(\frac{3}{4}\)a2 + 3b2) × 4(a2 – \(\frac{2}{3}\)b2)
= \(\frac{3}{4}\)a2 × 4(a2 – \(\frac{2}{3}\)b2) + 3b2 × 4(a2 – \(\frac{2}{3}\)b2)
= (3a2 × a2) – (3a2 × \(\frac{2}{3}\)b2) + (12b2 × a2) – (12b2 × \(\frac{2}{3}\)b2)
= 3a4 – 2a2b2 + 12a2b2 – 8b4
= 3a4 + (-2 + 12)a2b2 – 8b4
= 3a4 + 10a2b2 – 8b4

GSEB Solutions Class 8 Maths Chapter 9 Algebraic Expressions and Identities InText Questions

Question 2.
Find the product:

  1. (5 – 2x)(3 + x)
  2. (x + 7y)(7x – y)
  3. (a2 + b)(a + b2)
  4. (p2 – q2) (2p + q)

Solution:
1. (5 – 2x) × (x + 3) = 5(x + 3) – 2x(x + 3)
= 5x + 15 – (2x × x) – (2x × 3)
= 5x + 15 – 2x2 – 6x
= -2x2 + (-6 + 5)x + 15
= -2x2 – x + 15 = 15 – x – 2x2

2. (x + 7y) × (7x – y) = x(7x – y) + 7y(7x – y)
= (x × 7x) – (x × y) + (7y × 7x) – (7y × y)
= 7x2 – xy + 49xy – 7y2
= 7x2 + 48xy – 7y2

3. (a2 + b) (a + b2) = a2(a + b2) + b(a + b2)
= (a2 × a) + (a2 × b2) + (b × a) + (b × b2)
= a3 + a2b2 + ab + b3

4. (p2 – q2) × (2p + q) = p2(2p + q) – q2(2p + q)
= (p2 × 2p) + (p2 × q) – (q2 × 2p) – (q2 × q)
= 2p3 + p2q – 2pq2 – q3

GSEB Solutions Class 8 Maths Chapter 9 Algebraic Expressions and Identities InText Questions

Question 3.
Simplify:

  1. (x2 – 5)(x + 5) + 25
  2. (a2 + 5) (b3 + 3) + 5
  3. (t + s2)(t2 – s)
  4. (a + b)(c – d) + (a – b)(c + d) + 2(ac + bd)
  5. (x + y) (2x + y) + (x + 2y) (x – y)
  6. (x + y)(x2 – xy + y2)
  7. (1.5x – 4y)(1.5x + 4y + 3) – 4.5x + 12y
  8. (a + b + c)(a + b – c)

Solution:
1. (x2 – 5)(x + 5) + 25
= x2(x + 5) -5(x + 5) + 25
= (x2 × x) + (x2 × 5) – (5 × x) – (5 × 5) + 25
= x3 + 5x2 – 5x – 25 + 25
= x3 + 5x2 – 5x

2. (a2 + 5)(b3 + 3) + 5 = a2(b3 + 3) + 5(b3 + 3) + 5
= (a2 × b3) + (a2 × 3) + (5 × b3) + (5 × 3) + 5
= a2b3 + 3a2 + 5b3 + 15 + 5
= a3b3 + 3a2 + 5b3 + 20

3. (t + s2) × (t2 – s) = t(t2 – s) + s2(t2 – s)
= (t × t2) – (t × s) + (s2 × t2) + [s2 × (-s)]
= t3 – ts + s2t2 – s3
= t3 – st + s2t2 – s3
= t3 – st + s2t2 – s3

4. (a + b)(c – d) + (a – b)(c + d) + 2(ac + bd)
= a(c – d) + b(c – d) + a(c + d) – b(c + d) + 2(ac + bd)
= ac – ad + bc – bd + ac + ad – bc – bd + 2ac + 2bd
= ac + ac + 2ac = 4ac

5. (x + y)(2x + y) + (x + 2y)(x – y)
= x(2x + y) + y(2x + y) + x(x – y) + 2y(x – y)
= (x × 2x) + (x × y) + (y × 2x) + (y × y) + (x × x) – (x × y) + (2y × x) – (2y × y)
= 2x2 + xy + 2xy + y2 + x2 – xy + 2xy – 2y2
= (2x2 + x2) + (xy + 2xy – xy + 2xy) + (y2 – 2y2)
= 3x2 + 4xy – y2

6. (x + y)(x2 – xy + y2)
= x(x2 – xy + y2) + y(x2 – xy + y2)
= (x × x2) – (x × xy) + (x × y2) + (y × x2)
= x3 – x2y + xy2 + yx2 – xy2 + y3
= x3 + (-x2y + x2y) + yx2 – xy2 + y3
= x3 + (-x2y + x2y) + (xy2 – xy2) + y3
= x3 + (0 × x2y) + (0 × xy2) + y3
= x3 + 0 + 0 + y3 = x3 + y3

7. (1.5x – 4y)(1.5x + 4y + 3) – 4.5x + 12y
= 1.5x(1.5x + 4y + 3) – 4y(1.5x + 4y + 3) – 4.5x + 12y
= 2.25x2 + 6xy + 4.5x – 6xy – 16y2 – 12y – 4.5x + 12y
= 2.25x2 + (6 – 6)xy + (4.5 – 4.5)x – 16y2 + (12 – 12)y
= 2.25x2 + (0)xy + (0)x – 16y2 + (0)y
= 2.25x2 + 0 + 0 – 16y2 + 0
= 2.25x2 – 16y2

8. (a + b + c)(a + b – c)
= a(a + b – c) + b(a + b – c) + c(a + b – c)
= (a × a) + (a × b) – (a × c) + (b × a) + (b × b) – (b × c) + (c × a) + (c × b) – (c × c)
= a2 + ab – ac + ab + b2 – bc + ac + bc – c2
= a2 + (ab + ab) + (-ac + ac) + b2 + (-bc + bc) – c2
= a2 + (2ab) + (0) + b2 + 0 – c2
= a2 + 2ab + b2 – c2
= a2 + b2 – c2 + 2ab

Try These (Page 149)

Question 1.
Verify Identity (IV), for a = 2. b = 3, x = 5.
Solution:
We have
(x + a) (x + b) = x2 + (a + b)x + ab
Putting a = 2, b = 3 and x = 5 in the identity:
LHS = (x + a)(x + b)
= (5 + 2) (5 + 3)
= 7 × 8 = 56
RHS = x2 + (a + b)x + ab
= (5)2 + (2 + 3) × 5 + (2 × 3)
= 25 + (5) × 5 + 6
= 25 + 25 + 6 = 56
∴ LHS = RHS
∴ The given identity is true for the given values.

GSEB Solutions Class 8 Maths Chapter 9 Algebraic Expressions and Identities InText Questions

Question 2.
Consider the special case of Identity (IV) with a = b, what do you get? Is it related to Identity (I)?
Solution:
When a = b (each y)
(x + a) (x + b) = x2 + (a + b)x + ab becomes
(x + y)(x + y) = x2 + (y + y)x + (y × y)
= x2 +(2y)x + y2
= x2 + 2xy + y2
= Yes, it is the same as Identity I

Question 3.
Consider the special case of Identity (IV) with a = -c and b = -c. What do you get? Is it related to Identity (II)?
Solution:
Identity IV is given by
(x + a)(x + b) = x2 + (a + b)x + ab
Replacing ‘a’ by (-c) and ‘b’ by (-c), we have (x – c)(x – c)
= x2 + [(-c) + (-c)] x + [(-c) × (-c)]
= x2 + [-2c]x + (c2) = x2 – 2cx + c2

GSEB Solutions Class 8 Maths Chapter 9 Algebraic Expressions and Identities InText Questions

Question 4.
Consider the special case of Identity (IV) with b = -a. What do you get? It is related to Identity (III).
Solution:
The Identity IV is given by
(x + a)(x + b) = x2 + (a + b)x + ab
Replacing ‘b’ by (-a), we have:
(x + a)(x – a) = x2 + [a + (-a)]x + [a × (-a)]
= x2 + [0]x + [-a2]
= x2 + 0 + (-a2) = x2 – a2
which is same as the Identity III.

Leave a Comment

Your email address will not be published. Required fields are marked *