This GSEB Class 10 Maths Notes Chapter 2 Polynomials covers all the important topics and concepts as mentioned in the chapter.
Polynomials Class 10 GSEB Notes
An algebraic expression is a combination of terms connected by the operations of addition, subtraction, multiplication and division.
Polynomial
An algebraic expression of the form
p (x) = a0xn + a1xn-1 + a2xn-2 + ……….. + anx + an
where a0, a1, a2, ………….. an are real numbers provided a0 ≠ 0; n is non-negative integer is called a polynomial in x.
In simple words, an algebraic expression with more than one term is called a polynomial, provided it has no negative exponent for any variable in the terms.
Degree of Polynomial
The highest power of x in p (x) is called the degree of the polynomial p (x).
- A polynomial of degree 1 is called a linear polynomial.
- A polynomial of degree 2 is called a quadratic polynomial.
- A polynomial of degree 3 is called a cubic polynomial.
General form of Polynomial.
- ax + b; a ≠ 0 is linear polynomial.
- ax2 + bx + c; a ≠ 0, a, b, c are real numbers, is a quadratic polynomial.
- ax3 + bx2 + cx + d; a ≠ 0, a, b, c d are real numbers, is cubic polynomial.
Value of Polynomial
If p (x) is a polynomial in x, and if k is any real number, then the real number obtained by replacing x by k in p (x), is called the value of p (x) at x = k and is denoted by p (k).
Zero of Polynomial
A real number k is said to be a zero of a polynomial p (x) if p (k) = 0
In general, p (x) = ax + b
⇒ p (k) = ak + b
⇒ p (k) = 0
⇒ ak + b = 0
⇒ k = \(\frac{-b}{a}\)
It is clear that, zero of a linear polynomial is related to its coefficients.
![]()
Geometrical meaning of the zeroes of a Polynomial.
In general, for a linear polynomial ax + b, a ≠ 0, the graph of y = ax + b is a straight line with the x-axis at exactly one point, namely, (\(\frac{-b}{a}\), 0). Therefore, the linear polynomial ax + b, a ≠ 0, has exactly one zero, namely, the x-coordinate of the point where the graph of y = ax + b intersects the x-axis. For any quadratic polynomial ax2 + bx + c, a ≠ 0, the graph of the corresponding equation y = ax2 + bx + c has one of the two shapes either open upwards like this U or downwards like this ∩ depending on whether a > 0 or a < 0 respectively (These curves are called parabolas).
The zeroes of a quadratic polynomial ax2 + bx+c, a ≠ 0, are precisely the x-coordinates of the points where the parabola representing y = ax2 + bx + c intersects the x-axis.
The shape of the graph of y = ax2 + bx + c, the following three cases can happen:
Case (i): Here, the graph cuts the x-axis at two distinct points A and A’.
The x-coordinates of A and A’ are the two zeroes of the quadratic polynomial ax2 + bx + c in this case (see Figure I).
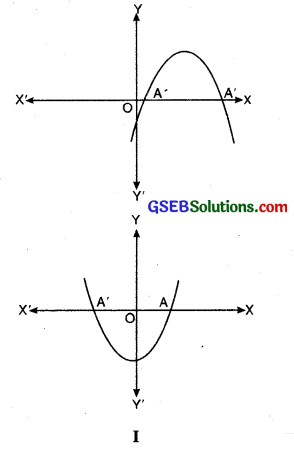
Case (ii): Here, the graph cuts the x-axis at exactly one point, i.e. at two coincident points. So, the two points A and A’ of Case (i) coincide here to become one point A (see Figure II).
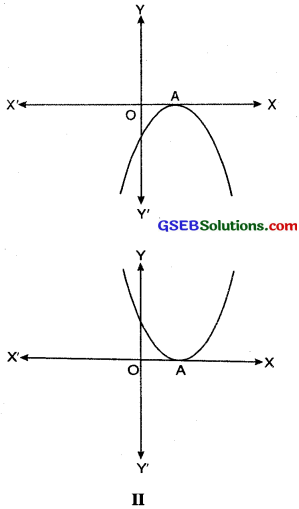
The x-coordinate of A is the only zero for the quadratic polynomial ax2 + bx + c in this case.
Case (iii): Here, the graph is either completely above the x-axis or completely below the x-axis. So, it does not cut the x-axis at any point (see Figure III).
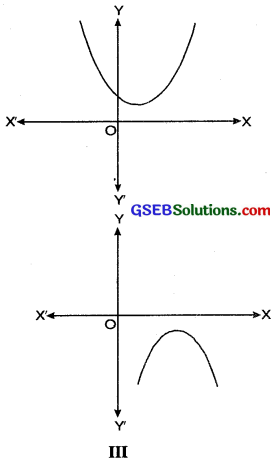
So, the quadratic polynomial ax2 + bx + c has no zero in this case.
Hence a quadratic polynomial can have either two distinct zeroes or two equal zeroes (i.e. one zero), or no zero. This also means that a polynomial of degree 2 has almost two zeroes.
In general, given a polynomial p (x) of degree n, the graph of y = p (x) intersects the x-axis at atmost n points. Therefore, a polynomial p (x) of degree n has atmost n zeroes.
Example:
Look at the graph in Figure IV given below. Each is the graph of y = p (x). where p (x) is a polynomial. For each of the graph, find the number of zeroes of p (x).
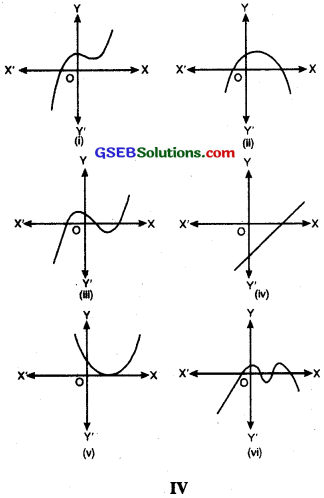
Solution:
(i) The number of zeroes is 1 as the graph intersects the x-axis at one point only.
(ii) The number of zeroes is 2 as the graph intersects the x-axis at two points.
(iii) The number of zeroes is 3 as the graph intersects the x-axis at three points
(iv) The number of zeroes is 1 as the graph intersects the x-axis at one point
(v) The number of zeroes is 1 as the graph intersect the x-axis at one point
(vi) The number of zeroes is 4 as the graph intersect the x-axis at four points.
Relationship Between Zeroes and Coefficients of a Polynomial.
In general, if α and β are the zeroes of the quadratic polynomial p (x) = ax2 + bx + c, a & 0, then we know that x – α and x – β are the factors of p (x). Therefore,
ax2 + bx + c = k (x – α) (x – β), where k is a constant
= k [x2 – (α + β) x + αβ]
= kx2 – k (α + β) x + k αβ
Comparing the coefficients of x2, x and constant terms on both the sides, we get
a = k, b = – k (α + β) and c = kαβ.
This gives α + β = \(\frac{-b}{a}\)
αβ = \(\frac{c}{a}\)
i.e. Sum of zeroes = α + β = \(\frac{-b}{a}\)
= \(-\frac{(\text { Coefficient of } x)}{\left(\text { Coefficient of } x^{2}\right)}\)
Product of zeroes = αβ = \(\frac{c}{a}\)
= \(\frac{\text { Constant Term }}{\text { Coefficient of } x^{2}}\)
In general, if α, β, γ are zeroes of the cubic polynomial ax3 + bx2 + cx + d then we know that x – α, x – β and x – γ are the factors of p (x). Therefore
ax3 + bx2 + cx + d = k (x – α) (x – β) (x – γ) where k is a constant.
= k [(x2 – (α + β) x + β) (x – γ)]
= k [x3 – (α + β + γ) x2 + (αβ + βy + γα) x – αβγ]
Comparing the coefficients of x3, x2, x and constant terms on both the sides, we get:
a = k, b = – k (α + β + γ), c = k (αβ + βγ + γα)
d = – kαβγ

Sum of the product of roots taken two at time
= αβ + βγ + γα = \(\frac{c}{a}\)
= \(\)
Product of roots = αβγ = \(\frac{-d}{a}\)
= \(\frac{-(\text { Constant term })}{\text { Coefficient of } x^{3}}\)
![]()
Division Algorithm For Polynomials
If p (x) and g (x) any two polynomials with g (x) ≠ 0, then we can find polynomials q (x) and r (x) such that:
p(x) = g (x) x q (x) + r (x) where r (x) = 0 or degree of r (x) < degree of g (x).
In simple words,
Dividend = Divisor × Quotient + Remainder
Note. If Remainder (i.e. r (x)) is equal to zero then Divisor (i.e. g (x)) is a factor of dividend (i.e. P (x))