GSEB Class 11 Statistics Notes Chapter 6 Permutations, Combinations and Binomial Expansion

This GSEB Class 11 Commerce Statistics Notes Chapter 6 Permutations, Combinations and Binomial Expansion covers all the important topics and concepts as mentioned in the chapter.

Permutations, Combinations and Binomial Expansion Class 11 GSEB Notes

Basic Principle of Counting:

• Basic Principle of Counting for Addition: If there are m distinct things in Group 1 and n distinct things in Group 2, then selection of one thing from total things of both groups can be done in m + n ways.
• Basic Principle of Counting for Multiplication: If the first operation can be done in m ways and corresponding to it second operation can be done in n ways, then two operations together can be done in m × n ways.
• General form of basic principle: If the first operation can be done in m ways, following which the second operation can be done in n ways and following which the third operation can be done in p ways then the total number of ways of occurrence of three operation together is m × n × p.

Meaning of Permutation:
If r distinct things out of given n distinct things are to arranged in r (1 ≤ r ≤ n) different places, then each such arrangement is called a permutation. The total number of such arrangements is denoted by ⁿp_r .ⁿp_r p(n, r)

• Order of the things is very important in permutation. AB and BA are two different permutations.
• ⁿP_r = n(n – 1) (n – 2) … (n – r + 1); 1 ≤ r ≤ n

Factorial:
The multiplication of numbers 1 to n, in their respective order, is called n factorial. It is denoted by n!.

• n! = n × (n – 1) × (n – 2)×… ×3 × 2 × 1
• 0! = 1 and 1! = 1

In factorial form: nPr = \(\frac{n !}{(n-r) !}\); n > 0, r ≥ 0, n ≥ r. n and r positive integers.

Some Results:
ⁿP₀ = 1, ⁿP_n = n !, ⁿP₁ = n, ⁿP_n-1 = n!

Permutations of identical things:
Prom n things, if p is the first type of identical things, q is the second type of identical things and r is the third type of indentical things then arrangement of n things are called permutations of identical objects.
Here, total number of permutation for n things = \(\frac{n !}{p ! q ! r !}\)

Meaning of Combination:
The total number of selection of r (r ≤ n) things out of n different things is called combination. It is denoted by ⁿC_r

• Here order is ignored. AB and BA are considered as same selection.
• ⁿC_r = \(\frac{n !}{r !(n-r) !}\)
• ⁿC₀ = 1; ⁿC_n = 1; ⁿC_r = ⁿC_n-r
  ⁿC₁ = n, ⁿC_n-1 = n
• If ⁿC_x = ⁿC_y, then x + y = n OR x = y.

Meaning of Binomial Expansion:

• Binomial Expression: Any expression consisting of two terms connected by + or – sign is called binomial expression.
• Binomial Expansion: The expansion of binomial expression (x + a) with positive integer power n is called binomial expansion, which is as follows:
• (x + a)ⁿ = ⁿC₀xⁿ + ⁿC₁x^n-1a + ⁿC₂x^n-2 a² + ⁿC₃ x^n-3 a³ + … + ⁿC_naⁿ
• General terms of binomial expansion is T_r+1 = ⁿCr x^n-r. a^r

Characteristic of Binomial Expansion:

• The total number of terms in binomial expansion is (n + 1).
• In successive terms of expansion, the power of x keeps reducing by one while power of a keeps increasing by one.
• In any term of expansion, the sum of power of x and a is n.
• The coefficients of successive terms of expansion are ⁿC₀, ⁿC₁, ⁿC₂…….. ⁿC_n.
• The coefficients of terms, placed equidistant from the midterm, are equal.

Important Results
1. Permutations:

• ⁿP_r = n(n- 1) (n-2)… (n-r + 1)
• ⁿP_r = \(\frac{n !}{(n-r) !}\)
• ⁿP_n = n !
• n ! = n(n- 1) (n-2) (n-3) … × 3 × 2 × 1
• Identical permutations :
  Total permutations of ‘n’ things = \(\frac{n !}{p ! q ! r !}\)

2. Combination:

• ⁿCr = \(\frac{n !}{r !(n-r) !}\)
• ⁿC₀ = 1, ⁿC₁ = n, ⁿC_n-1 = n
• ⁿC_n = 1
• ⁿC_r = ⁿC_n-r
• If ⁿCx = ⁿCy. then x + y = n or x = y
• ⁿC_r + ⁿC_r-1 = ⁿ⁺¹C_r
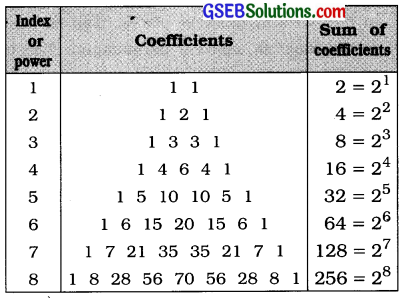
• ⁿC₀ + ⁿC₁ + … + ⁿC_n = 2ⁿ

3. Binomial expansion:

• (x + a)ⁿ = ⁿC₀xⁿ + ⁿC₁x^n-1a + ⁿC₂x^n-2a² + ⁿC3x^n-3a³ + … + ⁿCnaⁿ
• (x – a)ⁿ = ⁿC₀xⁿ – ⁿC₁x^n-1a + ⁿC₂x^n-2a² – ⁿC3x^n-3a³ + … ± ⁿCnaⁿ

4. General term of Binomial expansion:
General term = ⁿC_r x^n-r ar.
This term is (r + 1)th term of binomial expansion.

5. Some results:

• If n is even:
  The middle term of the expansion (x + a)ⁿ is obtained by putting r = \(\frac{n}{2}\) in the general term.
• If n is odd:
  Two middle terms of the expansion of (x + a)ⁿ is ⁿC₀ + ⁿC₁ + ⁿC₂ + ……… + ⁿC_n = 2ⁿ

6. Paseals triangle for coefficients of Binomial expansion: