This GSEB Class 12 Commerce Statistics Notes Part 2 Chapter 4 Limit Posting covers all the important topics and concepts as mentioned in the chapter.
Limit Class 12 GSEB Notes
Real Line and its Interval:
Real Line:
A line where its points are the real numbers, is called the real line.
Interval:
A set of reed numbers between any two real numbers is an interval.
1. Closed Interval: If a, be R and a < b, then the set of all real numbers between a and b including a and b is called a closed interval. It is denoted by [a, b]. Thus, [a, b] = (x|a ≤ x ≤ b, x ∈ R}.
2. Open Interval: If a, be R and a < b, then the set of all real numbers between a and b not including a and b is called an open interval. It is denoted by (a, b).
Thus, (a, b) = {x | a < x < b, x ∈ R}.
3. Closed-Open Interval: If a, b ∈ R and a < b, then the set of all real numbers between a and b including a but not including b is called a closed-open interval. It is denoted by la, b).
Thus, [a, b) = {x | a ≤ x < b, x ∈ R}.
4. Open-Closed Interval: If a, be R and a < b, then the set of all real numbers between a and b not including a but including b is called an open-closed interval. It is denoted by (a, b].
Thus, (a, b] = {x | a < x ≤ b, x ∈ R}. Modulus: If a real number is x, then modulus is used to express x as non-negative. The modulus of x is denoted by |x|. The modulus of real number is always positive.
|x| = x, if x > 0
= -x, if x < 0
Meaning of |x – a | < δ:
|x – a | < δ = (x – a) < δ if x ≥ a
or = x < (a + δ) if x ≥ a
= (a – x) < δ if x < a
or = x > (a – δ) if x < a
∴ |x – a| < δ ⇔ x ∈ (a- δ, a + δ)
![]()
Neighbourhood:
Any open interval containing a, a ∈ R is called a neighbourhood of a.
δ neighbourhood a:
If a ∈ R and δ is non-negative real number, then the open interval (a – δ, a + δ) is called δ neighbourhood of a. It is denoted by N (a, 5).
Thus, N (a, δ) = {x | (a – δ) < x < (a + δ), x ∈ R}
= {x| |x – a| < δ, x ∈ R}
In modulus form : N (a, 5) = |x – a| < δ
In interval form : N (a, 5) = (a – δ, a + δ)
Punctured δ neighbourhood of a:
If a ∈ R and δ is a non-negative real number, then the open interval (a – δ, a + δ)- {a} is called punctured δ neighbourhood of a. It is denoted by N* (a, δ). Thus,
N* (a, 8) = N (a, δ) – {a}
= {x | a – δ < x < a + δ; x ≠ a, x ∈ R}
= {x| |x – a| < δ; x ≠ a, x ∈ R}
Limit of a Function:
- Meaning of x → a: When the value of a variable x is brought very close to a number ‘a’ by increasing or decreasing its value, then it can be said that x tends to a. It is denoted by x → a.
- x → a means that value of x is very close to a but x ≠ a.
- Meaning of x → 0: If by decreasing the positive value of a variable x or by increasing the negative value of variable x, the value x is brought very close to ‘O’, then it can be said that x tends to ‘0’. It is denoted by x → 0.
- x → 0 means that the value of x is very close to ‘0’ but x ≠ 0.
Limit of a Function:
When the value of a variable x is brought closer and closer to a number ‘a’, the value of function fix) approaches closer and closer to a definite number T, then we can say that as x tends to ‘a’ f(x) tends to T that is x a,f (x) —> l. This definite number T is called limit of a function f(x). Symbolically it can be written as follows :
![]()
l is the limit of f(x). Hence, f(x) ≠ Z.
Important Formulae:
1. Working Rules of Limit:
If f(x) and g(x) are two functions of real variable x and

2. Standard Forms of Limit:
(1) If f(x) = a0 + a1x + a0x2 + … + anxn, then

3. δ neighbourhood of a :
N (a, δ) = (x| (a – δ) < x < (a + δ), x ∈ R}
4. Punctured 8 neighbourhood of a:
- N * (a, δ) = {x | (a – δ) < x < (a + δ), x ≠ a, x∈ R}
- N (a, δ) = |x – a|< δ (Modulus form)
- N (a, δ) = (a – δ, a + δ) (Interval form)
![]()
Remember to Find Limit of a Function
1. To find limit by Tabular Method :
| Limiting Value of x | Increasing Values | Decreasing Values |
| -2 | -2.1. -2.01, -2.001, -2.0001,… | – 1.9, – 1.99, -1.999, – 1.9999,… |
| – 1 | -1.1, -1.01, -1.001, -1.0001,… | -0.9, -0.99, -0.999, -0.9999,… |
| 0 | -0.1, -0.01, -0.001, -0.0001…. | 0.1, 0.01, 0.001, 0.0001,… |
| 1 | 0.9, 0.99, 0.999, 0.9999,… | 1.1, 1.01, 1.001, 1.0001,… |
| 2 | 1.9, 1.99, 1.999, 1.9999,… | 2.1, 2.01, 2.001, 2.0001,… |
2. To find limit by putting limiting value of x in function:
1. By putting the limiting value of x In the function f(x), if we get the numerator of f(x) as ‘0’, then the limit of function f(x) is ‘0’.
![]()
2. By putting the limiting value of x In the function f(x), if we get the denominator of f(x) as ‘0’. then the limit of function f(x) does not exist.
![]()
3. By putting the limiting value of x In the function f(x). if we get both the numerator and denominator of f(x) as 0 that Is we get \(\frac{0}{0}\) which is indeterminate. So we cannot find the value of limit of function f(x).
![]()
In such cases. we factorise numerator and denominator of function and find the limit of function after eliminating the common factor of function.
- If x → a. the common factor of the function will be (x – a).
- If x → – a, the common factor of the function will be (x + a).

4. Transforming the function to standard form of limit
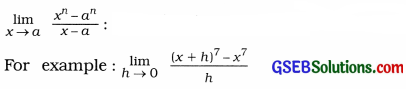
For transforming to standard form put x + h = t. So, when h → 0, t → x and h = t — x.
![]()