This GSEB Class 12 Commerce Statistics Notes Part 2 Chapter 5 Differentiation Posting covers all the important topics and concepts as mentioned in the chapter.
Differentiation Class 12 GSEB Notes
Differentiation and Derivative:
Differentiation:
A method of studying the rate of change in the dependent variable (function of independent variable) with respect to small change in the value of independent variable is called differentiation.
The process of obtaining derivative of a function is called differentiation.
Relative Change:
y = f(x). When the value of x changes from a to a + h, the value of f(x) will change from f(a) to f(a + h). Thus, for a change of h in the value of x, there is a change of f(a + h) – f(a) in the value of f(x). So, for change of h in the value of a, the relative change in the function will be \(\frac{f(a+h)-f(a)}{h}\)
Derivative: Let f: A → R and a e A; where, A is an open interval of R. If h is made very small and
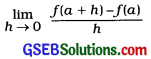
exists, then this limit of a function f is called derivative at x = a. It is denoted by f'(a).
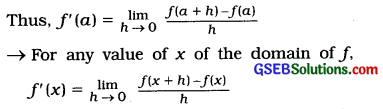
If y = f(x). then f’ (x) is denoted by \(\frac{d y}{d x}\)
Some Standard Derivatives:
The following standard derivatives are used to obtain the derivative of functions directly without using the definition of derivative:
- If y = xn, then \(\frac{d y}{d x}\) = n. xn-1
- If y = k, then \(\frac{d y}{d x}\) = 0; k = constant
Second Order Derivative: If y = f(x), then \(\frac{d y}{d x}\) = f'(x), is called first order derivative. The derivative of the first order derivative is called second order derivative. It is denoted by \(\frac{d^{2} y}{d x^{2}}\) OR f”(x).
Thus, \(\frac{d^{2} y}{d x^{2}}=\frac{d}{d x}\left[\frac{d y}{d x}\right]\)
Or
f”(x) = \(\frac{d}{d x}\)[f'(x)]
It is used for mlnhnisatlon of cost function, maximisation of revenue function and maximisation of profit function.
![]()
Increasing Function and Decreasing Function:
1. Increasing Function: y = f(x). If h is a very small positive number and f(a + h) >f(a) and f(a)<f(a-h), then at x = a, the function f(x) is called increasing function. That is, if at x = a, the function f(x) is increasing function then f(a) > 0.
2. Decreasing Function: y = fx). If h is a very small positive number and f(a + h) < f(a) and f(a) < f(a-h), then at x = a, the function f(x) is called decreasing function. That is, if at x = a, the function fix) is decreasing function then f(a) < 0.
Maximum and Minimum Values of a Function:
Maximum Value of a Function:
y = f(x). If h is a very small positive number and f(a) > f(a + h) and f(a) > f(a – h), then at x = a, the function f(x) is called maximum.
The conditions for maximisation of function at x = a:
- Necessary condition: f(a) = 0
- Sufficient condition: f”(a) < 0 (Negative)
Minimum Value of a Function:
y = f(x). If h is . a very small positive number and f(a) < f(a + h) and f(a) < f(a – h), then at x = a, the function f(x) is called minimum.
The condition for minimisation of function at x = a:
- Necessary condition: f(a) = 0
- Sufficient condition: f(a) > 0 (Positive)
Marginal Revenue and Marginal Cost:
Marginal Revenue:
The change in total revenue with respect to a small change in demand of an item is called marginal revenue.
- x = Demand of an item, p = Price of an item, then total revenue R = x . p
- Marginal revenue is obtained by finding derivative of R with respect to x.
Thus, marginal revenue = \(\frac{d \mathrm{R}}{d x}\)
Marginal Cost:
- The change in total cost with respect to a small change in production is called marginal cost.
- x = Production of an item, C = Production cost, then finding derivative of C with respect to x, marginal cost is obtained.
Thus, marginal cost = \(\frac{d \mathrm{C}}{d x}\)
Elasticity of Demand:
The ratio of percentage change in demand and the percentage change in price is called elasticity of demand. Thus,
Elasticity of demand = \(=-\frac{\text { Percentage change in demand }}{\text { Percentage change in price }}\)
- The demand of an item x is a function of the price of an item p, i.e., x = f(p).
- The relation between demand of an item and its price is inverse. Hence, the negative sign is taken in the formula of elasticity of demand.
- Demand x is a function of price p. Hence, taking the derivative of x with respect to p the elasticity of demand is obtained as follows: Elasticity of demand = \(-\frac{p}{x} \cdot \frac{d x}{d p}\)
Minimisation of Cost:
x = Units of production, C = Production cost. The conditions for minimisation of cost are as follows:
- Necessary condition: \(\frac{d \mathrm{C}}{d x}\) = 0
- Sufficient condition: \(\frac{d^{2} \mathrm{C}}{d x^{2}}\) > 0 (Positive)
Maximisation of Revenue:
x Demand of an item, p = Price per unit of an item, Revenue R = x . p.
The conditions for maximisation of revenue are as follows:
- Necessary condition: \(\frac{d \mathrm{R}}{d x}\) = 0
- Sufficient condition: \(\frac{d^{2} \mathrm{R}}{d x^{2}}\) < 0 (Negative)
![]()
Maximisation of Profit:
If R = Total revenue, C = Total production cost, then profit P = R – C.
The conditions for maximisation of profit are as follows:
- Necessary condition: \(\frac{d \mathrm{P}}{d x}\) = 0
- Sufficient condition: \(\frac{d^{2} \mathrm{P}}{d x^{2}}\) < 0 (Negative)
Stationary Points of a Function:
y = f(x). Points at which the maximum and minimum values of f(x) are obtained are called the stationary points of function.
Necessary condition for stationary points: f'(x) = 0
Important Formulae:
1. Derivative:
By Definition:
y = f(x).
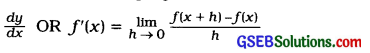
By standard Forms:
- y = f(x) = xn \(\frac{d y}{d x}\)OR f'(x) = nxn-1
- y = f(x) = k; \(\frac{d y}{d x}\) OR f'(x) = o
Where, k = constant
2. Rules for Differentiation: u and y are differentiable functions of x.
- Rule of additIon – subtraction:
If y = u ± v, then \(\frac{d y}{d x}=\frac{d u}{d x} \pm \frac{d v}{d x}\) - Rule of multiplication:
If y = u . u. then \(\frac{d y}{d x}=u \cdot \frac{d v}{d x}+v \cdot \frac{d u}{d x}\) - Rule of Division:
If y = \(\frac{u}{v}\); u ≠ 0. then \(\frac{d y}{d x}=\frac{v \cdot \frac{d u}{d x}-u \cdot \frac{d v}{d x}}{v^{2}}\) - Chain Rule: If y is a function of u and u is a function of x, then \(\frac{d y}{d x}=\frac{d y}{d u} \cdot \frac{d u}{d x}\)
3. Increasing and Decreasing Function:
- At x = a, for increasing function f'(a) > 0
- At x = a, for decreasing function f'(a) < 0
4. Conditions for maximum value of a function:
For the function f(x) to be maximum at x = a
- Necessary condition: f'(a) = 0
- Sufficient condition: f”(a) < 0 (Negative)
5. Conditions for minimum value of a function:
For the function f(x) to be minimum at x = a
- Necessary condition: f'(a) = 0
- Sufficient condition: f”(a) > 0 (Positive)
6. Marginal Revenue = \(\frac{d \mathrm{R}}{d x}\)
R = x .p, x = Demand, p = Price
7. Marginal cost = \(\frac{d \mathrm{C}}{d x}\)
C = Production cost, x = Production
8. Elasticity of demand = \(-\frac{p}{x} \cdot \frac{d x}{d p}\)
p = Price, x = Demand
9. Conditions for Minimum Cost:
- Necessary condition: \(\frac{d \mathrm{C}}{d x}\) = 0
- Sufficient condition: \(\frac{d^{2} \mathrm{C}}{d x^{2}}\) > 0
Where, C = Production cost, x = Production
10. Conditions for Maximum Revenue:
- Necessary condition: \(\frac{d \mathrm{R}}{d x}\) = 0
- Sufficient condition: \(\frac{d^{2} \mathrm{R}}{d x^{2}}\) < 0
Where, R = xp; x = Demand, p = Price
11. Conditions for Maximum Profit:
- Necessary condition \(\frac{d \mathrm{P}}{d x}\) = 0
- Sufficient condition: \(\frac{d^{2} \mathrm{P}}{d x^{2}}\) < 0
Where, P = R – C; P = Profit, R = Total revenue, C = Total cost ,
12. The necessary condition for stationary points of a function:
\(\frac{d y}{d x}\) = 0 OR f'(x) = 0
![]()
Remember for Derivative of Function
| 1. y = xn | \(\frac{d y}{d x}\) = n. xn-1 |
| 2. y = x | \(\frac{d y}{d x}\) = 1 |
| 3. y = x2 | \(\frac{d y}{d x}\) = 2x |
| 4. y = x3 | \(\frac{d y}{d x}\) = 3x2 |
| 5. y = c | \(\frac{d y}{d x}\) = 0, c = constant |
| 6. y = ax | \(\frac{d y}{d x}\) = a, a = constant |
| 7. y = \(\frac{1}{x}\) | \( \frac{d y}{d x}=-\frac{1}{x^{2}} \), c = constant |
| 8. y = \(\frac{c}{x}\) | \( \frac{d y}{d x}=-\frac{c}{x^{2}} \); c = constant |
| 9. y = \(\frac{c}{a x-b}\) | \( \frac{d y}{d x}=-\frac{a c}{(a x-b)^{2}} \); a, b, c = constant |
| 10. y = \(\frac{c}{a-bx}\) | \( \frac{d y}{d x}=\frac{b c}{(a-b x)^{2}} \); a, b, c = constant |
| 11. y = \(\frac{c}{z}\) | \( \frac{d y}{d z}=-\frac{c}{z^{2}} \); c = constant |