This GSEB Class 6 Maths Notes Chapter 12 Ratio and Proportion covers all the important topics and concepts as mentioned in the chapter.
Ratio and Proportion Class 6 GSEB Notes
Introduction:
In our daily life, many a times we compare two quantities of the same type. For example, In an examination Atulya got 90 marks and Mohit got 80 marks.
Their performance can be compared in two ways :
1. Comparison by difference:
Difference of marks = 90 – 80 = 10.
i.e., Atulya got 10 marks more than Mohit.
Such a comparison is known as com-parison by difference.
2. Comparison by division.
\(\frac{\text { Atulya got marks }}{\text { Mohit got marks }}=\frac{90}{80}=\frac{9}{8}\)
Atulya’s marks are \(\frac{9}{8}\) times the marks 8 of Mohit. Such a comparison is known as comparison by division.
Ratio:
When we compare two quantities of the same kind by division, we say that we have formed a ratio of the two quantities.
We can say that ratio of breadth of two copies is 40 ÷ 30 or \(\frac{40}{30}\).
- The symbol ‘:’ is used to express a ratio. So the above ratio is written as 40 : 30 and is read as ‘40 is to 30’ or ‘40 to 30’.
- In general, the ratio of two numbers (measures/magnitudes) a and b (b ≠ c) is and is denoted a : b, a and b are called the terms of the ratio.
- The first term of a ratio is called the antecedent and the second term is called the consequent.
Note: The word ‘antecedent’ literally means ‘that which goes before’.
The word ‘consequent’ literally means ‘that which goes after’. In the ratio 3 : 5, 3 is the antecedent and 5 is the consequent.
Remark:
- A ratio is always expressed in the simplest form.
- To express a ratio in its simplest form, we need to convert the two quantities to same units and to find the H.C.F. of both quantities and then factorizing the two quantities in two factors in’ such a manner that one factor is the H.C.F. and then cancelling it, we get the required ratio in the simplest form.
![]()
Proportion
Proportion (Samanupat). An equality of two ratios is called a proportion.
The numbers a, b,c,d are in proportion if the ratio of the first two is equal to the ratio of the last two, i.e.,
a : b = c : d or a : b :: c : d
This is read as ‘a is to b as c is to d ‘or’ a to b as c to d.
a, b, c and d are the I, II, III and IV terms of a proportion.
I and IV terms of a proportion are called Extreme Terms or Extremes.
II and III terms are called the Middle terms or Means.
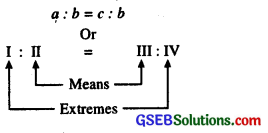
Moreover, if the four numbers are in proportion, then the product of the extremes is equal to the product of the means.
In other words :
If a : b = c : d
then, ad = bc
Note:
- If ad = be, then a, b, c, d are in proportion and if ad ≠ be, then a,b,c,d are not in proportion.
- If a : b = b : c, then a,b,c are in proportion.
Mean Proportion:
If the middle terms are repeated then each of the middle terms is called the mean proportion.
i.e., a : b = b : c or b 2 = ac
b is called the mean proportion of a and c.
Remark. From the terms of given proportion, we can make three more proportions.
Unitary Method:
The method of finding first the value of one (unit) quantity from the value of the given quantities and then the value of the required quantities is called the Unitary Method.
Direct Variation:
If the value of one quantity increases or (decreases), the value of the other quantity also increases (or decreases) in such a manner that the ratio of the values of the two quantities remains the same. The two quantities are said to be in Direct Variation.