This GSEB Class 6 Maths Notes Chapter 2 Whole Numbers covers all the important topics and concepts as mentioned in the chapter.
Whole Numbers Class 6 GSEB Notes
Natural Numbers:
The counting numbers 1, 2, 3, 4, are called Natural Numbers.
Natural numbers are represented by ‘N’ Thus N = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11,….}
Facts about Natural Numbers
- The smallest natural number is ‘1’.
- Any natural number (except 1) can be obtained by adding ‘1’ to its predecessor.
- The successor of a natural number is 1 more than the natural number.
- 1 is not the successor of any natural number.
- There is no predecessor of ‘ 1’ in natural numbers.
Whole Numbers:
- The number ‘0’ together with the natural numbers 1, 2, 3, 4,………… are called whole numbers.
- Whole numbers are represented by ‘W’
Thus W = {0, 1, 2, 3, 4, 5, 6, …. }
Facts about Whole Numbers
- ‘0’ is the smallest whole number.
- There is no largest whole number.
- Every natural number is a whole number but ‘O’ is a whole number which is not a natural number.
- There is no predecessor of ‘0’ in whole numbers.
![]()
Successor and Predecessor of a Whole Number
Successor:
- The successor of a whole number is the number obtained by adding 1 to it. Clearly the successor of 0 is 1 ; successor of 1 is 2, successor of 2 is 3 and so on
- Every whole number has successor.
Predecessor:
- The predecessor of a whole number is one less than the given number. Clearly the predecessor of 2 is 1, Predecessor of 1 is 0.
- But 0 does not have any predecessor in whole numbers. Every whole number other than zero has predecessor.
Representation of Whole Numbers on Number Line
To represent whole numbers on a number line,
1. Draw a line and matic any point O on it.
2. Starting from O, mark points A, B, C on the line at equal steps to the right of O.
im-1
3. Label the point O as O (Zero).
Let OA = 1 unit
Then, OB = OA + AB = 1 + 1 = 2 units
OC = OB + BC = 2+ 1 = 3 units and so on.
Thus the points O, A, B, C, D, E correspond to the whole numbers 0, 1, 2, 3, 4, 5 respectively.
Counting in the same manner, we can represent every whole number by some point on the line, called number line.
Looking at the above number line of whole numbers we observe that
- No whole number is on the left of zero (‘0’) and every whole number on right of ‘0’ is greater than 0.
- A whole number on the right of given whole number is greater than the given whole number. e.g : 8 > 3, 9 > 6, and so on.
- A whole number on the left of given whole number (except 0) is less than the given whole number, e.g: 2 < 8, 5 < 9 and so on.
Number Line can be drawn in vertical form also.
Addition of Whole Numbers on Number Line:
In order to add two whole numbers on the number line, we follow the following steps :
- Draw a number line and mark whole numbers on it.
- Mark the first given number on the number line.
- Move as many units as the second number to the right of the first number.
- The number obtained in step 3 represents the sum of two whole numbers.
- Similarly, sum of three, four and five whole numbers can be found out.
![]()
Subtraction of Whole Numbers on Number Line
In order to subtract one whole number from another whole number on number line, we follow the following steps:
- Draw a number line and mark whole number on it.
- Mark the first given number on the number line.
- Starting from first number move as many units as the second number to the left of first number.
- The number obtained in step 3 represents the required difference of the given whole numbers on the number line.
Product of Whole Numbers on Number Line on number line, following steps are followed:
- Draw a number line and mark whole numbers on it.
- Starting from 0, we move to the right of 0 and count the units same as second number and it is considered as one jump.
- Similar jumps are made equal to first number to reach at final point.
- The final number represent the product of two whole numbers.
Division on Number Line
For division of two whole numbers, following steps are followed :
- Draw a number line and mark whole numbers on it.
- Starting from 0 we move to the right of 0 and reached at first number.
- From First number we jumps towards zero taking one jump value equal to second number.
- The number of jumps taken to reach at zero is quotient.
Properties of Whole Numbers, Operations on Whole Numbers, Properties of Addition:
- Closure Property: If a and b are any two whole numbers then a + b is also a whole number.
- Commutative Property: If a and b are any two whole numbers then a + b – b + a.
- Associative Property: If a, b, c are any three whole numbers then (a + b) + c = a + (jb + c).
- Additive Property of Zero: If a is any whole number then, a + 0 = 0 + a = a
Here 0 is called an Identity element for addition.
Properties of Subtraction
- If a and b are two whole numbers such that a > b or a = b, then a – b is a whole number, otherwise subtraction is not possible in whole numbers,
- If a and b are two whole numbers, then generally a – b ≠ b – a.
- If a is any whole number then a – 0 = a but 0 – a is not defined.
- If a, by c are three whole numbers then generally (a – b) – c ≠ a – (b – c).
Properties of Multiplication
- Closure Property: If a and b are any two whole numbers then a × b is also a whole number.
- Commutative Property: If a and b are any two whole numbers then a × b = b × a.
- Multiplicative Property of 0: If a is any whole number then o × 0 = 0 × a =0
- Multiplicative Property of 1. If a is any whole number then a × 1 = 1 × a = a.
- Associative Property. If a, b, c are any whole numbers then (a × b) × c = a × (b × c).
- Distributive Property of Multiplica-tion over Addition. If a, b, c are any three whole numbers then a × (b + c) = a × b + a × c.
- Distributive Property of Multiplica-tion over Subtraction. If a, b, c are any three whole numbers then a × (b – c) = a × b – a × c.
- If a, b, c are any three whole numbers such that a > b and c ≠ 0 then a × c > b × c.
![]()
Properties of Division
- If a and b (b * 0) are whole numbers, then a -s- b is not necessarily a whole number.
- Division by zero is undefined.
- If a is a whole number then a ÷ a = 1.
- If a is a whole number then a + 1 = a.
- If a is a whole number then 0 ÷ a = 0.
- Division Algorithm. Dividend = (Divisor × Quotient) + Remainder.
Patterns in Whole Numbers
We shall try to arrange numbers in elementary shapes made up of dots. The shapes we take are (1) a line (2) a rectangle (3) a square and (4) a triangle. Every number should be arranged in one of these shapes. No other shape is allowed.
1. Representing whole numbers by line segments
If ‘•’ represents 1, then 2, 3, 4, 5,…….can be represented by line segments as follow:

2. Representing whole numbers by triangles:
Whole numbers can be represented by triangles. Such numbers are called triangular numbers. 1, 3, 6, 10, 15 are some triangular numbers.
Let ‘•’ represent
1. Following table shows the representation of whole numbers by triangles.
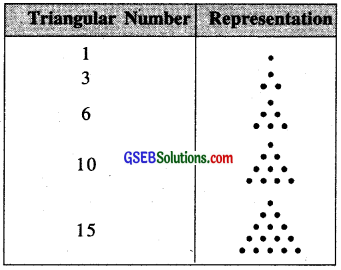
1 is both triangular and square number.
3. Representing whole numbers by squares Some whole number can be represented by squares 1, 4, 9, 16, 25, etc. are square numbers.

4. Representing whole numbers by rectangle
Some whole numbers can be represented by rectangles 6, 8, 10 … are rectangular numbers.

Some numbers can be shown by two rectangles, for example,

Patterns Observations
Observation of patterns can guide you in simplifying the process. Study the following:
(a) 325 + 9 = 325 + 10 – 1
= 335 – 1 = 334
(b) 325 – 9 = 325 – 10 +1
= 315 + 1 = 316
(c) 325 + 99 = 325 + 100 – 1
= 425 – 1 =424
(d) 325 – 99 = 325 – 100 + 1
= 225 + 1 = 226
Here is one more pattern.
(a) 84 × 9 = 84 × (10 – 1)
= 840 – 84 = 756
(b) 84 × 99 = 84 × (100 – 1)
= 8400 – 84 = 8316
(c) 96 × 125 = 96 × \(\frac{1000}{8}\)
= \(\frac{96000}{8}\) = 12000