This GSEB Class 7 Maths Notes Chapter 5 Lines and Angles covers all the important topics and concepts as mentioned in the chapter.
Lines and Angles Class 7 GSEB Notes
1. Line: A line can be defined as a set of continuous points that has an indefinite length. It has no thickness. It can be extended endlessly in both the directions.
It is denoted by \(\overleftrightarrow{\mathrm{AB}}\).
![]()
2. Ray: A ray can be defined as part of a line that has a fixed starting point but no end point. It can be extended infinitely in one direction. It is denoted by \(.\overrightarrow{A B}\)..
![]()
3. Line segment: A line segment is a part of a line that has two end points and a fixed length. It can’t be extended in any
direction. It is denoted by \(\overline{\mathrm{AB}}\).
![]()
Angles and its Types
Angle: An angle is formed by two rays having common starting initial point. Rays form the arms of the angle and the common point is called the vertex. Angle is measured in degrees (°) using a protractor. It is denoted by the the symbol ∠.
In the figure the common point O is the vertex and the rays OA and OB are the arms of the angle AOB.

In general angle AOB is denoted by ∠AOB or ∠BOA.
Types of Angles
1. Zero angle: An angle whose measure is 0° is called a zero angle. When two arms of an angle lie on each other, 0° angle is formed. In figure, ∠AOB = 0°.
∴ ∠AOB is zero angle.

2. Acute angle: An angle that measures between 0° and 90° (0° < acute angle < 90°) is called an acute angle. In figure, ∠AOB = 45° (<90°) (0° < ∠AOB < 90°).

∴ ∠AOB is an acute angle.
3. Right angle: An angle whose measure is 90° is called a right angle. The rays making a right angle are also called perpendicular rays. In figure, ∠AOB = 90°
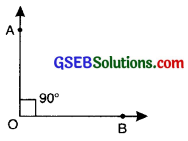
∴ ∠AOB is a right angle.
4. Obtuse angle: An angle whose measure lies between 90° and 180° is called an obtuse angle. In given figure,
∠AOB = 120° (90° < ∠AOB < 180°)
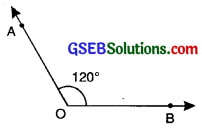
∴ ∠AOB is an obtuse angle.
5. Straight angle: An angle that measures 180° is called a straight angle. It is called so as the two rays form a straight line.
In figure, ∠AOB = 180°.

∴ ∠AOB is a straight angle.
6. Reflex angle: An angle whose measure lies between 180° and 360° is called a reflex angle.
In given figure, Reflex ZPOR = 320° (180° < reflex ∠POR < 360°)
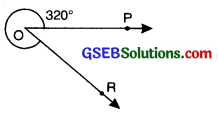
7. Complete angle: An angle whose measure is exactly 360° is called a complete angle. It forms a complete circle. In figure, ∠POR = 360°
∴ ∠POR is a complete angle.
![]()
More about angles:
(i) Complementary angles: When the sun of measure of two angles is 90° then these angles are called complementary angles.
For example, 70° + 20° = 90°, then 70° and 20° are complementary to each other.
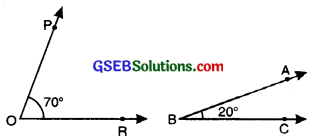
In given figure,
∠POR + ∠ABC = 70° + 20° = 90°
∠POR and ∠ABC are complementary angles and
∠POR is complement of ∠ABC and vice versa.
(II) Supplementary angles: When the sum of measure of two angles is 180° then these angles are called supplementary angles. For example, 80° + 100° = 180°, then 80° and 100° are supplementary to each other.
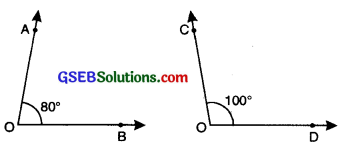
In the given figure.
∠AOB + ∠COD = 80° + 100°
= 180°
∠AOB and ∠COD are supplementary angles and ∠AOB is called the supplement of ∠COD and vice versa.
(III) Adjacent angles: Two angles are said to be adjacent angles if:
(a) They have a common arm
(b) They have a common vertex
(c) Non-Common arms lie on either side of common arm.
In fig. ∠XOY and ∠YOZ are adjacent angles with common vertex O having OY as common arm. OX and OZ as non common arms lying on either side of OY.

(IV) Linear pair: Two adjacent angles whose sum is 180° are said to form a linear pair. In figure ZAOC + ZCOB = 180°
∴ These angles form a linear pair.

The angles in a linear pair are supplementary i.e., sum of angles is 180°.
(V) Vertically Opposite Angles: When two straight lines intersect each other, four angles are formed.
The pair of angles which lie on the opposite side of the point of intersection are called vertically opposite angles.
In the adjoining figure straight lines \(\overleftrightarrow{\mathrm{AB}}\) and \(\overleftrightarrow{\mathrm{CD}}\) intersect each other at point O. ZAOD and ZBOC form one pair of vertically opposite angles, ∠AOC and ∠BOD form another pair of vertically opposite angles.
Vertically opposite angles are always equal.
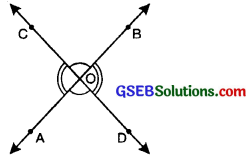
i.e., ∠AOD = ∠BOC
∠AOC = ∠BOD
Pairs of Lines:
1. Intersecting lines: When two lines intersect exactly at one point, they are called intersecting lines. In figure, AB and CD are intersecting lines and O is the point of intersection.

2. Perpendicular lines: Two lines are said to be perpendicular to each other if they meet or intersect at a right angle. In figure, CD is perpendicular to AB and is written as CD 1 AB.
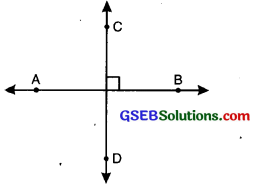
3. Parallel lines: Two lines in the same plane are said to be parallel if they are at an equal distance from each other throughout and never meet.
In the given figure, line l and m are parallel to each other. It is represented as l ∥ m.
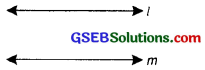
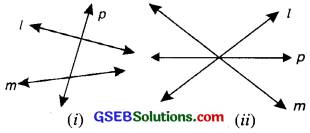
4. Transversal: A transversal is a line that intersects two or more lines in the same plane at distinct points. The lines may or may not be parallel.
In Fig (i) transversal p intersects two lines l and m. In Fig. (ii) the line p intersects the lines l and m, but it is not transversal, because line p does not intersect two lines l and m in two distinct points.
Angles made by a Transversal (With Non-Parallel Lines):
In figure, you see lines l and m cut by transversal p. The eight angles marked 1 to 8 have their special names. These angles can be classified as follows:
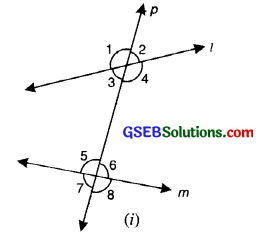
1. Interior angles:
∠3, ∠4
∠5, ∠6
2. Exterior angles:
∠1, ∠2
∠7, ∠8
3. Pairs of corresponding angles:
∠1, ∠5,
∠2, ∠6,
∠3, ∠7,
∠4, ∠8,
4. Pairs of alternate interior angles :
∠3, ∠6,
∠4, ∠5,
5. Pairs of alternate exterior angles
∠1, ∠8
∠2, ∠7
6. Pairs of interior angles on the same side of the transversal also called co-interior angles:
∠3, ∠5
∠4, ∠6
![]()
Transversal of parallel lines: The relation between the angles made by a transversal with two Parallel lines gives rise to quite interesting results.
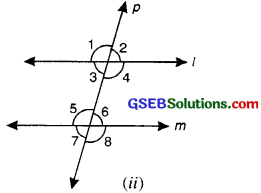
1. If two parallel lines are cut by a transversal. All the pairs of corresponding angles are equal in measure.
i.e.∠1 = ∠5,
∠2 = ∠6,
∠3 = ∠1,
∠4 = ∠8
2. If two parallel lines are cut by a transversal, all pairs of alternative interior angles are qual:
i.e.∠3 = ∠6 and ∠4 = ∠5
3. If two parallel lines are cut by a transversal, both the pairs of alternate exterior angles are equal
i.e. ∠1 = ∠8 and ∠2 = ∠1
4. If two parallel lines are cut by a transversal then both pair of interior angles on the same side of the trasversal or co-interior angles are supplementary i.e. ∠4 + ∠6 = 180° and ∠3 + ∠5 = 180°