This GSEB Class 8 Maths Notes Chapter 9 Algebraic Expressions and Identities covers all the important topics and concepts as mentioned in the chapter.
Algebraic Expressions and Identities Class 8 GSEB Notes
→ Algebraic expressions are formed from variables and constants.
→ Constant is a symbol which has a fixed numerical value, such as -5, 7, etc.
→ A variable / literal is a symbol which does not have a fixed numerical value. In general, we use alphabets to represent variables.
→ In an algebraic expression, one or more signs separates it into several parts. Each part along with its sign is known as a term.
→ A polynomial with a single term is called a monomial.
e.g. 5x, -8y, 47, -105
→ A polynomial with two terms is called a binomial.
e.g. 3x + 2, – 12x + 1, 6-x, -7x-2y
→ A polynomial with three terms is called a trinomial.
e.g. 2x2 – 3x + 1, 8 – 4x3 + 9x2,
16x2 + 40xy + 25y2
→ An expression containing one or more terms with non-zero coefficient is called a polynomial.
→ The terms which have the same variables with the same powers are called like terms, e.g. -5x2 and 7x2; 6xy2z and -8xy2z
→ The terms which do not have the same variable are called unlike terms.
e.g. 3x and 5y; – 4×2 and -3xy; – 7x and 2y2
![]()
→ Product of a monomial and a monomial: For the product of two monomials, their respective coefficients and their respective powers of the variables are multiplied.
→The product of two monomials is always a monomial.
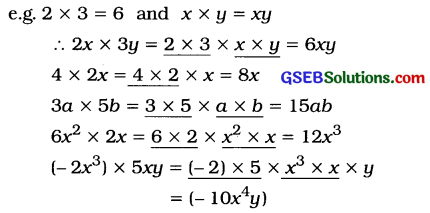
→ The product of a monomial and a binomial:
We have learned the distribution of multiplication over addition, x × (y + z) = (x × y) + (x × z) = xy + xz
![]()
→ The distributive property is used as below: 2x × (3a + 5b) = (2x × 3a) + (2x × 5b)
= 6xa + 10xb
Thus, using the distributive property, the product given on the left side is expressed as the addition on the right side. This process is called expansion.
→ Identity: An equality which holds true for any value of the variables in it, is called an identity.
→ Identities:
- (a + b)2 = a2 + 2ab + b2
- (a – b)2 = a2 – 2ab + b2
- (a + b) (a – b) = a2 – b2
- (x + a) (x + b) = x2 + (a + b)x + ab