GSEB Class 9 Maths Notes Chapter 13 પૃષ્ઠફળ અને ઘનફળ

This GSEB Class 9 Maths Notes Chapter 13 પૃષ્ઠફળ અને ઘનફળ covers all the important topics and concepts as mentioned in the chapter.

પૃષ્ઠફળ અને ઘનફળ Class 9 GSEB Notes

→ લંબઘન (cuboid) અને સમઘન(cube)નાં પૃષ્ઠફળઃ ઘણા બધા સમાન આકાર અને કદના લંબચોરસ કાગળના પૂંઠામાંથી કાપી અને તેની લંબરૂપે થપ્પી કરવાથી લંબઘન મળે. લંબઘન એ છે લંબચોરસ પ્રદેશવાળા પૃષ્ઠ(સપાટી)થી બનેલો ઘન પદાર્થ છે.

→ લંબઘનનું પૃષ્ઠફળ = 2 (lb + bh + hl); જ્યાં l, b અને h લંબઘનની ત્રણ ધાર (Edges) છે. બીજા શબ્દોમાં l, b અને h અનુક્રમે લંબઘનની લંબાઈ, પહોળાઈ અને ઊંચાઈ છે.

→ જે લંબઘનમાં લંબાઈ, પહોળાઈ અને ઊંચાઈ સમાન હોય તે લંબઘનને સમઘન કહેવાય.

→ a ધારવાળા સમઘનનું પૃષ્ઠફળ = 6a²

→ લંબઘન તથા સમઘનમાં પાયા અને મથાળા સિવાયનાં ચાર પૃષ્ઠોને પાર્થપૃષ્ઠો (Lateral Surfaces) કહેવાય છે.

→ લંબઘનનાં પાર્શ્વપૃષ્ઠોનું ક્ષેત્રફળ = 2h (l + b)
= ઊંચાઈ × પાયાની પરિમિતિ

→ સમઘનનાં પાર્થપૃષ્ઠોનું ક્ષેત્રફળ = 4a²

→ 1 મી = 10,000 સેમી²

→ 1 હેક્ટર = 10,000 મી²

ઉદાહરણ : 1.
એક લંબઘનની લંબાઈ, પહોળાઈ અને ઊંચાઈ અનુક્રમે 25 સેમી, 20 સેમી અને 10 સેમી છે, તો તેનું કુલ પૃષ્ઠફળ શોધો.
ઉત્તર:
આપેલ લંબઘન માટે લંબાઈ = 25 સેમી, પહોળાઈ b = 20 સેમી અને ઊંચાઈ h = 10 સેમી.
લંબઘનનું કુલ પૃષ્ઠફળ = 2 (lb + bh + hl)
= 2 (25 × 20 + 20 × 10 + 10 × 25) સેમી²
= 2 (500 + 200 + 250) સેમી²
= 2 (950) સેમી²
= 1900 સેમી²

ઉદાહરણ : 2.
એક સમઘનની ધાર 16 સેમી છે, તો તેનું પૃષ્ઠફળ શોધો.
ઉત્તર:
આપેલ સમઘન માટે ધાર વ = 16 સેમી
સમઘનનું પૃષ્ઠફળ = 6a²
= 6 (16)² સેમી²
= 6 × 256 સેમી²
= 1536 સેમી²

ઉદાહરણ : ૩.
પતરાંની બે પેટી છે. લંબઘન પેટીની લંબાઈ, પહોળાઈ અને ઊંચાઈ અનુક્રમે 30 સેમી, 25 સેમી અને 20 સેમી છે, જ્યારે સમઘન પેટીની ધાર 25 સેમી છે. કઈ પેટી બનાવવામાં કેટલા સેમી પતરું વધારે વપરાય તે શોધો.
ઉત્તર:
લંબઘન પેટી માટે લંબાઈ l = 30 સેમી, પહોળાઈ b = 25 સેમી અને ઊંચાઈ h = 20 સેમી.
સમઘન પેટીની ધાર a = 25 સેમી

લંબઘન પેટીમાં વપરાતા પતરાંનું ક્ષેત્રફળ
= લંબઘનનું પૃષ્ઠફળ
= 2 (lb + bh + hl)
= 2 (30 × 25 + 25 × 20 + 20 × 30) સેમી²
= 2 (750 + 500 + 600) સેમી²
= 2 (1850) સેમી²
= 3700 સેમી²

સમઘન પેટીમાં વપરાતા પતરાંનું ક્ષેત્રફળ = સમઘનનું પૃષ્ઠફળ
= 6a²
= 6 (25)² સેમી²
= 6 (625) સેમી²
= 3750 સેમી²
આમ, સમઘન પેટીમાં 3750 સેમી² પતરું અને લંબઘન પેટીમાં 3700 સેમી² પતરું વપરાય.
આથી સમઘન પેટી બનાવવામાં 3750 – 3700 = 50 સેમી² પતરું વધારે વપરાય.

ઉદાહરણ : 4.
એક લંબઘન ટાંકી 2 મી લાંબી, 1 મી પહોળી અને 80 સેમી ઊંચી છે. તેની તળિયા સિવાયની બાકીની પાંચ સપાટીઓ પર 20 સેમી × 20 સેમીના ટાઈલ્સ જડવાના છે, તો કેટલા ટાઇલ્સ જોઈશે તે શોધો.
ઉત્તર:
લંબઘન ટાંકી માટે લંબાઈ l = 2 મી = 200 સેમી, પહોળાઈ b = 1 મી = 100 સેમી અને ઊંચાઈ h = 80 સેમી. જે સપાટીઓ પર ટાઇલ્સ જડવાના છે તે પૈકી બે સપાટીઓ લંબાઈ અને ઊંચાઈથી, બે સપાટીએ પહોળાઈ અને ઊંચાઈથી તથા એક સપાટી લંબાઈ અને પહોળાઈથી સીમિત થાય. એક ચોરસ ટાઇલનું ક્ષેત્રફળ = 20 × 20 સેમી²

લંબાઈ અને ઊંચાઈથી સીમિત સપાટીનું ક્ષેત્રફળ
= 200 × 80 સેમી²

પહોળાઈ અને ઊંચાઈથી સીમિત સપાટીનું ક્ષેત્રફળ
= 100 × 80 સેમી²

લંબાઈ અને પહોળાઈથી સીમિત સપાટીનું ક્ષેત્રફળ
= 200 × 100 સેમી²

લંબાઈ અને ઊંચાઈથી સીમિત 2 સપાટી માટે જરૂરી ટાઇલ્સ
= 2 × \(\frac{200 \times 80}{20 \times 20}\)
= 2 × \(\frac{200}{20} \times \frac{80}{20}\)
= 2 × 10 × 4 = 80

∴ પહોળાઈ અને ઊંચાઈથી સીમિત 2 સપાટી માટે જરૂરી ટાઇલ્સ
= 2 × \(\frac{100 \times 80}{20 \times 20}\)
= 2 × \(\frac{100}{20} \times \frac{80}{20}\)
= 2 × 5 × 4 = 40

∴ લંબાઈ અને પહોળાઈથી સીમિત 1 સપાટી માટે જરૂરી ટાઇલ્સ
= \(\frac{200 \times 100}{20 \times 20}=\frac{200}{20} \times \frac{100}{20}\) = 10 × 5 = 50

આમ, કુલ જરૂરી ટાઇલ્સની સંખ્યા = 80 + 40 + 50 = 170

→ લંબવૃત્તીય નળાકારનું પૃષ્ઠફળ: ઘણા બધા સમાન કદના વર્તુળાકાર કાગળના પૂંઠામાંથી કાપી અને તેની લંબરૂપે થપ્પી કરવાથી લંબવૃત્તીય નળાકાર (Right circular cylinder) મળે. જો કાગળનો આકાર વર્તુળ ન હોય અથવા તેમને લંબરૂપે ગોઠવવામાં ન આવે, તો લંબવૃત્તીય નળાકાર ન મળે. આપણે ફક્ત લંબવૃત્તીય નળાકારનો જ અભ્યાસ કરવાનો હોવાથી જો ઉલ્લેખ ના કરેલ હોય, તો નળાકાર શબ્દનો અર્થ લંબવૃત્તીય નળાકાર કરીશું.

→ નળાકારની સપાટીઓમાં તેની વક્ર સપાટી તથા તળિયા અને મથાળાની બે વર્તુળાકાર સમતલીય સપાટીનો સમાવેશ થાય. નળાકારના તળિયા અને પાયાની સમાન ત્રિજ્યાને નળાકારની ત્રિજ્યા પણ કહે છે. આમ, નળાકારની ત્રિજ્યા એટલે નળાકારના પાયાની ત્રિજ્યા તેમ સમજવું.

→ નળાકારની વક્ર સપાટીનું ક્ષેત્રફળ = 2πrh
અહીં, r = નળાકારની ત્રિજ્યા; h = નળાકારની ઊંચાઈ

→ નળાકારની વક્રસપાટીનું ક્ષેત્રફળ = πdh
જ્યાં, d = નળાકારનો વ્યાસ = 2r

→ નળાકારની વક્ર સપાટીનું ક્ષેત્રફળ = પાયાનો પરિઘ × ઊંચાઈ

→ નળાકારનું કુલ પૃષ્ઠફળ = 2π(r + h)

→ 11 એ અસંમેય સંખ્યા છે. πની દશાંશ અભિવ્યક્તિ અનંત અને અનાવૃત્ત હોય છે. પરંતુ, આપણે ગણતરીમાં તેની લગભગ કિંમત છે અથવા 3.14નો ઉપયોગ કરીશું.

નોંધઃ સમગ્ર પ્રકરણમાં અન્ય ઉલ્લેખ ન હોય, તો ની કિંમત \(\frac{22}{7}\) લેવી.

ઉદાહરણ : 1.
એક નળાકારની ત્રિજ્યા 28 સેમી અને ઊંચાઈ 90 સેમી છે, કે તો તેની વક્રસપાટીનું તેમજ કુલ સપાટીનું ક્ષેત્રફળ શોધો.
ઉત્તર:
આપેલ નળાકાર માટે ત્રિજ્યા r = 88 સેમી અને ઊંચાઈ h = 90 સેમી.
નળાકારની વક્રસપાટીનું ક્ષેત્રફળ = 2πrh
= 2 × 22 × 28 × 90 સેમી²
= 15,840 સેમી²

નળાકારની કુલ સપાટીનું ક્ષેત્રફળ = 2xr h + 1)
= 2 × 22 × 28(90 + 28) સેમી²
= 176 × 188 સેમી²
= 20,768 સેમી²

ઉદાહરણ : 2.
એક નળાકારની વક્ર સપાટીનું ક્ષેત્રફળ 1820 સેમી છે. જો તેની ઊંચાઈ 30 સેમી હોય, તો તેનો વ્યાસ શોધો.
ઉત્તર:
આપેલ નળાકાર માટે ઊંચાઈ h = 30 સેમી અને વક્રસપાટીનું ક્ષેત્રફળ = 1320 સેમી.
નળાકારની વક્રસપાટીનું ક્ષેત્રફળ = πdh
∴ 1320 = \(\frac{22}{7}\) × d × 30
∴ d = \(\frac{1320 \times 7}{22 \times 30}\) સેમી
∴ d = 14 સેમી
આમ, નળાકારનો વ્યાસ 14 સેમી છે.

ઉદાહરણ : 3.
ધાતુના એક પોલા નળાકારની લંબાઈ 70 સેમી છે. જો તેની અંદરના પોલા ભાગની ત્રિજ્યા 10 સેમી અને ધાતુની જાડાઈ 1 સેમી હોય, તો તેની બહારની તેમજ અંદરની વક્ર સપાટીઓના ક્ષેત્રફળનો તફાવત શોધો.
ઉત્તર:
ધાતુના પોલા નળાકાર માટે ઊંચાઈ h(લંબાઈ) = 70 સેમી, અંદરની ત્રિજ્યા r = 10 સેમી અને બહારની ત્રિજ્યા R= અંદરની ત્રિજ્યા +ધાતુની જાડાઈ = 10 + 1 સેમી = 11 સેમી. છે
પોલા નળાકારની બહારની તેમજ અંદરની વક્ર સપાટીઓના ક્ષેત્રફળનો તફાવત
= 2πRh – 2πrh
= 2πh(R – r)
= 2 × 22 × 70 (11 – 10)સેમી
= 440 સેમી

→ લંબવૃત્તીય શંકુ (Right circular cone) : કાટકોણ ત્રિકોણમાં ‘કાટખૂણો બનાવતી બાજુઓ પૈકીની એક બાજુને ધરી તરીકે લઈ તેની આસપાસ તે કાટકોણ ત્રિકોણને ઘુમાવતા અવકાશમાં જે ઘન આકૃતિ બને તેને લંબવૃત્તીય શંકુ કહે છે. જે શંકુમાં શિરોબિંદુને પાયાના કેન્દ્ર સાથે જોડતી રેખા પાયા સાથે કાટખૂણો બનાવતી ન હોય અથવા પાયો વર્તુળાકાર ન હોય તેને લંબવૃત્તીય શંકુ ન કહેવાય. આપણે માત્ર લંબવૃત્તીય શંકુનો જ અભ્યાસ કરવાના હોવાથી “શંકુનો અર્થ ‘લંબવૃત્તીય શંકુ’ ગણીશું.

→ શંકુને બે સપાટી હોય છે : એક વક્રસપાટી અને બીજી આધાર(પાયા)ની વર્તુળાકાર સપાટી. શંકુમાં ત્રણ માપ હોય છે :

• આધારની ત્રિજ્યા r
• ઊંચાઈ h અને
• તિર્થક (ત્રાંસી) ઊંચાઈ l. આ ત્રણેય માપ કાટકોણ ત્રિકોણની બાજુઓનાં માપ હોવાથી l² = r² + h² સંબંધ હંમેશાં જળવાય છે.

→ શંકુની વક્ર સપાટીનું ક્ષેત્રફળ = πrl

→ શંકુનું કુલ પૃષ્ઠફળ = πrl + πr² = πr(l + r)

→ કોઈ પણ શંકુ માટે, l² = r² + h²

ઉદાહરણ : 1.
એક શંકુની ત્રિજ્યા 15 સેમી અને તિર્યક ઊંચાઈ 25 સેમી છે, તો તેની વક્રસપાટીનું તથા કુલ સપાટીનું ક્ષેત્રફળ શોધો. (π = 3.14)
ઉત્તર:
આપેલ શંકુ માટે ત્રિજ્યા r = 15 સેમી અને તિર્યક ઊંચાઈ l = 25 સેમી.

શંકુની વક્રસપાટીનું ક્ષેત્રફળ = πrl
= 3.14 × 15 × 25 સેમી²
= 1177.5 સેમી²

શંકુની કુલ સપાટીનું ક્ષેત્રફળ = πr{l + 1)
= 3.14 × 15 (25 + 15) સેમી²
= 3.14 × 15 × 40 સેમી²
= 1884 સેમી²

ઉદાહરણ : 2.
એક શંકુની તિર્યક ઊંચાઈ 25 સેમી અને વક્રસપાટીનું ક્ષેત્રફળ 550 સેમી છે. શંકુની ત્રિજ્યા, કુલ સપાટીનું ક્ષેત્રફળ તથા ઊંચાઈ શોધો.
ઉત્તર:
આપેલ શંકુ માટે તિર્યક ઊંચાઈ = 25 સેમી અને વક્રસપાટીનું ક્ષેત્રફળ = 550 સેમી.

શંકુની વક્રસપાટીનું ક્ષેત્રફળ = πrl
∴ 550 = \(\frac{22}{7}\) × r × 25
∴ r = \(\frac{550 \times 7}{22 \times 25}\) સેમી
∴ r = 7 સેમી

શંકુની કુલ સપાટીનું ક્ષેત્રફળ = πr(l + r)
= \(\frac{22}{7}\) × 7 (25 + 7)સેમી²
= 22 × 32 સેમી²
= 704 સેમી²

હવે, શંકુ માટે, l² = r² + h²
25² = 7² + h²
h = 25² – 7² = 625 – 49 = 576 = (24)²
h = 24 સેમી

આમ, શંકુની ત્રિજ્યા 7 સેમી; કુલ સપાટીનું ક્ષેત્રફળ 704 સેમી² અને ઊંચાઈ 24 સેમી છે.

ઉદાહરણ : 3.
તાડપત્રીના એક શંકુ આકારના તંબુની ત્રિજ્યા 7 મી અને તિર્યક ઊંચાઈ 12 મી છે. આ તંબુ બનાવવા માટે 2 મી પહોળાઈની કેટલા મીટર તાડપત્રી જોઈએ? તાડપત્રીનો ભાવ પ્રતિમીટર 48 હોય, તો તાડપત્રીનો ખર્ચ શોધો.
ઉત્તર:
શંકુ આકારના તંબુ માટે ત્રિજ્યા r = 7 મી અને તિર્યક ઊંચાઈ 1 = 12 મી.

તંબુમાં વપરાતી તાડપત્રીનું ક્ષેત્રફળ = શંકુની વક્ર સપાટીનું ક્ષેત્રફળ
= πrl
= \(\frac{22}{7}\) × 7 × 12 મીટ
= 264 મીટ

તાડપત્રીનું ક્ષેત્રફળ = લંબાઈ × પહોળાઈ
264 = લંબાઈ × 2
લંબાઈ = 132 મી
આમ, તંબુ બનાવવા 132 મી લંબાઈની તાડપત્રી વપરાય.
1 મીટર તાડપત્રીનો ખર્ચ = ₹ 48
132 મીટર તાડપત્રીનો ખર્ચ = ₹ (132 × 48)
= ₹ 6336

→ ગોલક અથવા ગોળો (sphere) : પૂંઠામાંથી કાપેલ કોઈ વર્તુળને તેના કોઈ વ્યાસને ધરી તરીકે લઈ ઘુમાવવામાં આવે તો અવકાશમાં જે ઘન આકૃતિ બને તેને ગોલક અથવા ગોળો કહેવાય. ઘુમાવવામાં આવતા વર્તુળનું કેન્દ્ર એ જ ગોલકનું કેન્દ્ર છે અને તે વર્તુળની ત્રિજ્યા એ ગોલકની ત્રિજ્યા છે. ગોલકને એક જ વક્રસપાટી હોય છે.

→ અર્ધગોલક અથવા અર્ધગોળો (Hemisphere) : ગોલકને બરાબર વચ્ચેથી કાપીને બે સરખા ભાગમાં વહેંચતા બે અર્ધગોલક મળે. તેને બે જાતની સપાટી હોય છે. એક વક્ર સપાટી અને બીજી સપાટ વર્તુળાકાર સપાટી જેને અર્ધગોલકનો પાયો પણ કહે છે.

→ ગોલકની વક્રસપાટીનું ક્ષેત્રફળ = 4πr²
જ્યાં, r = ગોલકની ત્રિજ્યા

→ અર્ધગોલકની વક્ર સપાટીનું ક્ષેત્રફળ = 2πr²
જ્યાં, r = અર્ધગોલકની ત્રિજ્યા

→ અર્ધગોલકની કુલ સપાટીનું ક્ષેત્રફળ = 3πr²
જ્યાં, r = અર્ધગોલકની ત્રિજ્યા

ઉદાહરણ : 1.
14 સેમી ત્રિજ્યાવાળા ગોલકની સપાટીનું ક્ષેત્રફળ શોધો.
ઉત્તર:
આપેલ ગોલક માટે ત્રિજ્યા r = 14
સેમી ગોલકની સપાટીનું ક્ષેત્રફળ = 4πr²
= 4 × \(\frac{22}{7}\) × 14 × 14 સેમી²
= 2464 સેમી²

ઉદાહરણ : 2.
7 સેમી વ્યાસવાળા અર્ધગોલકની વક્રસપાટીનું તેમજ કુલ સપાટીનું ક્ષેત્રફળ શોધો.
ઉત્તર:
આપેલ અર્ધગોલક માટે ત્રિજ્યા
અર્ધગોલકની વક્રસપાટીનું ક્ષેત્રફળ
= 2πr²
= 2 × \(\frac{22}{7} \times \frac{7}{2} \times \frac{7}{2}\) સેમી²
= 77 સેમી²

અર્ધગોલકની કુલ સપાટીનું ક્ષેત્રફળ
= 3πr²
= 3 × \(\frac{22}{7} \times \frac{7}{2} \times \frac{7}{2}\) સેમી²
= 115.5 સેમી²

ઉદાહરણ : 3.
એક ગોલકની ત્રિજ્યા 3.5 સેમી છે. તેની સપાટીને સોનાનો ઢોળ ચડાવવાનો ખર્ચ પ્રતિ સેમી² ₹ 150 લેખે શોધો.
ઉત્તર:
આપેલ ગોલક માટે ત્રિજ્યા r = 3.5 સેમી = 3 સેમી = \(\frac{7}{2}\) સેમી
ગોલકની સપાટીનું ક્ષેત્રફળ = 4πr²
= 4 × \(\frac{22}{7} \times \frac{7}{2} \times \frac{7}{2}\) સેમી²
= 154 સેમી²

1 સેમી સપાટીને ઢોળ ચડાવવાનો ખર્ચ = ₹ 150
∴ 154 સેમી² સપાટીને ઢોળ ચડાવવાનો ખર્ચ
= ₹ (154 x 150)
= ₹ 23,100

ઉદાહરણ : 4.
એક ગોલક અને અર્ધગોલકની ત્રિજ્યાઓનો ગુણોત્તર ૩: 2 છે, તો ગોલકની સપાટીનું ક્ષેત્રફળ તથા અર્ધગોલકની કુલ સપાટીનું ક્ષેત્રફળનો ગુણોત્તર શોધો.
ઉત્તર:
ધારો કે, આપેલ ગોલકની ત્રિજ્યા = r₁ સેમી અને અર્ધગોલકની ત્રિજ્યા = r₂ સેમી
∴ r₁ : r₂ = 3: 2
∴ \(\frac{r_{1}}{r_{2}}=\frac{3}{2}\)
ગોલકની સપાટીનું ક્ષેત્રફળ 4gr અર્ધગોલકની કુલ સપાટીનું ક્ષેત્રફળ = 2

→ ઘનફળ (Volume) : ઘન પદાર્થ અવકાશમાં જગ્યા રોકે છે. આ રોકેલી જગ્યાના માપને તે ઘન પદાર્થનું ઘનફળ કહેવાય.

→ ક્ષમતા (Capacity): વાસણમાં સમાવી શકાતા વાયુ કે પ્રવાહીના ઘનફળને તે વાસણની ક્ષમતા (Capacity of the container) કહે છે.

→ લંબઘનનું ઘનફળ = પાયાનું ક્ષેત્રફળ × ઊંચાઈ
= લંબાઈ × પહોળાઈ × ઊંચાઈ
= l × b × h

→ સમઘનનું ઘનફળ = લંબાઈ × લંબાઈ × લંબાઈ
= a × a × a
= a³

→ સામાન્ય રીતે વાયુ અને પ્રવાહીના ઘનફળ લિટર, મિલિલિટર અથવા કિલોલિટરમાં દર્શાવવામાં આવે છે.

→ 1 મી³ = 1000 લિટર
1 લિટર = 1000 સેમી³ = 1000 મિલિલિટર
1 મી³ = 10,00,000 સેમી³ = 1 કિલોલિટર

ઉદાહરણ : 1.
ઈસ્ત્રીના દરેક ખોખાનાં માપ 30 સેમી × 15 સેમી × 10 સેમી છે. આવા 60 ખોખા સમાય તેવી પેટીનું ઘનફળ કેટલું થાય?
ઉત્તર:
આપેલ ઇસ્ત્રીના લંબઘન ખોખા માટે લંબાઈ l = 30 સેમી, પહોળાઈ b = 15 સેમી અને ઊંચાઈ h = 10 સેમી.
ઇસ્ત્રીના એક લંબઘન ખોખાનું ઘનફળ = lbh
= 30 × 15 × 10 સેમી³
= 4500 સેમી³ .

ઇસ્ત્રીના 60 ખોખા સમાય તેવી પેટીનું ઘનફળ
= 60 × 4500 સેમી³
= 2,70,000 સેમી³
= \(\frac{2,70,000}{10,00,000}\) મી (∵ 1 મી = 10,00,000 સેમી³)
= 0.27 મી³

ઉદાહરણ : 2.
એક સમઘન ખોખાની ધાર 8 સેમી છે, તો તેની કુલ સપાટીનું ક્ષેત્રફળ તેમજ ઘનફળ શોધો.
ઉત્તર:
આપેલ સમઘન ખોખા માટે ધાર a = 6 સેમી. સમઘનની કુલ સપાટીનું ક્ષેત્રફળ = 6a²
= 6 × 6 × 6 સેમી²
= 216 સેમી²

સમઘનનું ઘનફળ = a³
= 6 × 6 × 6 સેમી³
= 216 સેમી³

ઉદાહરણ : 3.
છત વગરના એક ઓરડાની લંબાઈ 12 મી, પહોળાઈ 4મી અને ઊંચાઈ ૩ મી છે. તે ઓરડામાં ગોઠવી શકાય તેવા લાંબામાં લાંબા સળિયાની લંબાઈ શોધો.
ઉત્તર:
આપેલ ઓરડા માટે લંબાઈ l = 12 મી, પહોળાઈ b = 4 મી અને ઊંચાઈ h = 3 મી.
ઓરડામાં ગોઠવી શકાય તેવા લાંબામાં લાંબા સળિયાની લંબાઈ
= \(\sqrt{l^{2}+b^{2}+h^{2}}\)
= \(\sqrt{12^{2}+4^{2}+3^{2}}\) મી
= \(\sqrt{169}\) મી
= 13 મી

ઉદાહરણ : 4.
એક લંબઘનના એક શિરોબિંદુ પર મળતી ત્રણ સપાટીઓનાં ક્ષેત્રફળ અનુક્રમે 700 સેમી², 300 સેમી અને 525 સેમી છે. તે લંબઘનનાં માપ તથા ઘનફળ શોધો.
ઉત્તર:
આપેલ લંબઘનની લંબાઈ, પહોળાઈ અને ઊંચાઈ અનુક્રમે l સેમી, bસેમી અને h સેમી છે.
એક શિરોબિંદુ પર મળતી ત્રણ લંબચોરસ સપાટીઓમાં એક સપાટી લંબાઈ અને પહોળાઈ દ્વારા,
બીજી સપાટી પહોળાઈ અને ઊંચાઈ દ્વારા અને ત્રીજી સપાટી ઊંચાઈ અને લંબાઈ દ્વારા બને.

∴ પહેલી સપાટીનું ક્ષેત્રફળ = lb = 700 સેમી²,
બીજી સપાટીનું ક્ષેત્રફળ = bh = 300 સેમી² અને
ત્રીજી સપાટીનું ક્ષેત્રફળ = hl = 525 સેમી²

∴ \(\frac{l b \times b h}{h l}=\frac{700 \times 300}{525}\)
∴ b² = 400
b = 20 સેમી
હવે, lb = 700 સેમી²
∴ l × 20 = 700
∴ l = 35 સેમી
અને bh = 300 સેમી²
∴ 20 × h = 300
∴ h = 15 સેમી

આમ, લંબઘનની લંબાઈ l = 35 સેમી, પહોળાઈ b = 20 સેમી અને ઊંચાઈ h = 15 સેમી.

લંબઘનનું ઘનફળ = lbh
= 35 × 20 × 15 સેમી³
= 10,500 સેમી³

નોંધઃ જો ઉપરોક્ત પ્રશ્નમાં ફક્ત ઘનફળ શોધવાનું કહ્યું હોય, તો લંબઘનનું ઘનફળ
= lbh
= \(\sqrt{l^{2} b^{2} h^{2}}\)
= \(\sqrt{l b \times b h \times h l}\) દ્વારા સરળતાથી મળે.

→ નળાકારનું ઘનફળ = પાયાનું ક્ષેત્રફળ ૪ ઊંચાઈ
= πr² × h
= πr²h જ્યાં, r = નળાકારની ત્રિજ્યા અને h = નળાકારની ઊંચાઈ છે.

ઉદાહરણ : 1.
એક નળાકારનું ઘનફળ 4620 સેમી અને ત્રિજ્યા 7 સેમી છે, તો તેની ઊંચાઈ શોધો.
ઉત્તર:
આપેલ નળાકાર માટે ત્રિજ્યા r =7 સેમી અને ઘનફળ = 4620 સેમી³
નળાકારનું ઘનફળ = πr²h
∴ 4620 = \(\frac{22}{7}\) × 7 × 7 × h
∴ \(\frac{4620 \times 7}{22 \times 7 \times 7}\) = h
∴ h = 30 સેમી

ઉદાહરણ : 2.
એક નળાકારની ત્રિજ્યા 14 સેમી અને વક્રસપાટીનું ક્ષેત્રફળ 4400 સેમી² છે, તો તેનું ઘનફળ શોધો.
ઉત્તર:
આપેલ નળાકાર માટે ત્રિજ્યા r = 14 સેમી અને
વકસપાટીનું ક્ષેત્રફળ = 4400 સેમી².
નળાકારની વક્રસપાટીનું ક્ષેત્રફળ = 2πrh
4400 = 2 × \(\frac{22}{7}\) × 14 × h
h = \(\frac{4400 \times 7}{2 \times 22 \times 14}\)
h = 50 સેમી

નળાકારનું ઘનફળ = πr²h
= \(\frac{22}{7}\) × 14 × 14 × 50 સેમી³
= 30,800 સેમી³

ઉદાહરણ : 3.
એક નળાકારની વક્ર સપાટીનું ક્ષેત્રફળ 3960 સેમી અને ઘનફળ 41,580 સેમી છે, તો તેની ત્રિજ્યા અને ઊંચાઈ શોધો.
ઉત્તર:
આપેલ નળાકાર માટે વક્રસપાટીનું ક્ષેત્રફળ = 3960 સેમી અને² ઘનફળ = 41,580 સેમી³

∴ r = 21 સેમી

નળાકારની વક્રસપાટીનું ક્ષેત્રફળ = 2πrh
∴ 3960 = 2 × \(\frac{22}{7}\) × 21 × h
∴h = \([latex]\)[/latex]
∴ h = 30 સેમી

ઉદાહરણ : 4.
1.4 સેમી ત્રિજ્યા અને 0.1 સેમી જાડાઈના 60 સિક્કા એકબીજા પર ગોઠવીને બનાવેલ સ્તંભનું ઘનફળ શોધો.
ઉત્તર:
આપેલ નળાકાર સિક્કા માટે ત્રિજ્યા r = 1.4 સેમી અને ઊંચાઈ (જાડાઈ) h = 0.1 સેમી.
એક નળાકાર સિક્કાનું ઘનફળ

= 36.96 સેમી

→ શંકુનું ઘનફળ = \(\frac{1}{3}\)πr²h; જ્યાં n = શંકુની ત્રિજ્યા અને h = શંકુની ઊંચાઈ છે.

ઉદાહરણ : 1.
એક શંકુની ત્રિજ્યા 10 સેમી અને તિર્યક ઊંચાઈ 26 સેમી છે, તો તેનું ઘનફળ શોધો. (π = 3.14)
ઉત્તર:
આપેલ શંકુ માટે ત્રિજ્યા r = 10 સેમી અને તિર્યક ઊંચાઈ
l = 26 સેમી.
l² = r² + h²
h² = l² – r²
= (26)² – (10)²
= 676 – 100 = 576 = (24)²
h = 24 સેમી

શંકુનું ઘનફળ = \(\frac{1}{3}\)πr²h
= \(\frac{1}{3}\) × 3.14 × 10 × 10 × 24 સેમી³
= 2512 સેમી³

ઉદાહરણ : 2.
એક શંકુની ત્રિજ્યા 7 સેમી અને વક્રસપાટીનું ક્ષેત્રફળ 550 સેમી છે. આ શંકુનું ઘનફળ શોધો.
ઉત્તર:
આપેલ શંકુ માટે ત્રિજ્યા r = 7 સેમી અને
વકસપાટીનું ક્ષેત્રફળ = 550 સેમી.
શંકુની વક્રસપાટીનું ક્ષેત્રફળ = πrl
550 = \(\frac{22}{7}\) × 7 × l
550 = 22 × l
l = \(\frac{550}{22}\)
l = 25 સેમી
l² = r² + h²
h² = l² – r²
= (25)² – (7)²
= 625-49 = 576 = (24)
h = 24 સેમી

શંકુનું ઘનફળ = \(\frac{1}{3}\)πr²h
= 2 × 7 × 7 × 24 સેમી³
= 1232 સેમી³

ઉદાહરણ : 3.
એક શંકુની ત્રિજ્યા અને તિર્યક ઊંચાઈનો ગુણોત્તર 3:5 છે અને તેની વક્રસપાટીનું ક્ષેત્રફળ 423.9 સેમી છે. આ શંકુનું ઘનફળ શોધો. (π = 3.14)
ઉત્તર:
આપેલ શંકુ માટે વકસપાટીનું ક્ષેત્રફળ = 423.9 સેમી² અને ત્રિજ્યા : તિર્યક ઊંચાઈ = 3: 5.

ધારો કે ત્રિજ્યા r = 3x સેમી, તો તિર્ધક ઊંચાઈ = 5x સેમી શંકુની વક્રસપાટીનું ક્ષેત્રફળ = πrl
423.9 = 3.14 × 3x × 5x
x² = \(\frac{423.9}{3.14 \times 3 \times 5}\)
x² = 9.

x = 3 આથી ત્રિજ્યા r = 3x = 3 × 3 = 9 સેમી અને તિર્યક ઊંચાઈ
l = 5x = 5 × 3 = 15 સેમી.
l² = r² + h²
h = l² – r²
= (15)² – (9)²
= 225 – 81 = 144 = (12)²
∴ h = 12 સેમી

શંકુનું ઘનફળ = \(\frac{1}{3}\)πr²h
= \(\frac{1}{3}\) × 3.14 × 9 × 9 = 12 સેમી³
= 1017.36 સેમી³

→ ગોળાનું ઘનફળ = \(\frac{4}{3}\)πr³ નક જ્યાં, r = ગોળાની ત્રિજ્યા છે.

→ અર્ધગોળાનું ઘનફળ = \(\frac{2}{3}\)πr³ જ્યાં, r = અર્ધગોળાની ત્રિજ્યા છે.

ઉદાહરણ : 1.
2.1 સેમી ત્રિજ્યાવાળા ગોળાનું ઘનફળ શોધો.
ઉત્તર:
આપેલ ગોળા માટે ત્રિજ્યા r = 2.1 સેમી = \(\frac{21}{10}\) સેમી.
ગોળાનું ઘનફળ = \(\frac{4}{3}\)πr³
= \(\frac{4}{3} \times \frac{22}{7} \times \frac{21}{10} \times \frac{21}{10} \times \frac{21}{10}\) સેમી³
= 38.808 સેમી³

ઉદાહરણ : 2.
12 સેમી વ્યાસવાળા અર્ધગોલકનું ઘનફળ શોધો. (π = 3.14)
ઉત્તર:
આપેલ અર્ધગોલક માટે ત્રિજ્યા
અર્ધગોલકનું ઘનફળ = \(\frac{2}{3}\)πr³
= \(\frac{2}{3}\) × 3.14 × 6 × 6 × 6 સેમી
= 452.16 સેમી³

ઉદાહરણ : 3.
6 સેમી ત્રિજ્યાવાળા ધાતુના એક ગોલકને પિગાળીને તેમાંથી 1 સેમી વ્યાસવાળો તાર બનાવવામાં આવે, તો તારની લંબાઈ કેટલી થાય?
ઉત્તર:
આપેલ ગોલકની ત્રિજ્યા r = 6 સેમી અને નળાકાર તાર માટે ત્રિજ્યા અને
લંબાઈ (ઊંચાઈ) = H સેમી. નળાકાર તારનું ઘનફળ = ગોલકનું ઘનફળ

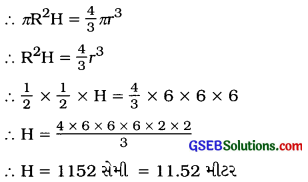
∴ H = 1152 સેમી = 11.52 મીટર
આમ, તારની લંબાઈ 11.52 મીટર થાય.

ઉદાહરણ : 4.
એક જમીનની બહાર આવેલ કોટ પર 21 સેમી વ્યાસવાળા લાકડાના ગોળાને નાના આધાર પર મૂકીને આકૃતિમાં દર્શાવ્યા મુજબ શણગારવામાં આવે છે. એ હેતુ માટે આવા 8 ગોળાનો ઉપયોગ કરવામાં આવે છે. ગોળાની નીચેનો નળાકાર આધાર 1.5 સેમી ત્રિજ્યા અને 7 સેમી ઊંચાઈવાળો છે. આ આધાર પર કાળો રંગ કરવાનો છે અને ગોળાને સિલ્વર રંગ કરવાનો છે. જો સિલ્વર રંગ કરવાનો ખર્ચ પ્રતિ સેમી 25 પૈસા અને 3 કાળો રંગ કરવાનો ખર્ચ 5 પૈસા પ્રતિ સેમી હોય, તો રંગ કરવાનો કુલ ખર્ચ શોધો.

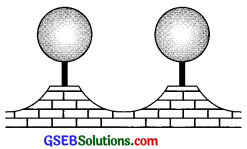
ઉત્તર:
લાકડાના ગોળાની ત્રિજ્યા
લાકડાના 1 ગોળાની વક્રસપાટીનું ક્ષેત્રફળ
= 4πr2
= 4 × \(\frac{22}{7} \times \frac{21}{2} \times \frac{21}{2}\) સેમી
= 1386 સેમી²

નળાકાર આધારના મથાળાની ત્રિજ્યા r = 1.5 સેમી
નળાકાર આધારના મથાળાનું ક્ષેત્રફળ
= πr²
= \(\frac{22}{7}\) × 1.5 × 1.5 સેમી²
= 7.07 સેમી² (આશરે)

આથી એક ગોળાને સિલ્વર રંગ કરવાની સપાટીનું ક્ષેત્રફળ = 1386 સેમી² – 7.07 સેમી² = 1378.93 સેમી²

∴ 8 ગોળાને સિલ્વર રંગ કરવાની સપાટીનું કુલ ક્ષેત્રફળ
= 1378.93 સેમી² × 8 = 11,031.44 સેમી²
25 પૈસા પ્રતિ સેમી² = ₹ 0.25 પ્રતિ સેમી²

1 સેમી વિસ્તારમાં સિલ્વર રંગ કરવાનો ખર્ચ = ₹ 0.25
∴ 11,031.44 સેમી. વિસ્તારમાં સિલ્વર રંગ કરવાનો ખર્ચ = ₹ (11,031.44 × 0.25)
= ₹ 2757.86 (આશરે).

નળાકાર આધાર માટે ત્રિજ્યા r = 1.5 સેમી અને ઊંચાઈ h = 7 સેમી

1 નળાકાર આધારની વક્રસપાટીનું ક્ષેત્રફળ
= 2πrh
= 2 × \(\frac{22}{7}\) × 1.5 × 7 સેમી = 66 સેમી

∴ 8 નળાકાર આધારની કાળો રંગ લગાવવાની વક્ર સપાટીનું કુલ ક્ષેત્રફળ = 66 સેમી² × 8 = 528 સેમી

5 પૈસા પ્રતિ સેમી = 0.05 પ્રતિ સેમી
1 સેમી. વિસ્તારમાં કાળો રંગ કરવાનો ખર્ચ = 0.05

528 સેમી. વિસ્તારમાં કાળો રંગ કરવાનો ખર્ચ
= ₹ (528 × 0.05) = ₹ 26.40

આમ, સિલ્વર રંગ તેમજ કાળો રંગ કરવાનો કુલ ખર્ચ
= ₹ 2757.86 + ₹ 26.40
= ₹ 2784.26 (આશરે)