This GSEB Class 9 Maths Notes Chapter 3 યામ ભૂમિતિ covers all the important topics and concepts as mentioned in the chapter.
યામ ભૂમિતિ Class 9 GSEB Notes
→ પ્રત્યેક વાસ્તવિક સંખ્યાને સંગત સંખ્યારેખા પર અનન્ય બિંદુ મળે અને આથી ઊલટું સંખ્યારેખા પરના પ્રત્યેક બિંદુને સંગત અનન્ય વાસ્તવિક સંખ્યા સંકળાય છે. અર્થાત્ સંખ્યારેખા અને વાસ્તવિક સંખ્યાઓના સમૂહ વચ્ચે એક-એક સંગતતા છે.
→ યામ-સમતલ પર આવેલ કોઈ પણ બિંદુ(કે વસ્તુ)નું સ્થાન વર્ણવવા માટે આપણને બે પરસ્પર લંબરેખાઓની જરૂર પડે છે.
→ યામ-સમતલમાં બિંદુનું સ્થાન દર્શાવવાની જે પદ્ધતિ ઉપયોગમાં લેવામાં આવે છે, તે મહાન ગણિતશાસ્ત્રી રેને દકાર્લેના નામ પરથી કાર્તેઝિય યામ પદ્ધતિ તરીકે ઓળખાય છે.
→ યામ-સમતલઃ સમતલમાં એક સમક્ષિતિજ (આડી) અને બીજી શિરોલંબ (ઊભી) એવી બે પરસ્પર લંબરેખાઓ દોરો. તેમના છેદબિંદુ અને ઉગમબિંદુ (Origin) કહેવામાં આવે છે. સમક્ષિતિજ (Horizontal) રેખાને x-અક્ષ અને શિરોલંબ (Vertical) રેખાને y-અક્ષ તરીકે ઓળખવામાં આવે છે.
→ બંને અક્ષોને યામાક્ષો (Coordinate axes) કહેવાય છે. સમતલને યામ-સમતલ (Coordinate plane) અથવા કાર્તેઝિય સમતલ (Cartesian plane) અથવા xy-સમતલ કહેવાય છે.
→ સંખ્યારેખા પરનાં બિંદુઓ અને વાસ્તવિક સંખ્યાઓના સમૂહ R વચ્ચે એક-એક સંગતતા છે. આથી x-અક્ષ તેમજ પુ-અક્ષ બંને પરના પ્રત્યેક બિંદુને સંગત અનન્ય વાસ્તવિક સંખ્યા મળે.
![]()
→ આપણે જાણીએ છીએ કે સંખ્યારેખા પર 0ની જમણી બાજુએ ધન સંખ્યાઓ અને તેની ડાબી બાજુએ ઋણ સંખ્યાઓનું નિરૂપણ થાય છે. તે જ રીતે, x-અક્ષ પર તેની જમણી બાજુએ ધન સંખ્યાઓ અને તેની ડાબી બાજુએ ઋણ સંખ્યાઓ આવેલ છે, એટલે કે ધન સંખ્યાઓ કિરણ OX પર અને ત્રણ સંખ્યાઓ કિરણ OX’ પર આવેલ છે. y-અક્ષ માટે તેની ઉપરની બાજુએ
ધન સંખ્યાઓ અને તેની નીચેની બાજુએ ત્રણ સંખ્યાઓ આવેલ છે, એટલે કે ધન સંખ્યાઓ કિરણ OY પર અને ત્રણ સંખ્યાઓ કિરણ OY’ પર આવેલ છે. કિરણો OX તથા OYને અનુક્રમે x-અક્ષ અને પુ-અક્ષની ધન દિશા કહેવાય છે. તે જ રીતે કિરણો OX’ અને OY’ને અનુક્રમે x-અક્ષ અને y-અક્ષની ઋણ દિશા કહેવાય છે.
→ વાસ્તવિક સંખ્યાઓની પ્રત્યેક ક્રમયુક્ત જોડ (a, b)ને સંગત બિંદુ L (a) અને M (b) અનુક્રમે x-અક્ષ તથા y-અક્ષ પર મળે. Lમાંથી x-અક્ષને લંબરેખા તથા Mમાંથી y-અક્ષને લંબરેખા Pમાં છેદે, તો Pને (a, b)ને સંગત સમતલનું બિંદુ કહે છે. તેને સંકેતમાં P (a, b) વડે દર્શાવાય છે. આથી ઊલટું સમતલના પ્રત્યેક બિંદુ P પરથી L (a) અને M (b) અક્ષો પર (Pથી અક્ષો ઉપર લંબ દોરીને) મેળવી શકાય. * વાસ્તવિક સંખ્યાઓની પ્રત્યેક ક્રમયુક્ત જોડ (a, b)ને સંગત અનન્ય બિંદુ P (a, b) સમતલમાં છે તથા સમતલના પ્રત્યેક બિંદુને સંગત અનન્ય ક્રમયુક્ત જોડ (a, b) એ વાસ્તવિક સંખ્યાઓની કમયુક્ત જોડ છે.
→ વને Pનો -યામ (x-coordinate) (કોટિ) તથા મને Pનો પ્રયામ (y-coordinate) (ભુજ) કહે છે.
→ કોઈ પણ બિંદુનો xયામ એ તેનું -અક્ષથી x-અક્ષની દિશામાં માપેલ લંબઅંતર છે. જો અંતર x-અક્ષની ધન દિશામાં માપવામાં આવે, તો તેનો xયામ ધન હોય છે અને જો અંતર x-અક્ષની ઋણ દિશામાં માપવામાં આવે, તો તેનો x-યામ ઋણ હોય છે. જ કોઈ પણ બિંદુનો પ્રયાસ તેનું x-અક્ષથી પુ-અક્ષની દિશામાં માપેલ લંબઅંતર છે. જો તે અંતર પુ-અક્ષની ધન દિશામાં માપવામાં આવે, તો તેનો પ્રયામ ધન હોય છે તથા જો તે અંતર -અક્ષની ઋણ દિશામાં માપવામાં આવે, તો તેનો પુનયામ ત્રણ હોય છે. બિંદુના યામ લખતી વખતે પ્રથમ xયામ અને તે પછી પુ-યામ લખવામાં આવે છે. યામને કૌંસમાં લખવામાં આવે છે.
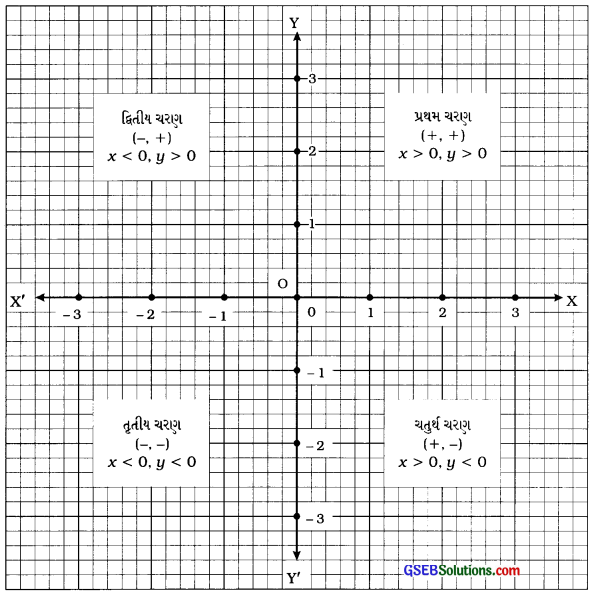
→ ચરણ (પાદ) (Quadrant) : કાર્તેઝિય યામ પદ્ધતિમાં લંબ યામાક્ષો (x-અક્ષ અને પુ-અક્ષ) સમતલને ચાર વિભાગોમાં વહેંચે છે.
| ચરણ | ભાગ | x-યામ | y-યામ |
| પ્રથમ ચરણ | ∠XOYનો અંદરનો ભાગ | + | + |
| દ્વિતીય ચરણ | ∠YOX’નો અંદરનો ભાગ | – | + |
| તૃતીય ચરણ | ∠X’OY’નો અંદરનો ભાગ | – | – |
| ચતુર્થ ચરણ | ∠Y’OXનો અંદરનો ભાગ | + | – |
→ સમતલમાં ઉગમબિંદુ Oના યામ (0, 0) છે.
→ X-અક્ષ પરના કોઈ પણ બિંદુને સંગત સંખ્યા એટલે કે xયામ વ હોય, પણ પુ-યામ ) હોય. (a, O) (જ્યાં, વ્ર વાસ્તવિક સંખ્યા છે.)
![]()
→ y-અક્ષ પરના કોઈ પણ બિંદુને સંગત સંખ્યા એટલે કે પુ-યામ b હોય, પણ 1-યામ 6 હોય. (0, b) (જ્યાં, કે વાસ્તવિક સંખ્યા છે.)
→ કોઈ પણ ચરણમાં આવેલ બિંદુના યામઃ કોઈ પણ ચરણમાં આવેલ બિંદુના યામ શોધવા તે બિંદુમાંથી x-અક્ષ પર અને y-અક્ષ પર લંબ દોરવામાં આવે છે. x-અક્ષ પર દોરેલ લંબના લંબપાદ દ્વારા આપેલ બિંદુનો દયામ મળે અને પુ-અક્ષ પર દોરેલ લંબના લંબપાદ દ્વારા આપેલ બિંદુનો પુ-યામ મળે.
ઉદાહરણ: 1.
નીચેની આકૃતિમાં દર્શાવેલ બિંદુઓના યામ જણાવોઃ
ઉત્તર:
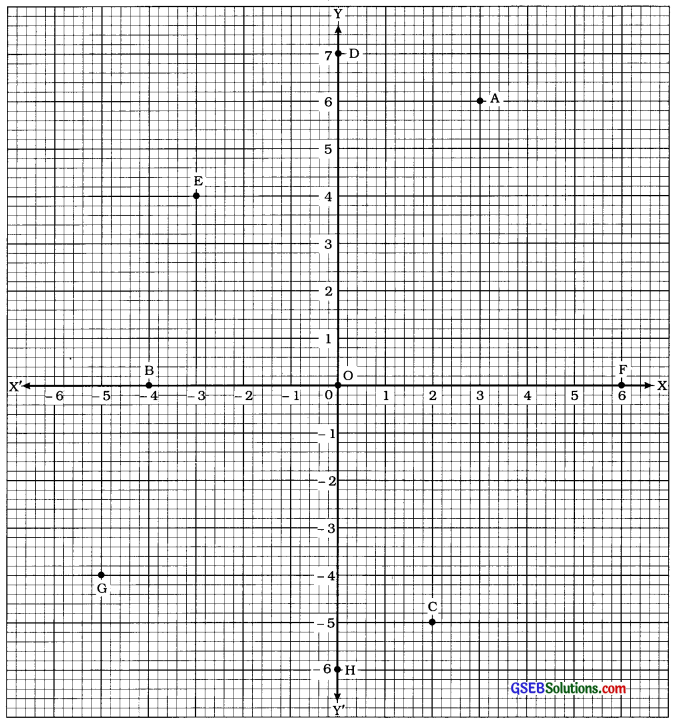
| બિંદુ | બિંદુના યામ |
| A | (3, 6) |
| B | (–4, 0) |
| C | (2, -5) |
| D | (0, 7) |
| E | (–3, 4) |
| F | (6, 0) |
| G | (- 5, – 4) |
| H | (0, – 6) |
| O | (0, 0) |
ઉદાહરણ: 2.
નીચેની આકૃતિમાં દર્શાવેલ બિંદુઓના યામ જણાવો. બંને અક્ષ પર પ્રમાણમાપ 1 સેમી = 5 એકમ છે:
ઉત્તર:
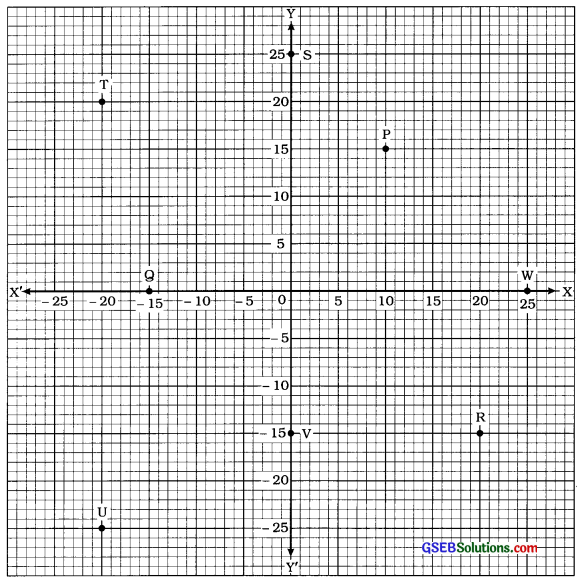
| બિંદુ | બિંદુના યામ |
| P | (10, 15) |
| Q | (-15, 0) |
| R | (20, -15) |
| S | (0, 25) |
| T | (-20, 20) |
| U | (-20, -25) |
| V | (0, – 15) |
| W | (25, 0) |
→ જે બિંદુના યામ આપેલા હોય તે બિંદુનું સમતલમાં નિરૂપણ (આલેખન) દા. ત., ક્રમયુક્ત જોડ (2, 3)ને સંગતબિંદુ સમતલમાં મેળવીએ. (2, 3)નો x-યામ અને y-યામ બંને ધન છે. x-અક્ષ પર તેની જમણી બાજુએ 2ને સંગતબિંદુ ખ મળશે. x-અક્ષની ઉપરના અર્ધતલમાં પુ-અક્ષ પર 3ને સંગતબિંદુ N મળશે. Mમાંથી ઇ-અક્ષને સમાંતર રેખા અને Nમાંથી x-અક્ષને સમાંતર રેખા દોરો. તેમનું અનન્ય છેદબિંદુ ? એ (2, 3)ને અનુરૂપ સમતલનું બિંદુ છે. P એ (2, 3)નો સમતલમાં આલેખ છે. (x, o) યામ ધરાવતું બિંદુ -અક્ષ પર હોય અને (o, y) યામ ધરાવતું બિંદુ પુ-અક્ષ પર હોય. નોંધઃ થોડા મહાવરા પછી અક્ષોને સમાંતર રેખાઓ દોરવાની
જરૂર નહીં પડે.
→ વાસ્તવિક સંખ્યાઓની બે ક્રમયુક્ત જોડ (x, y) અને (a, b) ત્યારે જ સમાન થાય જ્યારે x = a અને y = b હોય. એટલે કે x = a અને y = b હોય, તો અને તો જ (x, y) = (a, b).
![]()
ઉદાહરણઃ 1.
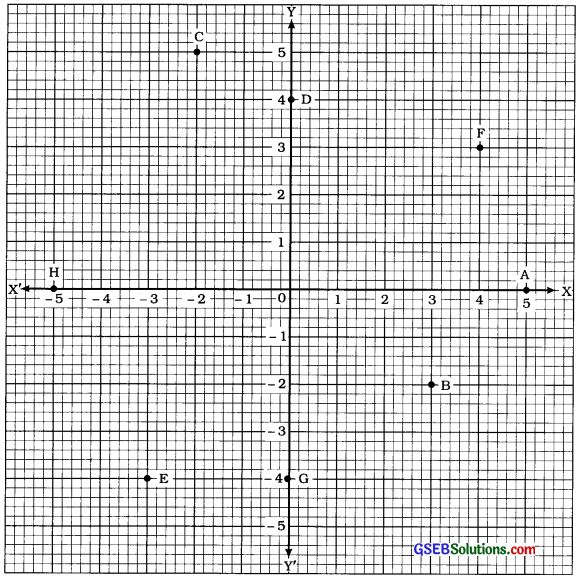
નીચેની યાદીમાં આપેલ બિંદુઓનું સ્થાન પામ-સમતલમાં ક્યાં હોય તે જણાવો. ત્યારબાદ તે બિંદુઓનું યામ-સમતલમાં નિરૂપણ કરો:
A(5, 0), B (3, -2), (-2, 5), D (0, 4), E -3, 4), (4, 3), G (0) -4), H (– 5, 0)
ઉત્તર:
| બિંદુ | બિંદનું સ્થાન |
| A (5, 0) | x-અક્ષ પર |
| B (3, -2) | ચતુર્થ ચરણમાં |
| C (-2, 5) | દ્વિતીય ચરણમાં |
| D (0, 4) | ઇ-અક્ષ પર |
| E (3, – 4) | તૃતીય ચરણમાં |
| F (4, 3) | પ્રથમ ચરણમાં |
| G (0 – 4) | y-અક્ષ પર |
| H (-5, 0) | x-અક્ષ પર |