This GSEB Class 9 Maths Notes Chapter 4 Lines and Angles covers all the important topics and concepts as mentioned in the chapter.
Lines and Angles Class 9 GSEB Notes
Linear equation in one variable:
ax + b = 0, a, b being real numbers, a ≠ 0 is the standard form of linear equation in one variable.
Linear equation in one variable ax + b = 0 has a unique solution or root \(\frac{-b}{a}\) which can be represented on the number line. In other words, the graph of a linear equation in one variable is a point on the number line.
Linear equation in one variable cam also be given in the forms like ax + b = cx + d;
where a, b, c, d are real numbers and a ≠ c or \(\frac{a x+b}{c x+d}\) = k; where a, b, c, d, k are real numbers, k ≠ 0, cx + d ≠ 0 and a ≠ kc.
Linear equation in two variables:
An equation having two variables both to power 1 and there is no product term xy is called a linear equation in two variables.
- The standard form of a linear equation in two variables is ax + by + c = 0, a, b, c are real numbers and a and b are not zero simultaneously, i.e., a2 + b2 ≠ 0.
- Whenever ax + by + c = 0 is referred as a linear equation in two variables, it implies that the conditions a, b, c are real numbers and a2 + b2 ≠ 0 are satisfied.
- Each linear equation in one variable can be expressed in the form of a linear equation in two variables.
Example 1:
Write each of the following equations In the form ax + by + c = 0 and indicate the values of a, b and e in each case:
(i) 2x + 3y = 4.37
Answer:
2x + 3y = 4.37 is written as 2x + 3y – 4.37 = O in the standard form.
Here. a = 2, b = 3 and c = -4.37.
(ii) x – 4 = √3y
Answer:
The equation x – 4 = y is written as x -√3y -4=0 in the standard form. Here,
a = 1, b = -√3 and c = -4.
(iii) 4 = 5x – 3y
Answer:
The equation 4 = 5x – 3y is written as 5x -3y -4 = O in the standard form. Here,
a = 5, b = -3 and c = -4.
It can also be written as – 5x + 3y + 4 = 0.
In the standard form. In this case a = -5, b = 3 and c = 4.
(iv) 2x = y
Answer:
The equation 2x = y Is written as 2x – y + 0 = 0 in the standard form. Here. a = 2, b = -1 and c = 0.
Example 2:
Write each of the following as an equation in two variables:
(i) x = – 5
Answer:
x = – 5 is written as 1x + 0y = – 5,
or
1x + 0y + 5 = 0.
(ii) y = 2
Answer:
y = 2 is written as 0x + 1y = 2, or
0x + 1y – 2 = 0.
(iii) 2x = 3
Answer:
2x = 3 is written as 2x + 0y – 3 = 0.
(iv) 5y = 2
Answer:
5y = 2 is written as 0x + 5y – 2 = 0.
![]()
Solutions of a linear equation in two variables:
For real numbers x and y, if (x, y) satisfies the equation ax + by + c = 0, then (x, y) is called a solution of ax + by + c = 0, a, b, c are real numbers and a2 + b2 ≠ 0.
If x = p and y = q is a solution of equation ax + by + c = 0, it is stated that ordered pair (p, q) is a solution of equation ax + by + c = 0.
A linear equation in two variables has infinitely many solutions.
e.g., (1, 9), (2, 8), (5. 5), (13, -3), (6.5, 3.5), \(\left(\frac{14}{3}, \frac{16}{3}\right)\), \(\left(\frac{\sqrt{5}}{2}, \frac{20-\sqrt{5}}{2}\right)\) are a11 solutions of the equation x + y = 10.
Easy way to find solutions of the equation ax + by + c = 0 is to convert the equation in its y-form as y = \(\frac{-c-a x}{b}\) and then to evaluate values of y for chosen values of x.
If only two solutions are to be found, it is easy to take x = 0 once and y = 0 the next.
Example 1:
Find four different solutions of the equation x + 2y = 6.
Answer:
Very simple calculation suggest that x = 2, y = 2 is a solution of the given equation, because for x = 2, y = 2
x + 2y = 2 + 4 = 6
Now, let us choose x = 0. With this value of x, the given equation reduces to 2y = 6 which has the unique solution y = 3. So, x = 0, y = 3 is also a solution of x + 2y = 6. Similarly, taking y = 0, the given equation reduces to x = 6. So, x = 6, y = 0 is a solution of x + 2y = 6 as well. Finally, let us take y = 1. The given equation now reduces to x + 2 = 6, whose solution is given by x = 4. Therefore, (4, 1) is also a solution of the given equation. So four of the infinitely many solutions of the given equation are: (2, 2), (0, 3), (6, 0) and (4, 1).
Example 2:
Find two solutions for each of the following equations:
(i) 4x + 3y = 12
Answer:
Taking x = 0, we get 3y = 12, i.e., y = 4. So, (0, 4) is a solution of the given equation. Similarly, by taking y = 0, we get x = 3. Thus, (3, 0) is also a solution.
(ii) 2x + 5y = 0
Answer:
Taking x = 0, we get 5y = 0, i.e., y = 0. So (0, 0) is a solution of the given equation. To get another solution, take x = 1, say. Then you can check that the corresponding value of y is – \(\frac{2}{5}\). So \(\left(1,-\frac{2}{5}\right)\) is another solution of 2x + 5y = 0.
(iii) 3y + 4 = 0
Answer:
Writing the equation 3y + 4 = 0 as 0x + 3y + 4 = 0, you will find that y = – \(\frac{4}{3}\) for any value of x. Thus, two solutions can be given as (0, –\(\frac{4}{3}\)) and (1, –\(\frac{4}{3}\)).
Graph of a linear equation in two variables:
We know that a solution (x, y) of the linear equation ax + by + c = 0 in two variables is a point in the coordinate plane. If all the solutions of ax + by + c = 0 are plotted in the coordinate plane, we get infinitely many points which are all collinear. The unique line passing through all these points is called the graph of the equation ax + by + c = 0.
Any point satisfying the equation lies on the graph of the equation and any point on the graph of the equation satisfies the equation.
As two points determine a line uniquely, it is sufficient to find just two points satisfying the equation and draw the line through those points. But, to be on the safer side we will always plot at least three solutions of the given equation to draw its graph.
Note:
ax + by + c = 0 is a polynomial equation of degree one in two variables x and y. The equation ax + by + c = 0 is called a linear equation, simply because its graphical representation is a straight line.
- The graph of x = 0 is the y-axis.
- The graph of y = 0 is the x-axis.
- The graph of x = k (constant k ≠ 0) is a line parallel to the y-axis, i.e., perpendicular to the x-axis.
- The graph of y = k (constant k ≠ 0) is a line parallel to the x-axis, i.e., perpendicular to the y-axis.
- The graph of ax + by = 0 (i.e., when c = 0) is a line passing through the origin.
- If a ≠ 0, b ≠ 0, c ≠ 0; the graph of ax + by + c = 0 is a line intersecting both the axes in distinct points ( \(\frac{-c}{a}\), 0) and (0, \(\frac{-c}{a}\))
Example 1:
Given the poInt (1, 2), find the equation of a line on which it lies. How many such equations are there?
Answer:
Here (1, 2) is a solution of a linear equation we are looking for. So, we are looking for any line passing through the point (1, 2). One example of such a linear equation is x + y – 3. Others are y – x – 1, y = 2x, since they are also satisfied by the coordinates of the point (1, 2). In fact, there are Infinitely many linear equations which are satisfied by the coordinates of the point (1, 2). From our knowledge of geometry. we know that Infinitely many lines pass through a given single point. Some more equations of the lines passing through (1, 2) are 3x + y = 5, 2x + 3y = 8, 5x – y = 3, etc.
Example 2:
Draw the graph of x + y = 7.
To draw the graph, we need at least two solutions of the equation. We can check that x = 0, y = 7 and x = 7, y = 0 are solutions , of the given equation. So, we can use the following table to draw the graph:
| X | 0 | 7 |
| y | 7 | 0 |
Draw the graph by plotting the two points from the table and then by joining the same by a line.
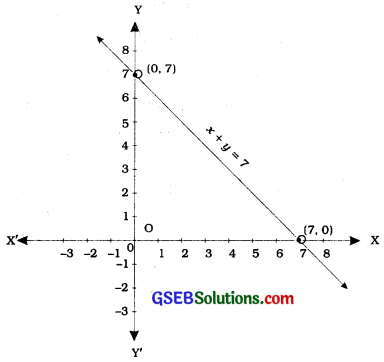
Note: Here, we can take one more point such as (3, 4) or (4, 3) or (5, 2)… as an additional point to avoid any calculating mistake.
Example 3:
You know that the force applied on a body is directly proportional to the acceleration produced in the body. Write an equation to express this situation and plot the graph of the equation.
Answer:
Here the variables involved are force and acceleration. Let the force applied be y units and the acceleration produced be x units. From ratio and proportion, we can express this fact as y = kx, where k is a constant. (From your study of science, you know that k is actually the mass of the body.)
Now, since we do not know what k is, we cannot draw the precise graph of y = kx.
However, if we give a certain value to k, then we can draw the graph. Let us take k = 3,
i. e., we draw the line representing y = 3x. For this we find two of its solutions, say (0, 0) and (2, 6).

From the graph, we can see that when the force applied is 3 units, the acceleration produced is 1 unit. Also, we note that (0, 0) lies on the graph which means the acceleration produced is 0 units, when the force applied is 0 units.
Remark: The graph of the equation of the form y = kx is a line which always passes through the origin.
Example 4:
For each of the graphs given in the following figures, select the equation whose graph it is from the choices given below:
(a) For figure
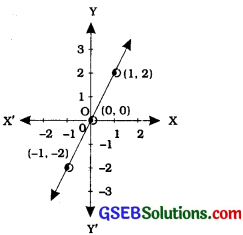
(i) x + y = 0
(ii) y = 2x
(iii) y = x
(iv) y = 2x + 1
Answer:
In figure , the points on the line are (-1, -2), (0, 0), (1, 2). By inspection, y = 2x is the equation corresponding to this graph. We can see that the y-coordinate in each case is double that of the x-coordinate.
(b)For figure
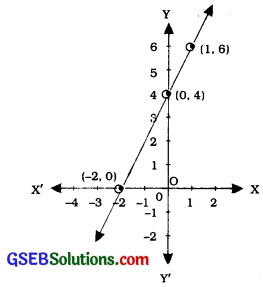
(i) x + y = 0
(ii) y = 2x
(iii) y = 2x + 4
(iv) y = x – 4
Answer:
In figure, the points on the line are (-2, 0), (0, 4), (1, 6). We see that the coordinates of the points of the graph (line) satisfy the equation y = 2x + 4. So, y = 2x + 4 is the equation corresponding to the graph in figure.
(c) For figure

(i) x + y = 0
(ii) y = 2x
(iii) y = 2x + 1
(iv) y = 2x – 4
Answer:
In figure (3), the points on the line are (-1, -6), (0, -4), (1, -2), (2, 0). By inspection, we can see that y = 2x – 4 is the equation corresponding to the given graph (line) as all those points satisfy the equation.
![]()
Example 5:
Solve the equation 2x + 1 = x – 3, and represent the solution (s) on
(i) the number line,
(ii) the Cartesian plane.
Answer:
We solve 2x + 1 = x – 3, to get
∴ 2x – x = – 3 – 1
x = – 4
(i) The representation of the solution on the number line is shown in the figure below, where x = – 4 is treated as an equation in one variable. x = -4

(ii) We know that x = – 4 can be written as x + 0y = – 4 which is a linear equation in two variables x and y. This is represented by a line. Now all the values of y are permissible because 0y is always 0. However, x must satisfy the equation x = – 4. Hence, two solutions of the given equation are x = – 4, y = 0 and x = – 4, y = 2.
Note that the graph AB is a line parallel to the y-axis (i.e., perpendicular to the x-axis) and at a distance of 4 units to the left of it (see the figure).
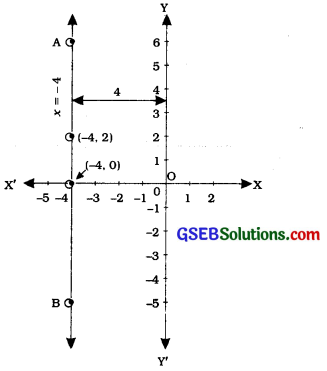
Similarly, the graph of equations like y = 3, i.e., 0x + 1y = 3 is a line parallel to the x-axis, i.e., perpendicular to the y-axis.
Graphs of special equations:
For the graph qf a linear equation ax + by + c = 0 in two variables:
- If a = 0 and c = 0, the equation reduces to y = 0 and its graph is the x-axis.
- If b = 0 and c = 0, the equation reduces to x = 0 and its graph is the y-axis.
- If a = 0 and c ≠ 0, the equation reduces to y = – \(\frac{c}{a}\) = p (a non-zero constant) and its graph is a line perpendicular to the y-axis and parallel to the x-axis.
- If b = 0 and c ≠ 0, the equation reduces to x = – \(\frac{c}{a}\) = q (a non-zero constant) and its a graph is a line perpendicular to the x-axis and parallel to the y-axis.
- If a ≠ 0, b ≠ 0 and c = 0, the equation reduces to ax + by = 0, i.e., y = mx, where m = – \(\frac{a}{b}\), and its graph is a line passing through the origin.
- If a ≠ 0, b ≠ 0 and c ≠ 0, the graph of the equation is a line intersecting both the axes at distinct points.