Gujarat Board GSEB Solutions Class 10 Maths Chapter 10 Circles Ex 10.2 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 10 Maths Chapter 10 Circles Ex 10.2
Question 1.
From a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. The radius of the circle is
(a) 7 cm
(b) 12cm
(c) 15 cm
(d) 24.5 cm
Solution:
(a) From the Fig.
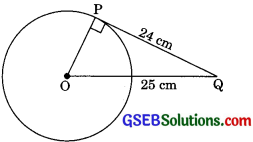
QP = 24cm
QO = 25cm .
Also, OP ⊥ PQ
[Radius through the point of contact is perpendicular to the tangent]
![]()
In right ΔOPQ, by Pythagoras theorem
OQ2 = OP2 + PQ2
252 = OP2 + 24
OP2 = 252 – 242
OP2 = 625 – 576 = 49
OP = 7 cm
Question 2.
In figure, if TP and TQ are the two tangents to a circle with centre O, so that ∠POQ = 110°, then ∠PTQ is equal to
(a) 60°
(b) 70°
(c) 80°
(d) 90°
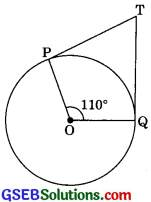
Solution:
(b) ∠OPT = ∠OQT = 90°
[Tangents perpendicular to the radius
through the point of contact]
In quadrilateral OPTQ
∠OPT + ∠PTQ + ∠OQT + ∠POQ = 360°
[Sum of all angles of quadrilateral]
⇒ 90° + ∠PTQ + 90° + 110° = 360°
290° + ∠PTQ = 360°
⇒ ∠PTQ = 360° – 290° = 70°
Question 3.
If tangents PA and PB from a point P to a circle with centre O are inclined to each other at an angle of 80°, then ∠POA is equal to:
(a) 50°
(b) 60°
(c) 70°
(d) 80°
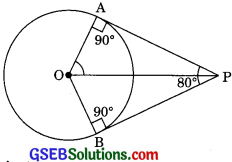
Solution:
(a) Join OP
In ΔPOA and ΔPOB
PA = PB [Tangents from external point P]
OA = OB
[Radii of same circle Common]
OP = OP
⇒ ΔPOA ≅ ΔPOB [SSS congruency rule]
⇒ ∠OPA = ∠OPB = 40°
Now, in ΔOAP
∠POA + ∠OAP + ∠APO = 180°
[Angle sum property of triangle]
∠POA + 90° + 40° = 180°
∠POA + 130° = 180°
∠POA = 50°
![]()
Question 4.
Prove that the tangent lines at the ends of a diameter of a circle are parallel.
Solution:
From Fig.
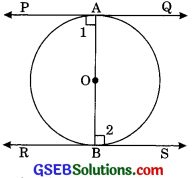
∠1 = 90° ……….(1)
[Radius is perpendicular to the tangent at the point of contact]
∠2 = 90° ……….(2)
From (1) and (2),
∠1= ∠2
But these are alternate interior angles.
∴ PQ || RS
Question 5.
Prove that the perpendicular at the point of contact to the tangent to a circle passes through the centre.
Solution:
Given:
A circle with centre O.
AB is a tangent at point A.
O’A ⊥ AB
To prove: AO’ passes through the centre O.
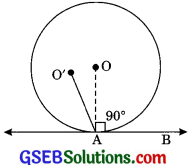
Construction: Join OA.
Proof: ∠O’AB = 90° (Given)
∠OAB = 90°
[Radius is perpendicular at the point of contact]
⇒ ∠O’AB = ∠OAB = 90°
which is possible only when O’ and O coincides
with each other.
⇒ AO’ and AO is the same line.
∴ AO’ passes through the centre O.
![]()
Question 6.
The length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.
Solution:
∠OPA = 90° [Theorem 10.1]
∴ OA2 = OP2 + AP2 [By Pythagoras theorem]
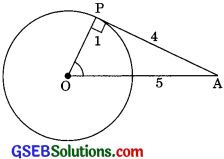
52 = OP2 + 42
OP2 = 25 – 16 = 9
OP = \(\sqrt{9}\) = 3 cm
∴ The radius of the circle is 3 cm.
Question 7.
Two concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.

Solution:
Let O be the common centre of two concentric circles.
AB, the chord of the larger circle which touches the smaller circle at M.
Join 0M and OA.
Then ∠OMA = 90° [Theorem 10.11]
∴ OMA is a right-angled triangle.
OA2 = OM2 + AM2 [By Pythagoras theorem]
52 + 32 + AM2
25 = 9 + AM2
AM2 = 25 – 9 = 16
AM = \(\sqrt{16}\) = 4cm
Now, AM = BM = 4 cm
[The perpendicular from the centre of a circle to a chord bisects the chord]
∴ AB = AM + BM
= AM + AM = 2AM
2 x 4 = 8 cm
![]()
Question 8.
A quadrilateral ABCD is drawn to circumscribe a circle (See Figure). Prove that AB + CD = AD +BC.
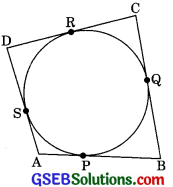
[CBSE 2008, 09, 12, 13, 16, 171
Solution:
Since the tangents drawn from an external point are equal in length.
∴ AP = AS ………(1)
BP = BQ ……..(2)
CR = CQ ………(3)
DR = DS ………(4)
Adding (1), (2), (3), (4), we get
(AP + BP) + (CR + DR)
⇒ AS + BQ + CQ + DS
⇒ AB + CD = (AS + DS) + (BQ + CQ)
⇒ AB + CD = AD + BC
Question 9.
In Fig. XY and X’Y’ are two parallel tangents to a circle with centre O and another tangent AB with the point of contact C intersecting XY at A and X’Y’ at B. Prove that ∠AOB = 90°. [CBSE 2011, 2012, 2013, 2017]
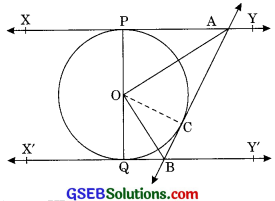
Solution:
Given: XY and X’Y’ are two parallel tangents with centre O and AB is another tangent at the point of contact C and intersecting XY at A and X’Y’ at B.
To prove: ∠AOB = 90°
Construction: Join OC.
Proof: ∠OPA = 90° [Theorem 10.11]
∠OCA = 90°
∴ In ΔOPA and ΔOCA
OA = OA (Common)
AP = AC [Tangents drawn from an external point are equal in length ]
and ∠OPA = ∠OCA = 90°
⇒ ΔSOPA ≅ ΔSOCA [RHS congruence criteria]
⇒ ∠OAP = ∠OAC [CPCT]
⇒ ∠OAC = \(\frac {1}{2}\) ∠PAB
Similarly, ∠OBQ = ∠OBC
⇒ ∠OBC = ∠QBA ……….(2)
∴ XY || XY,
and a transversal AB intersects them
⇒ ∠PAB + ∠QBA = 180° [Sum of the cointerior angles is 180° ]
⇒ \(\frac {1}{2}\) ∠PAB + \(\frac {1}{2}\)∠QBA = \(\frac {1}{2}\) x 180°
∠PAB + ∠QBA = 90° ………(3)
[From (1) and (2)]
In ΔAOB
∠OAC + ∠OBC + ∠AOB = 180°
[Angle sum property of triangle]
⇒ 90° + ∠AOB = 180° [From (3)]
∠AOB = 180° – 90° = 90°
∠AOB = 90°
![]()
Question 10.
Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segments joining the points of contact at the centre. [CBSE 2012]
Solution:
From Fig.
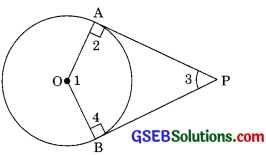
∠OPA = 90° ……..(1)
∠OBP = 90 ……….(2)
[Radius is perpendicular to the tangent at the point of contact]
Also, OAPB is a quadrilateral.
∴ ∠APB + ∠OBP + ∠AOB + ∠OAP = 360°
[Angle sum property of quadrilateral]
∠APB + 90° + ∠AOB + 90° = 360°
[From (1) and (2)]
∠APB + ∠AOB = 360° – 180° = 180°
∠APB and ∠AOB are supplementary angles.
Question 11.
Prove that the parallelogram circumscribing a circle is a rhombus. [CBSE 20121
Solution:
Given: ABCD is a parallelogram.
To prove: ABCD is a rhombus.
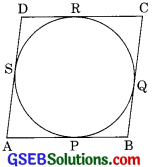
Proof: The tangents drawn from an external point are equal in length.
∴ AP = AS …….(1)
PB = BQ ………(2)
CR = CQ ……..(3)
DR = DS ……..(4)
Adding (1), (2), (3), (4), we get
AP + PB + CR + DR = AS + BQ + CQ + DS
⇒ (AP + PB) + (CR + DR) = (AS + DS) + (BQ + CQ)
⇒ AB + CD = AD + BC
⇒ AB + AB = BC + BC
(Opposite sides of parallelogram are equal]
⇒ 2AB = 2BC
⇒ AB = BC
Now AD = BC = AB = CD
⇒ ABCD is a rhombus.
![]()
Question 12.
A triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 8 cm and 6 cm respectively (See Figure). Find the sides AB and AC.
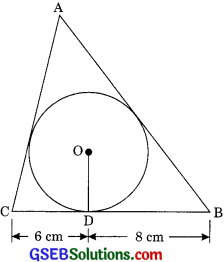
Solution:
Given CD 6 cm
BD = 8 cm and radius = 4 cm
Join OC, OA and OB.
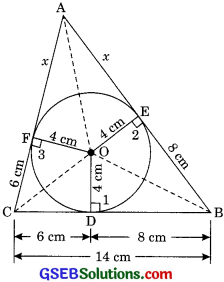
As the tangents drawn from an external point are equal in length
∴ CD = CF = 6cm
BD = BE = 8 cm
and let AF = AE = x cm
In ΔOCB,
Area of ΔOCB
= \(\frac {1}{2}\) base x height
= \(\frac {1}{2}\) x CB x OD
= \(\frac {1}{2}\) x 14 x 4 = 28 cm2
Similarly, Area of ΔOCA
= \(\frac {1}{2}\) x AC x OF
= \(\frac {1}{2}\) x (6 + x) x 4
= (12 + 2x) cm2
Similarly, Area of ΔOBA
= \(\frac {1}{2}\) x AB x OE
= (8 + x) x 4
=(16 + 2x) cm2
Now, area of ΔABC
= ar(OCB) + ar(OCA) + ar(OBA)
= 28 + (12 + 2x) + (16 + 2x)
= 56 + 4x …………(1)
Now, perimeter of ΔABC
= AB + BC + CA
= x + 6 + 14 + 8 + x
= 28 + 2x
S = \(\frac {1}{2}\) (28 + 2x) = 14 + x
By Heron’s formula,
area of ΔABC = \(\sqrt{S(S-a)(S-b)(S-c)}\)
= \(\sqrt{(14 + x)(14 + x – 14)(14 + x – x – 6)(14 + x – x – 8)}\)
= \(\sqrt{(14 + x) \cdot x \cdot(8)(6)}\)
= \(4 \sqrt{3 x(14 + x)}\) …….(2)
From equation (1) and (2), we get
56 + 4x = \(4 \sqrt{3 x (14 + x)}\)
14 + x = \(\sqrt{3 x(14 + x)}\)
On squaring both sides,
(14 + x)2 = 3x(14 + x)
14 + x = 3x
2x = 14
x = 7
∴ Length AC = 6 + x = 6 + 7 = 13cm
Length AB = 8 + x = 8 + 7 = 15 cm
![]()
Question 13.
Prove that the opposite sides of a quadrilateral circumscribing a circle subtended supplementary angles of the centre of the circle. [CBSE 2012, 2017]
Solution:
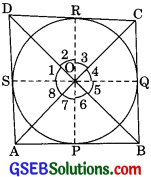
Given:
ABCD is a quadrilateral circumscribing a circle whose centre is O.
To prove:
(i) ∠BOC + ∠AOD = 180°
(ii) ∠AOB + ∠COD = 180°
Construction. Join OP, OQ, OR and OS;
where P, Q, R and S are points of contacts of tangents AB, BC, CD and DA to the circle.
Proof:
(i) As tangents drawn from an external point are equal in length.

In ΔOBP and ΔOBQ
OP = OQ [Radii of the same circle]
OB = OB [Common]
BP = BQ [From(1)]
∴ ΔOBP ≅ ΔOBQ [SSS congruency rule]
∴ ∠5 = ∠6 [CPCT]
Similarly,
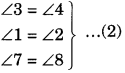
Now, ∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6 + ∠7 + ∠8 = 360°
[Sum angle property of quadrilateral]
= ∠1 + ∠1 + ∠4 + ∠4 + ∠5 + ∠5 + ∠8 + ∠8 = 360° [From (2)]
2[∠1 + ∠4 + ∠5+ ∠8] = 360°
∠1 + ∠4 + ∠5 + ∠8 = 180°
(∠1 + ∠8) + (∠4 + ∠5) = 180°
∠AOD + ∠BOC = 180°
(ii) Similarly, we can prove that
∠AOB + ∠COD = 180°
![]()