GSEB Solutions Class 10 Maths Chapter 11 Constructions Ex 11.1

Gujarat Board GSEB Solutions Class 10 Maths Chapter 11 Constructions Ex 11.1 Textbook Questions and Answers.

Gujarat Board Textbook Solutions Class 10 Maths Chapter 11 Constructions Ex 11.1

Question 1.
Draw a line segment of length 7.6 cm and divide it in the ratio 5 : 8. Measure the two parts.
Solution:
Steps of Construction
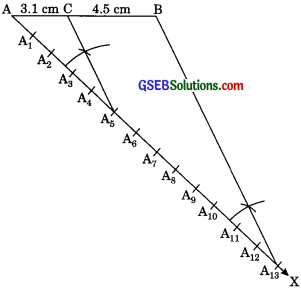
1. Draw AB = 7.6 cm
2. At A, draw an acute angle ∠BAX below BA.
3. On AX mark 13 (5 + 8) arcs A₁, A₂, …, A₁₃.
4. Join B to A₁₃.
5. From A₅, draw A₅C || A₁₃B.
AC : CO = 5 : 8.

Justification:
In ΔABA₁₃, A₅C || A₁₃
⇒ \(\frac {AC}{BC}\) = \(\frac{\mathrm{AA}_{5}}{\mathrm{A}_{5} \mathrm{A}_{13}}\) [Thales Theorem]
But \(\frac{\mathrm{AA}_{5}}{\mathrm{A}_{5} \mathrm{A}_{13}}\) = \(\frac {5}{8}\)
[By construction]
∴ \(\frac {AC}{BC}\) = \(\frac {5}{8}\)

Question 2.
Construct a triangle of sides 4 cm, 5 cm and 6 cm and then a triangle similar to it whose sides are of the corresponding sides of the first triangle.
Solution:
Steps of Construction:
1. Draw ΔABC with AC = 6cm, AB = 5 cm, BC = 4 cm.
2. At A₁ draw an acute angle∠CAX below the base AC.
3. Mark 3 arcs on AX such that AA₁ = A₁A₂ = A₂A₃.
4. Join A₃C.
5. Draw A₂C’ || A₃C
6. From C’ draw B’C’ || BC

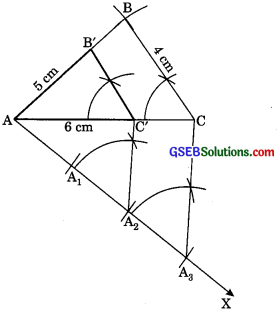
Thus, ΔAB’C’ is the required triangle.

Justification:
ΔAB’C’ ∼ ΔABC [AA similarity Rule]
\(\frac{\mathrm{AB}^{\prime}}{\mathrm{AB}}=\frac{\mathrm{AC}^{\prime}}{\mathrm{AC}}=\frac{\mathrm{B}^{\prime} \mathrm{C}^{\prime}}{\mathrm{BC}}\) ……….(1)
[Sides are proportional]
But \(\frac{A C^{\prime}}{A C}=\frac{A A_{2}}{A A_{3}}=\frac{2}{3}\) ………..(2)
From (1) and (2)
But \(\frac{A B^{\prime}}{A B}=\frac{A C^{\prime}}{A C}=\frac{B^{\prime} C^{\prime}}{B C}=\frac{2}{3}\)

Question 3.
Construct a triangle with sides 5 cm, 6 cm and 7 cm and then another triangle whose sides are \(\frac {5}{8}\) of the corresponding sides of the first triangle.
Solution:
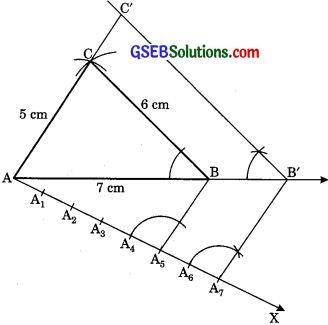
1. Construct a ΔABC with AB = 7 cm, AC = 5 cm, BC = 6 cm
2. At A draw an acute ∠BAX below AB.
3. On AX, mark 7 arcs A₁, A₂, …, A₇ such that
AA₁ = A₁A₂ =…=A₆A₇.
4. Join A₅B.
5. From A₇ draw A₇B’ || A₅B meeting AB at B’ (extent AB to B’)
6. From B’ draw B’C’ || BC meeting AC at C’ [extend AC to C’]
AB’C’ is the required triangle each of whose sides is \(\frac {5}{8}\) of the corresponding sides of ΔABC.

Justification:
\(\frac{C^{\prime} A}{C A}=\frac{A B^{\prime}}{A B}=\frac{C^{\prime} B^{\prime}}{C B}\) ………..(1)
[Sides are proportional]
But \(\frac{\mathrm{AB}^{\prime}}{\mathrm{AB}}=\frac{\mathrm{AA}_{7}}{\mathrm{AA}_{5}}\) = \(\frac {7}{5}\) ………(2)
From (1) and (2)
\(\frac{C^{\prime} A}{C A}=\frac{A B^{\prime}}{A B}=\frac{C^{\prime} B^{\prime}}{C B}\) = \(\frac {7}{5}\)

Question 4.
Construct an isosceles triangle whose base is 8 cm and altitude is 4 cm and then another triangle whose sides are 1 times the corresponding sides of the isosceles triangle. (CBSE 2017)
Solution:
Steps of Construction:
1. Draw a line segment BC = 8 cm.
2. Draw its perpendicular bisector AD (4 cm).
3. Joining AB and AC, we get isosceles triangle ABC

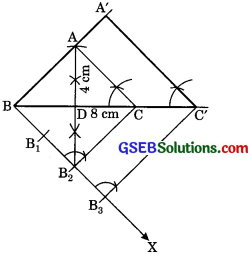
4. Construct an acute ∠CBX.
5. Along BX cut 3 arcs B₁, B₂ and B₃ such that
BB₁ = B₁B₂ = B₂B₃.
6. Join C to B₂ and draw a line B₃C’ || B₂C [extend BC to C’]
7. From C’ draw C’A’ || CA [extend BA to A’]
∴ ΔA’BC’ is a required triangle.

Justification:
Now C’A’ || CA (By construction)
∴ ΔABC ∼ ΔA’BC’ [AA similarity criteria]
∴ \(\frac{\mathrm{A}^{\prime} \mathrm{B}}{\mathrm{AB}}=\frac{\mathrm{A}^{\prime} \mathrm{C}^{\prime}}{\mathrm{AC}}=\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}\) [Sides are proportional]
Now B₃C’ || B₂C (By construction)
∴ ΔBB₃C’ – ΔBB₂C [AA similarity criteria]
∴ \(\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{BB}_{3}}{\mathrm{BB}_{2}}\) [Thales theorem]
But \(\frac{\mathrm{BB}_{3}}{\mathrm{BB}_{2}}=\frac{3}{2}\) (By construction]
∴ \(\frac{B C^{\prime}}{B C}=\frac{3}{2}\)
∴ \(\frac{\mathrm{A}^{\prime} \mathrm{B}}{\mathrm{AB}}=\frac{\mathrm{A}^{\prime} \mathrm{C}^{\prime}}{\mathrm{AC}}=\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{3}{2}\)

Question 5.
Draw a triangle ABC with side BC = 6 cm, AB = 5 cm and ∠ABC = 60°. Then construct a triangle whose sides are \(\frac{3}{4}\) of the corresponding sides of the ABC. (CBSE 2015)
Solution:
Steps of Construction:
1. Draw a line segment BC = 6 cm.
2. At B draw ∠CBY = 60° on which take AB = 5 cm.
3. Join AC. ΔABC is required triangle.

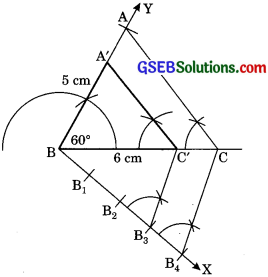
4. From B, draw an acute ∠CBX downwards.
5. Mark four arcs B₁, B₂, B₃, B₄ on BX such that BB₁ = B₁B₂ = B₂B₃ = B₃B₄.
6. Join B₄C and from B₃ draw B₃C’ B₄C.
7. From C’, draw A’C’ || AC.
When ΔA’BC’ is the required triangle whose sides are \(\frac{3}{4}\) of the corresponding sides of ΔABC.

Justification:
A’C’ || AC (By construction)
∴ ΔA’BC’ ∼ ΔABC (AA similarity Rule)
∴ \(\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{BB}_{3}}{\mathrm{BB}_{2}}\) ………..(1)
[Sides are proportional]
But \(\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{BB}_{3}}{\mathrm{BB}_{4}}=\frac{3}{4}\) ………….(2)
From (1) and (2)
\(\frac{\mathrm{A}^{\prime} \mathrm{B}}{\mathrm{AB}}=\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{A}^{\prime} \mathrm{C}^{\prime}}{\mathrm{AC}}=\frac{3}{4}\)

Question 6.
Draw a triangle ABC with side BC = 7 cm, ∠B = 45°, ∠A = 105°. Then construct a triangle whose sides are \(\frac{3}{4}\) times the corresponding sides of the ΔABC. (CBSE 2012, 2017)
Solution:
Steps of Construction:
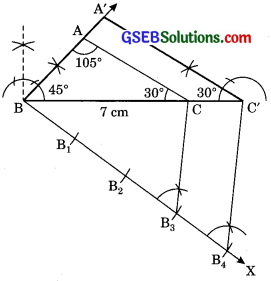
1. Draw a ABC with side BC = 7 cm, ∠B = 45°, ∠C = 30°
[∠C = 180° – 45° – 105° = 180° – 150° = 30°]
2. At B, draw an acute ∠CBX below BC.
3. On BX, mark the arcs B₁, B₂, B₃, B₄ such
that BB₁ = B₁B₂ = B₂B₃ = B₁B₄.
4. Join B₃C.
5. Draw B₄C’|| B₃C [Extend BC to C’]
6. Draw C’A’ || CA [Extend BA to A’]
∴ ΔA’BC’ is the required triangle.

Justification:
C’A’ || CA (By construction)
∴ ΔABC ∼ ΔA’BC’ (AA similarity Criteria)
\(\frac{\mathrm{A}^{\prime} \mathrm{B}}{\mathrm{AB}}=\frac{\mathrm{A}^{\prime} \mathrm{C}^{\prime}}{\mathrm{AC}}=\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}\) ………(1) [Corresponding sides are proportional]
Now B₄C’ || B₃C (By construction)
∴ \(\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{BB}_{4}}{\mathrm{BB}_{3}}\) ……..(2)
[Thales theorem]
But = \(\frac{B B_{4}}{B B_{3}}=\frac{4}{3}\) ………(3) (By construction)
From (1) (2) and (3)
\(\frac{\mathrm{A}^{\prime} \mathrm{B}}{\mathrm{AB}}=\frac{\mathrm{A}^{\prime} \mathrm{C}^{\prime}}{\mathrm{AC}}=\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{4}{3}\)

Question 7.
Draw a right triangle in which the sides (other than hypotenuse) are of lengths 4 cm and 3 cm. Then construct another triangle whose sides are times the corresponding sides of the given triangle. (CBSE 2010)
Solution:
1. Draw a line segment AB = 4 cm.
2. By making right angle at B. Draw BC = 3 cm.

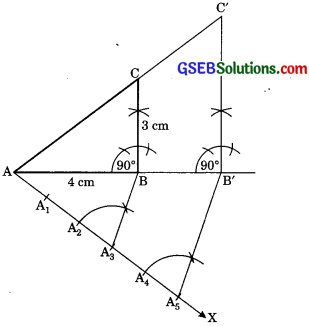
3. Join AC. ΔABC is the required right-angled triangle.
4. At A, Draw acute angle ∠BAX downwards.
5. On AX, mark 5 arcs A₁, A₂, A₃, A₄, A₅ such
that AA₁ = A₁A₂ = … = A₄A₅
6. Join A₃B.
7. Draw A₅B’|| A₃B [Extend AB to B’]
8. Draw B₁C’ || BC [Extend AC to C’]
Hence ΔAB’C’ is the required triangle

Justification:
ΔABC ∼ ΔABC(AA similarity Rule)
\(\frac{A B^{\prime}}{A B}=\frac{A C^{\prime}}{A C}=\frac{B^{\prime} C^{\prime}}{B C}\) ……..(1) [Sides are proportional]
But \(\frac{A B^{\prime}}{A B}=\frac{A A_{5}}{A A_{3}}=\frac{5}{3}\) ……(2)
From (1) and (2)
\(\frac{A B^{\prime}}{A B}=\frac{A C^{\prime}}{A C}=\frac{B^{\prime} C^{\prime}}{B C}=\frac{5}{3}\)