Gujarat Board GSEB Solutions Class 10 Maths Chapter 12 વર્તુળ સંબંધિત ક્ષેત્રફળ Ex 12.2 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 10 Maths Chapter 12 વર્તુળ સંબંધિત ક્ષેત્રફળ Ex 12.2
નોંધઃ ઉલ્લેખ કર્યો ન હોય, તો π = \(\frac{22}{7}\) લો.
પ્રશ્ન 1.
જો 6 સેમી ત્રિજ્યાવાળા વર્તુળના વૃત્તાંશ દ્વારા કેન્દ્ર આગળ બનતો ખૂણો 60° હોય, તો વૃત્તાંશનું ક્ષેત્રફળ શોધો.
ઉત્તર:
વર્તુળના આપેલ વૃત્તાંશ માટે, ત્રિજ્યા r = 6 સેમી અને
વૃતાંશનો ખૂણો θ = 60°.
લધુવૃત્તાંશનું ક્ષેત્રફળ = \(\frac{\theta}{360}\) × πr2
= \(\frac{60}{360} \times \frac{22}{7}\) × 6 × 6 સેમી2
= \(\frac{132}{7}\) સેમી2
આમ, આપેલ વૃત્તાંશનું ક્ષેત્રફળ \(\frac{132}{7}\) સેમી2 છે.

પ્રશ્ન 2.
22 સેમી પરિઘવાળા વર્તુળના ચતુર્થાશનું ક્ષેત્રફળ શોધો.
ઉત્તર:
ધારો કે, આAPB એ એક વર્તુળનો ચતુર્થાશ છે અને તે વર્તુળનો પરિઘ 22 સેમી છે.
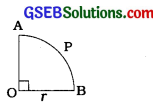
2πr = 22
2 × \(\frac{22}{7}\) × r = 22
r = \(\frac{7}{2}\) સેમી
આમ, વર્તુળના ચતુર્થાશની ત્રિજ્યા r = \(\frac{7}{2}\) સેમી
વર્તુળના ચતુર્થાશનું ક્ષેત્રફળ = \(\frac{1}{4}\) πr2
= \(\frac{1}{4} \times \frac{22}{7} \times \frac{7}{2} \times \frac{7}{2}\) સેમી2
= \(\frac{77}{8}\) સેમી2
આમ, વર્તુળના આપેલ ચતુર્થાશનું ક્ષેત્રફળ \(\frac{77}{8}\) સેમી2 છે.

પ્રશ્ન 3.
એક ઘડિયાળના મિનિટ-કાંટાની લંબાઈ 14 સેમી છે. મિનિટ કાંટો 5 મિનિટમાં પરિભ્રમણ કરીને જે ક્ષેત્રફળ આવરે તે શોધો. ઘડિયાળનો મિનિટ-કાંટો 60 મિનિટ, એટલે કે, 1 કલાકમાં એક પૂર્ણ પરિભ્રમણ કરે છે.
ઉત્તર:
∴ 60 મિનિટમાં મિનિટ-કાંટાએ કેન્દ્ર આગળ આંતરેલો ખૂણો = 360°.
∴ 5 મિનિટમાં મિનિટ-કાંટાએ કેન્દ્ર આગળ આંતરેલો ખૂણો = \(\frac{5}{60}\) × 360° = 30°.
આથી 5 મિનિટમાં મિનિટ-કાંટો જે વિસ્તાર આવરી લે તે લઘુવૃત્તાશ થાય. જેની ત્રિજ્યા r = મિનિટ-કાંટાની લંબાઈ = 14
સેમી અને વૃત્તાંશનો ખૂણો θ = 30°.
લધુવૃત્તાંશનું ક્ષેત્રફળ = \(\frac{\theta}{360}\) × π r2
= \(\frac{30}{360} \times \frac{22}{7}\) × 14 × 14 સેમી2
= \(\frac{154}{3}\) સેમી2
આમ, મિનિટ-કાંટો 5 મિનિટમાં \(\frac{154}{3}\) સેમી2 ક્ષેત્રફળ આવરે છે.

પ્રશ્ન 4.
10 સેમી ત્રિજ્યાવાળા વર્તુળની જીવા કેન્દ્ર આગળ કાટખૂણો આંતરે છે. તેને અનુરૂપ
(i) લઘુવૃત્તખંડ
(ii) ગુરુવૃત્તાંશનું ક્ષેત્રફળ શોધો. (π = 3.14 લો.)
ઉત્તર:
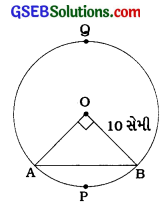
અહીં, વર્તુળની ત્રિજ્યા r = 10 સેમી અને લઘુવૃત્તાંશનો ખૂણો θ = 90°.
લઘુવૃત્તાંશનું ક્ષેત્રફળ = \(\frac{\theta}{360}\) × π r2
= \(\frac{90}{360}\) × 3.14 × 10 × 10 સેમી2
= 78.5 સેમી2
∆ AOBમાં, ∠O = 90°
∆ AOBનું ક્ષેત્રફળ = \(\frac{1}{2}\) × OA × OB
= \(\frac{1}{2}\) × 10 × 10 સેમી
= 50 સેમી2
લઘુવૃત્તખંડનું ક્ષેત્રફળ = લઘુવૃત્તાંશનું ક્ષેત્રફળ – ∆ AOBનું ક્ષેત્રફળ
= (78.5 – 50) સેમી2 = 28.5 સેમી2
ગુરુવૃત્તાંશનું ક્ષેત્રફળ = વર્તુળનું ક્ષેત્રફળ – લઘુવૃત્તાંશનું ક્ષેત્રફળ = (π r2 – 78.5) સેમી2
= (3.14 × 10 × 10 – 78.55 સેમી2
= (314 – 78.5) સેમી2 = 235.5 સેમી2
આમ, લઘુવૃત્તખંડનું ક્ષેત્રફળ 28.5 સેમી2 અને ગુરુવૃત્તાંશનું ક્ષેત્રફળ 235.5 સેમી2 થાય.

પ્રશ્ન 5.
21 સેમી ત્રિજ્યાવાળા વર્તુળનું એક ચાપ કેન્દ્ર આગળ 60°નો ખૂણો આંતરે છે. તેને અનુરૂપ
(i) ચાપની લંબાઈ
(ii) ચાપ વડે બનતા વૃત્તાંશનું ક્ષેત્રફળ
(iii) અનુરૂપ જીવા વડે બનતા વૃત્તખંડનું ક્ષેત્રફળ શોધો.
ઉત્તર:
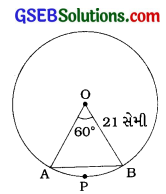
આપેલ વર્તુળ માટે ત્રિજ્યા r = 21 સેમી અને લઘુવૃત્તાશનો ખૂણો θ = ચાપ APB એ કેન્દ્ર આગળ આંતરેલો ખૂણો = 60°.
ચાપ APBની લંબાઈ = \(\frac{\theta}{360}\) × 2πr A rs
= \(\frac{60}{360}\) × 2 × \(\frac{22}{7}\) × 21 સેમી
= 22 સેમી
લઘુવૃત્તાંશ OAPBનું ક્ષેત્રફળ = \(\frac{\theta}{360}\) × πr2
= \(\frac{60}{360} \times \frac{22}{7}\) × 21 × 21 સેમી2
= 231 સેમી2
∆ OABમાં, ∠O = 60° અને OA = OB = 21 સેમી .
∆ OABમાં, ∠A + ∠B = 120° અને ∠A = ∠B.
∆ OABમાં, ∠A = ∠B = ∠O = 60°
∆ OAB એ સમબાજુ ત્રિકોણ છે. જેમાં દરેક બાજુની લંબાઈ a = 21 સેમી.
સમબાજુ ∆ OABનું ક્ષેત્રફળ = \(\frac{\sqrt{3}}{4}\) a2
= \(\frac{\sqrt{3}}{4}\) × 21 × 21 સેમી2
= \(\frac{441 \sqrt{3}}{4}\) સેમી2
લઘુવૃત્તખંડ APBનું ક્ષેત્રફળ = લઘુવૃત્તાંશ OAPBનું ક્ષેત્રફળ – ∆ CABનું ક્ષેત્રફળ
= (231 – \(\frac{441 \sqrt{3}}{4}\)) સેમી2
આમ, ચાપની લંબાઈ 22 સેમી, ચાપ વડે બનતા લઘુવૃત્તાંશનું ક્ષેત્રફળ 231 સેમી અને લઘુત્તખંડનું ક્ષેત્રફળ (231 – \(\frac{441 \sqrt{3}}{4}\)) સેમી2 થાય.

પ્રશ્ન 6.
15 સેમી ત્રિજ્યાવાળા વર્તુળની જીવા કેન્દ્ર આગળ 60નો ખૂણો આંતરે છે. તેને અનુરૂપ લઘુવૃત્તખંડ અને ગુરુવૃત્તખંડનું ક્ષેત્રફળ શોધો. (π = 3.14 અને √3= 1.73 લો.)
ઉત્તર:
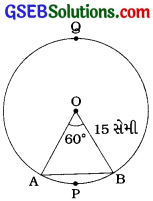
અહીં, વર્તુળની ત્રિજ્યા r = 15 સેમી અને જીવા AB કેન્દ્ર આગળ 60°નો ખૂણો આંતરે છે.
આથી લઘુવૃત્તાંશ OAPBનો ખૂણો θ = 60°.
લઘુવૃત્તાંશ OAPBનું ક્ષેત્રફળ =\(\frac{\theta}{360}\) × π r2
= \(\frac{\theta}{360}\) × 3.14 × 15 × 15 સેમી2
= 117.75 સેમી2
∆ OABમાં, ∠O = 60° અને OA = OB = 15 સેમી
∴ ∆ OAB એ સમબાજુ ત્રિકોણ છે. જેમાં દરેક બાજુની લંબાઈ a = 15 સેમી.
સમબાજુ ∆ OABનું ક્ષેત્રફળ
= \(\frac{\sqrt{3}}{4}\) a2
= \(\frac{1.73}{4}\) × 15 × 15 સેમી2
= 97.3125 સેમી2
વર્તુળનું ક્ષેત્રફળ = πr2
= 3.14 × 15 × 15 સેમી2
= 706.5 સેમી2
લઘુવૃત્તખંડ APBનું ક્ષેત્રફળ = લઘુવૃત્તાંશ OAPBનું ક્ષેત્રફળ – ∆ OABનું ક્ષેત્રફળ
= (117.75 – 97.3125) સેમી2
= 20.4375 સેમી2
ગુરુવૃત્તખંડ AQBનું ક્ષેત્રફળ = વર્તુળનું ક્ષેત્રફળ – લઘુવૃત્તખંડ APBનું ક્ષેત્રફળ
= (706.5 – 20.4375) સેમી2
= 686.0625 સેમી2
આમ, લઘુવૃત્તખંડનું ક્ષેત્રફળ 20.4375 સેમી2 અને ગુરવૃત્તખંડનું ક્ષેત્રફળ 686.0625 સેમી2 થાય.

પ્રશ્ન 7.
12 સેમી ત્રિજ્યાવાળા વર્તુળની જીવા કેન્દ્ર આગળ 120નો ખૂણો આંતરે છે. તેને અનુરૂપ વૃત્તખંડનું ક્ષેત્રફળ શોધો. (π = 3.14 અને √3 = 1.73 લો.)
ઉત્તર:
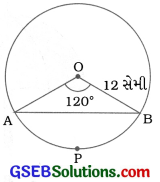
અહીં, વર્તુળની ત્રિજ્યા r = 12 સેમી અને લઘુવૃત્તાંશનો ખૂણો θ = 120°.
લઘુવૃત્તાંશ OAPBનું ક્ષેત્રફળ =\(\frac{\theta}{360}\) × 12
= \(\frac{120}{360}\) × 3.14 × 12 × 12 સેમી2
= 150.72 સેમી2
સમદ્વિબાજુ ∆ CABનું ક્ષેત્રફળ શોધવા માટે OM ⊥ AB દોરો.
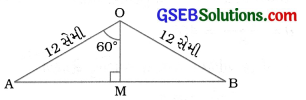
સમદ્વિબાજુ ત્રિકોણ OABમાં OA = OB હોવાથી, OM એ ∠AOBને તેમજ બાજુ ABને દુભાગે છે.
∠AOM = \(\frac{1}{2}\) ∠AOB = \(\frac{1}{2}\) × 120 = 60° અને AB = 2AM
∆ OMAમાં, ∠M = 90°
cos O = \(\frac{\mathrm{OM}}{\mathrm{OA}}\)
cos 60° = \(\frac{\mathrm{OM}}{12}\)
\(\frac{1}{2}=\frac{\mathrm{OM}}{12}\)
OM = 6 સેમી
અને sin O = \(\frac{\mathrm{AM}}{\mathrm{OA}}\)
sin 60° = \(\frac{\text { AM }}{12}\)
\(\frac{\sqrt{3}}{2}=\frac{\mathrm{AM}}{12}\)
AM = 6√3 સેમી
હવે, AB = 2AM = 2 × 6√3 = 12√3 સેમી
∆ DABનું ક્ષેત્રફળ = \(\frac{1}{2}\) × AB × OM
= \(\frac{1}{2}\) × 12√3 × 6 સેમી2
= 36 × 1.73 સેમી2
= 62.28 સેમી2
લઘુવૃત્તખંડ APBનું ક્ષેત્રફળ = લઘુવૃત્તાંશ OAPBનું ક્ષેત્રફળ – ∆ OABનું ક્ષેત્રફળ
= (150.72 – 62.28) સેમી2 = 88.44 સેમી2
આમ, અનુરૂપ વૃત્તખંડનું ક્ષેત્રફળ 88.44 સેમી2 છે.

પ્રશ્ન 8.
15 મી બાજુવાળા ચોરસ આકારના ઘાસના ખેતરના એક ખૂણે ઘોડાને 5 મી લાંબા દોરડાથી ખીલા સાથે બાંધેલો છે. (જુઓ આકૃતિ)

(i) ઘોડો ખેતરના જેટલા ભાગમાં ચરી શકે તેનું ક્ષેત્રફળ શોધો.
(ii) દોરડું 5 મીને બદલે 10 મી લાંબું રાખ્યું હોત, તો ચરવાના ક્ષેત્રફળમાં થતો વધારો શોધો. (π = 3.14 લો.)
ઉત્તર:
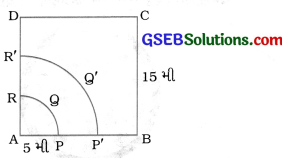
(i) અહીં, ABCD એ 15 મી બાજુવાળું ચોરસ ખેતર છે. જેના એક ખૂણે એટલે કે, શિરોબિંદુ A પર ઘોડાને 5 મી લાંબા દોરડાથી ખીલા સાથે બાંધેલો છે.
આથી ઘોડો લઘુવૃત્તાંશ APQR જેટલા ભાગમાં ચરી શકે. લઘુવૃત્તાંશ APQR માટે ત્રિજ્યા r = 5 મી (દોરડાની લંબાઈ) અને θ = 90° (ચોરસનો ખૂણો).
ઘોડો ખેતરના જેટલા ભાગમાં ચરી શકે તેનું ક્ષેત્રફળ = લઘુવૃત્તાંશ APQRનું ક્ષેત્રફળ
= \(\frac{\theta}{360}\) × π r2
= \(\frac{90}{360}\) × 3.14 × 5 × 5 મી2
= 19.625 મી2

(ii) જો દોરડું 10 મી લાંબુ રાખવામાં આવે, તો હવે ઘોડો લઘુવૃત્તાંશ AP’QR’ જેટલા ભાગમાં ચરી શકે. લઘુવૃત્તાંશ AP’Q’R’ માટે ત્રિજ્યા r = 10 મી અને θ = 90°. આ સંજોગોમાં ઘોડો ખેતરના જેટલા ભાગમાં ચરી શકે તેનું ક્ષેત્રફળ = લઘુવૃત્તાંશ AP’Q’R’ નું ક્ષેત્રફળ
= \(\frac{\theta}{360}\) × π r2
= \(\frac{90}{360}\) × 3.14 × 10 × 10 મી2
= 78.5 મી2
આથી ચરવાના ક્ષેત્રફળમાં થતો વધારો = (78.5 – 19.625) મી2 = 58.875 મી2
આમ, મૂળ પરિસ્થિતિ, એટલે કે દોરડાની લંબાઈ 5 મી હોય, તો ઘોડો ખેતરમાં 19.625 મી2 વિસ્તારમાં ચરી શકે અને જો દોરડાની લંબાઈ 10 મી કરવામાં આવે, તો ઘોડો ચરી શકે તે વિસ્તારના ક્ષેત્રફળમાં 58.875 મી2 શ્નો વધારો થાય.

પ્રશ્ન 9.
ચાંદીના તારથી 35 મિમી વ્યાસવાળું વર્તુળ આકારનું એક બક્કલ જેવું ઘરેણું બનાવ્યું છે. આપેલ આકૃતિમાં બતાવ્યા પ્રમાણે વર્તુળને 10 સમાન વૃત્તાંશમાં વિભાજિત કરે તેવા 5 વ્યાસ બનાવવામાં પણ તારનો ઉપયોગ કર્યો છે.
(i) જરૂરી ચાંદીના તારની કુલ લંબાઈ શોધો.
(ii) ઘરેણાના દરેક વૃત્તાંશનું ક્ષેત્રફળ શોધો.
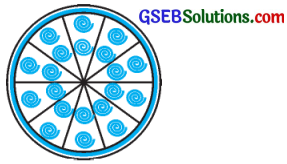
ઉત્તર:
આપેલ બક્કલ જેવા ઘરેણાનો વ્યાસ d = 35 મિમી હોવાથી ત્રિજ્યા r = \(\frac{35}{2}\) મિમી
(i) જરૂરી ચાંદીના તારની કુલ લંબાઈ પરિઘ અને પાંચ વ્યાસના સરવાળા દ્વારા મળે. જરૂરી ચાંદીના તારની કુલ લંબાઈ = πd + 5d
= (\(\frac{22}{7}\) × 35 + 5 × 35) મિમી
= (110 + 175) મિમી
= 285 મિમી
(ii) વર્તુળને 10 સમાન વૃત્તાંશમાં વિભાજિત કરવામાં આવ્યું છે.
માટે, 10 સમાન વૃત્તાંગ પૈકી દરેક વૃત્તાંશ માટે ત્રિજ્યા r = \(\frac{35}{2}\) મિમી અને θ = \(\frac{360}{10}\) = 36°.
દરેક લઘુવૃત્તાંશનું ક્ષેત્રફળ = \(\frac{\theta}{360}\) × π r2
= \(\frac{36}{360} \times \frac{22}{7} \times \frac{35}{2} \times \frac{35}{2}\) મિમી2
=\(\frac{385}{4}\) મિની2
આમ, જરૂરી તારની કુલ લંબાઈ 285 મિમી થાય અને દરેક વૃત્તાંશનું ક્ષેત્રફળ \(\frac{385}{4}\) મિમી2 થાય.

પ્રશ્ન 10.
એક છત્રીમાં સમાન અંતરે 8 સળિયા આવેલા છે. (જુઓ આકૃતિ) છત્રીને 45 સેમી ત્રિજ્યાવાળું સમતલીય વર્તુળ ધારી, છત્રીના બે ક્રમિક સળિયા વચ્ચેના ભાગનું ક્ષેત્રફળ શોધો.
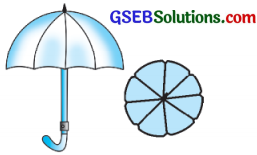
ઉત્તર:
છત્રીના બે ક્રમિક સળિયા વચ્ચેનું ક્ષેત્રફળ એવા લઘુવૃત્તાંશના ક્ષેત્રફળ દ્વારા મળે, જે લઘુવૃત્તાંશ માટે ત્રિજ્યા r = 45 સેમી અને θ = \(\frac{360^{\circ}}{8}\) = 45°.
બે ક્રમિક સળિયા વચ્ચેના ભાગનું ક્ષેત્રફળ = લઘુવૃત્તાંશનું ક્ષેત્રફળ
= \(\frac{\theta}{360}\) × π r2
= \(\frac{45}{360} \times \frac{22}{7}\) × 45 × 45 સેમી2
= \(\frac{22275}{28}\) સેમી2
આમ, છત્રીના બે ક્રમિક સળિયા વચ્ચેના ભાગનું ક્ષેત્રફળ \(\frac{22275}{28}\) સેમી2 થાય.

પ્રશ્ન 11.
એક ગાડીને એકબીજા પર આચ્છાદિત ન થાય તેવાં બે વાઇપર છે. દરેક વાઇપરને 115° ના ખૂણા જેટલી સફાઈ કરતી 25 સેમી લંબાઈની બ્લેડ છે. પ્રત્યેક વખતે વાઇપરથી સાફ થતા વિસ્તારનું કુલ ક્ષેત્રફળ શોધો.
ઉત્તર:
પ્રત્યેક વખતે વાઈપરથી સાફ થતા વિસ્તારનું ક્ષેત્રફળ બે લઘુવૃત્તાંશના કુલ ક્ષેત્રફળ જેટલું થાય.
અહીં, દરેક લઘુવૃત્તાંશ માટે ત્રિજ્યા r = 25 સેમી (વાઇપરની લંબાઈ) અને θ = 115°.
પ્રત્યેક વખતે વાઇપરથી સાફ થતા વિસ્તારનું કુલ ક્ષેત્રફળ = 2 × લઘુવૃત્તાંશનું ક્ષેત્રફળ
= 2 × \(\frac{\theta}{360}\) × π r2
= 2 × \(\frac{115}{360} \times \frac{22}{7}\) × 25 × 25 સેમી2
= \(\frac{158125}{126}\) સેમી2
આમ, પ્રત્યેક વખતે વાઇપરથી સાફ થતા વિસ્તારનું કુલ ક્ષેત્રફળ 158125 સેમી2 થાય.

પ્રશ્ન 12.
પાણીની નીચેના ખડકો વિશે જહાજને ચેતવણી આપવા માટે, એક દીવાદાંડી 16.5 કિમી અંતર સુધી 80° વૃત્તાંશના ખૂણે લાલ રંગનો પ્રકાશ પાથરે છે. સમુદ્રના જેટલા ક્ષેત્રફળ પર જહાજને ચેતવણી અપાતી હોય તે શોધો. (π = 3.14 લો.)
ઉત્તર:
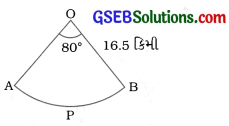
લાલ રંગનો પ્રકાશ લઘુવૃત્તાંશ OAPB વિસ્તારમાં પથરાય છે.
લઘુવૃત્તાંશ OAPB માટે, ત્રિજ્યા r = 16.5 કિમી અને θ = 80°.
સમુદ્રના જેટલા વિસ્તાર પર જહાજને ચેતવણી અપાતી હોય તેનું ક્ષેત્રફળ = લઘુવૃત્તાંશ OAPBનું ક્ષેત્રફળ
= \(\frac{\theta}{360}\) × π r2
= \(\frac{80}{360}\) × 3.14 × 16.5 × 16.5 કિમી2
= 189.97 કિમી2
આમ, સમુદ્રના 189.97 કિમી2 વિસ્તારમાં જહાજને ચેતવણી અપાય છે.

પ્રશ્ન 13.
આપેલ આકૃતિમાં બતાવ્યા પ્રમાણે એક વર્તુળાકાર મેજ પર છે ભાતવાળું એક આવરણ પાથરેલું છે. જો આવરણની ત્રિજ્યા 28 સેમી હોય, તો ₹ 0.35 પ્રતિ સેમી2 ના દરે ડિઝાઇન બનાવવાનો ખર્ચ શોધો. (√3 = 1.7 લો.).
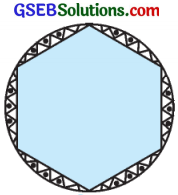
ઉત્તર:
વર્તુળાકાર આવરણ માટે ત્રિજ્યા r = 88 સેમી.
વર્તુળાકાર આવરણનું ક્ષેત્રફળ = π r2
= \(\frac{22}{7}\) × 28 × 28 સેમી2
= 2464 સેમી2
વર્તુળાકાર આવરણના જેટલા ભાગમાં ડિઝાઇન નથી તે છે સમબાજુ ત્રિકોણ દ્વારા બનતો નિયમિત ષટ્કોણ છે. દરેક સમબાજુ ત્રિકોણની બાજુનું માપ a = 28 સેમી (ત્રિજ્યા).
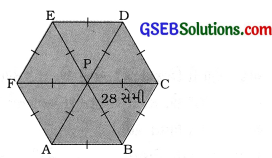
નિયમિત ષટ્કોણ ABCDEFનું ક્ષેત્રફળ = 6 × સમબાજુ ત્રિકોણ PABનું ક્ષેત્રફળ
= 6 × \(\frac{\sqrt{3}}{4}\) a2
= 6 × \(\frac{1.7}{4}\) × 28 × 28 સેમી2
= 1999.2 સેમી2
જે પ્રદેશમાં ડિઝાઇન કરેલ છે તે પ્રદેશનું ક્ષેત્રફળ = વર્તુળનું ક્ષેત્રફળ – નિયમિત ષટ્કોણ ABCDEFનું ક્ષેત્રફળ
= (2464 – 1999.2) સેમી2
= 464.8 સેમી2
1 સેમી2 વિસ્તારમાં ડિઝાઇન બનાવવાનો ખર્ચ = ₹ 0.35
∴ 464.8 સેમી, વિસ્તારમાં ડિઝાઇન બનાવવાનો ખર્ચ
= ₹ (464.8 × 0.35) = ₹ 162.68
આમ, ડિઝાઇન બનાવવાનો ખર્ચ ₹ 162.68 થાય.

પ્રશ્ન 14.
નીચેનામાં સાચા જવાબ આગળ નિશાની કરોઃ
R ત્રિજ્યાવાળા વર્તુળનો વૃત્તાંશ ખૂણો p° હોય, તો વૃત્તાંશનું ક્ષેત્રફળ ………… થાય.
(A) \(\frac{P}{180}\) × 2πR
(B) \(\frac{P}{180}\) × πR2
(C) \(\frac{P}{360}\) × 2πR
(D) \(\frac{P}{720}\) × 2πR2
ઉત્તર:
આપેલ વૃત્તાંશ માટે ત્રિજ્યા r = R અને વૃત્તાંશનો ખૂણો θ = p.
વૃત્તાંશનું ક્ષેત્રફળ = \(\frac{\theta}{360}\) × πR2
= \(\frac{P}{180}\) × πR2
= \(\frac{P}{720}\) × 2πR2
આમ, સાચો વિકલ્પ (D) \(\frac{P}{720}\) × 2πR2 છે.