Gujarat Board GSEB Solutions Class 10 Maths Chapter 12 Areas Related to Circles Ex 12.3 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 10 Maths Chapter 12 Areas Related to Circles Ex 12.3
Question 1.
Find the area of shaded region in the given figure. If PQ = 24 cm, PR = 7 cm, and O is the centre of the circle. (CBSE 2012)
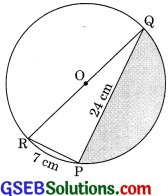
Solution:
∠QPR is right angle (Angle subtended in semicircle is right angle)
Therefore
QR2 = PR2 + PQ2 = 242 + 72 = 576 + 49
QR2 = 625
QR = 25 cm
r = \(\frac {25}{2}\) cm
Hence, area of shaded region
= Area of semicircle – Area of ΔPQR
= \(\frac {1}{2}\) πr2 – \(\frac {1}{2}\) x PQ x PR
= \(\frac {1}{2}\) x \(\frac {22}{7}\) x \(\frac {25}{2}\) x \(\frac {25}{2}\) – \(\frac {1}{2}\) x 24 x 7
= \(\frac {6875}{28}\) – 84 = \(\frac {6875 – 84 × 28}{28}\) = \(\frac {4523}{28}\) cm2
Hence, area of shaded region is cm2.
![]()
Question 2.
Find the area of the shaded region in given figure, if radii of the two concentric circles with centre O are 7 cm and 14 cm respectively and
∠AOC = 40°. (CBSE 2012)
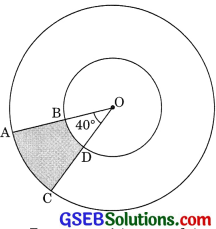
Solution:
Here r1 = 7 cm, r1 = 14 cm and θ = 40°
Area of shaded region
= \(\frac{\pi r_{2}^{2} \theta}{360^{\circ}}\) – \(\frac{\pi r_{1}^{2} \theta}{360^{\circ}}\) = \(\frac{\pi \theta}{360^{\circ}}\) = [r22 – r12
= \(\frac{\frac{22}{7} \times 40^{\circ}}{360^{\circ}}\) [142 – 72]
= \(\frac{22 \times 40}{7 \times 360}\) [196 – 49]
= \(\frac{22}{7 \times 9}\) x 147 = \(\frac{22}{9}\) x 21 = \(\frac{154}{3}\) cm2
Question 3.
Find the area of shaded region in the given figure, if ABCD is a square of side 14 cm and APD and BPC are semicircies.
Solution:
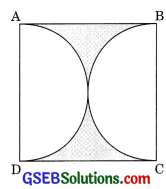
Side of square = 14 cm
Radius of semicircle = \(\frac{14}{2}\) = 7 cm
Area of shaded region
= Area of square – 2 x area of semicircle
= Side x Sue – 2 x πr2 = 14 x 14 – πr2
= 196 – \(\frac{22}{7}\) x 7 x 7
= 196 – 154 = 42 cm2
![]()
Question 4.
Find the area of the shaded region in the given figure, where a circular arc of radius 6 cm has been drawn with vertex O of an equilateral triangle OAB of side 12 cm as centre. (CBSE 2016)
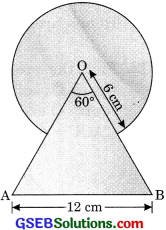
Solution:
Here r = 6 cm
ΔAOB is an equilateral triangle.
Hence θ = 60°
Area of shaded region
= Area of an equilateral triangie + Area of circle – Area of sector

Question 5.
From each corner of a square of side 4 cm a quadrant of a circle of radius 1 cm is cut and also a circle of diameter 2 cm is cut as shown in figure. Find the area of the remaining portion of the square.
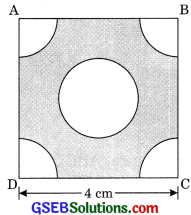
Solution:
Radius of circle = \(\frac{2}{1}\) = 1 cm
Radius of quadrant = 1 cm
Area of shaded region
= Area of square – (Area of 4 quadrants + Area of circle)
= 4 x 4 -[ 4 x \(\frac{1}{4}\)πr2 + πr2]
= 16 – 2πr2
= 16 – 2 x \(\frac{22}{7}\) x 12 = 16 – \(\frac{44}{7}\)
= \(\frac{112 – 44}{7}\) = \(\frac{68}{7}\) cm2
![]()
Question 6.
In a circular table cover of radius 32 cm, a design is formed leaving an equilateral triangle ABC in the middle as shown in figure. Find the area of the design (Shaded region).
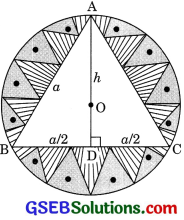
Solution:
ABC is an equilateral triangle.
Centre of circle coincide the centroid of the equilateral triangle.
Hence, = \(\frac{OD}{OA}\) = \(\frac{1}{2}\)
\(\frac{OD + OA }{OA}\) = \(\frac{3}{2}\)
\(\frac{h}{r}\) = \(\frac{3}{2}\)
h = 32 x \(\frac{3}{2}\) = 48 cm
Now in ft. ADB
AB2 = AD2 + BD2
⇒ a2 = 482 + (\(\frac{a}{2}\))2
⇒ a2 – \(\frac{a^{2}}{4}\) = 48 x 48
⇒ \(\frac{3a^{2}}{4}\) = 48 x 48
⇒ a2 = \(\frac{48 \times 48 \times 4}{3}\)
⇒ a2 = 64 x 48
Area of design or shaded region
= πr2 – \(\frac{\sqrt{3}}{4}\) x 64 x 48
= \(\frac{22}{7}\) x 32 x 32 – 16 x 48 \(\sqrt{3}\)
= (\(\frac{22528}{7}\) – 768\(\sqrt{3}\)) cm2
![]()
Question 7.
In figure, ABCD is a square of side 14 cm with centres A, B, C and D, four circles are drawn such that each circle touch externally two of the remaining three circles. Find the area of shaded region.
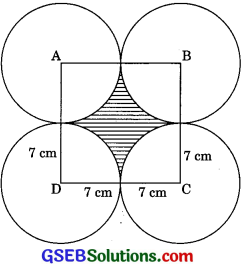
Solution:
Side of square = 14 cm
Radius of square = 7 cm
Area of shaded region
= Area of square – 4 x Area of quadrants
= Side x Side – 4 x \(\frac{1}{4}\) πr2
= 14 x 14 – x \(\frac{22}{7}\) x 72
= 196 – 22 x 7 = 196 – 154 = 42 cm2
![]()
Question 8.
Figure depicts a racing track whose left and right ends are semicircular. The distance between the two inner parallel line segments is 60 m and they are each 106 m long. If the track is 10 m wide, find:
(i) the distance around the track along its inner edge.
(ii) the area of the track.

Solution:
(i) Distance between two inner parallel lines = 60 m
Radius of inner circular ends = \(\frac{60}{2}\) = 30m
The distance around the track along its inner track
= 106 + 106 + 2 x circumference of semicircle
= 212 + 2 x \(\frac{1}{2}\) x 2πr
= 212 + 2 x \(\frac{22}{7}\) x 30 = 212 + \(\frac{1320}{7}\)
= \(\frac{1484 + 1320}{7}\) = \(\frac{2804}{7}\) m
(ii) Area of the track
= Area of two rectangular track
+ 2 x [\(\frac{1}{2}\) πr22 – \(\frac{1}{2}\)r21]
= 2 x 106 x 10 + 2 x \(\frac{1}{2}\)π[(30 + 10)2 – (30)2]
= 2120 + \(\frac{22}{7}\) [402 – 302]
= 2120 + \(\frac{22}{7}\) x (40 + 30) x (40 – 30)
= 2120 + \(\frac{22}{7}\) x 70 x 10
= 2120 + 2200
= 4320 m2
![]()
Question 9.
In figure, AB and CD are two diameters of a circle (with centre O) perpendicular to each other and OD is the diameter of the smaller circle. If OA = 7 cm, find the area of the shaded region. (CBSE 2000, 2010, 2013)
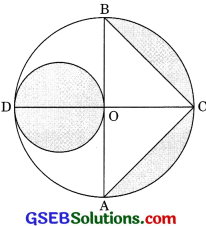
Solution:
Here, OA is the radius of larger circle, i.e.,
r = 7 cm
AB = 2r = 2 x 7 = 14cm
Radius of smaller circle,
r2 = \(\frac{OD}{2}\) = \(\frac{7}{2}\) cm
Area of shaded region = Area of smaller circle + Area of semicircle – Area of ΔABC
= πr22 + (\(\frac{1}{2}\)πr2 – \(\frac{1}{2}\) x AB x OC)
= π x (\(\frac{7}{2}\))2 + \(\frac{1}{2}\)π x 72 – \(\frac{1}{2}\) x 14 x 7
= \(\frac{49π}{4}\) + \(\frac{49π}{2}\) – 49 = \(\frac{147 π}{4}\) – 49
= \(\frac{147 – 22}{4 x 7}\) – 49 = \(\frac{21 x 11}{2}\) – 49
= \(\frac{231 – 98}{2}\) = \(\frac{133}{4 x 7}\) = 66.5 cm2
![]()
Question 10.
The area of an equilateral triangle ABC is 17320.5 cm2. With each vertex of the triangle as centre, a circle is dräwn with radius equal to half the length of side of the triangle (see figure). Find the area of shaded region. (Use π = 3.14 and \(\sqrt{3}\) = 1.73205)
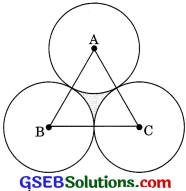
Solution:
Hence, area of an equilateral triangle
= \(\frac{\sqrt{3}}{4}\) a2
\(\frac{\sqrt{3}}{4}\)a2 = 17320.5
⇒ a2 = \(\frac{17320.5 \times 4}{\sqrt{3}}\)
⇒ a2 = \(\frac{17320.5 \times 4}{\sqrt{3}}\)
a2 = \(\frac{17320.5 \times 4}{1.73205}\)
a2 = 40,000
a2 = 200 cm
Radius of circle = \(\frac{200}{2}\) = 100 cm
Area of shaded region = Area of an equilateral triangle – 3 x Area of sectors
= 17320.5 – 3 x \(\frac{\pi r^{2} \theta}{360^{\circ}}\)
= 17320.5 – 3 x \(\frac{3.14 \times 100^{2} \times 60^{\circ}}{360^{\circ}}\)
= 17320.5 – 3 x \(\frac{3.14 \times 10000}{6}\)
= 17320.5 – 15700 = 1620.5 cm2
![]()
Question 11.
On a square handkerchief, nine circular designs each of radius 7 cm are made (see figure). Find the area of the remaining portion of the handkerchief.
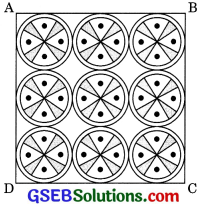
Solution:
Here, side of square ABCD
= 3 x diameter of a circular design
= 3 x d = 3 x 2r
= 6 x 7 = 42cm
Area of remaining handkerchief = Area of square ABCD – Area of 9 circular designs
= Side x Side – 9πr2
= 42 x 42 – 9 x \(\frac{22}{7}\) x 7 x 7
= 1764 – 9 x 22 x 7 = 1764 – 1386
= 378 cm2
![]()
Question 12.
In figure OACB is a quadrants of circle with centre O and radius 3.5 cm. If OD = 2 cm, find the area of the
(i) quadrant OACB
(ii) shaded region. (CBSE 2017)
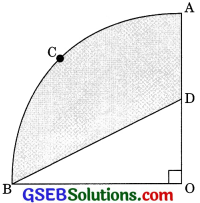
Solution:
(i) Area of quadrant AOBC
\(\frac{1}{4}\)πr2 = \(\frac{1}{4}\) x \(\frac{22}{7}\) x 3.52
= \(\frac{1}{4}\) x \(\frac{22}{7}\) = \(\frac{35}{10}\) x \(\frac{35}{10}\) = \(\frac{77}{8}\)cm2
(ii) Area of shaded region = Area of the quadrant OACB – area of the ΔOBD
= \(\frac{77}{8}\) – \(\frac{1}{2}\) OB x OD
= \(\frac{77}{8}\) – \(\frac{1}{2}\) x 3.5 x 2 = \(\frac{77}{8}\) – \(\frac{35}{10}\)
= \(\frac{77}{8}\) – \(\frac{7}{2}\) = \(\frac{77 – 28}{8}\) = \(\frac{49}{8}\) cm2
Question 13.
In figure, a square OABC is inscribed in a quadrant OPBQ If OA = 20 cm, find the area of the shaded region.
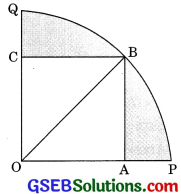
(Use π = 3.14) (CBSE 2012, 2014)
Solution:
In rt. ΔOAB
OB2 = OA2 + AB2
OB2 = 202 + 202
OB2 = 400 + 400
OB = 20\(\sqrt{2}\) cm
r = OB = 20\(\sqrt{2}\) cm
Area of shaded region = Area of quadrant – Area of square OABC
= \(\frac{1}{4}\)πr2 – OA x OA
= \(\frac{1}{4}\) x 3.14 x (20\(\sqrt{2}\))2 – 20 x 20
= \(\frac{1}{4}\) x 3.14 x 20 x 20 x 2 – 400
= 628 – 400 = 228 cm2
![]()
Question 14.
AB and CD are respectively arcs of two concentric circles of radii 21 cm and 7 cm and centre O (see figure). If ∠AOB = 30°, find the area of shaded region.
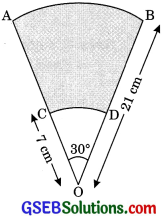
Solution:
Here r1 = 7 cm
r2 = 21 cm
and θ = 30°
Area of shaded region = Area of shaded region OAB – Area of shaded region OCD

Question 15.
In figure, ABC is a quadrant of a circle of radius 14 cm and a semicircle is drawn with BC as diameter. Find the area of shaded region. (CBSE 2008,2012)
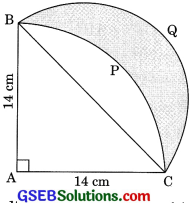
Solution:
Here, radius of quadrant, r = 14 cm
In rt. ΔBAC
BC2 = AB2 + BC2
BC2 = 142 + 142
= 196 + 196
BC2 = 2 x 196
BC = \(\sqrt{196 \times 2}\)
BC = 14\(\sqrt{2}\) cm
r1 = \(\frac{14 \sqrt{2}}{2}\) = 7 \(\sqrt{2}\) cm
Area of segment BCPB = Area of quadrant ACPB – Area of ΔABC
= \(\frac{1}{4}\)πr2 – \(\frac{1}{2}\)AC x AB
= \(\frac{1}{4}\) x \(\frac{22}{7}\) x 142 – \(\frac{22}{7}\) – 14 x 14
= \(\frac{22}{4 x 7}\) x 14 x 14 – 98
= 154 – 98 = 56 cm2
Area of shaded region = Area of semicircle – Area of segment BCPB
= \(\frac{1}{2}\) πr22 – 56
= \(\frac{1}{2}\) x \(\frac{22}{7}\) x (7\(\sqrt{2}\))2 -56
= \(\frac{11}{7}\) x 49 x 2 – 56
= 154 – 56 = 98 cm2
![]()
Question 16.
Calculate the area of the diagonal region in figure common between the two quadrants of circles of radius 8 cm each.
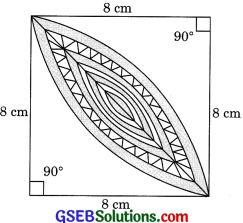
Solution:
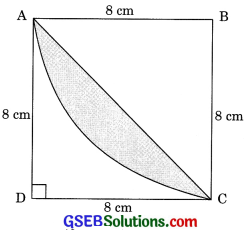
Area of segment
= Area of sector – Area of ΔABC

Area of shaded region = 2 x \(\frac{128}{7}\) = \(\frac{256}{7}\) cm2
![]()